During my 2017 binge of LW, I recall Yudkowsky suggesting that a superintelligence could infer the laws of physics from a single frame of video showing a falling apple (Newton apparently came up with his idea of gravity from observing a falling apple).
I now think that's somewhere between deeply magical and utter nonsense.
Interesting! My intuition says roughly the opposite -- "be able to infer the laws of physics from a single frame of video showing an apple" seems to be barely superhuman to me. I would expect the first few steps to be achievable by a smart-but-not-exceptionally-smart and mathematically inclined programmer with a decently powerful computer, given enough time, and more specifically would look like.
- Determine the format of the video (easy for a human if not compressed, probably still possible for a computer-assisted human if compressed with something around the complexity level of gzip)
- See that the format describes something like a grid of cells, where each cell has three [something] values.
- Come up with the hypothesis that the grid represents a 2d projection of a 3d space (this does not feel like a large jump to me given that ray tracers exist and are not complicated, but I can go into more detail on this step if you'd like).
- From the presence of chromatic aberration, determine that the three channels represent intensities of the same thing at different levels (from here on out I'll say "intensity of light at different frequencies" because talking of "things" is not that useful, but at this stage I'd expect their model to be something along the lines of "this grid was generated by something like a ray tracer with these particular shapes at these points, a light source over here")
- Determine the shape of the lens by looking at edges and how they are distorted.
- If the apple is out in sunlight, I expect that between the three RGB channels and the rainbows generated by chromatic aberration would be sufficient to determine that the intensity-by-frequency of light approximately matches the blackbody radiation curves (though again, not so much with that name as just "these equations seem to be a good fit")..
From there, I think the next bits of evidence would have to do with the particulars of the sensors used, e.g.
- If they're sensitive enough that the observer can pick up emission lines of hydrogen from the sun and absorption lines from the atmosphere, I expect those would be informative and suggest some sort of simple mathematical model
- If there are any shutter artifacts, that's probably enough to build a model of "things are moving over time".
- Any post-processing of the image probably leaves signs
Whether or not that's enough to reconstruct all physical laws seems to me to depend mostly on whether it's possible to go from understanding optic + enough QM to explain emission spectra to a complete understanding of the physical laws underlying our universe, or whether you end up with something that looks more like newtonian mechanics.
It's not that it's magic, it's that a single image taken of the physical world with modern physical sensors contains a lot of information about the physical world. I expect that a superintellegent AI would be able to pick up a lot more information from a picture of a physical apple falling than it would from a video generated by raytracing a scene in which an apple falls.
This response is totally absurd. Your human priors are doing an insane amount of work here - you're generating an argument for the conclusion, not figuring out how you would privilege those hypotheses in the first place.
See that the format describes something like a grid of cells, where each cell has three [something] values.
This seems maybe possible for png (though it could be hard - the pixel data will likely be stored as a single contiguous array, not a bunch of individual rows, and it will be run-length encoded, which you might be able to figure out but very well might not - and if it's jpg compressed this is even further from the truth).
Come up with the hypothesis that the grid represents a 2d projection of a 3d space (this does not feel like a large jump to me given that ray tracers exist and are not complicated, but I can go into more detail on this step if you’d like).
It's a single frame, you're not supposed to have seen physics before. How did ray tracers enter into this? How do you know your world is 3D, not actually 2D? Where is the hypothesis that it's a projection coming from, other than assuming your conclusion?
Determine the shape of the lens by looking at edges and how they are distorted.
How do you know what the shapes of the edges should be?
If the apple is out in sunlight, I expect that between the three RGB channels and the rainbows generated by chromatic aberration would be sufficient to determine that the intensity-by-frequency of light approximately matches the blackbody radiation curves (though again, not so much with that name as just “these equations seem to be a good fit”)..
What's "sunlight"? What's "blackbody radiation"? How would a single array of numbers of unknown provenance without any other context cause you to invent these concepts?
This seems maybe possible for png (though it could be hard - the pixel data will likely be stored as a single contiguous array, not a bunch of individual rows, and it will be run-length encoded, which you might be able to figure out but very well might not - and if it's jpg compressed this is even further from the truth).
I mean, once you've got your single continuous array it's pretty easy to notice "hey this pattern almost repeats every 1080 triplets". Getting from the raw data stream to your single continuous array might be very simple (if your video format is an uncompressed "read off the RGB values left-to-right, top-to-bottom, frame-by-frame"), fairly simple ("sequence of pngs"), fairly complex but probably still within the first million guesses a mathy human with a computer and an unbounded attention span might make ("sequence of jpgs"), or possibly harder than all the other parts combined if it's H.264 or something like that, or probably impossibly no matter how good the superintelligence is if you hand it an sequence of bitmaps encrypted with a 1024 bit key or something like that.
It's a single frame, you're not supposed to have seen physics before. How did ray tracers enter into this?
You don't need physics to build a ray tracer. You need geometry and linear algebra, which is why I specified that it was a mathematically inclined programmer. Have a look at this raytracer implementation in 35 lines of Javascript, and note how there's lots of stuff about defining what the dot product of a vector is and how to compute the intersection between a ray and a sphere, and no stuff about atoms or molecules or quantum mechanics.
Where is the hypothesis that it's a projection coming from, other than assuming your conclusion?
Trying a bunch of different hypotheses and seeing which one fits best.
"This 2-d grid was generated by taking a point and a plane in a higher-dimensional space, drawing a grid on that plane, and then generating a line from that point to each grid intersection on that plane, and then [doing something with] those rays and a small number of simple geometric shapes in that space" seems like a pretty obvious hypothesis to me. If it doesn't seem like one of the first million hypotheses a mathematically inclined alien that lived in a universe that operated on different rules would come up with, I don't know what to tell you. And "reflect off at the same angle as the angle of incidence" is I'd guess among the hundred simplest [doing something with] you can do with a ray and a shape.
I imagine "a sphere that reflects mostly red at (x=0,y=0,z=+1,r=1/16), a plane that emits on the green channel at (y=-1), another plane that emits mainly on the blue channel at (y=+1), and a sphere that strongly emits approximately the same on each channel at (x=-1/2,y=1,z=-1/2)" would describe a scene with a red apple falling onto a green lawn under a sunny blue sky surprisingly well for the length of program needed to encode it, probably much better than "a blue rectangle, a green rectangle, and a red circle on a 2-d plane and also the red circle has this particular complicated shading pattern" per bit.
Before I go any further with this explanation, can you enumerate where, if anywhere, you disagree with a human-level but extremely alien intelligence with a computer, unlimited patience, and lots of time being able to eventually do the following
- When receiving a definitely nonrandom signal, hypothesize that signal was probably generated by some process which it is possible to model
- Hypothesize that a one-dimensional array of 1,572,864 bytes that nearly repeats every 3 bytes, and which nearly repeats every 1,024 triplets, might represent a 1024 x 512 x 3 grid of something
- Observe that the triplets, have correlated but not perfectly correlated values which are more tightly correlated for nearby (on the other two axes) triplets than faraway ones. Hypothesize that they might represent measures of similar things on three different channels
- Some simple short program might be able to generate a grid which looks somewhat like that grid
- A ray traced scene or similar, being rather simple, is one of the programs the alien will eventually try
- Once the alien has the idea of a ray-traced scene, they can tinker with adding / removing / moving / changing the other properties of shapes in the scene to make it more clearly fit the grid it received
- The alien will be able to get quite close to the original scene by doing this for long enough.
- There will come a point where tinkering with the properties of the objects in the scene does not actually allow the alien to improve the model more.
- That point will come much later for the "ray tracing a scene in 3d space" model than the "paint a picture in 2d space" model, implying that the "ray tracing in 3d space" is a better model
- At the time this happens, the difference between the scene the alien generates and the actual photo will still show some sort of regular structure, implying that "a ray-traced 3d scene" does not fully describe the process that generated the original grid.
Alternatively, is your hypothesis that said alien might be able to do each of these steps individually, but would eventually get stuck due to the combinatorial explosion in the number of different combinations of things to try?
The issue is there’s no feedback during any of this other than “does this model succinctly explain the properties of this dataset?” It’s pure Occam’s Razor, with nothing else. I would suspect that there are far simpler hypothesis than the entirety of modern physics which would predict the output. I’m going to walk through if I was such an alien as you describe, and see where I end up (I predict it will be different from the real world, but will try not to force anything).
"Pure Occam's Razor" is roughly how I would describe it too. I suspect the difference in our mental models is one of "how far can Occam's Razor take you?". My suspicion is that "how well you can predict the next bit in a stream of data" and "how well you understand a stream of data" are, in most¹ cases, the same thing.
In terms of concrete predictions, I'd expect that if we
- Had someone² generate a description of a physical scene in a universe that runs on different laws than ours, recorded by sensors that use a different modality than we use
- Had someone code up a simulation of what sensor data with a small amount of noise would look like in that scenario and dump it out to a file
- Created a substantial prize structured mostly³ like the Hutter Prize for compressed file + decompressor
we would see that the winning programs would look more like "generate a model and use that model and a similar rendering process to what was used to original file, plus an error correction table" and less like a general-purpose compressor⁴.
¹ But I probably wouldn't go so far as to say "all" -- if you handed me a stream of bits corresponding to concat(sha1(concat(secret, "1")), sha1(concat(secret, "2")), sha1(concat(secret, "3")), ...sha1(concat(secret, "999999"))), and I knew everything about the process of how you generated that stream of bits except what the value of secret was, I would say that I have a nonzero amount of understanding of that stream of bits despite having zero ability to predict the next bit in the sequence given all previous bits.
² Maybe Greg Egan, he seems to be pretty good at the "what would it be like to live in a universe with different underlying physics" thing
³ Ideally minus the bit about the compression and decompression algos having to work with such limited resources
⁴ Though I will note that, counter to my expectation here, as far as I know modern lossless photo compression does not look like "build a simulation of some objects in space, fine tune, and apply a correction layer" despite this being what my model of the world predicting humanity would create in a world where computation is cheap and bandwidth is expensive.
Edit: formatting
If I gave you a random binary file with no file extension and no metadata, how confident are you that you can tell me the entire provenance of that information?
Extremely confident you could construct a file such that I could not even start giving you the provenance of that information. Trivially, you could do something like "aes256 encrypt a 2^20 bytes of zeros with the passphrase ec738958c3e7c2eeb3b4".
My contention is not so much "intelligence is extremely powerful" as it is "an image taken by a modern camera contains a surprisingly large amount of easy-to-decode information about the world, in the information-theoretic sense of the word information".
If you were to give me a binary file with no extension and no metadata that is
- Above 1,000,000 bytes in size
- Able to be compressed to under 50% of its uncompressed size with some simple tool like
gzip(to ensure that there is actually some discoverable structure) - Not able to be compressed under 10% of its uncompressed size by any well-known existing tools (to ensure that there is actually a meaningful amount of information in the file)
- Not generated by some tricky gotcha process (e.g. a file that is 250,000 bytes from
/dev/randomfollowed by 750,000 bytes from/dev/zero)
then I'd expect that
- It would be possible for me, given some time to examine the data, create a decompressor and a payload such that running the decompressor on the payload yields the original file, and the decompressor program + the payload have a total size of less than the original gzipped file
- The decompressor would legibly contain a substantial amount of information about the structure of the data.
I would not expect that I would be able to tell you the entire provenance of the information, even if it were possible in principle to deduce from the file, since I am not a superintelligence or even particularly smart by human standards.
I notice that this is actually something that could be empirically tested -- if you wanted we could actually run this experiment at some point (I anticipate being pretty busy for the next few weeks, but on the weekend of July 16/17 I will be tied to my computer for the duration of the weekend (on-call for work), so if you have significantly different expectations about what would happen, and want to actually run this experiment, that would be a good time to do it for me.
P.S. A lot of my expectations here come from the Hutter Prize, a substantial cash prize for generating good compressions of the first gigabyte of Wikipedia. The hypothesis behind the prize is that, in order to compress data, it is helpful to understand that data. The current highest-performing algorithm does not have source code available, but one of the best runner-ups that actually gives source code works using a process that looks like
The transform done by paq8hp1 through paq8hp5 is based on WRT by Przemyslaw Skibinski, which first appeared in PAsQDa and paqar, and later in paq8g and xml-wrt. The steps are as follows:
- The input is parsed into seqences of all uppercase letters or all lowercase letters, or one uppercase letter followed by lowercase letters, e.g. "THE", "the", or "The".
- All uppercase words are prefixed by a special symbol (0E hex in paq8hp3, paq8hp4, paq8hp5). If a lowercase letter follows with no intervening characters (e.g. "THEre", then a special symbol (0C hex) marks the end. (e.g. 0E "the" 0C "re").
- Capitalized words are prefixed with 7F hex (paq8hp3) or 40 hex (paq8hp4, paq8hp5) (e.g. "The" -> 40 "the").
- All letters are converted to lower case.
- Words are looked up in the dictionary. The first 80 words in the dictionary are coded with 1 byte: 80, 81, ... CF (hex).
- The next 2560 words (paq8hp1-4) or 3840 words (paq8hp5) are coded with 2 bytes: D080, D081, ... EFCF (paq8hp1-4), or D080, ... FFCF (paq8hp5).
- The last 40960 words are coded with 3 bytes: F0D080, F0D081, ... FFEFCF.
- If a word does not match, then the longest matching prefix with length at least 6 is coded and the rest of the word is spelled.
- If there is no matching prefix, then the longest matching suffix with length at least 6 is coded after spelling the preceding letters.
- If no matching word, prefix, or suffix is found, the word is spelled. Capitalization coding occurs regardless.
- Any input bytes with special meaning are escaped by prefixing with 06: 06, 0C, 0E, 40 or 7F, 80-FF.
WRT has additional capabilities depending on input, such as skipping encoding if little or no text is detected. The dictionary format is one word per line (linefeed only) with a 13 line header.
If there was a future entry into the Hutter Prize which substantially cut down the compressed size, and that future entry contained fewer rather than more rules about how the English language worked, I would be very surprised and consider that to go a long way towards invalidating my model of what it means to "understand" something.
Here is an example of a large file that:
- contains actual, real information (it is not just random noise)
- it'll compress easily (there's structure to it)
- it's totally useless to you (you can derive structure, but not meaning)
It's 1 megabyte of telemetry captured from a real-time hardware/software system using a binary encoding for the message frames. The telemetry is, in other words, not self-describing.
Some facts:
- A trivial compressor, e.g. zip, can compress this telemetry to a much smaller size.
- It can also decompress the telemetry.
- The size of the compressed file + the size of the compressor is less than the uncompressed telemetry.
However:
You cannot make any conclusions about the meaning of this data, even after you derive some type of structure from it.
Knowing that a 4 byte sequence starting at data[N * 20] for each integer N can be delta-encoded such that on average the delta-encoding of data[(N-1) * 20] saves more space than including both data[(N-1) * 20] and data[N * 20] does not tell you what those 4 bytes mean.
- You can argue that maybe it's a 4 byte value of some type.
But you don't know if it's stored as Big Endian or Little Endian in this format. - You also don't know if it is signed or unsigned, or if it is even a 2's complement integer.
It could be an IEEE 754 32-bit floating point value. - It could be a contiguous run of 2 separate 2 byte values that for some reason are correlated in such a way that they can be delta-encoded together efficiently, e.g. the sensor readings of redundant sensors measuring the same physical process, like a temperature.
- Let's say that for some reason you're certain it is representing an unsigned 4-byte integer.
What does it mean?- Is it the value of some sensor, as a rounded integer, like a distance measured in meters where we drop the fractional part?
- Or are we actually using some type of encoding where we record the sensor value as a integer, but we have a calibration table we apply when post-processing this table to calculate a real physical value, like the look-up table used for thermocouples when interpreting the raw count measured on an ADC?
- If it's the latter and you don't know what look-up table to use (what type of thermocouple is it? Type-K? Type-J?), good luck. Ditto for encoding where the actual physical value is calculated using coefficients for some linear or exponential transform, including an offset.
- The same arguments apply if we try to assume it is a floating point value.
If you think this is being unfair because the original question was about image frames, the encoding that has been suggested in the comments for what image data looks like is describing a bitmap -- a very simple, trivial way to encode image data, and incredibly inefficient in size for that reason. Even in the case of a bitmap, you're jumping to the conclusion that you can reliably differentiate between an MxN image of 8-bit-per-channel RGB data vs an NxM image of 8-bit-per-channel RGB data, when the alternative might be that is some different size of image using say 16-bit-per-channel RGB data for higher resolution in colors, or maybe it is actually 8-bit-per-channel RGBA data because we're including the alpha component for each pixel, or maybe the data is actually stored as HSL channels, or maybe it's stored as BGR instead of RGB, or maybe the data is actually an MxN image of a 8-bit-per-channel grayscale data, or perhaps 24-bit-per-channel grayscale data. In the latter cases, there are not 3 values per pixel, because it's grayscale! Not to be confused with storing a grayscale image in RGB channels, e.g. by repeating the same value for all 3 channels.
And all of the above is ignoring the elephant in the room: Video codecs are not a series of bitmaps. They are compressed and almost always use inter-frame compression meaning that individual video frames are compressed using knowledge of the previous video frames. Therefore, the actual contents of a video does not look like "a series of frames where each frame is a grid of cells where each cell is 3 values". Likewise, most images on the internet are JPGs and PNGs, which are also compressed, and do not look like a grid of cells of three values.
Ok, but what about cameras?
"an image taken by a modern camera contains a surprisingly large amount of easy-to-decode information about the world, in the information-theoretic sense of the word information"
Cameras used by professional photographers often dump data in a RAW format which may or may not be compressed but is specific to the manufacturer of the camera because it's tied to the actual camera hardware in the same way that my hypothetical telemetry is tied to the hardware/software system.
Here's the Wikipedia list of RAW formats:
.3fr, .ari, .arw, .bay, .braw, .crw, .cr2, .cr3, .cap, .data, .dcs, .dcr, .dng, .drf, .eip, .erf, .fff, .gpr, .iiq, .k25, .kdc, .mdc, .mef, .mos, .mrw, .nef, .nrw, .obm, .orf, .pef, .ptx, .pxn, .r3d, .raf, .raw, .rwl, .rw2, .rwz, .sr2, .srf, .srw, .tif, .x3f
...
Providing a detailed and concise description of the content of raw files is highly problematic. There is no single raw format; formats can be similar or radically different. Different manufacturers use their own proprietary and typically undocumented formats, which are collectively known as raw format. Often they also change the format from one camera model to the next. Several major camera manufacturers, including Nikon, Canon and Sony, encrypt portions of the file in an attempt to prevent third-party tools from accessing them.
Is that "easy to decode"?
There is an argument here that it is still easy because all you need to do is "just" run through all of the various permutations I've described above until at the end of the process there is an image that "looks like" a reasonable image. I mean if you dump the color data and it looks like blue and red are swapped, maybe it was stored BGR instead of RGB, and there's no harm there, right? And now we've buried the whole argument with a question of what does it mean for a result to look "reasonable"? When you're given a totally unknown encoding and you want to decode it, and you have to make assumptions about what the parsed data is going to look like just to evaluate the strength of your decoding, is that very solid ground? Are you certain that the algorithm being described here is "easy", in the sense that is computationally efficient?
"you're jumping to the conclusion that you can reliably differentiate between..."
I think you absolutely can, and the idea was already described earlier.
You pay attention to regularities in the data. In most non-random images, pixels near to each other are similar. In an MxN image, the pixel below is a[i+M], whereas in an NxM image, it's a[i+N]. If, across the whole image, the difference between a[i+M] is less than the difference between a[i+N], it's more likely an MxN image. I expect you could find the resolution by searching all possible resolutions from 1x<length> to <length>x1, and finding which minimizes average distance of "adjacent" pixels.
Similarly (though you'd likely do this first), you can tell the difference between RGB and RGBA. If you have (255, 0, 0, 255, 0, 0, 255, 0, 0, 255, 0, 0), this is probably 4 red pixels in RGB, and not a fully opaque red pixel, followed by a fully transparent green pixel, followed by a fully transparent blue pixel in RGBA. It could be 2 pixels that are mostly red and slightly green in 16 bit RGB, though. Not sure how you could piece that out.
Aliens would probably do a different encoding. We don't know what the rods and cones in their eye-equivalents are, and maybe they respond to different colors. Maybe it's not Red Green Blue, but instead Purple Chartreuse Infrared. I'm not sure this matters. It just means your eggplants look red.
I think, even if it had 5 (or 6, or 20) channels, this regularity would be born out, between bit i and bit i+5 being less than bit i and i+1, 2, 3, or 4.
Now, there's still a lot that that doesn't get you yet. But given that there are ways to figure out those, I kinda think I should have decent expectations there's ways to figure out other things, too, even if I don't know them.
I do also think it's important to zoom out to the original point. Eliezer posed this as an idea about AGI. We currently sometimes feed images to our AIs, and when we do, we feed them as raw RGB data, not encoded, because we know that would make it harder for the AI to figure out. I think it would be very weird, if we were trying to train an AI, to send it compressed video, and much more likely that we do, in fact, send it raw RGB values frame by frame.
I will also say that the original claim (by Eliezer, not the top of this thread), was not physics from one frame, but physics from like, 3 frames, so you get motion, and acceleration. 4 frames gets you to third derivatives, which, in our world, don't matter that much. Having multiple frames also aids in ideas like the 3d -> 2d projection, since motion and occlusion are hints at that.
And I think the whole question is "does this image look reasonable", which you're right, is not a rigorous mathematical concept. But "'looks reasonable' is not a rigorous concept" doesn't get followed by "and therefore is impossible" Above are some of the mathematical descriptions of what 'reasonable' means in certain contexts. Rendering a 100x75 image as 75x100 will not "look reasonable". But it's not beyond thinking and math to determine what you mean by that.
The core problem remains computational complexity.
Statements like "does this image look reasonable" or saying "you pay attention to regularities in the data", or "find the resolution by searching all possible resolutions" are all hiding high computational costs behind short English descriptions.
Let's consider the case of a 1280x720 pixel image.
That's the same as 921600 pixels.
How many bytes is that?
It depends. How many bytes per pixel?[1] In my post, I explained there could be 1-byte-per-pixel grayscale, or perhaps 3-bytes-per-pixel RGB using [0, 255] values for each color channel, or maybe 6-bytes-per-pixel with [0, 65535] values for each color channel, or maybe something like 4-bytes-per-pixel because we have 1-byte RGB channels and a 1-byte alpha channel.
Let's assume that a reasonable cutoff for how many bytes per pixel an encoding could be using is say 8 bytes per pixel, or a hypothetical 64-bit color depth.
How many ways can we divide this between channels?
If we assume 3 channels, it's 1953.
If we assume 4 channels, it's 39711.
Also if it turns out to be 5 channels, it's 595665.
This is a pretty fast growing function. The following is a plot.
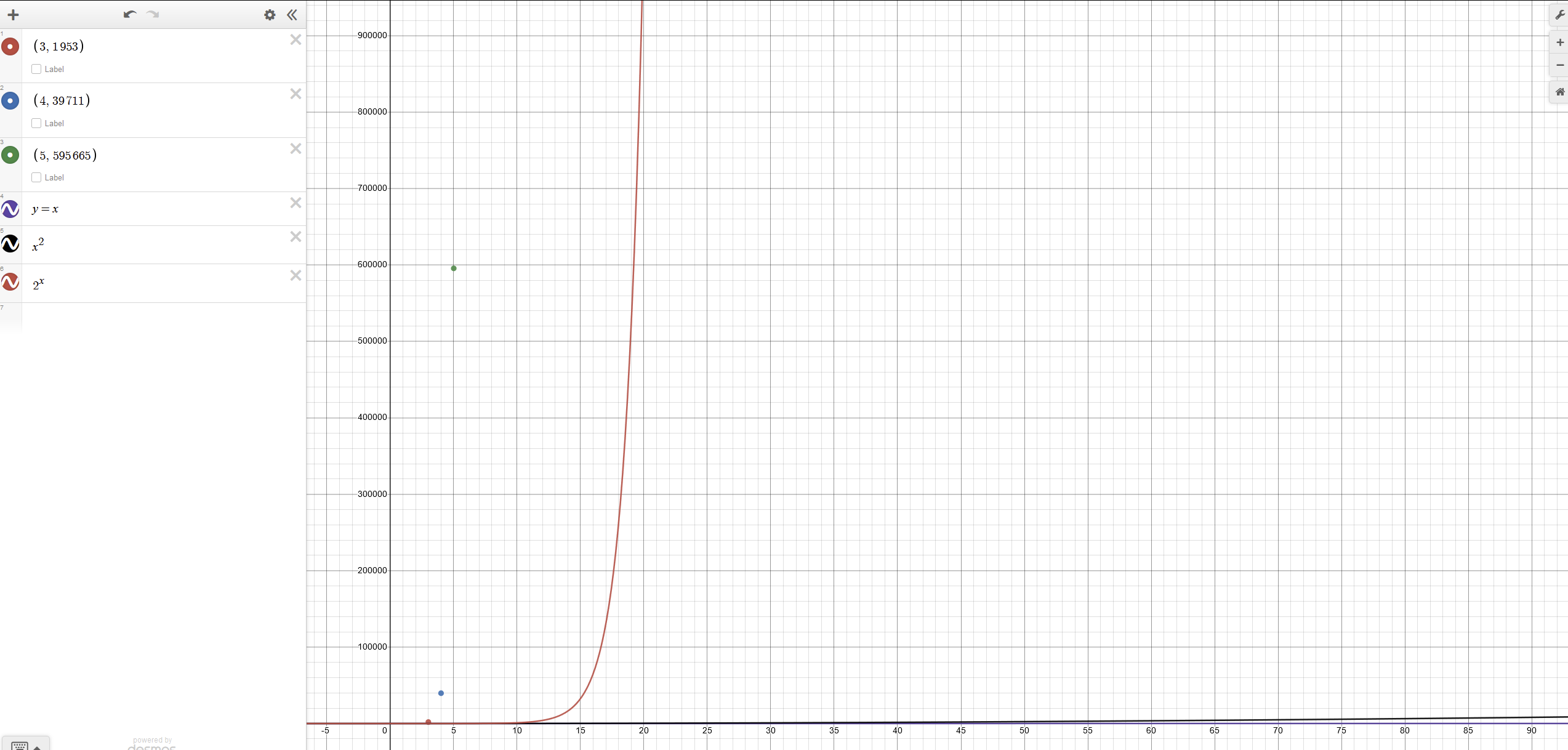
Note that the red line is O(2^N) and the black line barely visible at the bottom is O(N^2). N^2 is a notorious runtime complexity because it's right on the threshold of what is generally unacceptable performance.[2]
Let's hope that this file isn't actually a frame buffer from a graphics card with 32 bits per channel or a 128 bit per pixel / 16 byte per pixel.
Unfortunately, we still need to repeat this calculation for all of the possibilities for how many bits per pixel this image could be. We need to add in the possibility that it is 63 bits per pixel, or 62 bits per pixel, or 61 bits per pixel.
In case anyone wants to claim this is unreasonable, it's not impossible to have image formats that have RGBA data, but only 1 bit associated with the alpha data for each pixel. [3]
And for each of these scenarios, we need to question how many channels of color data there are.
- 1? Grayscale.
- 2? Grayscale, with an alpha channel maybe?
- 3? RGB, probably, or something like HSV.
- 4? RGBA, or maybe it's the RGBG layout I described for a RAW encoding of a Bayer filter, or maybe it's CMYK for printing.
- 5? This is getting weird, but it's not impossible. We could be encoding additional metadata into each pixel, e.g. distance from the camera.
- 6? Actually, this question how how many channels there are is very important, given the fast growing function above.
- 7? This one question, if we don't know the right answer, is sufficient to make this algorithm pretty much impossible to run.
- 8? When we say we can try all of options, that's not actually possible.
- 9? What I think people mean is that we can use heuristics to pick the likely options first and try them, and then fall back to more esoteric options if the initial results don't make sense.
- 10? That's the difference between average run-time and worst case run-time.
- 11? The point that I am trying to make is that the worst case run-time for decoding an arbitrary binary file is pretty much unbounded, because there's a ridiculous amount of choice possible.
- 12? Some examples of "image" formats that have large numbers of channels per "pixel" are things like RADAR / LIDAR sensors, e.g. it's possible to have 5 channels per pixel for defining 3D coordinates (relative to the sensor), range, and intensity.
You actually ran into this problem yourself.
Similarly (though you'd likely do this first), you can tell the difference between RGB and RGBA. If you have (255, 0, 0, 255, 0, 0, 255, 0, 0, 255, 0, 0), this is probably 4 red pixels in RGB, and not a fully opaque red pixel, followed by a fully transparent green pixel, followed by a fully transparent blue pixel in RGBA. It could be 2 pixels that are mostly red and slightly green in 16 bit RGB, though. Not sure how you could piece that out.
Summing up all of the possibilities above is left as an exercise for the reader, and we'll call that sum K.
Without loss of generality, let's say our image was encoded as 3 bytes per pixel divided between 3 RGB color channels of 1 byte each.
Our 1280x720 image is actually 2764800 bytes as a binary file.
But since we're decoding it from the other side, and we don't know it's 1280x720, when we're staring at this pile of 2764800 bytes, we need to first assume how many bytes per pixel it is, so that we can divide the total bytes by the bytes per pixel to calculate the number of pixels.
Then, we need to test each possible resolutions as you've suggested.
The number of possible resolutions is the same as the number of divisors of the number of pixels. The equation for providing an upper bound is exp(log(N)/log(log(N)))[4], but the average number of divisors is approximately log(N).
Oops, no it isn't!
Files have headers! How large is the header? For a bitmap, it's anywhere between 26 and 138 bytes. The JPEG header is at least 2 bytes. PNG uses 8 bytes. GIF uses at least 14 bytes.
Now we need to make the following choices:
- Guess at how many bytes per pixel the data is.
- Guess at the length of the header. (maybe it's 0, there is no header!)
- Calculate the factorization of the remaining bytes N for the different possible resolutions.
- Hope that there isn't a footer, checksum, or any type of other metadata hanging out in the sea of bytes. This is common too!
Once we've made our choices above, then we multiply that by log(N) for the number of resolutions to test, and then we'll apply the suggested metric. Remember that when considering the different pixel formats and ways the color channel data could be represented, the number was K, and that's what we're multiplying by log(N).
In most non-random images, pixels near to each other are similar. In an MxN image, the pixel below is a[i+M], whereas in an NxM image, it's a[i+N]. If, across the whole image, the difference between a[i+M] is less than the difference between a[i+N], it's more likely an MxN image. I expect you could find the resolution by searching all possible resolutions from 1x<length> to <length>x1, and finding which minimizes average distance of "adjacent" pixels.
What you're describing here is actually similar to a common metric used in algorithms for automatically focusing cameras by calculating the contrast of an image, except for focusing you want to maximize contrast instead of minimize it.
The interesting problem with this metric is that it's basically a one-way function. For a given image, you can compute this metric. However, minimizing this metric is not the same as knowing that you've decoded the image correctly. It says you've found a decoding, which did minimize the metric. It does not mean that is the correct decoding.
A trivial proof:
- Consider an image and the reversal of that image along the horizontal axis.
- These have the same metric.
- So the same metric can yield two different images.
A slightly less trivial proof:
- For a given "image" of
Nbytes of image data, there are2^(N*8)possible bit patterns. - Assuming the metric is calculated as an 8-byte IEEE 754 double, there are only
2^(8*8)possible bit patterns. - When
N > 8, there are more bit patterns than values allowed in a double, so multiple images need to map to the same metric.
The difference between our 2^(2764800*8) image space and the 2^64 metric is, uhhh, 10^(10^6.8). Imagine 10^(10^6.8) pigeons. What a mess.[5]
The metric cannot work as described. There will be various arbitrary interpretations of the data possible to minimize this metric, and almost all of those will result in images that are definitely not the image that was actually encoded, but did minimize the metric. There is no reliable way to do this because it isn't possible. When you have a pile of data, and you want to reverse meaning from it, there is not one "correct" message that you can divine from it.[6] See also: numerology, for an example that doesn't involve binary file encodings.
Even pretending that this metric did work, what's the time complexity of it? We have to check each pixel, so it's O(N). There's a constant factor for each pixel computation. How large is that constant? Let's pretend it's small and ignore it.
So now we've got K*O(N*log(N)) which is the time complexity of lots of useful algorithms, but we've got that awkward constant K in the front. Remember that the constant K reflects the number of choices for different bits per pixel, bits per channel, and the number of channels of data per pixel. Unfortunately, that constant is the one that was growing a rate best described as "absurd". That constant is the actual definition of what it means to have no priors. When I said "you can generate arbitrarily many hypotheses, but if you don't control what data you receive, and there's no interaction possible, then you can't rule out hypotheses", what I'm describing is this constant.
I think it would be very weird, if we were trying to train an AI, to send it compressed video, and much more likely that we do, in fact, send it raw RGB values frame by frame.
What I care about is the difference between:
1. Things that are computable.
2. Things that are computable efficiently.
These sets are not the same.
Capabilities of a superintelligent AGI lie only in the second set, not the first.
It is important to understand that a superintelligent AGI is not brute forcing this in the way that has been repeatedly described in this thread. Instead the superintelligent AGI is going to use a bunch of heuristics or knowledge about the provenance of the binary file, combined with access to the internet so that it can just lookup the various headers and features of common image formats, and it'll go through and check all of those, and then if it isn't any of the usual suspects, it'll throw up metaphorical hands, and concede defeat. Or, to quote the title of this thread, intelligence isn't magic.
- ^
This is often phrased as bits per pixel, because a variety of color depth formats use less than 8 bits per channel, or other non-byte divisions.
- ^
Refer to https://accidentallyquadratic.tumblr.com/ for examples.
- ^
A fun question to consider here becomes: where are the alpha bits stored? E.g. if we assume 3 bytes for RGB data, and then we have the 1 alpha bit, is each pixel taking up 9 bits, or are the pixels stored in runs of 8 pixels followed by a single "alpha" pixel with 8 bits describing the alpha channels of the previous 8 pixels?
- ^
- ^
- ^
The way this works for real reverse engineering is that we already have expectations of what the data should look like, and we are tweaking inputs and outputs until we get the data we expected. An example would be figuring out a camera's RAW format by taking pictures of carefully chosen targets like an all white wall, or a checkerboard wall, or an all red wall, and using the knowledge of those targets to find patterns in the data that we can decode.
So, I want to note a few things. The original Eliezer post was intended to argue against this line of reasoning:
I occasionally run into people who say something like, "There's a theoretical limit on how much you can deduce about the outside world, given a finite amount of sensory data."
He didn't worry about compute, because that's not a barrier on the theoretical limit. And in his story, the entire human civilization had decades to work on this problem.
But you're right, in a practical world, compute is important.
I feel like you're trying to make this take as much compute as possible.
Since you talked about headers, I feel like I need to reiterate that, when we are talking to a neural network, we do not add the extra data. The goal is to communicate with the neural network, so we intentionally put it in easier to understand formats.
In the practical cases for this to come up (e.g. a nascent superintelligence figuring out physics faster than we expect), we probably will also be inputting data in an easy to understand format.
Similarly, I expect you don't need to check every possible esoteric format. The likelihood of the image using an encoding like 61 bits per pixel, with 2 for red, 54 for green and 5 for blue is just, very low, a priori. I do admit I'm not sure if only using "reasonable" formats would cut down the possibilities into the computable realm (obviously depends on definitions of reasonable, though part of me feels like you could (with a lot of work) actually have an objective likeliness score of various encodings). But certainly it's a lot harder to say that it isn't than just saying "f(x) = (63 pick x), grows very fast."
Though, since I don't have a good sense for whether "reasonable" ones would be a more computable number, I should update in your direction. (I tried to look into something sort of analogous, and the most common 200 passwords cover a little over 4% of all used passwords, which, isn't large enough for me to feel comfortable expecting that the most "likely" 1,000 formats would cover a significant quantity of the probability space, or anything.)
(Also potentially important. Modern neural nets don't really receive things as a string of bits, but instead as a string of numbers, nicely split up into separate nodes. (yes, those numbers are made of bits, but they're floating point numbers, and the way neural nets interact with them is through all the floating point operations, so I don't think the neural net actually touches the bit representation of the number in any meaningful way.)
Here is an example of a large file that:
I don't see the file, but again if you want to run this the mentioned dates from the other thread work best.
I am not exactly sure what you mean by the phrase "derive structure but not meaning" - a couple possibilities come to mind.
Let's say I have a file that is composed of 1,209,600 bytes of 0s. That file was generated by taking pressure readings, in kPa, once per second on the Hubble Space Telescope for a two week period. If I said "this file is a sequence of 2^11 x 3^3 x 5^2 x 7 zeros", would that be a minimal example of "deriving the structure but not the meaning"? If so I expect that situation to be pretty common.
If not, some further questions:
- Is it coherent to "understand the meaning but not the structure"?
- Would it be possible to go from "understands the structure but not the meaning" to "understands both" purely through receiving more data?
- If not , what about through interaction
- If not, what differences would you expect to observe between a world where I understood the structure but not the meaning of something and a world where I understood both?
I was describing a file that would fit your criteria but not be useful. I was explaining in bullet points all of the reasons why that file can't be decoded without external knowledge.
I think that you understood the point though, with your example of data from the Hubble Space Telescope. One caveat: I want to be clear that the file does not have to be all zeroes. All zeroes would violate your criteria that the data cannot be compressed to less than 10% of it's uncompressed size, since all zeroes can be trivially run-length-encoded.
But let's look at this anyway.
You said the file is all zeroes, and it's 1209600 bytes. You also said it's pressure readings in kPa, taken once per second. You then said it's 2^11 x 3^3 x 5^2 x 7 zeroes -- I'm a little bit confused on where this number came from? That number is 9676800, which is larger than the file size in bytes. If I divide by 8, then I get the stated file size, so maybe you're referring to the binary sequence of bits being either 0 or 1, and then on this hardware a byte is 8-bits, and that's how those numbers connect.
In a trivial sense, yes, that is "deriving the structure but not the meaning".
What I really meant was that we would struggle to distinguish between:
- The file is 1209600 separate measurements, each 1-byte, taken by a single pressure sensor.
- The file is 604800 measurements of 1 byte each from 2 redundant pressure sensors.
- The file is 302400 measurements, each 4-bytes, taken by a single pressure sensor.
- The file is 241920 measurements, each a 4-byte timestamp field and a 1-byte pressure sensor value.
Or considering some number of values, with some N-byte width:
- The pressure sensor value is in kPa.
- The pressure sensor value is in psi.
- The pressure sensor value is in atmospheres.
- The pressure sensor value is in lbf.
- The pressure sensor value is in raw counts because it's a direct ADC measurement, so it needs to be converted to the actual pressure via a linear transform.
- We don't know the ADC's reference voltage.
- Or the data sheet for this pressure sensor.
Your questions are good.
1. Is it coherent to "understand the meaning but not the structure"?
Probably not? I guess there's like a weird "gotcha" answer to this question where I could describe what a format tells you, in words, but not show you the format itself, and maybe we could quibble that in such a scenario you'd understand "the meaning but not the structure".
EDIT: I think I've changed my mind on this answer since posting -- yes, there are scenarios where you would understand the meaning of something, but not necessarily the structure of it. A trivial example would be something like a video game save file. You know that some file represents your latest game, and that it allows you to continue and resume from where you left off. You know how that file was created (you pressed "Save Game"), and you know how to use it (press "Load Game", select save game name), but without some amount of reverse-engineering, you don't know the structure of it (assuming that the saved game is not stored as plain text). For non-video-game examples, something like a calibration file produced by some system where the system can both 1.) produce the calibration via some type of self-test or other procedure, and 2.) receive that calibration file. Or some type of system that can be configured by the user, and then you can save that configuration file to disc, so that you can upload it back to the system. Maybe you understand exactly what the configuration file will do, but you never bothered to learn the format of the file itself.
2. Would it be possible to go from "understands the structure but not the meaning" to "understands both" purely through receiving more data?
In general, no. The problem is that you can generate arbitrarily many hypotheses, but if you don't control what data you receive, and there's no interaction possible, then you can't rule out hypotheses. You'd have to just get exceedingly lucky and repeatedly be given more data that is basically designed to be interpreted correctly, i.e. the data, even though it is in a binary format, is self-describing. These formats do exist by the way. It's common for binary formats to include things like length prefixes telling you how many bytes follow some header. That's the type of thing you wouldn't notice with a single piece of data, but you would notice if you had a bunch of examples of data all sharing the same unknown schema.
3. If not , what about through interaction
Yes, this is how we actually reverse-engineer unknown binary formats. Almost always we have some proprietary software that can either produce the format, or read the format, and usually both. We don't have the schema, and for the sake of argument let's say we don't want decompile the software. An example: video game save files that are stored using some ad-hoc binary schema.
What we generally do is start poking known values into the software and seeing what the output file looks like -- like a specific date time, a naming something a certain field, or making sure some value or checkbox is entered in a specific way. Then we permute that entry and see how the file changes. The worse thing would be if almost the entire file changes, which tells us the file is either encrypted OR it's a direct dump of RAM to disk from some data structure with undefined ordering, like a hash map, and the structure is determined by keys which we haven't figured out yet.
Likewise, we do the reverse. We change the format and we plug it back into the software (or an external API, if we're trying to understand how some website works). What we're hoping for is an error message that gives us additional information -- like we change some bytes and now it complains a length is invalid, that's probably related to length. Or if we change some bytes and it says the time cannot be negative, then that might be a time related. Or we change any byte and it rejects the data as being invalid, whoops, probably encrypted again.
The key here is that we have the same problem as question 2 -- we can generate arbitrarily many hypotheses -- but we have a solution now. We can design experiments and iteratively rule out hypotheses, over and over, until we figure out the actual meaning of the format -- not just the structure of it, but what values actually represent.
Again, there are limits. For instance, there are reverse-engineered binary formats where the best we know is that some byte needs to be some constant value for some reason. Maybe it's an internal software version? Who knows! We figured out the structure of that value -- the byte at location 0x806 shall be 203 -- but we don't know the meaning of it.
4. If not, what differences would you expect to observe between a world where I understood the structure but not the meaning of something and a world where I understood both?
Hopefully the above has answered this.
Replying to your other post here:
I don't think this algorithm could decode arbitrary data in a reasonable amount of time. I think it could decode some particularly structured types of data, and I think "fairly unprocessed sensor data from a very large number of nearly identical sensors" is one of those types of data.
My whole point is that "unprocessed sensor data" can be arbitrarily tied to hardware in ways that make it impossible to decode without knowledge of that particular hardware, e.g. ADC reference voltages, datasheets, or calibration tables.
RAW I'd expect is better than a bitmap, assuming no encryption step, on the hypothesis that more data is better.
The opposite. Bitmaps are much easier than RAW formats. A random RAW format, assuming no interaction with the camera hardware or software that can read/write that format, might as well be impossible. E.g. consider the description of a RAW format here. Would you have known that the way the camera hardware works involves pixels that are actually 4 separate color sensors arranged as (in this example) an RGBG grid (called a Bayer filter), and that to calculate the pixel colors for a bitmap you need to interpolate between 4 of those raw color sensors for each color channel on each pixel in the bitmap, and the resulting file size is going to be 3x larger? Or that the size of the output image is not the size of the sensor, so there's dead pixels that need to be ignored during the conversion? Again, this is just describing some specific RAW format -- other RAW formats work differently, because cameras don't all use the same type of color sensor.
The point as I see it is more about whether it's possible with a halfway reasonable amount of compute or whether That Alien Message was completely off-base.
It was completely off-base.
BTW I see that someone did a very minimal version (with an array of floating point numbers generated by a pretty simple process) of this test, but I'm still up for doing a fuller test -- my schedule now is a lot more clear than it was last month.
Which question are we trying to answer?
- Is it possible to decode a file that was deliberately constructed to be decoded, without a priori knowledge? This is vaguely what That Alien Message is about, at least in the first part of the post where aliens are sending a message to humanity.
- Is it possible to decode a file that has an arbitrary binary schema, without a priori knowledge? This is the discussion point that I've been arguing over with regard to stuff like decoding CAMERA raw formats, or sensor data from a hardware/software system. This is also the area where I disagree with That Alien Message -- I don't think that one-shot examples allow robust generalization.
I don't think (1) is a particularly interesting question, because last weekend I convinced myself that the answer is yes, you can transfer data in a way that it can be decoded, with very few assumptions on the part of the receiver. I do have a file I created for this purpose. If you want, I'll send you it.
I started creating a file for (2), but I'm not really sure how to gauge what is "fair" vs "deliberately obfuscated" in terms of encoding. I am conflicted. Even if I stick to encoding techniques I've seen in the real world, I feel like I can make choices on this file encoding that make the likelihood of others decoding it very low. That's exactly what we're arguing about on (2). However, I don't think it will be particularly interesting or fun for people trying to decode it. Maybe that's ok?
What are your thoughts?
I'm not sure either one quite captures exactly what I mean, but I think (1) is probably closer than (2), with the caveat that I don't think the file necessarily has to be deliberately constructed to be decoded without a-priori knowledge, but it should be constructed to have as close as possible to a 1:1 mapping between the structure of the process used to capture the data and the structure of the underlying data stream.
I notice I am somewhat confused by the inclusion of camera raw formats in (2) rather than in (1) though -- I would expect that moving from a file in camera raw format to a jpeg would move you substantially in the direction from (1) to (2).
It sounds like maybe you have something resembling "some sensor data of something unusual in an unconventional but not intentionally obfuscated format"? If so, that sounds pretty much exactly like what I'm looking for.
However, I don't think it will be particularly interesting or fun for people trying to decode it. Maybe that's ok?
I think it's fine if it's not interesting or fun to decode because nobody can get a handle on the structure -- if that's the case, it will be interesting to see why we are not able to do that, and especially interesting if the file ends up looking like one of the things we would have predicted ahead of time would be decodable.
⁴ Though I will note that, counter to my expectation here, as far as I know modern lossless photo compression does not look like "build a simulation of some objects in space, fine tune, and apply a correction layer" despite this being what my model of the world predicting humanity would create in a world where computation is cheap and bandwidth is expensive.
Because computing isn't that cheap, and bandwidth isn't that expensive, and no one wants to get their GPU cluster running to save 500 bits of bandwidth.
I think this is a great exercise. I’d also note that the entirety of modern physics isn’t actually all that many bits. Especially if you’re just talking about quantum electrodynamics (which covers ~everything in the frame).
It’s an enormous amount of compute to unfurl those bits into predictions, but the full mathematical description is something you’d encounter pretty early on if you search hypotheses ordered by description length.
4, 5, and 6 are not separate steps - when you only have 1 example, the bits to find an input that generates your output are not distinct from the bits specifying the program that computes output from input.
Yeah my guess is that you almost certainly fail on step 4 - an example of a really compact ray tracer looks like it fits in 64 bytes. You will not do search over all 64 byte programs. Even if you could evaluate 1 of them per atom per nanosecond using every atom in the universe for 100 billion years, you'd only get 44.6 bytes of search.
Let's go with something more modest and say you get to use every atom in the milky way for 100 years, and it takes about 1 million atom-seconds to check a single program. This gets you about 30 bytes of search.
Priors over programs will get you some of the way there, but usually the structure of those priors will also lead to much much longer encodings of a ray tracer. You would also need a much more general / higher quality ray tracer (and thus more bits!) as well as an actually quite detailed specification of the "scene" you input to that ray tracer (which is probably way more bits than the original png).
The reason humans invented ray tracers with so much less compute is that we got ray tracers from physics and way way way more bits of evidence, not the other way around.
You will not do search over all 64 byte programs
I was not imagining you would, no. I was imagining something more along the lines of "come up with a million different hypotheses for what a 2-d grid could encode", which would be tedious for a human but would not really require extreme intelligence so much as extreme patience, and then for each of those million hypotheses try to build a model, and iteratively optimize for programs within that model for closeness to the output.
I expect, though I cannot prove, that "a 2d projection of shapes in a 3d space" is a pretty significant chunk of the hypothesis space, and that all of the following hypotheses would make it into the top million
- The 2-d points represent a rectangular grid oriented on a plane within that 3-d space. The values at each point are determined by what the plane intersects.
- The 2-d points represent a grid oriented on a plane within that 3-d space. The values at each point are determined by drawing lines orthogonal to the plane and seeing what they intersect and where. The values represent distance.
- The 2-d points represent a grid oriented on a plane within that 3-d space. The values at each point are determined by drawing lines orthogonal to the plane and seeing what they intersect and where. The values represent something else about what the lines intersect. 4-6. Same as 1-3, but with a cylinder. 6-9. Same as 1-3, but with a sphere. 10-12. Same as 1-3, but with a torus. 13-21: Same as 4-12 but the rectangular grid is projected onto only part of the cylinder/sphere/torus instead of onto the whole thing.
I am not a superintelligence though, nor do I have any special insight into what the universal prior looks like, so I don't know if that's actually a reasonable assumption or whether it's an entity embedded in a space that detects other things within that space using signals privileging the hypothesis that "a space where it's possible to detect other stuff in that space using signals" is a simple construct.
as well as an actually quite detailed specification of the "scene" you input to that ray tracer (which is probably way more bits than the original png).
If the size-optimal scene such that "ray-trace this scene and then apply corrections from this table" is larger than a naively compressed version of the png, my whole line of thought does indeed fall apart. I don't expect that to be the case, because ray tracers are small and pngs are large, but this is a testable hypothesis (and not just "in principle it could be tested with a sufficiently powerful AI" but rather "an actual human could test it in a reasonable amount of time and effort using known techniques"). I don't at this moment have time to test it, but maybe it's worth testing at some point?
I wrote a reply to a separate comment you made in this thread here, but it's relevant for this comment too. The idea that the data looks like "a 2-d grid" is an assumption true only for uncompressed bitmaps, but not for JPGs, PNGs, RAW, or any video codec. The statement that the limiting factor is "extreme patience" hints that this is really a question asking "what is the computational complexity[1] of an algorithm that can supposedly decode arbitrary data"?
I don't think this algorithm could decode arbitrary data in a reasonable amount of time. I think it could decode some particularly structured types of data, and I think "fairly unprocessed sensor data from a very large number of nearly identical sensors" is one of those types of data.
I actually don't know if my proposed method would work with jpgs - the whole discrete cosine transform thing destroys data in a way that might not leave you with enough information to make much progress. In general if there's lossy compression I expect that to make things much harder, and lossless compression I'd expect either makes it impossible (if you don't figure out the encoding) or not meaningfully different than uncompressed (if you do).
RAW I'd expect is better than a bitmap, assuming no encryption step, on the hypothesis that more data is better.
Also I kind of doubt that the situation where some AI with no priors encounters a single frame of video but somehow has access to 1000 GPU years to analyze that frame would come up IRL. The point as I see it is more about whether it's possible with a halfway reasonable amount of compute or whether That Alien Message was completely off-base.
Priors over programs will get you some of the way there, but usually the structure of those priors will also lead to much much longer encodings of a ray tracer.
If you grant the image being reconstructed, then 2 dimensional space is already in the cards. It's not remotely 64 bits to make the leap to 3d space projected to 2d space. The search doesn't have to be "search all programs in some low-level encoding", it can be weighted on things that are mathematically interesting / elegant (which is a somewhat a priori feature).
I think a decent candidate for what a sufficiently great mind would do, in the absence of priors other than its own existence and the data fed to it... is to enumerate universes with different numbers of dimensions and different fundamental forces and values of physical constants and initial conditions, and see which of them are likely to produce it and the data fed to it. Which, at least in our case, means "a universe in which intelligent life spontaneously developed and made computers".
How do you know your world is 3D, not actually 2D?
There was a book, Flatland, describing a fictional 2D world. One of the issues is... you can't have things like digestive tracts that pass all the way through you, unless you consist of multiple non-connected pieces. I'm not sure I can rule it out entirely—after all, 2D cellular automata can be Turing-complete, and can therefore simulate anything you like—but it seems possible that a sufficiently great mind could say that no 2D universe with laws of physics resembling our own could support life.
Is it actually the case that Occam's razor would prefer "A universe, such as a 3-space 1-time dimensional universe with the following physical constants within certain ranges and a Big Bang that looked like this, developed intelligent life and made me and this data" over "The universe is one big 2D cellular automaton that simulates me and this data, and contains nothing else"? I dunno. Kolmogorov complexity of a machine simulating the universe, I guess? That seems like the right question even if I don't know the answer.
Deriving the laws of physics from an image is completely impossible because the data contained in the image is a tiny piece of the actual system, which is image data + observer. Specifically, there is no way to get from "these bits represent 3 related values, in a grid" to "these values represent different intensities of specific wavelengths of perpendicular electric and magnetic fields propagating through space" Even if that hypothesis could be generated, there is no data about which wavelengths are represented. Nor any information to derive how the light detected by rods and cones gets processed to generate recognition of specific physical things. Nothing in an image says that equal R and G signals means Yellow (or whatever the actual rules are)
When you get much smarter, you don't realize that benefit by screwing extra pennies out of existing bets. You find new bets that you can now be 99% sure of instead of 50%, new things you can do with matter instead of decreasing tweaks to old things.
Yeah, I'm aware of that. I was Illustrating the returns to predictive accuracy in a single domain.
Cross-domain predictive accuracy wasn't investigated here, and it's not clear how much cross-domain predictive accuracy manifests in practice. That is, it's not necessarily the case that if you improved your predictive accuracy in one domain (your predictive accuracy will also rise in other domains).
Are there any theoretical or empirical results suggesting that predictive accuracy generalises?
Google’s GATO perhaps? I’m not sure in which direction it actually points the evidence, but it does suggest the answer is nuanced
Suppose you give 2 people a maths quiz. One person is an average maths undergrad. The other is Terry Tao. The quiz was very easy, it was from the kids book "counting made fun", so both people got all the questions right. You use this to "prove the sharply diminishing returns of maths skill". That's what you are doing with your 99.999% accuracy things.
The human advantage over chimps doesn't look like humans being 99.999% accurate about where the banana is, while chimps are only 99% accurate. That extra accuracy only buys you a tiny extra sliver of banana.
The human intelligence advantage looks like humans having a whole new space of questions that chimps can't comprehend. Some of these, like the electrical conductivity of copper, the mass of the earth, or that there are infinitely many primes are known with great confidence. If you can't figure out the proof, you have basically no clue if there are infinitely many primes, if you can figure it out, your basically certain. In domains where verifying is easier than finding, like maths proofs, then there is a step function from basically no clue to basically certain with a small increase in intelligence.
Reality is full of step functions. Small differences in engineering skill between a rocket working and exploding. A moon mission designed by 10% stupider engineers won't get 90% of the way to the moon and bring back 90% as much moonrock.
AI progress currently looks quite full of big jumps. Lots of papers coming along a few months later with a substantial improvement. There is no law of physics that says making something smart is that hard. If this trend continued, we would expect a fairly rapid ascent into superintelligence, even if humans were doing all the research. Sharply diminishing returns can be a thing. But they only happen when you are pushing close to some physical limits. The human brain is, I suspect, a long long way from any kind of limits.
During my 2017 binge of LW, I recall Yudkowsky suggesting that a superintelligence could infer the laws of physics from a single frame of video showing a falling apple (Newton apparently came up with his idea of gravity from observing a falling apple).
I now think that's somewhere between deeply magical and utter nonsense.
Some details here: You are likely referring to That Alien Message. In my opinion Eliezer Yudkowsky made a weaker claim than you are implying:
A Bayesian superintelligence, hooked up to a webcam, would invent General Relativity as a hypothesis—perhaps not the dominant hypothesis, compared to Newtonian mechanics, but still a hypothesis under direct consideration—by the time it had seen the third frame of a falling apple. It might guess it from the first frame, if it saw the statics of a bent blade of grass.
To me it does not seem hard for a superintelligence (or 1000 years of Einstein-level thinking) to come up with Newtonian mechanics as a hypothesis from three frames of a falling apple. But I am not sure about the (weakly stated) suggestion that you could derive it from a picture of a bent blade of grass.
Epistemic Status
This started out as a shortform and is held to the same epistemic standards that I do for my Twitter account. It however became too long for that medium, so I felt the need to post it elsewhere.
I feel it's better to post my rough and unpolished thoughts than to not post them at all, so hence.
Introduction
One significant way I've changed my views related to risks from strongly superhuman intelligence (compared to 2017 bingeing LW DG) is that I no longer believe intelligence to be "magical".
During my 2017 binge of LW, I recall Yudkowsky suggesting that a superintelligence could infer the laws of physics from a single frame of video showing a falling apple (Newton apparently came up with his idea of gravity from observing a falling apple).I now think that's somewhere between deeply magical and utter nonsense. It hasn't been shown that a perfect Bayesian engine (with [a] suitable [hyper]prior[s]) could locate general relativity or (even just Newtonian mechanics) in hypothesis space from a single frame of video.I'm not even sure a single frame of video of a falling apple has enough bits to allow one to make that distinctionin theory.Edit
The above is based on a false recollection of what Yudkowsky said (I leave it anyway because the comments have engaged with it). Here's the relevant excerpt from "That Alien Message":
I still disagree somewhat with the above, but it's a weaker disagreement — this is a weaker claim than I misrecalled Yudkowsky as making — I apologise for any harm/misunderstanding my carelessness (I should have just tracked down the original post) caused.
I think that I need to investigate at depth what intelligence (even strongly superhuman intelligence) is actually capable of, and not just assume that intelligence can do anything not explicitly forbidden by the fundamental laws. The relevant fundamental laws with a bearing on cognitive and real-world capabilities seem to be:
The Relevant Question: Marginal Returns to Real World Capability of Cognitive Capabilities
I've done some armchair style thinking on "returns to real-world capability" of increasing intelligence, and I think the Yudkowsky style arguments around superintelligence are quite magical.
It seems doubtful that higher intelligence would enable that. E.g. marginal returns to real-world capability from increased predictive power diminish at an exponential rate. Better predictive power buys less capability at each step, and it buys a lot less. I would say that the marginal returns are "sharply diminishing".
An explanation of "significantly/sharply diminishing":
Sharply Diminishing Marginal Returns to Real World Capabilities From Increased Predictive Accuracy
A sensible way of measuring predictive accuracy is something analogous to −log(error rate). The following transitions:
All make the same incremental jump in predictive accuracy.
We would like to measure the marginal return to real-world capability of increased predictive accuracy. The most compelling way I found to operationalise "returns to real-world capability" was monetary returns.
I think that's a sensible operationalization:
(I will however be interested in other operationalisations of "returns to real-world capability" that show different results).
The obvious way to make money from beliefs in propositions is by bets of some form. One way to place a bet and reliably profit is insurance. (Insurance is particularly attractive because in practice, it scales to arbitrary confidence and arbitrary returns/capital).
Suppose that you sell an insurance policy for event X, and for each prospective client Ci, you have a credence that X would not occur to them P(¬X|Ci). Suppose also that you sell your policy at $1,000,000.
At a credence of 90%, you cannot sell your policy for <$100,000. At a price of $100,000 and given the credence of 90%, your expected returns will be $0 for that customer. Assume the given customer is willing to pay at most $100,000 for the policy.
If your credence in X not happening increased, how would your expected returns change? This is the question we are trying to investigate to estimate real-world capability gains from increased predictive accuracy.
The results are below:
As you can see, the marginal returns from linear increases in predictive accuracy are give by the below sequence: {$900000,$90000,$9000,$900,$90,$9,...}
f(n)=$900000$900000×10−n=11×10−n=10nf(n)∈o(10n)(This construction could be extended to other kinds of bets, and I would expect the result to generalise [modulo some minor adjustments] to cross-domain predictive ability.
Alas,
a shortform[this started as a shortform but ended up crossing the 1,000 words barrier, so I moved it] is not the place for such elaboration).Thus returns to real-world capability of increased predictive accuracy are sharply diminishing.
One prominent class of scenario in which the above statement is false is when competing against other agents. In competitions with "winner take all" dynamics, better predictive accuracy has more graceful returns. I'll need to think further about various multi agent scenarios and model them better/in more detail.
Marginal Returns to Real World Capabilities From Other Cognitive Capabilities
Of course, predictive accuracy is just one aspect of intelligence, there are many others:
And we'd want to investigate the relationship for aggregate cognitive capabilities/"general intelligence". The example I illustrated earlier merely sought to demonstrate how returns to real-world capability could be "sharply diminishing".
Marginal Returns to Cognitive Capabilities
Another inquiry that's important to determining what intelligence is actually capable of is the marginal returns to investment of cognitive capabilities towards raising cognitive capabilities.
That is if an agent was improving its own cognitive architecture (recursive self improvement) or designing successor agents, how would the marginal increase in cognitive capabilities across each generation behave? What function characterises it?
Marginal Returns of Computational Resources
This isn't even talking about the nature of marginal returns to predictive accuracy from the addition of extra computational resources.
By "computational resources" I mean the following:
That could further bound how much capability you can purchase with the investment of additional economic resources. If those also diminish "significantly" or "sharply", the situation becomes that much bleaker.
Marginal Returns to Cognitive Reinvestment
The other avenue to raising cognitive capabilities is the investment of cognitive capabilities themselves. As seen when designing successor agents or via recursive self-improvement.
We'd also want to investigate the marginal returns to cognitive reinvestment.
My Current Thoughts
Currently, I think strongly superhuman intelligence would require herculean effort. I am much less confident that bootstrapping to ASI would necessarily be as easy as recursive self-improvement or "scaling" up the expenditure of computational resources. I'm unconvinced that a hardware overhang would be sufficient (marginal returns may diminish too fast for it to be sufficient).
I currently expect marginal returns to real-world capability will diminish significantly or sharply for many cognitive capabilities (and the aggregate of them) across some "relevant cognitive intervals".
I suspect that the same will prove to be true for marginal returns to cognitive capabilities of investing computational resources or other cognitive capabilities.
I don't plan to rely on my suspicions and would want to investigate these issues at extensive depth (I'm currently planning to pursue a Masters and afterwards PhD, and these are the kinds of questions I'd like to research when I do so).
By "relevant cognitive intervals", I am gesturing at the range of general cognitive capabilities an agent might belong in.
Humans being the only examples of general intelligence we are aware of, I'll use them as a yardstick.
Some "relevant cognitive intervals" that seem particularly pertinent:
Conclusions and Next Steps
The following questions:
(Across the cogntive intervals of interest).
Are questions I plan to investigate in depth in the future.