LESSWRONG
LW

Comment Permalink
So8res*Ω9150

various attempts to distill my objection:

the details of the omitted "zip" operation are going to be no simpler than the standard proof of löb's theorem, and will probably turn out to be just a variation on the standard proof of löb's theorem (unless you can find a way of building self-reference that's shorter than the Y combinator (b/c the standard proof of löb's theorem is already just the Y combinator plus the minimal modifications to interplay with gödel-codes))

even more compressed: the normal proof of löb is contained in the thing labeled "zip". the argument in the OP is operating under the assumption that a proof can make reference to its own gödel-number, and that assumption is essentially just löb's theorem.

a thing that might help is asking what specific proof-steps the step "1. the gödel-code P of this very proof proves C" cashes out into. obviously step 1 can't cash out into verifying (under quotation) every step of the entire proof (by checking for the appropriate prime-factors), because then the proof would require at least one step for every step in the proof plus three extra steps at the end, which would make the proof infinite (and infinite proofs admit contradictions).

so step 1 has to involve some indirection somehow. (cf: we can't get a fixpoint in λ-calculus by f (f (f ..., we need some indirection, as occurs in (Y f) aka (λ s. f (s s)) (λ s. f (s s)), to make the term finite.)

this works fine, as long as you are ok w/ the gödel-code in step 1 being not P, but some different proof of the same conclusion (analogous to the difference between f (Y f) and Y f), and so long as you have the analog of the Y combinator (modified to interplay with gödel-codes).

but the analog of the Y combinator is precisely löb's theorem :-p

if i understand your OP correctly, we can factor it into three claims:

  1. when proving C, it's valid to assume a referece «this» to the gödel-code of a proof of C
  2. given (1) and a proof f of □ C → C, there's a proof of C by simply applying f to «this»
  3. you can arrange things such that if you desugar «this» into a particular numeral in "f «this»", you'll find that that numeral is the gödel-code of "f «this»".

(1) is löb's theorem.

(2) is an indirect proof of löb's theorem, from the assumption of löb's theorem (in direct analogy with how, once we've found syntax Y f for the fixpoint of f, we can wrap it in f to find an alternate syntax, namely f (Y f)).

(3) is false (i'm fairly confident)--you can get real close, but you can't quite get there (in direct analogy to how you can get λ-term Y f that means the same thing as f (Y f), but you can't get a λ-term fix f that is syntactically exactly f (fix f), on pain of infinite syntax).

afaict, there's two ways to read this proposal (if we port across the analogy to λ-calculus), according to whether you cash "zip" out to a recursive instance of the whole proposal, vs whether you cash "zip" out to some different proof of löb's theorem:

  1. "i hear that people find the Y combinator confusing. instead of using (Y f) to name the fixpoint of f, why not use f (f (f (f (... ad infinitum?"

  2. "i hear that people find the Y combinator confusing. instead of using (Y f) to name the fixpoint of f, why not use f (Y f)?"

the answer to (1) is that it doesn't make sense unless you allow infinite syntax trees (which aren't permitted in normal math b/c infinite proofs admit contradictions).

the answer to (2) is that, while (Y f) may be somewhat tricky to grasp, f (Y f) is surely no simpler :-p

Reply
See in context
by Andrew_Critch
AI Alignment Forum
3 min read
35

58

Ω 32

Motivation

Löb's theorem is pretty counterintuitive.  Speaking informally about one or more agents engaging in logically valid reasoning, the theorem says something like this:

  • "If it's believed that believing a particular prophesy would cause it to self-fulfill, then the prophecy will be believed." 

Formally, the theorem just says  , where   means " is provable". This is most weird if X is a false statement, because it means you can't prove that you can't prove X (Gödel's theorem).

(Also: the box symbol above is not an unrendered symbol; it's supposed to be a box.)

Meta-motivation

I'd like to make Löb's theorem more intuitive for humans, because it shows how agents can sidestep the need to mentally simulate each other in games, by instead using reasoning/arguments that happen to self-fulfill in a good and defensible way.  Basically, Löbian reflection helps agents to avoid metacognitive stack overflows when thinking about themselves and each other, and I want more human beings to understand how that can work, and sometimes already does work, in real world agents.

State of the art

The best attempt I've seen to make Löb's theorem more intuitive is Eliezer Yudkowsky's Cartoon Guide to Löb's Theorem, which is still quite confusing.  The confusingness comes from thinking about a self-referential statement ( on Wikipedia; S on Arbital) that's used to carry out the proof.  The statement basically says "If this statement is provable, then C."  Dealing with that sentence is pretty cumbersome, and requires a lot of fiddling around with nested statements and implications.

Doing better

I think we can make a new proof of Löb's theorem that doesn't use that weird self-referential sentence, by instead making the proof of Löb's theorem itself self-referential.  Page 15 of the following paper poses an open problem on how to do this, which I think is possible to resolve affirmatively:

Here's a screenshot from it:

If we can make a proof like that work, we could then use the following much shorter and simpler cartoon guide to explain it:

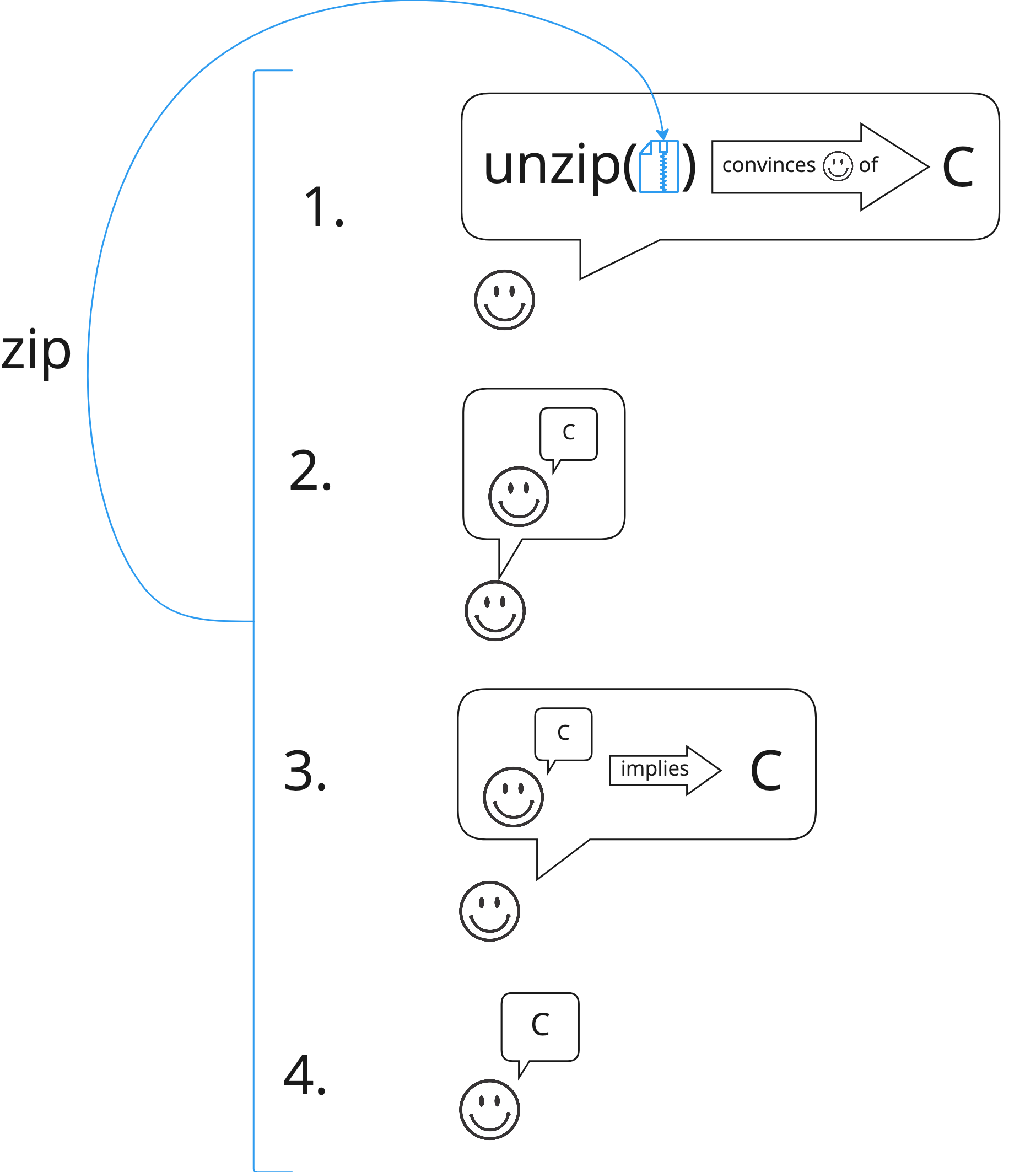
In other words, I want to write a proof of Löb's theorem that is structured much like a Quine.  I'd like the details to (eventually) be really crisp and readable, so it can be peer reviewed for correctness, at a level of rigor comparable to this earlier paper on Löb's theorem for proof systems with bounded length:

As a possible start to writing such a proof, I think some of the same machinery  (e.g., the diagonal lemma) from Boolos's textbook "The Logic of Provability" can be used to cook up self-referential proofs fitting the cartoon template above... thereby making Löb's theorem less mysterious and more intuitive forever.  

Further meta-motivation (added Nov 26)

A key reason I'm interested in having a self-referential self-validating proof, rather than a normal-ish proof about a sentence that is self-referential (like  on Wikipedia), is that human documents often refer to themselves, but human sentences rarely refer directly to themselves in isolation.  This sentence is an exception, but such utterances are generally rare.  So, making Löb more intuitive to humans either means

  1. making humans more accustomed to thinking about sentences that refer to themselves (so the traditional proof of Löb can be more intuitive), or
  2. finding a new proof that self-references in a way that's more like the way a human document refers to itself.  

The aim of this post is to try for the second approach.  Notice how you didn't think the previous sentence was weirdly self-referential?  That's because it referred to the whole document that it's part of, rather than just narrowly referring directly to itself.  I'm not quite sure why humans are more comfortable with that than with directly-and-narrowly self-referential sentences.  Maybe it's because I thing needs to have enough non-self-referential content before humans will care about it enough to tolerate it talking about itself.  I'm not sure.

Countering naive impossibility arguments (added Nov 26)

It's in fact possible to use Löb's theorem to construct a self-referential proof of the kind illustrated above.  So, naive arguments that "Proofs can't be self-referential like that" are not going to hold up.  The hard thing I'm asking for is to make such a proof — of Löb's theorem specifically — without going through the traditional proof of Löb, i.e., without using a narrowly-and-directly-self-referential sentence (like  on Wikipedia).

Difficulty assessment

I think getting a Qunean proof to work here is probably a bit easier than the JSL paper linked directly above.  Like, I think if I spent 3 months on it (which is how long the JSL paper took), then I could do it.  I do think getting it right involves mentally syncing with some fundamental and standard machinery in provability logic, which can take a bit of time if you've never worked in the area before (as I hadn't).

Anyway, if you can figure out how to write this proof, please post your solution or solution attempts here :)

Löb's theoremHas DiagramOpen ProblemsQuinesWorld Modeling
Frontpage

58

Ω 32

Mentioned in
Open technical problem: A Quinean proof of Löb's theorem, for an easier cartoon guide
New Comment
35 comments, sorted by
top scoring
Click to highlight new comments since:
[-]So8res*Ω16323

(Epistemic status: quickly-recounted lightly-edited cached state that I sent in response to an email thread on this topic, that I now notice had an associated public post. Sorry for the length; it was easier to just do a big unfiltered brain-dump than to cull, with footnotes added.)

here's a few quick thoughts i have cached about the proof of löb's theorem (and which i think imply that the suggested technique won't work, and will be tricky to repair):

#1. löb's theorem is essentially just the Y combinator, but with an extra level of quotation mixed in.[1]

Y : (A → A) → A
Y f := let g be (λ s. f (s s)) in g g

löb : □ (□ A → A) → □ A
löb f := let g be (λ s. f (s "s")) in g "g"

the standard proof of löb's theorem (e.g. as it appears in the cartoon guide) is complicated by two points:

1a. one thing we need here is that the variable s is sensical, and in particular we need some S with S ≃ (□ S → A). the existence of such an S follows from the diagonal lemma.[2]

1b. the other thing we need here is to show that quotation and normal proof steps (function application or modus ponens or whatever) interact in the "obvious way", and don't gum each other up. for instance, we need that □(A → B) ∧ □(A) yields □(B), showing that we can "apply quoted functions to quoted arguments", in order for syntax like f (s "s") to be sensical.

if i were trying to make a guide to löb's theorem today, i'd break it down as above; for me, at least, this breakdown is significantly more intuitive than the cartoon guide (which, iirc, doesn't even go into the diagonal lemma, and just blends the Y combinator together with 1b).

this suggests that you're going to be hard-pressed to do any self-reference without routing through the nomal machinery of löb's theorem, in the same way that it's hard to do recursion in the lambda calculus without routing through the Y combinator--you don't need to use Y per se, but you're unlikely to find a simpler way to do generic recursion.

this also suggests that you're hiding all the work done by the normal proof of löb's theorem in the definition of "zip", and that this proof won't turn out to be simpler when "zip" is cashed out in full.

#2. fun fact: the diagonal lemma is also just an instance of the Y combinator with an extra level of quotation.

in fact, there's a proof of the diagonal lemma that goes by analogy to the proof-sketch of löb's theorem (above). very roughly speaking, the way that you avoid infinite regress is that, in the step 1a, you need an S with S ≃ □ S → Type, and this S can be written manually because Type (or Proposition or w/e you want to use) is very rich (namely, it contains existential quantifiers and equality).[3]

indeed, you can think of the diagonal lemma as simply an application of löb's theorem where the target A is Type (or Proposition or w/e).

in fact, this analogy is quite tight. one cool corollary is that we can pop open tarski's undefinability of truth, and replace the diagonal lemma with löb's theorem. the result is a new theorem that i call "the undefinability of normalization": no theory can prove that its terms normalize, on pain of contradiction.

(proof, in case it's not obvious: invoke löb's theorem on (not ∘ normalize : □ Bool → Bool), now you have syntax for a boolean value that's provably-equal to its own negation.)

#3. fun fact: löb's theorem does not hold for various breeds of normalized proofs (such as proofs with cuts eliminated--though exactly what counts as "normalized" in PA is somewhat subtle). in particular, when □ denotes normalized proofs, □(A → B) ∧ □(A) does not yield □(B), because feeding a normalized argument into a normalized function does not yield a normalized output. and while we (who trust the theory) know that unnormalized-box(B) implies normalized-box(B), no consistent theory can prove its own version of that fact, by the undefinability of normalization!

...which yields the hypothesis that the One True Counterfactuals are those facts which have short normalized proofs.

(recall: i think it was patrick who first set forth the trolljecture that counterfactuals correspond to short proofs of material implications? and this trolljecture was shot down by the existence of spurious counterfactuals, which use löb to deduce arbitrary material implications with a ~constant proof-length. but that counterexample doesn't apply to normalized proofs! so the repaired trolljecture yet stands!)

(though i admit this hasn't risen high enough in my priority-queue for me to actually try to prove nice things about this bold new notion of counterfactuals. also they obviously can't be the whole answer, b/c normalized proofs about large worlds are large, etc.)

  1. slighly more formally: both the Y combinator and löb's theorem are instantiations of a generalization of lawvere's fixpoint theorem to semicategories. in the case of the Y combinator, we use some domain (in the sense of domain theory) that serves as semantics for the untyped lambda calculus. in löb's theorem, iirc we use a semicategory where a morphism from A to B is a proof of □ A → B (tho this is an old cached thought that i haven't checked). that the latter is not a category follows from gödel incompleteness; there's no identity morphism at ⊥.

    note: i dislike semicategories, and if you have a more elegant way to unify Y and löb, i'm eager to hear it. ↩︎

  2. in other words: the santa clause sentence is just the natural/obvious type of the variable in the Y combinator (as modified to work with gödel-codes). if you want a better intuition for it, i recommend the exercise of trying to figure out what type the variable s should have in the normal Y combinator. ↩︎

  3. in fact, according to me, this is one of three keys to löb's theorem.

    the first two keys are ofc gödel-codes + the Y combinator, with the caveat that making the Y combinator behave requires the diagonal lemma.

    and the diagonal lemma is again just gödel-codes + the Y combinator, except that in this very specific case we can make the Y combinator behave without already needing the diagonal lemma, by hand-coding in a workaround using quantifiers and equalities and whatnot.

    and the hand-coded workaround is kinda hacky. very roughly speaking, the trouble is that we want to let G(s) be F (s "s"), but showing that s "s" is sensical relies on the diagonal lemma, which we're in the middle of proving and can't invoke.

    and the solution is to let G(s) instead be ∃ x. just x = try (s "s") ∧ F x. we don't need to know that s "s" is sensical, because we're naming a proposition, and we can just bolt on a clause asserting that s "s" is sensical! we just build our sentence to say "s "s" is sensical, and also ...", and thus sidestep the problem!

    in other words: we're able to build a sentence that would be meaningful (it would mean a falsehood) even if s "s" wasn't sensical, and this lets us form a sort of "guarded" version of the Y combinator (in the special case where we're producing a sentence) that doesn't depend critically on the sensicality of s "s". (which ends up making s "s" be sensical in the actual use-case of G "G", and so the guard ends up redundant and harmless.)

    (exercise: why can't you use this technique to avoid the invocation of the diagonal lemma from the proof of gödel's incompleteness theorem, i.e. löb's theorem where the target A is ⊥?)

    this technique lets us slip around the need to invoke the diagonal lemma before we've finished proving the diagonal lemma. which is a critical step in the bootstrapping process.

    ...i don't have this point entirely distilled yet, but hopefully that gives at least some intuition for what i mean when i say that löb is just gödel-codes + the Y combinator + a hacky workaround to get you off the ground. ↩︎

Reply
[-]So8res*Ω7130

an attempt to rescue what seems to me like the intuition in the OP:

(note that the result is underwhelming, but perhaps informative.)

in the lambda calculus we might say "given (f : A → A), we can get an element (a : A) by the equation (a := f a)".

recursive definitions such as this one work perfectly well, modulo the caveat that you need to have developed the Y combinator first so that you can ground out this new recursive syntax (assuming you don't want to add any new basic combinators).

by a directly analogous argument, we might wish define (löb f := f "löb f"). very direct! very quine-like!

and, this proof works perfectly well. ...modulo the caveat that you need to have developed a modified Y combinator first, so that you can ground out this recursive syntax (assuming you don't want to add any new axioms).

so if you prove the existence of a modified Y-combinator (that works w/ quotations), then you can add recursive syntax (modulo quotation) to your theory, and get a very "direct/quine-like" proof of löb's theorem.

the only hiccup is that the modified-Y-combinator is itself löb's theorem, so the above proof amounts to "once you have proven löb's theorem, there is a very direct and intuitive proof of löb's theorem", which... is perhaps less exciting :-p

(bonus fun fact: in type theory, there's an operator that forms quines. and the proof of löb's theorem is extremely simple, given this operator; you just take a (syntactic) term of type □ A → A, and feed it the quotation of the result of this whole operation, using the quining operator. the hiccup is, ofc, that the quining operator is itself just löb's theorem!)

Reply
[-]So8res*Ω9150

various attempts to distill my objection:

the details of the omitted "zip" operation are going to be no simpler than the standard proof of löb's theorem, and will probably turn out to be just a variation on the standard proof of löb's theorem (unless you can find a way of building self-reference that's shorter than the Y combinator (b/c the standard proof of löb's theorem is already just the Y combinator plus the minimal modifications to interplay with gödel-codes))

even more compressed: the normal proof of löb is contained in the thing labeled "zip". the argument in the OP is operating under the assumption that a proof can make reference to its own gödel-number, and that assumption is essentially just löb's theorem.

a thing that might help is asking what specific proof-steps the step "1. the gödel-code P of this very proof proves C" cashes out into. obviously step 1 can't cash out into verifying (under quotation) every step of the entire proof (by checking for the appropriate prime-factors), because then the proof would require at least one step for every step in the proof plus three extra steps at the end, which would make the proof infinite (and infinite proofs admit contradictions).

so step 1 has to involve some indirection somehow. (cf: we can't get a fixpoint in λ-calculus by f (f (f ..., we need some indirection, as occurs in (Y f) aka (λ s. f (s s)) (λ s. f (s s)), to make the term finite.)

this works fine, as long as you are ok w/ the gödel-code in step 1 being not P, but some different proof of the same conclusion (analogous to the difference between f (Y f) and Y f), and so long as you have the analog of the Y combinator (modified to interplay with gödel-codes).

but the analog of the Y combinator is precisely löb's theorem :-p

if i understand your OP correctly, we can factor it into three claims:

  1. when proving C, it's valid to assume a referece «this» to the gödel-code of a proof of C
  2. given (1) and a proof f of □ C → C, there's a proof of C by simply applying f to «this»
  3. you can arrange things such that if you desugar «this» into a particular numeral in "f «this»", you'll find that that numeral is the gödel-code of "f «this»".

(1) is löb's theorem.

(2) is an indirect proof of löb's theorem, from the assumption of löb's theorem (in direct analogy with how, once we've found syntax Y f for the fixpoint of f, we can wrap it in f to find an alternate syntax, namely f (Y f)).

(3) is false (i'm fairly confident)--you can get real close, but you can't quite get there (in direct analogy to how you can get λ-term Y f that means the same thing as f (Y f), but you can't get a λ-term fix f that is syntactically exactly f (fix f), on pain of infinite syntax).

afaict, there's two ways to read this proposal (if we port across the analogy to λ-calculus), according to whether you cash "zip" out to a recursive instance of the whole proposal, vs whether you cash "zip" out to some different proof of löb's theorem:

  1. "i hear that people find the Y combinator confusing. instead of using (Y f) to name the fixpoint of f, why not use f (f (f (f (... ad infinitum?"

  2. "i hear that people find the Y combinator confusing. instead of using (Y f) to name the fixpoint of f, why not use f (Y f)?"

the answer to (1) is that it doesn't make sense unless you allow infinite syntax trees (which aren't permitted in normal math b/c infinite proofs admit contradictions).

the answer to (2) is that, while (Y f) may be somewhat tricky to grasp, f (Y f) is surely no simpler :-p

Reply
[-]Amalthea10

I was interpreting things somewhat differently:

  1. "this" should be a reference to the Gödel code of the current proof
  2.  the OP would like to have what is essentially an application of the diagonal lemma to the whole  proof instead of a proposition
  3. "zip"/"unzip" is simply taking the Gödel numbering, and doesn't hide any extra complexity

In this case the problem here is making precise what one hopes for in step 2. (I don't really see how one would do it), and then to prove that one can make it work. 

Reply
[-]So8res30

part of my point is that the standard proof of löb does essentially apply the main idea of the diagonal lemma to the whole proof instead of to a proposition. when you look at the standard proof of löb from the right angle, it looks very similar to the standard standard proof of the diagonal lemma (namely, they both look like lawvere's fixpoint theorem, as does the Y combinator).

löb lets you define a proof by reference to its own gödel-code, just like how the diagonal lemma lets you define a proposition by reference to its own gödel-code. (the former just happens to recurse into the latter at one point along the way, as an implementation detail.)

("but wait, if the mechanisms are so similar, then why doesn't the diagonal lemma have to recurse into the diagonal lemma at one point along the way, as an implementation detail?" it almost does! and this almost sinks the ship! the diagonal lemma requires an extra hacky insight, that works only in the special case of the diagonal lemma, and that is required to get off the ground. i discuss this in footnote 2 of my original comment, iirc.)

another part of my point is that the hard part of zip/unzip isn't the part where you take the gödel-numbering, it's the part where you make the gödel-numbering of the proof you're currently naming available to the proof that you haven't finished defining yet. that's the tricky part of löb's theorem. if we ignore that part, it's no surprise that we find the remainder is simpler: we skipped the hard part!

Reply
[-]So8res20

(another thing that might help: when you're proving an implication □ C → C, the gödel-number that you're given doesn't code for the proof of the implication you're currently writing; that would be ill-typed. you asked for a □ C, not a □ (□ C → C). so the gödel-number you're given isn't a code for the thing you're currently writing, it's a code for löb's theorem applied to the thing you're currently writing.

it is for this reason that the proof you're fed might not be exactly the proof you were hoping for. you started out your implication being like "step 1: this proof is a proof of C", but then the proof that you're fed starts out saying "step 1: apply löb's theorem to the following implication", and only at step 2 is it like "this proof is a proof of C".

you might have really wanted the proof you're fed to start with "step 1: this proof is a proof of C". and you might say "well, inline the application of löb's theorem there, so that the code i'm fed codes for a proof that actually starts that way". this is like trying to get the fixpoint of f in the λ-calculus by way of f (f (f (...: you can do that for as many steps as you like, but you have to end at (Y f) at some point, on pain of infinite terms (which are contradictory in the mathematical setting).

alternatively, you might accept that the proof you're fed codes for a proof that starts by saying "apply löb's theorem to the following implication: ..."; this corresponds to being fed the term (Y f) and producing the term f (Y f).

in neither case does it seem to me like there's an idea for some alternative method of producing the self-reference, so as to sidestep the Y-combinator-esque machinery that makes up the bulk of the proof of löb's theorem (and that is the source of the recursive call into the diagonal lemma).)

Reply
[-]Andrew_CritchΩ250

this suggests that you're going to be hard-pressed to do any self-reference without routing through the nomal machinery of löb's theorem, in the same way that it's hard to do recursion in the lambda calculus without routing through the Y combinator

If by "the normal machinery", you mean a clever application of the diagonal lemma, then I agree.  But I think we can get away with not having the self-referential sentence, by using the same y-combinator-like diagonal-lemma machinery to make a proof that refers to itself (instead of a proof about sentences that refer to themselves) and checks its own validity.  I think I if or someone else produces a valid proof like that, skeptics of its value (of which you might be one; I'm not sure) will look at it and say "That was harder and less efficient than the usual way of proving Löb using the self-referential sentence  and no self-validation".  I predict I'll agree with that, and still find the new proof to be of additional intellectual value, for the following reason:

  • Human documents tend to refer to the themselves a lot, like bylaws.
  • Human sentences, on the other hand, rarely refer to themselves.  (This sentence is an exception, but there aren't a lot of naturally occurring examples.)
  • Therefore, a proof of Löb whose main use of self-references involves the entire proof referring to itself, rather than a sing sentence referring to itself, will be more intuitive to humans (such as lawyers) who are used to thinking about self-referential documents.

The skeptic response to that will be to say that those peoples' intuitions are the wrong way to think about y-combinator manipulation, and to that I'll be like "Maybe, but I'm not super convinced their perspective is wrong, and in any case I don't mind meeting them where they're at, using a proof that they find more intuitive.".

Summary: I'm pretty confident the proof will be valuable, even though I agree it will have to use much of the same machinery as the usual proof, plus some extra machinery for helping the proof to self-validate, as long as the proof doesn't use sentences that are basically only about their own meaning (the way the sentence  is basically only about its own relationship to the sentence C, which is weird).

Reply
[-]Ben PaceΩ8120

This sentence is an exception, but there aren't a lot of naturally occurring examples.

No strong claim either way, but as a datapoint I do somewhat often use the phrase "I hereby invite you to <event>" or "I hereby <request> something of you" to help move from 'describing the world' to 'issuing an invitation/command/etc'.

Reply
[-]Andrew_CritchΩ120

True!  "Hereby" covers a solid contingent of self-referential sentences.  I wonder if there's a "hereby" construction that would make the self-referential sentence Ψ (from the Wikipedia poof) more common-sense-meaningful to, say, lawyers.

Reply
[-]So8res*Ω120

which self-referential sentence are you trying to avoid?

it keeps sounding to me like you're saying "i want a λ-calculus combinator that produces the fixpoint of a given function f, but i don't want to use the Y combinator".

do you deny the alleged analogy between the normal proof of löb and the Y combinator? (hypothesis: maybe you see that the diagonal lemma is just the type-level Y combinator, but have not yet noticed that löb's theorem is the corresponding term-level Y combinator?)

if you follow the analogy, can you tell me what λ-term should come out when i put in f, and how it's better than (λ s. f (s s)) (λ s. f (s s))?

or (still assuming you follow the analogy): what sort of λ-term representing the fixpoint of f would constitute "referring to itself (instead of being a term about types that refer to themselves)"? in what sense is the term (λ s. f (s s)) (λ s. f (s s)) failing to "refer to itself", and what property are you hoping for instead?

(in case it helps with communication: when i try myself to answer these questions while staring at the OP, my best guess is that you're asking "instead of the Y combinator, can we get a combinator that goes like f ↦ f ????", and the two obvious ways to fill in the blanks are f ↦ f (Y f) and f ↦ f (f (f (.... i discussed why both of those are troublesome here, but am open to the possibility that i have not successfully understood what sort of fixpoint combinator you desire.)

(ETA: also, ftr, in the proof-sketch of löb's theorem that i gave above, the term "g "g"" occurs as a subterm if you do enough substitution, and it refers to the whole proof of löb's theorem. just like how, in the version of the Y combinator given above, the term g g occurs as a subterm if you do enough β-reduction, and it refers to the whole fixpoint. which i note b/c it seems to me that you might have misunderstood a separate point about where the OP struggles as implying that the normal proof isn't self-referring.)

((the OP is gonna struggle insofar as it does the analog of asking for a λ-term x that is literally syntactically identical to f x, for which the only solution is f (f (f (... which is problematic. but a λ-term y that β-reduces pretty quickly to f y is easy, and it's what the standard constuction produces.))

Reply
[-]Andrew_CritchΩ130

At this point I'm more interested in hashing out approaches that might actually conform to the motivation in the OP.  Perhaps I'll come back to this discussion with you after I've spent a lot more time in a mode of searching for a positive result that fits with my motivation here.  Meanwhile, thanks for thinking this over for a bit.

Reply
[-]So8res*Ω241

well, in your search for that positive result, i recommend spending some time searching for a critch!simplified alternative to the Y combinator :-p.

not every method of attaining self-reference in the λ-calculus will port over to logic (b/c in the logical setting lots of things need to be quoted), but the quotation sure isn't making the problem any easier. a solution to the OP would yield a novel self-reference combinator in the λ-calculus, and the latter might be easier to find (b/c you don't need to juggle quotes).

if you can lay bare the self-referential property that you're hoping for in the easier setting of λ-calculus, then perhaps others will have an easier time understanding what you want and helping out (and/or you'll have an easier time noticing why your desires are unsatisfiable).

(and if it's still not clear that löb's theorem is tightly connected to the Y combinator, such that any solution to the OP would immediately yield a critch!simplified self-reference combinator in the λ-calculus, then I recommend spending a little time studying the connection between the Y combinator, löb's theorem, and lawvere's fixpoint theorem.)

Reply
[-]Eliezer YudkowskyΩ6112

Forgive me if this is a dumb question, but if you don't use assumption 3: []([]C -> C) inside steps 1-2, wouldn't the hypothetical method prove 2: [][]C for any C?

Reply
[-]Andrew_CritchΩ5121

Thanks for your attention to this!  The happy face is the outer box.  So, line 3 of the cartoon proof is assumption 3.

If you want the full []([]C->C) to be inside a thought bubble, then just take every line of the cartoon and put into a thought bubble, and I think that will do what you want. 

LMK if this doesn't make sense; given the time you've spent thinking about this, you're probably my #1 target audience member for making the more intuitive proof (assuming it's possible, which I think it is).

ETA:  You might have been asking if there should be a copy of Line 3 of the cartoon proof inside Line 1 of the cartoon proof.  The goal is, yes, to basically to have a compressed copy of line 3 inside line 1, like how the strings inside this Java quine are basically a 2x compressed copy of the whole program:
https://en.wikipedia.org/wiki/Quine_(computing)#Constructive_quines#:~:text=java

The last four lines of the Java quine are essentially instructions for duplicating the strings in a form that reconstructs the whole program.  

If we end up with a compressed proof like this, you might complain that the compression is being depicted as magical/non-reductive, and ask for cartoon that breaks down into further detail showing how the Quinean  compression works.  However, I'll note that your cartoon guide did not break down the self-referential sentence L into a detailed cartoon form; you used natural language instead, and just illustrated vaguely that the sentence can unpack itself with this picture:

I would say the same picture could work for the proof, but with "sentence" replaced by "proof".

Reply
[-]Eliezer YudkowskyΩ340

Okay, that makes much more sense.  I initially read the diagram as saying that just lines 1 and 2 were in the box.

Reply
[-]AlexMennenΩ7128

It would kind of use assumption 3 inside step 1, but inside the syntax, rather than in the metalanguage. That is, step 1 involves checking that the number encoding "this proof" does in fact encode a proof of C. This can't be done if you never end up proving C.

One thing that might help make clear what's going on is that you can follow the same proof strategy, but replace "this proof" with "the usual proof of Lob's theorem", and get another valid proof of Lob's theorem, that goes like this: Suppose you can prove that []C->C, and let n be the number encoding a proof of C via the usual proof of Lob's theorem. Now we can prove C a different way like so:

  1. n encodes a proof of C.
  2. Therefore []C.
  3. By assumption, []C->C.
  4. Therefore C.

Step 1 can't be correctly made precise if it isn't true that n encodes a proof of C.

Reply
[-]Eliezer YudkowskyΩ81210

If that's how it works, it doesn't lead to a simplified cartoon guide for readers who'll notice missing steps or circular premises; they'd have to first walk through Lob's Theorem in order to follow this "simplified" proof of Lob's Theorem.

Reply
[-]Andrew_CritchΩ460

Yes to both of you on these points:

  • Yes to Alex that (I think) you can use an already-in-hand proof of Löb to make the self-referential proof work, and
  • Yes to Eliezer that that would be cheating wouldn't actually ground out all of the intuitions, because then the "santa clause"-like sentence is still in use in already-in-hand proof of Löb.

(I'll write a separate comment on Eliezer's original question.)

Reply
[-]GurkenglasΩ797

Similarly:

löb = □ (□ A → A) → □ A
□löb = □ (□ (□ A → A) → □ A)
□löb -> löb:
  löb premises □ (□ A → A).
  By internal necessitation, □ (□ (□ A → A)).
  By □löb, □ (□ A).
  By löb's premise, □ A.
Reply
[-]Andrew_CritchΩ120

Noice :)

Reply
[-]Gurkenglas20

When disambiguating as far as possible, löb becomes □(□B → A) → □A, but □löb becomes □(□(□B → A) → □B). Perhaps Ψ has a universal property related to this?

Reply
[-]ShmiΩ811-2

I know very little about this area, but I suspect that a writeup like this classic explanation of Godel Incompleteness might be a step in the right direction: Godel incompleteness.

Reply
[-]Andrew_CritchΩ140

That thing is hilarious and good!  Thanks for sharing it.  As for the relevance, it explains the statement of Gödel's theorem, but not the proof it.  So, it could be pretty straightforwardly reworked to explain the statement of Löb's theorem, but not so easily the proof of Löb's theorem.  With this post, I'm in the business of trying to find a proof of Löb that's really intuitive/simple, rather than just a statement of it that's intuitive/simple.

Reply
[-]davidadΩ490

Forgive me if I’m missing something but as far as I can tell, this line of inquiry was already pursued to its logical conclusion (namely, an Agda-verified quinean proof of Löb’s theorem) in this paper by Jason Gross, Jack Gallagher and Benya Fallenstein.

Reply
[-]Andrew_CritchΩ231

Thanks for raising this!  I assume you're talking about this part?

They explore a pretty interesting set-up, but they don't avoid the narrowly-self-referential sentence Ψ:

So, I don't think their motivation was the same as mine.  For me, the point of trying to use a quine is to try to get away from that sentence, to create a different perspective on the foundations for people that find that kind of sentence confusing, but who find self-referential documents less confusing.  I added a section "Further meta-motivation (added Nov 26)" about this in the OP.

Reply
[-]metachirality30Review for 2022 Review

This made me grok Löb's theorem enough to figure out how to exploit it for self-improvement purposes.

Reply
[-]Martín Soto20

Given you want to "push the diagonal lemma around / hide it somewhere" and come up with something equivalent but with another shape (I share Nate's intuitions), something like this paper's appendix (§12) might be useful: they build the diagonal lemma directly into the Gödel numbering. This might allow for defining your desired proof by a formula and trivially obtaining existence (and your target audience won't need to know weird stuff happened inside the Gödel numbering). I'll try to work this out in the near future.

Reply
[-]Victor Novikov10

Another try at understanding/explaining this, on an intuitive level.

Teacher: Look at Löb's theorem and its mathematical proof. What do you see?
Student: I don't really follow all the logic.
T: No. What do you see?
S: ...
A containment vessel for a nuclear bomb.
T: Yes. Why?
S: Because uncontained self-reference destroys any formal system?
T: Yes. 
How is this instance of self-reference contained?
S: It resolves only one way.
T: Explain how it resolves.
S: If a formal system can prove its own soundness, then any answer it gives is sound. As its soundness has already been proven.
T: Yes.
S: However in this case, it has only proven its soundness if the answer is answer is true. So the answer is true, within the system.
T: Yes. Can you explain this more formally?
S: The self-referential recipe for proving the soundness of the systems's own reasoning if the answer is true, necessarily contains the recipe for proving the answer is true, within the system.

Which isn't quite the same thing as understanding the formal mathematical proof of Löb's theorem, but I feel that (for now) with this explanation I understand the theorem intuitively.

Reply
[-]Amalthea10

I think I really don't see what the intuition behind the suggested strategy is. 

The standard proof of Löb's theorem as I understand it can be obtained by trying to formalize the paradoxical sentence "If this sentence is true, then C".  Intuitively, this sentence is clearly true, therefore C. (This of course doesn't work formally, what is missing is exactly the assumption that you can conclude C from a proof of C).

With your suggested proof, I just wouldn't believe it's a proof in the first place, so (for me) there's no reason to believe that it should work. If you can explain in more detail what exactly you would like to formalize, I would be curious. 

Reply
[-]Victor Novikov10

I have set out to fully and intuitely understand Löb's theorem.

I have found an answer that makes sense to my intuition. Not sure if it will come across, as I am a very non-neurotypical person who really thinks like a space alien sometimes.

Löb's theorem, the standard/explicit formulation (for reference)

(for any formula P)
If it is provable in PA that "if P is provable in PA then P is true", then P is provable in PA.

Löb's theorem, intuitive expression, version 2.0

If I am a provably logically coherent entity 
and I promise that "if I promise that you can trust me, then you can trust me", then you can trust me.

I am tentatively calling the concept "meta-trust". With that in mind, an even shorter formulation:

If you meta-trust me, then you trust me.

I'm not sure I can explain in explicit terms why my intuition feels this is true. I mean, it just seems obvious? But I can't explain yet why it is obvious.

And the correspondence between the two versions of the theorem is not 1:1. It uses somewhat different formulation/[type of concept]. It uses different kind of cognitive machinery. Even if it feels "obvious" to me that the statements are exactly equivalent.

Well, not exactly, because intuition never thinks in 100% exact terms. But it can think very exactly, just not infinitely so.

So, my question to you is:

Does this formulation make intuitive sense to you?
There are probably inference steps I have skipped. What are the inference steps that need to expanded on, to make the formulation more broadly understandable, without relying on some unspoken background knowledge?
And most importantly: if you this think that this formulation is logically incorrect, I would very much like to hear how it is incorrect.

Thank you for reading!

Reply
[-]kave10

What does "logically coherent" mean?

Reply
[-]Victor Novikov10

Good question!

I'm thinking sometime like, why do we trust PA?

It is because it is:

  • Logically consistent
  • Never lies (i. e. its outputs are the same as its conclusions)

And I'm thinking something like that, only in a person.
Well, it does't have to be a person, but my intuition prefers to think in terms of personhood.

"It is provable in PA that X is true" translates to "I am a logically coherent entity and I am telling you that X is true"

Reply
[-]kave10

What do you mean by "its outputs are the same as its conclusions"? If I had to guess I would translate it as "PA proves the same things as are true in every model of PA". Is that right?

Reply
[-]Victor Novikov10

No I just literally mean it cannot lie.

A human can hold one model of the world in his mind, but say something that fits with a different model of the world. A lie.

PA does not do that.

So I'm making it clear that I'm talking about entities like PA which do not (or cannot) lie.

Reply
[-]Kenku10

I have an objection towards the Troll Proof you linked in the picture. Namely, line 2 does not follow from line 1. □C states that “C is provable within the base system”, but the Troll Proof has “base system + □C→C” as its assumptions, per line 3.

The strongest statement we can get at line 2 is □((□C→C)→C), by implication introduction.

Reply
Moderation Log
More from Andrew_Critch
View more
Curated and popular this week
35Comments