What will GPT-4 be incapable of?
11Logan Zoellner
1Michaël Trazzi
5Alexei
3Michaël Trazzi
2ChristianKl
1Michaël Trazzi
6Danielle Ensign
4Ericf
1Michaël Trazzi
1Ericf
1Michaël Trazzi
1Ericf
1Michaël Trazzi
1Ericf
1Michaël Trazzi
3Zac Hatfield-Dodds
1Michaël Trazzi
1Zac Hatfield-Dodds
2Ericf
1Zac Hatfield-Dodds
1tailcalled
-9skybrian
13Michaël Trazzi
10niplav
11NunoSempere
11[anonymous]
7HDMI Cable
1Michaël Trazzi
2HDMI Cable
7hogwash9
4niplav
2Peter Wildeford
1Michaël Trazzi
New Answer
New Comment
6 Answers sorted by
110
Play Go better than AlphaGo Zero. AlphaGo Zero was trained using millions of games. Even if GPT-4 is trained on all of the internet, there simply isn't enough training data for it to have comparable effectiveness.
That's a good one. What would be a claim you would be less confident (less than 80%) about but still enough confident to bet $100 at 2:1 odds? For me it would be "gpt-4 would beat a random go bot 99% of the time (in 1000 games) given the right input of less than1000 bytes."
5
For me it would be: gpt4 would propose a legal next move to all 1000 random chess games.
3
Interesting. Apparently GPT-2 could make (up to?) 14 non-invalid moves. Also, this paper mentions a cross-entropy log-loss of 0.7 and make 10% of invalid moves after fine-tuning on 2.8M chess games. So maybe here data is the bottleneck, but assuming it's not, GPT-4's overall loss would be (NGPT−4/NGPT−2)0.076=(175/1.5)2∗0.016≈2x smaller than GPT-2 (cf. Fig1 on parameters), and with the strong assumption of the overall transfering directly to chess loss, and chess invalid move accuracy being inversely proportional to chess loss wins, then it would make 5% of invalid moves
2
It takes a human hundreds of hours to get to that level of play strength. Unless part of building GPT-4 involves letting it play various games against itself for practice I would be very surprised if GPT-4 could even beat an average Go bot (let's say one who plays at 5 kyu on KGS to be more specific) 50% of the time.
I would put the confidence for that at something like 95% and most of the remaining percent is about OpenAI doing weird things to make GPT-4 specifically good for the task.
1
sorry I meant a bot that played random move, not a randomly sampled go bot from KGS. agreed with GPT-4 not beating average go bot
60
Things that it can probably do sometimes, but will fail on some inputs:
- Factor numbers
- Solve NP-Complete or harder problems
- Execute code
There are other “tail end” tasks like this that should eventually become the hardest bits that optimization spends the most time on, once it manages to figure everything else out.
40
Know if it's reply to a prompt is actually useful.
Eg: prompt with "a helicopter is most efficient when ... "; "a helicopter is more efficient when"; and "helicopter efficiency can be improved by." GPT-4 will not be able to know which response is the best. Or even if any of the responses would actually move helicopter efficiency in the right direction.
So physics understanding.
How do you think it would perform on simpler question closer to its training dataset, like "we throw a ball from a 500m building with no wind, and the same ball but with wind, which one hits the floor earlier" (on average, after 1000 questions).$? If this still does not seem plausible, what is something you would bet $100 2:1 but not 1:1 that it would not be able to do?
1
What do you mean by "on average after 1000 questions"? Because that is the crux of my answer: GPT-4 won't be able to QA its own work for accuracy, or even relevance.
1
well if we're doing a bet then at some point we need to "resolve" the prediction. so we ask GPT-4 the same physics question 1000 times and then some humans judges count how many it got right, if it gets it right more than let's say 95% of the time (or any confidence interval) , then we would resolve this positively. of course you could do more than 1000, and with law of large numbers it should converge to the true probability of giving the right answer?
1
That wouldn't be useful, though.
My assertion is more like: After getting the content of elementary school science textbooks (or high school physics, or whatever other school science content makes sense), but not including the end-of-chapter questions (and especially not the answers), GPT-4 will be unable to provide the correct answer to more then 50% of the questions from the end of the chapters, constrained by having to take the first response that looks like a solution as it's "answer" and not throwing away more than 3 obviously gibberish or bullshit responses per question.
And that 50% number is based on giving it every question without discrimination. If we only count the synthesis questions (as opposed to the memory/definition questions), I predict 1%, but would bet on < 10%
1
let's say by concatenating your textbooks you get plenty of examples of f=m⋅a with "blablabla object sky blablabla gravity a=9.8m/s2 blablabla m=12kg blabla f=12∗9.8=120N. And then the exercise is: "blablabla object of mass blablabla thrown from the sky, what's the force? a) f=120 b) ... c) ... d) ...". then what you need to do is just do some prompt programming at the beginning by "for looping answer" and teaching it to return either a,b,c or d. Now, I don't see any reason why a neural net couldn't approximate linear functions of two variables. It just needs to map words like "derivative of speed", "acceleration", "d2z/dt2" to the same concept and then look at it with attention & multiply two digits.
1
Generally the answers aren't multiple choice. Here's a couple examples of questions from a 5th grade science textbook I found on Google:
1. How would you state your address in space. Explain your answer.
2. Would you weigh the same on the sun as you do on Earth. Explain your answer.
3. Why is it so difficult to design a real-scale model of the solar system?
1
If it's about explaining your answer with 5th grade gibberish then GPT-4 is THE solution for you! ;)
30
Reason about code.
Specifically, I've been trying to get GPT-3 to outperform the Hypothesis Ghostwriter in automatic generation of tests and specifications, without any success. I expect that GPT-4 will also underperform; but that it could outperform if fine-tuned on the problem.
If I knew where to get training data I'd like to try this with GPT-3 for that matter; I'm much more attached to the user experience of "hypothesis write mypackage generates good tests" than any particular implementation (modulo installation and other managable ops issues for novice users).
I think the general answer to testing seems AGI-complete in the sense that you should understand the edge-cases of a function (or correct output from "normal" input).
if we take the simplest testing case, let's say python using pytest, with a typed code, with some simple test for each type (eg. 0 and 1 for integers, empty/random strings, etc.) then you could show it examples on how to generate tests from function names... but then you could also just do it with reg-ex, so I guess with hypothesis.
so maybe the right question to ask is: what do you expect GPT-...
1
Testing in full generality is certainly AGI-complete (and a nice ingredient for recursive self-improvement!), but I think you're overestimating the difficulty of pattern-matching your way to decent tests. Chess used to be considered AGI-complete too; I'd guess testing is more like poetry+arithmetic in that if you can handle context, style, and some details it comes out pretty nicely.
I expect GPT-4 to be substantially better at this 'out of the box' due to
* the usual combination of larger, better at generalising, scaling laws, etc.
* super-linear performance gains on arithmetic-like tasks due to generalisation, with spillover to code-related tasks
* the extra github (and blog, etc) data is probably pretty helpful given steady adoption since ~2015 or so
----------------------------------------
Example outputs from Ghostwriter vs GPT-3:
$ hypothesis write gzip.compress
import gzip
from hypothesis import given, strategies as st
@given(compresslevel=st.just(9), data=st.nothing())
def test_roundtrip_compress_decompress(compresslevel, data):
value0 = gzip.compress(data=data, compresslevel=compresslevel)
value1 = gzip.decompress(data=value0)
assert data == value1, (data, value1)
while GPT-3 tends to produce examples like (first four that I generated just now):
@given(st.bytes(st.uuid4()))
def test(x):
expected = x
result = bytes(gzip(x))
assert bytes(result) == expected
@given(st.bytes())
def test_round_trip(xs):
compressed, uncompressed = gzip_and_unzip(xs)
assert is_equal(compressed, uncompressed)
@given(st.bytes("foobar"))
def test(xs):
assert gzip(xs) == xs
@given(st.bytes())
def test(xs):
zipped_xs = gzip(xs)
uncompressed_xs = zlib.decompress(zipped_xs)
assert zipped_xs == uncompressed_xs
So it's clearly 'getting the right idea', even without any fine-tuning at all, but not there yet. It's also a lot worse at this without a natural-language description of the test we want in the prompt:
This d
2
I object to the characterization that it is "getting the right idea." It seems to have latched on to "given a foo of bar" -> "@given(foo.bar)" and that "assert" should be used, but the rest is word salad, not code.
1
It's at least syntatically-valid word salad composed of relevant words, which is a substantial advance - and per Gwern, I'm very cautious about generalising from "the first few results from this prompt are bad" to "GPT can't X".
10
Directing a robot using motor actions and receiving camera data (translated into text I guess to not make it maximally unfair, but still) to make a cup of tea in a kitchen.
-90
It's vaporware, so it can do whatever you imagine. It's hard to constrain a project that doesn't exist, as far as we know.
A model relased on openai.com with "GPT" in the name before end of 2022. Could be either GPTX where X is a new name for GPT4, but should be an iteration over GPT-3 and should have at least 10x more parameters.
Rendering 10/27 comments, sorted by (show more) Click to highlight new comments since:
I'd be surprised if it could do 5 or 6-digit integer multiplication with >90% accuracy. I expect it to be pretty good at addition.
It would really depend on how many parameters the model has IMO, if the jump from GPT-3 to GPT-4 is something on the order of magnitude of 10-100x, then we could potentially see similar gains for multiplication. GPT-3 (175B) can do 2 digit multiplication with a ~50% accuracy, so 5-6 digits might be possible. It really depends on how well the model architecture of GPT scales in the future.
So from 2-digit substraction to 5-digit substraction it lost 90% accuracy, and scaling the model by ~10x gave a 3x improvement (from 10 to 30%) on two-digit multiplication. So assuming we get 3x more accuracy from each 10x increase and that 100% on two digit corresponds to ~10% on 5-digit, we would need something like 3 more scalings like "13B -> 175B", so about 400 trillion params.
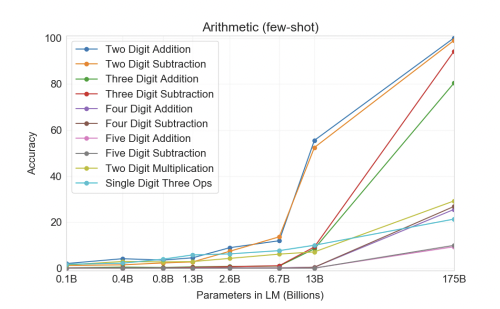
That's fair. Depending on your stance on Moore's Law or supercomputers, 400 trillion parameters might or might not be plausible (not really IMO). But, this is assuming that there's no advances in the model architecture (maybe changes to the tokenizer?) which would drastically improve the performance of multiplication / other types of math.
Going by GPT-2's BPEs [1], and based on the encoder downloaded via OpenAI's script, there are 819 (single) tokens/embeddings that uniquely map to the numbers from 0-1000, 907 when going up to 10,000, and 912 up to 200,000 [2]. These embeddings of course get preferentially fed into the model in order to maximize the number of characters in the context window and thereby leverage the statistical benefit of BPEs for language modeling. Which bears to mind that the above counts exclude numeric tokens that have a space at the beginning [3].
My point here being that, IIUC, for the language model to actually be able to manipulate individual digits, as well as pick up on the elementary operations of arithmetic (e.g. carry, shift, etc.), the expected number of unique tokens/embeddings might have to be limited to 10 – the base of the number system – when counting from 0 to the largest representable number [2].
[1] From the GPT-3 paper, it was noted:
This [GPT'3 performance on some other task] could be a weakness due to reusing the byte-level BPE tokenizer of GPT-2 which was developed for an almost entirely English training dataset.
[2] More speculatively, I think that this limitation makes extrapolation on certain abilities (arithmetic, algebra, coding) quite difficult without knowing whether its BPE will be optimized for the manipulation of individual digits/characters if need be, and that this limits the generalizability of studies such as GPT-3 not being able to do math.
[3] For such tokens, there are a total 505 up to 1000. Like the other byte pairs, these may have been automatically mapped based on the distribution of n-grams in some statistical sample (and so easily overlooked).
Hm, not so sure about this one anymore, since training on correct multiplication is easy using synthetic training data.
Seems like "the right prompt" is doing a lot of work here. How do we know if we have given it "the right prompt"?
Do you think GPT-4 could do my taxes?
re right prompt: GPT-3 has a context window of 2048 tokens, so this limits quite a lot what it could do. Also, it's not accurate at two-digit multiplication (what you would at least need to multiply your $ to %), even worse at 5-digit. So in this case, we're sure it can't do your taxes. And in the more general case, gwern wrote some debugging steps to check if the problem is GPT-3 or your prompt.
Now, for GPT-4, given they keep scaling the same way, it won't be possible to have accurate enough digit multiplication (like 4-5 digits, cf. this thread) but with three more scalings it should do it. Prompt would be "here is a few examples on how to do taxe multiplication and addition given my format, so please output result format", and concatenate those two. I'm happy to bet $1 1:1 on GPT-7 doing taxe multiplication to 90% accuracy (given only integer precision).
Curated and popular this week