This, in a nutshell, is why altruism exists in humans. It's limited and partial, but it solves the problem of cooperation by breaking the condition that everybody is solely looking after themselves.
Also, this is where acausal decision theories do very well at cooperation. Pretty much all the negative results on cooperation implicitly assume causal decision theory is being used.
Indeed, for acausal decision theories, identical copies cooperating is the case where it's easy to prove that they cooperate, which explains why the body has identical cells (And why the body suppresses foreign things so harshly).
Introduction to Non-Cooperative Game Theory
One of the most interesting applications of game theory and decision theory in general are the so-called “non-zero-sum games”. In these games, we have payoffs that do not cancel out between players, as in a zero-sum game, and it is possible to have intermediate payoffs.
More than that, these games are quite famous for working with the possibility of cooperation. In a zero-sum scenario, the rational action for players is always to maximize their payoff and reduce their rivals' results as much as possible (since a rival's gain necessarily means a loss for themselves). However, in a “non-zero-sum games” scenario, it is possible that players can cooperate because there is a chance that a gain for one of the players does not mean a loss for another.
Despite this, in general, the insights gleaned from these games are dismal. They show how agents acting in their own interest can generate deleterious and harmful results for a cooperative solution. The most famous of these games is the infamous Prisoners' Dilemma. This game, popularized by the Hollywood as a contest for girls, was developed in the 1950s by mathematicians Melvin Drescher and Alex Tucker at the Rand Corporation as a form of thought experiment to test hypotheses drawn from the work of Morgenstern and Von Neumann. Later, this game would be used as the perfect application of the idea of equillibrium developed by John Nash.
To illustrate this game let's use an ... fun example. I'm a big fan of british film director Christopher Nolan, mainly because of his extremely clever and complex plots. Nolan is the type of director who certainly spends a few hours reading Nature or Scientific American to improve his films.
One of his best movies is Batman: The Dark Knight. In this film, our eccentric billionaire hero is trying to save Gotham from a series of terrorist attacks carried out by his eternal rival, the Joker. In the final part of the film, Joker poses a wonderful dilemma (for the mathematicians who were watching, not for the characters in the film). There are two ships in Gotham's Bay, one with ordinary citizens and the other full of bandits. Both ships are filled with explosives and both have the ability to blow each other up. Joker gives each ship's crew a choice: If one blows up the other ship, the respective ship would be spared and, if neither used the detonator, both would blow up in the air.
If Joker's ship-exploding experiment were translated in terms of payoffs we would have:
◉ 1 = Survive;
◉ 0 = Die.
Citizens and bandits could choose between possible outcomes:
◉ [0,0] — Nobody triggers the detonator and Joker blows up both ships;
◉ [1,0] — Citizens trigger the detonator. Bad guys die and they live;
◉ [0,1] — The bandits trigger the detonator. Citizens die and they live.
If we organize the game in its strategic form we have the following scenario:
What would be the best decision to make in this scenario? A simple analysis reveals the answer. From the citizens' point of view, if they choose to cooperate with the bandits and don't trigger the detonator, they both die. But if they choose not to trigger and the bandits trigger theirs, the citizens die and the bandits live. And if they choose to trigger the detonator and the bandits choose to cooperate, the citizens survive and the they die. So, from the citizens' point of view, the best strategy is to trigger the detonator. Since the strategies are symmetric for citizens and bandits, this is also the best solution for bandits. Thus, the rational solution to Joker's game would be one in which both ships choose to detonate each other. In terms of game theory, this would be the game's Nash equilibrium and its dominant strategy with the following scenarios:
◉ I - Citizens (detonate) ; Bandits (detonate) - Payoff= [0,0]
◉ II - Citizens (detonate) ; Bandits (cooperate) - Payoff= [1,0]
◉ III - Citizens (cooperate); Bandits (detonate) - Payoff= [0,1]
◉ IV - Citizens (cooperate); Bandits (cooperate) - Payoff [0,0]
This is the Prisoners' Dilemma: a game that is not zero-sum, but whose best possible rational strategy is to betray the other player and not cooperate. What is most frightening about the outcome of the Prisoners' Dilemma is its implications. What the game tells us is that, when pursuing self-interest, individuals can sometimes generate outcomes whose rational choice has a consequence that is Pareto-inferior to other possible solutions. In this Hobbesian scenario, individuals would always be immersed in a state of wild competition whose only result would be the annihilation of all by all. Cooperation would not be a rational option, so it would always be necessary for an external agent (such as the State) to intervene to prevent the deleterious results that the balance of this game would bring.
Nozick's Critique of Rational Choice Theory
The Prisoners' Dilemma makes us believe that the rational choice of agents is always to betray each other in a non-cooperative outcome. However, not everyone agreed with this conclusion and some claimed that the rational choice of cooperation would actually be possible. Among those who disputed the results of the Prisoners' Dilemma is Robert Nozick.
Nozick is best known for his political philosophy, particularly his treatise on the theory of justice “Anarchy, State and Utopia”, yet few people know his 1993 treatise on the theory of knowledge “The Nature of Rationality”. In fact, Nozick's work can only be properly understood from its epistemology.
In his early years as a philosopher, Nozick learns from Carl Hempel, a neopositivist of the last generation of the Vienna Circle, the concept of “scientific explanation” as an alternative to “scientific argument”. While argumentation sought to establish logical formalizations capable of generating a definitive conclusion for a question, explanation sought to generate open and non-definitive linguistic formulations that would allow encompassing several critical perspectives for the same question. It is this concept, reformulated in a pluralist and evolutionary epistemological framework, which will be the cornerstone of Nozick's thought; this understood as a form of post-analytic philosophy.
This pluralist and critical perspective of utilitarian worldviews is what led him to formulate both his libertarian political treatise [1]and his critique of the results of the Prisoners' Dilemma. Nozick begins by pointing out that utility theory is insufficient to explain the various forms of human action [2]. The utility theory in question is that the value of an action would be given by the weighted sum of the causal and evidential utilities of a choice; with both being forms of expected utility. For him, an analysis of human action should include the symbolic utility of a given action in the sum of total utilities [3].
Symbolic utility is a concept that Nozick develops to express the utility that would be generated by performing an act and not by the results of the same act. It would originate from the symbolization of a certain action and not from the symbolized object; in such a way that it would be conditional, and could only be given in reason of the reasons for carrying such act. Unlike evidential and causal utilities, it is not a form of expected utility, as there are no probabilities involved in its determination.
Nozick then considers a game scenario where agents are not completely sure about the behavior of other agents and where, consequently, there is a variation in payoffs. This is the base scenario of the Prisoner's Dilemma that we were working on. In this scenario, what would happen if one of the sides, Bandits and Citizens, had a utility given by the act of cooperating? What would happen if one side valued doing “the right thing?” a little more than just surviving. The obvious solution would be to add this "extra" utility to our analysis of the game between Bandits and Citizens:
However, there is an error in trying to solve the Prisoners' Dilemma in this way. As Jerry Gaus points out, the mere addition of utility to one of the payoffs in the game matrix makes the Prisoners' Dilemma an entirely different game. That is, we change our original object of analysis. The above game is not a Prisoners Dilemma, but a Stag Hunt's game.
Stag Hunt was developed by the swiss philosopher Jean-Jacques Rousseau in his “Discourses” as a way of analyzing human nature [4]. In the example we have a simple case of hunting: No hunter can capture a stag and carry it alone, so cooperation between hunters is a necessary condition to achieve this result. However, the same hunter can hunt individual rabbits; with his bounty being less than the stag. A dilemma is formed in the sense that, if everyone remains at their post, everyone takes the highest prize of the deer and if at least one hunter leaves the post to hunt rabbits then it is best for everyone to hunt too to guarantee their hunt, abandoning the deer .
Rousseau expresses it this way:
"If it were a question of hunting a stag, everyone would realize that he must remain firmly at his post, but if a rabbit happened to pass within his reach, we cannot assure you that he would not run after it without any scruple, and, having obtained his prey , would care little if he caused his companions to lose theirs”
Thus, in a game of Stag Hunt we have two possible equilibria: Hunting the stag or hunting the rabbits. If the two hunters stay in their positions, they both win the bigger prize of the big red deer, if one goes after the rabbits then one wins and the other gets nothing and if they both go after the rabbits they will get the smaller prizes than if they had cooperated to capture the deer. Both equilibria are possible, but given the variance of the outcome if at least one of them is hunting rabbits, the rational choice is to hunt rabbits as it is less risky. The same happens with our case represented above. A game solution points out that there are two possible solutions ( [Cooperate; Cooperate] and [Detonate; Detonate] ), but the solution [Detonate ; Detonate ] is less risky given the payoff variance.
Solving a Stag game usually involves making pre-game rules to make the equillibrium [Cooperate ; Cooperate ] more attractive to players. That is, the players, before starting the game, carry out a communicative action in order to establish a system of rewards and punishments for the hunt. Thus, if punishments are established for the possibility of a hunter betraying others and going hunting for rabbits (such as having to share his reward with others), cooperation becomes the agents' rational strategy. This strategy is Rawls's solution to the problem of social order at the opening of "A Theory of Justice" [5]:
“A society is in order not only when the will to develop what is desirable for its members has been established, but also when it is effectively regulated by a public concept of justice. That is, to the extent that, first, each accepts and knows that others also accept the same principles of justice and, second, that basic social institutions satisfy these principles and are known as such"
So could we point out that Nozick's solution to the Prisoners' Dilemma is flawed, given that it actually transforms the original game into an entirely different one? The answer is no.
Nozick did not argue that the solution to the Prisoners' Dilemma would be given by simply adding utility to the game matrix. The reason for this is that symbolic utility could not be given as a simple benefit of an action. As previously mentioned, it arises from the symbolization of a certain action and not from its object; so that its value arises from the way the action is taken and not as a consequence of that action. Thus, Nozick argues that such utility could not be captured by the strategic game matrix, but only by the decisions taken in the game matrix:
"It might be thought that if an action does have symbolic utility, then this will show itself completely in the utility entries in the matrix for that action (for example, perhaps each of the entries gets raised by a certain fixed amount that stands for the act’s symbolic utility), so that there need not be any separate factor. Yet the symbolic value of an act is not determined solely by that act. The act’s meaning can depend upon what other acts are available with what payoffs and what acts also are available to the other party or parties. What the act symbolizes is something it symbolizes when done in that particular situation, in preference to those particular alternatives. If an act symbolizes “being a cooperative person,” it will have that meaning not simply because it has the two possible payoffs it does but also because it occupies a particular position within the two-person matrix (...) Hence, its symbolic utility is not a function of those features captured by treating that act in isolation, simply as a mapping of states onto consequences"
By stating that the symbolic utility could only be expressed by the decision process and not by the results, Nozick ends up delimiting that the symbolic utility could not be captured by the strategic form of a game (matrix), but only by its extensive form.
The extensive form of a game differs from the strategic form by presenting dimensions not captured by the strategic form. These forms are:
— Order: the order in which players make their moves matters for the analysis and outcome of the game;
— Alternatives: there may be different information available about the behavior of other players;
— Replay: The game can be played once or repeated infinitely or N times.
If we express the Stag Hunt game in an extensive form we would have the following representation:
If we try to solve this extensive game through the usual Subgame Perfect Nash Equilibrium method we would have the answer already given that the rational choice would be either to cooperate or to betray the other player given that the variance of the result would be fatal for one of them:
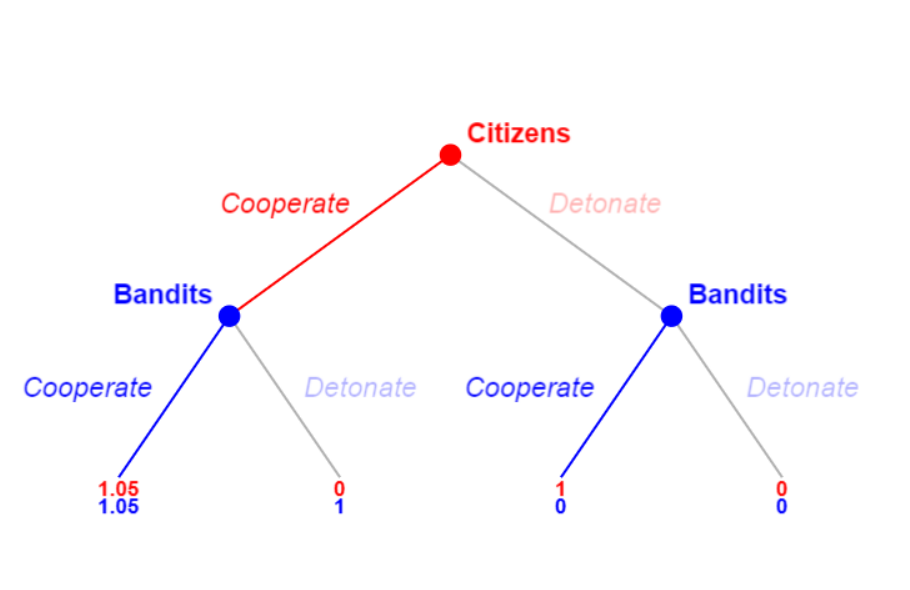
However, the extensive form of the Prisoners' Dilemma, despite seeming similar to the representation of the Stag Hunt, presents a fundamental difference. In a Prisoners' Dilemma game, there is the aforementioned condition that the agents "are not completely sure about the behavior of the other agent". That is, the agents are isolated and in total information asymmetry in relation to what the other is doing. In the extensive representation, it is as if the players each played separate, sequential games. To represent this information asymmetry, an “information set” is used to isolate the players' actions in extensive form. The representation of the first Prisoners' Dilemma and Nozick's modification would look like this in extensive form:
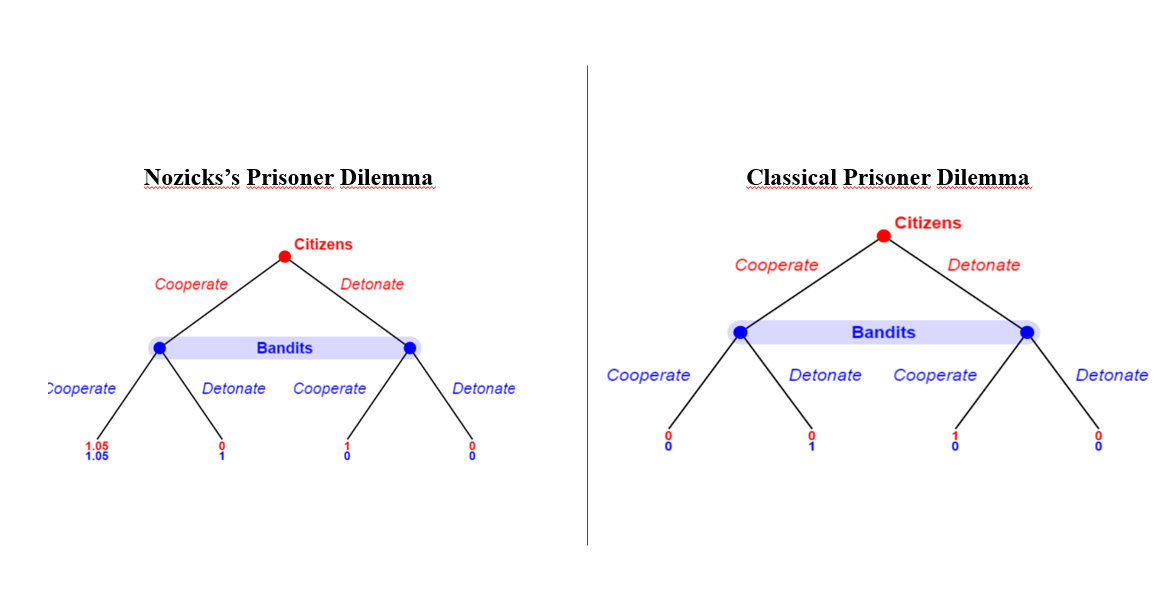
Apparently nothing has changed, we just added the “blue bar” that represents the game's information set. However, the difference is total [6]. If we solve the classic representation of the Prisoners' Dilemma we will have the first result, but if we solve the Nozickian representation we will have that there are only two possible equilibria [7]:
◉ Citizens (Cooperate); Bandits (Cooperate) - Payoff [1.05;1.05]
◉ Citizens (Detonate) ; Bandits (Detonate) - Payoff [0;0]
In this way, Nozick demonstrates that, in the portrayed scenario where the choice process can generate a symbolic utility, the rational choice would be to cooperate with the other agent even without communication and without game rules. The interesting thing is that this is exactly what happens in Batman. Neither the citizens nor the bandits choose to blow each other up as the rational choice would be (lucky for both of them the Dark Knight defeats the Joker before he blows up the ships too). This may demonstrate that both valued the symbolization of the act of cooperating in such a situation, either for ethical reasons or to signal to others that they were just people worthy of cooperation.
Nozick draws the most deontological conclusion possible from this, clearly:
"These considerations show that in situations like the Prisoners' Dilemma an action should be conceived as having utility by its own"
Thus, under the condition that there is a symbolic utility in the act itself, it may be rational for the agent not to follow the utilitarian choice of the Prisoners' Dilemma of not cooperating with the other agents.
The enlightened observer will have noticed that Nozick's results are strangely similar to the results of Kreps, Milgrom, Roberts and Wilson in their famous article "Rational Cooperation in the Finitely Repeated Prisioner's Dilemma" [8].
Criticisms and Implications
Nozick's conclusions obviously did not entirely convince everyone. Jerry Gaus rightly jokes that what Nozick did was actually create a "super complicated" form of the Stag Hunt game. The attentive observer will notice that the solutions are similar. The biggest criticism that can be raised against Nozick's solution, as noted by Gaus, is that it is minimally contestable to say that there is utility that is not captured in the game's payoffs. It is a principle of game theory that all relevant utilities for a player will be represented in the player's payoff, so that, if the person extracts utility from the act itself, then the utility cannot be "flying around" and not be expressed in the result of the same game.
Despite this criticism, Nozick's contribution with his theory of symbolic utility still seems quite plausible and has its pragmatic value in helping us to explain certain social phenomena.
An example that can be given is that Nozick's perspective helps to explain the electoral phenomenon in modern democracies. In an election, the probability of a vote changing the general result is basically zero, so that the benefit of voting is outweighed by the cost of participating in the same election (commuting to the polling place, waiting in line, etc). Since the expected benefit is zero and the marginal cost of voting is positive, the utility generated from the act of voting would theoretically be negative. Therefore, from the point of view of utility theory, it would be totally irrational for a person to leave home to vote.
However, even in electoral systems where voting is optional, people leave their homes to vote. Most people see value in participating in the democratic process and being embedded in political groups even if their vote brings no marginal benefit to the election. This need to express an identity through participation, to be part of a group, is an essential element of collective action and differs from the need for results taken as central in utilitarian decision theories, such as game theory.
Nozick's theory of symbolic utility helps us understand phenomena like this. People derive utility not from the outcome of the election but from the process of participating in it. It doesn't matter if the intended candidate will win or lose the election, people will still vote only for the symbolization of participating in the democratic process or to be inserted in a group with the same political affinities.
Nozick's theory also helps to explain certain problems of rational choice theory in explaining phenomena of ethical action. Let's look at a practical example for illustration. Suppose you are going to apply an entrance exam for two groups of people A and B. The exams of this entrance exam are marked with two colors, white and blue. You know that one of these two sets of tests is easier than the other, so that will give one of the two groups an advantage, and that group A has already received all the white tests in its chairs. So, what you do? Most people would answer that it would be fair to distribute all the blue tests to group B in order to increase the probability that they will receive the easier test and increase their advantages.
However, you discover the information that the easiest test is the blue one. So, what you do? Most people would answer, "I would reallocate the tests so that group B gets half of the blue tests and group A gets the other half." That would be the fair choice according to your vision. However, from a rational choice and game theory point of view, you have just violated the principle of dynamic consistency. The reason you allocated all the blue trials to B ex ante was that the probability of each group having the easiest trial was 50%. However, after you revise your choice given the information that the easiest race would be blue, the ex ante probability that A wins is 75%. There is a 50% probability that he will win in the initial situation and a 25% probability after his pick review.
From a utilitarian point of view your choice would be inconsistent and should be corrected by noting that your ex post choices might change in light of new information. Thus, the utilitarian agent would choose to adopt a commitment rule that prevents him from adopting a review of his ex ante choices at an ex post moment and thus generate a dynamic inconsistency [9]. However, what recent surveys show is that most people prefer to adopt a deontological stance of changing the distribution in the light of new information in order to maintain a rule of distributive justice ex post to the detriment of the dynamic consistency of their choices. Thus, most people adopt, even if tacitly, a deontological behavior as a choice because they see value in maintaining ethical principles (even if tacitly).
The implications of this are diverse. The main one is that human beings can choose to maintain principles of universal conduct over the utilitarian rationality of their actions. This may sound very nice…but it's not. In the case of privatization policies, for example, a technocrat or a politician may design the program so that the state-owned enterprise or “public good” is sold at its current market price plus discounts from expected future valuations. However, after privatization, the company or public good values more than expected and generates extraordinary profits. In this case, public policy makers may be tempted, under the justification of seeking ex post distributive justice, to reverse part of the privatization process or tax the gains of the privatized company or asset.
Therefore, given that people have forms of symbolic utility and can act inconsistently for deontological reasons, it is interesting to replace human agents in decision-making by agents that make their choices in accordance with the rationality rules of the theory. of the utilitarian decision; as forms of Artificial Intelligence.
A curiosity is that Nozick in his interviews always said that his philosophy had been more influenced by Hindu thought than American libertarian thought.
In fact, Nozick in a previous article was the first person to apply the theories of evidential and causal utility to the Newcomb Problem (which he himself elaborated) to show that the basic principles of both theories are inconsistent for a rational solution.
A formalization would say that the action value (AV) of a act X would be given by:
VA(X) = βUC(A) + βUE(A) + βUS(A)
Where β are the weights of a given utility, UC is the measure of causal utility, UE is the measure of evidential utility, and US is the measure of symbolic utility.
Several other philosophers have used the example of hunting games as thought experiments in the analysis of human nature; notably David Hume in his "Treatise on Human Nature". Adam Smith, in the opening of “Wealth of Nations”, uses a modified version of the game, replacing the hunters with greyhounds, to illustrate how economic cooperation would be an exclusively human characteristic in theory.
I would argue that the very dilemma between individual freedom and social welfare outlined in “A Theory of Justice” is the product of a Stag Hunt dilemma. Rawls defines justice as the collective fruit of individual choices in an “original position” and assumes that, because they are highly risk averse, they will sacrifice individual freedom in favor of social security.
The first difference is that asymmetric information games, such as the Prisoners' Dilemma, cannot be solved by Subgame Perfect Nash Equilibrium in extensive form.
In fact, there is a third solution which would be the use of mixed strategies. But that's beside the point in a game like the one we're analyzing.
In fact, Nozick even quotes this article in “The Nature of Rationality”, but claims that his explanation is different from that of the authors, as they consider the solution via finite sequential games and using the theory of expected utility under the hypothesis of rationality imperfect. According to Nozick, through the assumption that agents maximize the decision value in a normative way (as in the symbolic utility solution), then the authors' result could be maintained even under the assumption of perfect rationality.
See Elster (2000).