LESSWRONG
LW

Comment Permalink
conchis00

I agree with the substance of everything you have just said, and maintain that the only real point on which we disagree is whether the standard technical usage of "utility function" allows the choice set to be considered as part of the state description.

Anything else you want to include, go for it. But I maintain that, while it is clearly formally possible to include the choice set in in the state description, this is not part of standard usage, and therefore, your objection to Cyan's original comment (which is a well-established result based on the standard usage) was misplaced.

I have no substantive problem in principle with including choice sets in the state description; maybe the broader definition of "utility function" that encompasses this is even a "better" definition.

ETA: The last sentence of this comment previously said something like "but I'm not sure what you gain by doing so". I thought I had managed to edit it before anyone would have seen it, but it looks like Tim's response below was to that earlier version.

ETA2: On further reflection, I think it's the standard definition of transitive in this context that excludes the choice set from the state description, not the definition of utility function. Which I think basically gets me to where Cyan was some time ago.

Reply
timtyler00

You get to model humans with a utility function for one thing. Modelling human behaviour is a big part of point of utilitarian models - and human decisions really do depend on the range choices they are given in a weird way that can't be captured without this information.

Also, the formulation is neater. You get to write u(state) - instead of u(state - minus a bunch of things which are to be ignored).

Reply
See in context
by Peter_de_Blanc
2 min read
99

42

Unofficial Followup to: Fake Selfishness, Post Your Utility Function

A perception-determined utility function is one which is determined only by the perceptual signals your mind receives from the world; for instance, pleasure minus pain. A noninstance would be number of living humans. There's an argument in favor of perception-determined utility functions which goes like this: clearly, the state of your mind screens off the state of the outside world from your decisions. Therefore, the argument to your utility function is not a world-state, but a mind-state, and so, when choosing between outcomes, you can only judge between anticipated experiences, and not external consequences. If one says, "I would willingly die to save the lives of others," the other replies, "that is only because you anticipate great satisfaction in the moments before death - enough satisfaction to outweigh the rest of your life put together."

Let's call this dogma perceptually determined utility. PDU can be criticized on both descriptive and prescriptive grounds. On descriptive grounds, we may observe that it is psychologically unrealistic for a human to experience a lifetime's worth of satisfaction in a few moments. (I don't have a good reference for this, but) I suspect that our brains count pain and joy in something like unary, rather than using a place-value system, so it is not possible to count very high.

The argument I've outlined for PDU is prescriptive, however, so I'd like to refute it on such grounds. To see what's wrong with the argument, let's look at some diagrams. Here's a picture of you doing an expected utility calculation - using a perception-determined utility function such as pleasure minus pain.

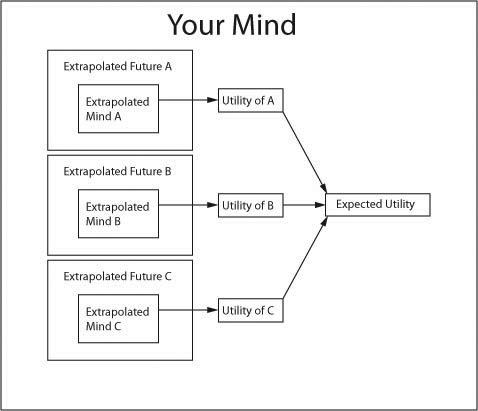
Here's what's happening: you extrapolate several (preferably all) possible futures that can result from a given plan. In each possible future, you extrapolate what would happen to you personally, and calculate the pleasure minus pain you would experience. You call this the utility of that future. Then you take a weighted average of the utilities of each future — the weights are probabilities. In this way you calculate the expected utility of your plan.

But this isn't the most general possible way to calculate utilities.

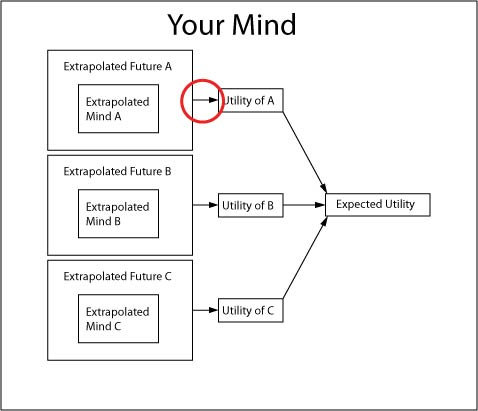
Instead, we could calculate utilities based on any properties of the extrapolated futures — anything at all, such as how many people there are, how many of those people have ice cream cones, etc. Our preferences over lotteries will be consistent with the Von Neumann-Morgenstern axioms. The basic error of PDU is to confuse the big box (labeled "your mind") with the tiny boxes labeled "Extrapolated Mind A," and so on. The inputs to your utility calculation exist inside your mind, but that does not mean they have to come from your extrapolated future mind.

So that's it! You're free to care about family, friends, humanity, fluffy animals, and all the wonderful things in the universe, and decision theory won't try to stop you — in fact, it will help.

Edit: Changed "PD" to "PDU."

Utility FunctionsWorld Modeling
Personal Blog

42

Mentioned in
Load More (5/13)
The Domain of Your Utility Function
New Comment
99 comments, sorted by
top scoring
Click to highlight new comments since:
Some comments are truncated due to high volume. (⌘F to expand all)Change truncation settings
[-]dclayh150

A mild defense of PDU:

If one says, "I would willingly die to save the lives of others," the other replies, "that is only because you anticipate great satisfaction in the moments before death - enough satisfaction to outweigh the rest of your life put together."

The other could also reply: "You say now that you would die because it gives you pleasure now to think of yourself as the sort of person who would die to save others. Moreover, if you do someday actually sacrifice yourself for others, it would be because the disutility of shattering your self-perception would seem to outweigh (in that moment) the disutility of dying."

(And now we have come back yet again to Newcomb, it seems.)

Reply
6A1987dM
"Would you kill someone for $100, if after killing them I could drug/hypnotize you so that you won't remember, and you'll never be able to find out?" You'd likely answer "yes" if your utility function is PD and "no" otherwise.
2wedrifid
It is a rare person indeed who would answer 'yes' to that question (without being frivolous). It implies valuing signalling honesty more than signalling not-planning-to-kill-folks. MoR!Quirrel might, depending on who he was talking to.
3TheOtherDave
I know a lot of people who I expect would answer 'yes' for a hundred thousand dollars when talking to me -- maybe with a "depends on the person" caveat. A few for $1000. But $100? Yeah, not very many. I suspect that threshold has more to do with the average level of wealth of my cohort than with our willingness to signal honesty.
6wedrifid
A hundred thousand is a lot of money! I deserve lots of trite costless signalling points for saying I wouldn't accept that offer. I'm holding out for a mil. Or at least a half! ;)
0[anonymous]
I would simply not trust the person making the offer for 100$. How do they make the consequences go away? Surely that costs at least a few thousand, assuming we're in a stable country. So why pay me so little? Besides the risk though, I don't see why murder should be expensive. It's not exactly complicated, assuming an unsuspecting civilian target. 100$ seems like a reasonable sum for the amount of work.
1Ben Pace
I don't know that MoR!Quirrell would care about the memory wipe at all. Money is money.
0A1987dM
I hadn't considered the possibility of lying. Make that “You likely would do that if ..., and you likely wouldn't otherwise.” Also, the amount of money and/or the number of people killed can be raised as needed for rich people/people who could kill one person for money anyway.
3wedrifid
(I would also usually specify "and there are no other consequences to you" as well given that most of the reason not to kill people is practical.)
0MineCanary
Or perhaps the pain of being a survivor when other's didn't and when you could have saved them (which can have an ongoing effect for the rest of your life) would outweigh the pleasure you could experience as a person living with survivor's guilt. Although, if you were rational, you could probably overcome the survivor's guilt, but still. I think in actual humans, if you were using this model as a metaphor for how they think, you'd have to say they sometimes irrational perceive another's brain as their own, so they're counting the net pleasure of the people they save in the utility calculation for their future mind. After all, throughout the past they've been able to derive pleasure from other people's pleasure or from imagining it, and it takes rational thought to eliminate that component from the calculation upon realizing that their brain will no longer be able to feel.
[-]TsviBT60

A counterexample to the claim "psychologically normal humans (implicitly) have a utility function that looks something like a PDU function":

Your best friend is deathly ill. I give you a choice between Pill A and Pill B.

If you choose Pill A and have your friend swallow it, he will heal - but he will release a pheromone that will leave you convinced for the rest of your life that he died (and you won't interact with him ever again).

If you choose Pill B and swallow it, your friend will die - but you will be convinced for the rest of your life that... (read more)

Reply
0[anonymous]
If I can't distinguish my hallucinations from the real person, then as per the Generalized Anti-Zombie Principle the hallucinations are just as sapient as himself.
0wedrifid
0A1987dM
How did you do that? There was no reply to that comment when I reloaded the page after retracting it in order to delete it. Are you a ninja or something? :-)
6wedrifid
Worse, a multitasker. That kind of things wreaks havoc on race conditions. I've removed my reply and the associated quote.
0A1987dM
I know... Minutes ago I lost a hand in an online poker game (with fake money, fortunately) as a result of being talking to someone else at the same time for the umpteenth time. And I've removed the parenthetical in my reply to you.
4ArisKatsaris
One probably just needs to keep open the browser tab from a time when your post had not yet been deleted...
[-]Scott Alexander60

I don't think this post adequately distinguishes between two concepts: how does the human utility function actually work, and how should it work.

The answer to the first question is (I thought people here agreed) that humans weren't actually utility maximizers; this makes things like your descriptive argument against perceptive determinism unnecessary and a lot of your wording misleading.

The second question is: if we're making some artificial utility function for an AI or just to prove a philosophical point, how should that work - and I think your answer is... (read more)

Reply
4Wei Dai
Where I've seen people use PDUs in AI or philosophy, they weren't confused, but rather chose to make the assumption of perception-determined utility functions (or even more restrictive assumptions) in order to prove some theorems. See these examples: * http://www.hutter1.net/ai/ * http://www.spaceandgames.com/?p=22 Here's a non-example, where the author managed to prove theorems without the PDU assumption: * http://www.idsia.ch/~juergen/goedelmachine.html
3Wei Dai
I wrote earlier: Well, here's a recent SIAI paper that uses perception-determined utility functions, but apparently not in order to prove theorems (since the paper contains no theorems). The author was advised by Peter de Blanc, who two years ago wrote the OP arguing against PDUs. Which makes me confused: does the author (Daniel Dewey) really think that PDUs are a good idea, and does Peter now agree?
0Peter_de_Blanc
I don't think that human values are well described by a PDU. I remember Daniel talking about a hidden reward tape at one point, but I guess that didn't make it into this paper.
0timtyler
An adult agent has access to its internal state and its perceptions. If we model its access to its internal state as via internal sensors, then sense data are all it has access too - its only way of knowing about the world outside of its genetic heritage. In that case, utility functions can only accept sense data as inputs - since that is the only thing that any agent ever has access to. If you have a world-determined utility function, then - at some stage - the state of the world would first need to be reconstructed from perceptions before the function could be applied. That makes the world-determined utility functions an agent can calculate into a subset of perception-determined ones.
4thomblake
Agreed. This post seems to add little to the discourse. However, it's useful to write clear, concise posts to sum these things up from time to time. With pictures!
0pjeby
Spot on for what, precisely? If one's goal is to make an AI that mirrors human values, it would not be every useful for it to use an utterly alien model of thought like utility maximization. ISTM that superhuman AI is the one place where you can't afford to use wishful thinking models in place of understanding what humans really do, and how they'll really act.
6Vladimir_Nesov
To model how humans really work, the AI needs to study real humans, not be a real human. The best bridge engineers are not themselves bridges. (Maybe I completely misunderstood what you wrote, in which case please correct me, but it looks like you're suggesting that AIs that mirror human values must be implemented in the way humans really work.)
0pjeby
I'm saying that a system that's based on utility maximizing is likely too alien of a creature to be able to be safely understood and utilized by humans. That's more or less the premise of FAI, is it not? Any strictly-maximizing agent is bloody dangerous to anything that isn't maximizing the same thing. What's more, humans are ill-equipped to even grok this danger, let alone handle it safely.
3Vladimir_Nesov
The best bridges are not humans either.
-7pjeby
-1timtyler
Utility maximization can model any goal-oriented creature, within reason. Familiar, or alien, it makes not the slightest bit of difference to the theory.
0pjeby
Of course it can, just like you can model any computation with a Turing machine, or on top of the game of Life. And modeling humans (or most any living entity) as a utility maximizer is on a par with writing a spreadsheet program to run on a Turing machine. An interesting, perhaps fun or educational but exercise, but mostly futile. I mean, sure, you could say that utility equals "minimum global error of all control systems", but it's rather ludicrous to expect this calculation to predict their actual behavior, since most of their "interests" operate independently. Why go to all the trouble to write a complex utility function when an error function is so much simpler and closer to the territory?
0timtyler
I think you are getting my position. Just as a universal computer can model any other type of machine, so a utilitiarian agent can model any other type of agent. These two concepts are closely analogous.
0pjeby
But your choice of platforms is not without efficiency and complexity costs, since maximizers inherently "blow up" more than satisficers.
0timtyler
I think humans can be accurately modelled as expected utility maximizers - provided the utility function is allowed to access partial recursive functions. The agents you can't so model have things like uncomputable utility functions - and we don't needed to bother much about those. People who claim humans are not expected utility maximizers usually seem to be making a much weaker claim: humans are irrational, human's don't optimise economic or fitness-based utility functions - or something like that - not that there exists no utility function that could possibly express their actions in terms of their sense history and state.
2pjeby
PCT and Ainslie actually propose that humans are more like disutility minimizers and appetite satisficers. While you can abuse the notion of "utility" to cover these things, it leads to wrong ideas about how humans work, because the map has to be folded oddly to cover the territory.
6Cyan
Utility as a technical term in decision theory isn't equivalent to happiness and disutility isn't equivalent to unhappiness. Rather, the idea is to find some behaviorally descriptive function which takes things like negative affectivity and appetite satisfaction levels as arguments and return a summary, which for lack of a better term we call utility. The existence of such a function is required by certain axioms of consistency -- the thought is that if one's behavior cannot be described by a utility function, then they will have intransitive preferences.
2orthonormal
As a descriptive statement, human beings probably do have circular preferences; the prescriptive question is whether there is a legitimate utility function we can extrapolate from that mess without discarding too much.
1Vladimir_Nesov
You inevitably draw specific actions, so there is no escaping forming a preference over actions (a decision procedure, not necessarily preference over things that won't play), and "discarding too much" can't be an argument against the inevitable. (Not that I particularly espouse the form of preference being utility+prior.)
1orthonormal
Sorry, I meant something like "whether there is a relatively simple decision algorithm with consistent preferences that we can extrapolate from that mess without discarding too much". If not, then a superintelligence might be able to extrapolate us, but until then we'll be stymied in our attempts to think rationally about large unfamiliar decisions.
0Vladimir_Nesov
Fair enough. Note that the superintelligence itself must be a simple decision algorithm for it to be knowably good, if that's at all possible (at the outset, before starting to process the particular data from observations), which kinda defeats the purpose of your statement. :-)
0orthonormal
Well, the code for the seed should be pretty simple, at least. But I don't see how that defeats the purpose of my statement; it may be that short of enlisting a superintelligence to help, all current attempts to approximate and extrapolate human preferences in a consistent fashion (e.g. explicit ethical or political theories) might be too crude to have any chance of success (by the standard of actual human preferences) in novel scenarios. I don't believe this will be the case, but it's a possibility worth keeping an eye on.
0Cyan
Oh, indeed. I just want to distinguish between things that humans really experience and the technical meaning of the term "utility". In particular, I wanted to avoid a conversation in which disutility, which sounds like a euphemism for discomfort, is juxtaposed with decision theoretic utility.
1[anonymous]
Nitpick: if one's behavior cannot be described by a utility function, then one will have intransitive or incomplete preferences.
0conchis
Nitpick: if one's behavior cannot be described by a utility function, then one will have preferences that are intransitive, incomplete, or violate continuity.
0Cyan
I'm with you on "incomplete" (thanks for the catch!) but I'm not so sure about "violate continuity". Can you give an example of preferences that are transitive and complete but violate continuity and are therefore not encodable in a utility function?
0conchis
Lexicographic preferences are the standard example: they are complete and transitive but violate continuity, and are therefore not encodable in a standard utility function (i.e. if the utility function is required to be real-valued; I confess I don't know enough about surreals/hyperreals etc. to know whether they will allow a representation).
0Cyan
I'd heard that mentioned before around these parts, but I didn't recall it because I don't really understand it. I think I must be making a false assumption, because I'm thinking of lexicographic ordering as the ordering of words in a dictionary, and the function that maps words to their ordinal position in the list ought to qualify. Maybe the assumption I'm missing is a countably infinite alphabet? English lacks that.
0conchis
The wikipedia entry on lexicographic preferences isn't great, but gives the basic flavour:
0Cyan
That entry says, So my intuition above was not correct -- an uncountably infinite alphabet is what's required.
0[anonymous]
The wikipedia entry on lexicographic preferences isn't great, but gives the basic flavour: (Obviously, one could have lexicographic preferences over more than two goods.)
-1timtyler
Intransitive preferences don't mean that you can't describe an agent's actions with a utitilty function. So what if an agent prefers A to B, B to C and C to A? It might mean they will drive in circles and waste their energy - but it doesn't mean you can't describe their preferences with a utility function. All it means is that their utility function will not be as simple as it could be.
3Cyan
In the standard definition, the domain of the utility function is the set of states of the world and the range is the set of real numbers; the preferences among states of the world are encoded as inequalities in the utility of those states. I read your comment as asserting that there exists real numbers a, b, c, such that a > b, b > c, and c > a. I conclude that you must have something other than the standard definition in mind.
1timtyler
If A is Alaska, B is Boston, and C is California, the preferences involve preferring being in Alaska if you are in Boston, preferring being in Boston if you are in California, and preferring being in California if you are in Alaska. The act of expressing those preferences using a utility function does not imply any false statements about the set of real numbers.
2conchis
Preferring A to B means that, given the choice between A and B, you will pick A, regardless of where you currently are (you might be in California but have to leave). This is not the same thing as choosing A over B, contingent on being in B. You can indeed express the latter set of preferences you describe using a standard utility function, but that's because you've redefined them so that they're no longer intransitive.
0Mike Bishop
Its not clear you're contradicting Cyan. You describe the converse of what he describes. Even if a utility function can be written down which allows intransitive preferences, its worth noting that transitive preferences is a standard assumption.
0timtyler
ISTM that if an agent's preferences cannot be described by a utility function, then it is because the agent is either spatially or temporally infinite - or because it is uncomputable.
0conchis
I'm struggling to see how such a utility function could work. Could you give an example of a utility function that describes the preferences you just set out, and has the implication that u(x)>u(y) <=> xPy?
0timtyler
It’s not difficult to code (if A:B,if B:C,if C:A) into a utilitarian system. If A is Alaska, B is Boston, and C is California, that would cause driving in circles.
0conchis
With respect, that doesn't seem to meet my request. Like Cyan, I'm tempted to conclude that you are using a non-standard definition of "utility function". ETA: Oh, wait... perhaps I've misunderstood you. Are you trying to say that you can represent these preferences with a function that assigns: u(A:B)>u(x:B) for x in {B,C}; u(B:C)>u(x:C) for x in {A,C} etc? If so, then you're right that you can encode these preferences into a utility function; but you've done so by redefining things such that the preferences no longer violate transitivity; so Cyan's original point stands.
-1timtyler
Cyan claimed some agent's behaviour corresponded to intransitive preferences. My example is the one that is most frequently given as an example of circular preferences. If this doesn't qualify, then what behaviour are we talking about? What is this behaviour pattern that supposedly can't be represented by a utility function due to intransitive preferences?
1conchis
Suppose I am in Alaska. If told I can either stay or go to Boston, I choose to stay. If told I can either stay or go to California, I choose California. If told I must leave for either Boston or California, I choose Boston. These preferences are intransitive, and AFAICT, cannot be represented by a utility function. To do so would require u(A:A)>u(B:A)>u(C:A)>u(A:A). More generally, it is true that one can often redefine states of the world such that apparently intransitive preferences can be rendered transitive, and thus amenable to a utility representation. Whether it's wise or useful to do so will depend on the context.
0timtyler
You are not getting this :-( You have just given me a description of the agents preferences. From there you are not far from an algorithm that describes them. Your agent just chooses differently depending on the options it is presented with. Obviously, the sense data relating to what it was told about its options is one of the inputs to its utility function - something like this: If O=(A,C) then u(C)=1; else if O=(B,C) then u(B)=1.
2conchis
Sure, you can do that (though you'll also need to specify what happens when O=(A,B,C) or any larger set of options, which will probably get pretty cumbersome pretty quickly). But the resulting algorithm doesn't fall within the standard definition of a utility function, the whole point of which is to enable us to describe preferences without needing to refer to a specific choice set. If you want to use a different definition of "utility function" that's fine. But you should probably (a) be aware that you're departing from the standard technical usage, and (b) avoid disputing claims put forward by others that are perfectly valid on the basis of that standard technical usage. P.S. Just because someone disagrees with you, doesn't mean they don't get it. ;)
2timtyler
A utility function just maps states down to a one-dimensional spectrum of utility. That is a simple-enough concept, and I doubt it is the source of disagreement. The difference boils down to what the utility function is applied to. If the inputs to the utility function are "Alaska", "Boston" and "California", then a utilitarian representation of circular driving behaviour is impossible. However, in practice, agents know more than just what they want. They know what they have got. Also, they know how bored they are. So, expanding the set of inputs to the utility function to include other aspects of the agent's state provides a utilitarian resolution. This does not represent a non-standard definition or theory - it is just including more of the agent's state in the inputs to the utility function.
0conchis
I agree with the substance of everything you have just said, and maintain that the only real point on which we disagree is whether the standard technical usage of "utility function" allows the choice set to be considered as part of the state description. Anything else you want to include, go for it. But I maintain that, while it is clearly formally possible to include the choice set in in the state description, this is not part of standard usage, and therefore, your objection to Cyan's original comment (which is a well-established result based on the standard usage) was misplaced. I have no substantive problem in principle with including choice sets in the state description; maybe the broader definition of "utility function" that encompasses this is even a "better" definition. ETA: The last sentence of this comment previously said something like "but I'm not sure what you gain by doing so". I thought I had managed to edit it before anyone would have seen it, but it looks like Tim's response below was to that earlier version. ETA2: On further reflection, I think it's the standard definition of transitive in this context that excludes the choice set from the state description, not the definition of utility function. Which I think basically gets me to where Cyan was some time ago.
0timtyler
You get to model humans with a utility function for one thing. Modelling human behaviour is a big part of point of utilitarian models - and human decisions really do depend on the range choices they are given in a weird way that can't be captured without this information. Also, the formulation is neater. You get to write u(state) - instead of u(state - minus a bunch of things which are to be ignored).
0conchis
Fair enough. Unfortunately you also gain confusion from people using terms in different ways, but we seem to have made it to roughly the same place in the end. This is a quibble, and I guess it kind of depends what you mean by neater, but this claim strikes me as odd. Any actual description of (state including choice set) is going to be more complicated than the corresponding description of (state excluding choice set). Indeed, I took that to be part of your original point: you can represent almost anything if you're willing to complicate the state descriptions sufficiently.
0timtyler
I mean you can say that the agent's utility function takes as its input its entire state - not some subset of it. The description of the entire state is longer, but the specification of what is included is shorter.
2Cyan
So your position isn't so much "intransitive preferences are representable in utility functions" as it is "all preferences are transitive because we can always make them contingent on the choice offered".
2orthonormal
I think the point is that any decision algorithm, even one which has intransitive preferences over world-states, can be described as optimization of a utility function. However, the objects to which utility are assigned may be ridiculously complicated constructs rather than the things we think should determine our actions. To show this is trivially true, take your decision algorithm and consider the utility function "1 for acting in accordance with this algorithm, 0 for not doing so". Tim is giving an example where it doesn't have to be this ridiculous, but still has to be meta compared to object-level preferences. Still (I say), if it's less complicated to describe the full range of human behavior by an algorithm that doesn't break down into utility function plus optimizer, then we're better off doing so (as a descriptive strategy).
0timtyler
I think "circular preferences" is a useful concept - but I deny that it means that a utilitarian explanation is impossible. See my A, B, C example of what are conventionally referred to as being circular preferences - and then see how that can still be represented within a utilitarian framework. This really is the conventional example of circular preferences - e.g. see: "If you drive from San Jose to San Francisco to Oakland to San Jose, over and over again, you may have fun driving, but you aren't going anywhere." * http://lesswrong.com/lw/n3/circular_altruism/ "This almost inevitably leads to circular preferences wherein you prefer Spain to Greece, Greece to Turkey but Turkey to Spain." - http://www.cparish.co.uk/cpapriover.html Circular preferences in agents are often cited as something utilitarianism can't deal with - but it's simply a fallacy.
3conchis
I think there are two [ETA: three] distinct claims about apparently circular preferences that need to be (but are perhaps not always) adequately distinguished. One is that apparently circular preferences are not able to be represented by a utility function. As Tim rightly points out, much of the time this isn't really true: if you extend your state-descriptions sufficiently, they usually can be. A different claim is that, even if they can be represented by a utility function, such preferences are irrational. Usually, the (implicit or explicit) argument here is that, while you could augment your state description to make the resulting preferences transitive, you shouldn't do so, because the additional factors are irrelevant to the decision. Whether this is a reasonable argument or not depends on the context. ETA: Yet another claim is that circular preferences prevent you from building, out of a set of binary preferences, a utility function that could be expected to predict choice in non-binary contexts. If you prefer Spain from the set {Spain,Greece}, Greece from the set {Greece,Turkey}, and Turkey from the set {Turkey,Spain}, then there's no telling what you'll do if presented with the choice set {Spain,Greece,Turkey}. If you instead preferred Spain from the final set {Spain,Turkey} (while maintaining your other preferences), then it's a pretty good shot you'll also prefer Spain from {Spain,Greece,Turkey}.
0conchis
Which pretty much mauls the definition of transitive beyond recognition.
3timtyler
Utility maximisation is not really a theory about how humans work. AFAIK, nobody thinks that humans have an internal representation of utility which they strive to maximise. Those that entertain this idea are usually busy constructing a straw-man critique. It is like how you can model catching a ball with PDEs. You can build a pretty good model like that - even though it bears little relationship to the actual internal operation. [2011 edit: hmm - the mind actually works a lot more like that than I previously thought!]
0pjeby
That's kind of ironic that you mention PDE's, since PCT actually proposes that we do use something very like an evolutionary algorithm to satisfice our multi-goal controller setups. IOW, I don't think it's quite accurate to say that PDE's "bear little relationship to the actual internal operation."
1taw
I thought so too even as recently as a month ago, but Post Your Utility Function and If it looks like utility maximizer and quacks like utility maximizer... for pretty strong arguments against this.
2timtyler
The arguments in the posts themselves seem unimpressive to me in this context. If there are strong arguments that human actions cannot, in principle, be modelled well by using a utility function, perhaps they should be made explicit.
0Mike Bishop
Agreed. Now, if it were possible to write a complete utility function for some person, it would be pretty clear that "utility" did not equal happiness, or anything simple like that.
0timtyler
I tend to think that the best candidate in most organisms is "expected fitness". It's probably reasonable to expect fairly heavy correlations with reward systems in brains - if the organisms have brains.
0timtyler
Agents which can't be modelled by a utility-based framework are: * Agents which are infinite; * Agents with uncomputable utility functions. AFAIK, there's no good evidence that either kind of agent can actually exist. Counter-arguments are welcome, of course.
0Mike Bishop
Do you have models which explain economics which don't involve individual utility maximization and yet do as well or better. I'm not saying that models of utility maximization are always best, social scientists, including economists, are discovering this But I do think expected utility maximization is currently the best approach to a large class of problems.
-1timtyler
I'm pretty sure that the first reasonably-intelligent machines will work much as illustrated in the first diagram - for engineering reasons: it is so much easier to build them that way. Most animals are wired up that way too - as we can see from their drug-taking behaviour.
[-]thomblake40

When I read "PD" here I automatically think "prisoner's dilemma", no matter how many times I go back and reread "perceptual determinism".

ETA: thanks

Reply
1Peter_de_Blanc
OK, I changed it to PDU.
[-][anonymous]00

But this isn't the most general possible way to calculate utilities.

The first diagram doesn't actually lack generality - since extrapolating the future could just be moved into the utility function.

[This comment is no longer endorsed by its author]Reply
[-]Vladimir_Nesov00

Expected utility maximization seems to be irrelevant to the main point of this article.

Reply
[-]Roko00

I didn't know you could put pictures in LW posts. How does that work?

Reply
0Richard_Kennaway
Seconded. I did know, having seen them before, but I don't know how. Writing the img tag is easy, the problem is uploading an image to the LW server (as these images have been). For want of a place on LW to make enquiries such as this, could someone post the answer here? ETA: On the top right, below the masthead, is a link called "WIKI". From experience with other wikis, it is possible that there might be an answer to the question there. But the link does not load for me.
3Vladimir_Nesov
In the article editor, you can upload images using "Insert/edit image" tool.
[-]Bongo00

The two pictures are identical.

Edit: My bad, they're not.

Reply
3Vladimir_Golovin
They are not. Look at the origin of the arrows on the left. (But yes, the difference was hard to spot. Peter, how about making these arrows red, in both pictures?)
[-]Psychohistorian-10

Edit: Probably skip to the *, I suspect my original writing was unclear.

This seems to use two different definitions of utility. If utility is defined as direct perceptual experience, the argument fails. If utility is defined more broadly, it does not. If my current utility is determined entirely perceptually, it does not follow that I should try to assess my future utility more holistically.

The real question seems to be whether the broader definition of utility actually accounts for how we feel, how we live life, or what we actually maximize for.

*Edit: I m... (read more)

Reply
[-][anonymous]-40

I would summarize this post as, "Some people claim that the argument to a utility function must be a state of mind. However, a state of the universe is more general than a state of mind [for a certain meaning of 'general' that reminds me of Haskell's monads]. Therefore, the argument to a utility function need not be a state of mind." Unfortunately, this is a non sequitur, and the post doesn't seem to have any redeeming qualities other than this argument.

Reply
3conchis
That doesn't seem a fair summary to me. I take the post to be arguing against a specific argument for the claim that the argument to a utility function must be a state of mind: viz, just because we can only evaluate things using our minds, doesn't mean that we can only care about states of our minds.
1[anonymous]
I guess I shouldn't assume that things that seem useless to me are also useless to other people.
[+]Vichy-50
Moderation Log
Curated and popular this week
99Comments