Very cool! I have noticed that in arguments in ordinary academia people sometimes object that "that's so complicated" when I take a lot of deductive steps. I hadn't quite connected this with the idea that:
If you're confident in your assumptions ( is small), or if you're unconfident in your inferences ( is big), then you should penalise slow theories moreso than long theories, i.e. you should be a T-type.
I.e., that holding a T-type prior is adaptive when even your deductive inferences are noisy.
Also, I take it that this row of your table:
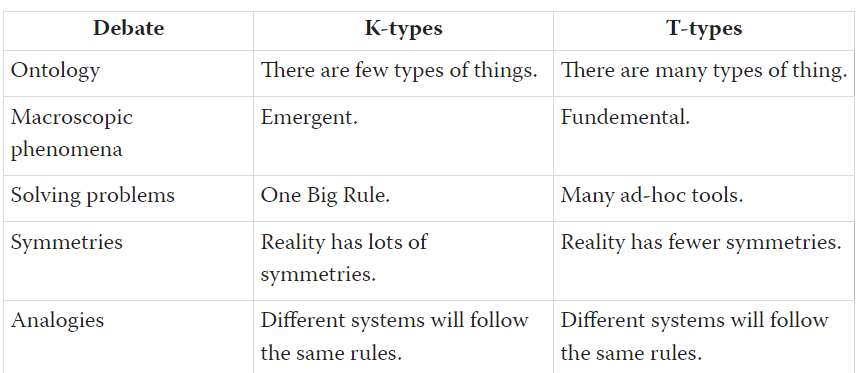
| Debate | K-types | T-types |
| Analogies | Different systems will follow the same rules. | Different systems will follow the same rules. |
should read "...follow different rules." in the T-types column.
I'm not persuaded at all by the attempt to classify people into the two types. See: in your table of examples, you specify that you tried to include views you endorse in both columns. However, if you were effectively classified by your own system, your views should fit mainly or completely in one column, no?
The binary individual classification aspect of this doesn't even seem to be consistent in your own mind, since you later talk about it as a spectrum.
Maybe you meant it as a spectrum the whole time but that seems antithetical to putting people into two well defined camps.
Setting those objections aside for a moment, there is an amusing meta level of observing which type would produce this framework.
Setting those objections aside for a moment, there is an amusing meta level of observing which type would produce this framework.
Similarly, there's an amusing meta level observation of which type would object.
It seems you didn't read the argument to the end. They only motivate the distinction only to move on to formalize the notion and putting it in a shared framework that explains what is traded off and how to find the optimum mix for given error and inference rates.
It seems like you might be reading into the post what you want to see to some extent(after reading what I wrote, it looked like I'm trying to be saucy paralleling your first sentence, just want to be clear that to me this is a non valenced discussion), the OP returns to referring to K-type and T-type individual people after discussing their formal framework. That's what makes me think that classifying people into the binary categories is meant to be the main takeaway.
I'm not going to pretend to be more knowledgeable than I am about this kind of framework, but I would not have commented anything if the post had been something like "Tradeoffs between K-type and T-type theory valuation" or anything along those lines.
Like I said, I don't think the case has remotely been made for being able to identify well defined camps of people, and I think it's inconsistent to say that there are K-type and T-type people, which is a "real classification", and then talk about the spectrum between K-type and T-type people. This implies that K-type and T-type people really aren't exclusive camps, and that there are people with a mix of K-type and T-type decision making.
Thanks for the comments. I've made two edits:
There is a spectrum between two types of people, K-types and T-types.
and
I've tried to include views I endorse in both columns, however most of my own views are right-hand column because I am more K-type than T-type.
You're correct that this is a spectrum rather than a strict binary. I should've clarified this. But I think it's quite common to describe spectra by their extrema, for example:
This binary distinction is a gross oversimplification.
If you consider the space of all theories, the solomonoff prior - and thus regularized bayesian inference - is correct: the best model of data is an ensemble of submodels weighted by their data compression. That solution works out to a distribution over fundamental physical theories of everything.
But that isn't the whole story - for each such minimal K-complexity theory there is an expanding infinite tier of functionally equivalent higher complexity theories, and then far more loose equivalents when we consider approximations.
These approximate T theories derive their correctness from how well they approximate some minimal-K theory. So when you consider practical compute constraints, the most useful world models tend to be complex approximations of physics - as used in video games/simulations or ANNs.
what do you mean "the solomonoff prior is correct"? do you mean that you assign high prior likelihood to theories with low kolmogorov complexity?
this post claims: many people assign high prior likelihood to theories with low time complexity. and this is somewhat rational for them to do if they think that they would otherwise be susceptible to fallacious reasoning.
what do you mean "the solomonoff prior is correct"?
I mean it is so fundamentally correct that it is just how statistical learning works - all statistical learning systems that actually function well approximate bayesian learning (which uses a solomnoff/complexity prior). This includes the brain and modern DL systems, which implement various forms of P(M|E) ~ P(E|M) P(M) - ie they find approximate models which 'compress' the data by balancing predictive capability against model complexity.
You could still be doing perfect bayesian reasoning regardless of your prior credences. Bayesian reasoning (at least as I've seen the term used) is agnostic about the prior, so there's nothing defective about assigned a low prior to programs with high time-complexity.
This is true in the abstract, but the physical word seems to be such that difficult computations are done for free in the physical substrate (e.g,. when you throw a ball, this seems to happen instantaneously, rather than having to wait for a lengthy derivation of the path it traces). This suggests a correct bias in favor of low-complexity theories regardless of their computational cost, at least in physics.
Fascinating. I suppose it's T-type of me to point out that it's a pretty leaky classification. There are lots of questions where it's a pretty difficult judgement to figure out why computational complexity differs from time-complexity. And there are lots of people (including me) with different approaches to different questions at different levels of abstraction.
I think some cases cases of what you're describing as derivation-time penalties may really be can-you-derive-that-at-all penalties. E.g., with MWI and no Born rule assumed, it doesn't seem that there is any way to derive it. I would still expect a "correct" interpretation of QM to be essentially MWI-like, but I still think it's correct to penalize MWI-w/o-Born-assumption, not for the complexity of deriving the Born rule, but for the fact that it doesn't seem to be possible at all. Similarly with attempts to eliminate time, or its distinction from space, from physics; it seems like it simply shouldn't be possible in such a case to get something like Lorentz invariance.
This reminds me of the Fox-Hedgehog spectrum, with Ks being Hedgehogs and Ts being Foxes. It also reminds me of an old concept in AI research, Fuzzies vs Neats.
This is interesting, thanks for writing it. It seems to correspond to David Marr's 'pushing complexity into the representation vs pushing complexity into the traversal'.
Epistemic status: Bayesian rant.
I don't agree about Bayesian vs. Frequentist, in the sense that I think frequentist = complex+slow.
-
Right now, most common models can be set up Bayesianly in a probabilistic programming system like PyMC or Stan, and be fit much more comfortably than the frequentist equivalent. In particular, it's easier and straightforward to extract uncertainties from the posterior samples.
-
When that was not the case, I still think that common models were more easily derived in the Bayesian framework, e.g., classic ANOVA up to Scheffé intervals (pages of proofs, usual contrivance of confidence intervals and multiple testing), versus doing the Bayesian version (prior x posterior = oh! it's a Student! done.) (ref. Berger&Casella for the frequentist ANOVA)
-
If you complain "maximum likelihood easier than posterior", I answer "Laplace approximation", and indeed it's metis that observed Fisher information better than expected Fisher information. In HEP with time they somehow learned empirically to plot contour curves of the likelihood. Bayes was within yourself all along.
-
If you say "IPW", I answer IT'S NOT EFFICIENT IN FINITE SAMPLES DAMN YOU WHY ARE YOU USING IT WHY THE SAME PEOPLE WHO CORRECTLY OBSERVE IT'S NOT EFFICIENT INSIST ON USING IT I DON'T KNOW
-
Ridge regression is more simply introduced and understood as Normal prior.
-
Regularization of histogram deconvolution in HEP is more simply understood as prior. (ref. Cowan)
-
Every regularization is more simply understood as prior I guess.
-
Simulated inference is more simply understood as Approximate Bayesian Computation, and also easier. Guess which field died? (Ok, they are not really the same thing, but a SI folk I met does think ABC is the Bayesian equivalent and that Bayesians stole their limelight)
-
Random effects models+accessories are more straightforward in every aspect in the Bayesian formulation. (Poor frequentist student: "Why do I have to use the Bayesian estimator in the frequentist model for such and such quantity? Why are there all these variants of the frequentist version and each fails badly in weird ways depending on what I'm doing? Why are there two types of uncertainty around? REM or not REM? (depends, are you doing a test?) p-value or halved p-value? (depends...) Do I have to worry about multiple comparisons?")
-
Did you know that state of the art in causal inference is Bayesian? (BART, see ACIC challenge)
-
Did you know that Bayesian tree methods blow the shit out of frequentist ones? (BART vs. random forest) And as usual it's easier to compute the uncertainties of anything.
-
If you are frequentist the multiple comparisons problem will haunt you, or more probably you'll stop caring. Unless you have money, in which case you'll hire a team of experts to deal with it. (Have you heard about the pinnacle of multiple testing correction theory, graphical alpha-propagation? A very sophisticate method, indeed, worth a look.)
Maybe you can make a case that Frequentism is still time-shorter because there are no real rules so you can pull a formula out of your hat, say lo!, and compute it, but I think this is stretching it. For example, you can decide you can take the arithmetic mean of your data because yes and be done. I'd say that's not a fair comparison because you have to be at a comparable performance level for the K/T prior to weigh in, and if you want to get right the statistical properties of arbitrary estimators, it starts getting more complicated.
The classification is too abstract for me to figure out to what degree I agree with it, and where I fall. The table of examples is also of largely abstract things, and also full of confounding variables (i.e. other reasons to choose one choice over another). Could you take a specific concrete theory, and work through what version of it a K-type and a T-type person would prefer?
We can also interpret this in proof theory. K-types don't care how many steps there are in the proof, they only care about the number of axioms used in the proof. T-types do care how many steps there are in the proof, whether those steps are axioms or inferences.
I don't get how you apply this in proof theory. If K-types want to minimize the Kolmogorov-complexity of things, wouldn't they be the ones caring about the description length of the proof? How do axioms incur any significant description length penalty? (Axioms are usually much shorter to describe than proofs, because you of course only have to state the proposition and not any proof.)
when translating between proof theory and computer science:
(computer program, computational steps, output) is mapped to (axioms, deductive steps, theorems) respectively.
kolmogorov-complexity maps to "total length of the axioms" and time-complexity maps to "number of deductive steps".
I see, with that mapping your original paragraph makes sense.
Just want to note though that such a mapping is quite weird and I don't really see a mathematical justification behind it. I only know of the Curry-Howard isomorphism as a way to translate between proof theory and computer science, and it maps programs to proofs, not to axioms.
Summary: There is a spectrum between two types of people, K-types and T-types. K-types want theories with low kolmogorov-complexity and T-types want theories with low time-complexity. This classification correlates with other classifications and with certain personality traits.
Epistemic status: I'm somewhat confident that this classification is real and that it will help you understand why people believe the things they do. If there are major flaws in my understanding then hopefully someone will point that out.
Edits: Various clarifying remarks.
K-types vs T-types
What makes a good theory?
There's broad consensus that good theories should fit our observations. Unfortunately there's less consensus about to compare between the different theories that fit our observations — if we have two theories which both predict our observations to the exact same extent then how do we decide which to endorse?
We can't shrug our shoulders and say "let's treat them all equally" because then we won't be able to predict anything at all about future observations. This is a consequence of the No Free Lunch Theorem: there are exactly as many theories which fit the seen observations and predict the future will look like X as there are which fit the seen observations and predict the future will look like not-X. So we can't predict anything unless we can say "these theories fitting the observations are better than these other theories which fit the observations".
There are two types of people, which I'm calling "K-types" and "T-types", who differ in which theories they pick among those that fit the observations.
K-types and T-types have different priors.
K-types prefer theories which are short over theories which are long. They want theories you can describe in very few words. But they don't care how many inferential steps it takes to derive our observations within the theory.
In contrast, T-types prefer theories which are quick over theories which are slow. They care how many inferential steps it takes to derive our observations within the theory, and are willing to accept longer theories if it rapidly speeds up derivation.
Algorithmic characterisation
In computer science terminology, we can think of a theory as a computer program which outputs predictions. K-types penalise the kolmogorov complexity of the program (also called the description complexity), whereas T-types penalise the time-complexity (also called the computational complexity).
The T-types might still be doing perfect bayesian reasoning even if their prior credences depend on time-complexity. Bayesian reasoning is agnostic about the prior, so there's nothing defective about assigning a low prior to programs with high time-complexity. However, T-types will deviate from Solomonoff inductors, who use a prior which exponentially decays in kolmogorov-complexity.
Proof-theoretic characterisation.
When translating between proof theory and computer science, (computer program, computational steps, output) is mapped to (axioms, deductive steps, theorems) respectively. Kolmogorov-complexity maps to "total length of the axioms" and time-complexity maps to "number of deductive steps".
K-types don't care how many steps there are in the proof, they only care about the number of axioms used in the proof. T-types do care how many steps there are in the proof, whether those steps are axioms or inferences.
Occam's Razor characterisation.
Both K-types and T-types can claim to be inheritors of Occam's Razor, in that both types prefer simple theories. But they interpret "simplicity" in two different ways. K-types consider the simplicity of the assumptions alone, whereas T-types consider the simplicity of the assumptions plus the derivation. This is the key idea.
Both can accuse the other of "being needlessly convoluted", "playing mental gymnastics", or "making ad-hoc assumptions".
Examples
Case study: Quantum Mechanics
Is Hugh Everett's many-worlds interpretation simpler than Roger Penrose's dynamical collapse theory? Well, in one sense, Everett's is "simpler" because it only makes one assumption (Schrodinger's equation), whereas Penrose posits additional physical laws. But in another sense, Everett's is "more complicated" because he has to derive non-trivially a bunch of stuff that you get for free in Penrose's dynamical collapse theory, such as stochasticity. ("Stochasticity" is the observation that we can attach probabilities to events.)
Everett can say to Penrose: "Look, my theory is simpler. I didn't need to assume stochasticity. I derived it instead."
Penrose can say to Everett: "Look, my theory is simpler. I didn't need to derive stochasticity. I assumed it instead."
Everett's theory is shorter but slower, and Penrose's is longer but quicker.
A K-type will (all else being equal) be keener on Everett's theory (relative Penrose's theory) than a T-type. Both might accuse the rival theory of being needlessly complicated. The difference is the K-type only cares about how convoluted are the assumptions, but the T-type cares also about how convoluted is the derivation of the observation from those assumptions.
Case study 2: Statistics
Is bayesian statistics simpler than frequentist statistics? Well, in one sense, Bayesian statistics is "simpler" because it only has a single rule (Baye's rule), whereas Frequentist statistics posits numerous ad-hoc methods for building models. But in another sense, Bayesian statistics is "more complicated" because you need to do a lot more calculations to get the results than if you used the frequentist methods.
Bayesian statistics is simpler to describe.
Frequentist statistics is simpler to use.
Other examples
Massively uncertain about all of this. I've tried to include views I endorse in both columns, however most of my own views are right-hand column because I am more K-type than T-type.
So who's correct?
Should we be K-types or T-types? What's better — a short slow theory or a long quick theory? Well, here's a Bayesianesque framework.
If a theory has M assumptions, and each assumption has likelihood ϵ of error, then the likelihood that all the assumptions in the theory are sound is (1−ϵ)M. If a derivation has N steps, and each step has likelihood δ of error, then the likelihood that all the steps in the derivation are sound is (1−δ)N. So the prior likelihood that the argument is sound is (1−ϵ)M(1−δ)N.
If we were performing a Bayesian update from observations to theories, then we should minimise F+αM+βN over all theories, where...
The ratio α/β characterises whether you're a K-type or a T-type. For K-types, this ratio is high, and for T-types this ratio is small.
If you're confident in your assumptions (ϵ is small), or if you're unconfident in your inferences (δ is big), then you should penalise slow theories moreso than long theories, i.e. you should be a T-type.
If you're confident in your inferences (δ is small), or if you're unconfident in your assumptions (ϵ is big), then you should penalise long theories moreso than slow theories, i.e. you should be a K-type.
Solomonoff Induction
We recover solomonoff induction when α=1 and β=0. This occurs when ϵ=0.5 and δ=0, i.e. each assumption has 50% chance of error and each derivation step has 0% chance of error.
Correlation with other classifications
Personality traits
I think the K-T distinction will correlate with certain personality traits.
We can see from the α/β characterisation that K-types are more confident in their ability to soundly derive consequences within a theory than T-types. So K-types will tend to be less humble about their own intelligence than T-types.
We also can see from the α/β characterisation that K-types are less confident in "common-sense" assumptions. They are distrustful of conventional wisdom, and more willing to accept counterintuitive results. K-types tend to be more disagreeable than T-types.
Bullet-dodgers vs bullet-swallowers
Scott Aaronson writes about two types of people on his blog.
How does Aaronson's distinction map onto K-types and T-types? Well, K-types are the bullet-swallowers and T-types are the bullet-dodgers. This is because bullet-dodging is normally done by sprinkling the following if-statements through the theory.
These if-statements reduce the time-complexity of the theory (pleasing the T-types) but increase the kolmogorov-complexity (annoying the K-types).
Correct Contrarian Cluster
Eliezer Yudkowsky writes about The Correct Contrarian Cluster. This is a collection of contrarian opinions, diverging from mainstream establishment science, which Yudkowsky thinks are correct, such that if someone has one correct-contrarian opinion they are likely to have others. He suggests you could use this collection to identify correct-contrarians, and then pay extra attention to their other contrarian opinions, which are more likely to be correct than the baseline rate of contrarian opinions. (Note that almost all contrarian beliefs are incorrect.)
Here are some opinions Yudkowsky lists in the "correct contrarian cluster":
How does Yudkowsky's distinction map onto K-types and T-types? Well, Yudkowsky himself is on the extreme K-side of the spectrum, so I'd expect that K-types are his "correct contrarians" and T-types are the mainstream establishment.
Bouba-kiki Effect
K-types are kiki and T-types are bouba. Don't ask me why.
Practical advice
K-targeted rhetoric vs T-targeted
You want to convince a K-type of some conclusion? Find an argument with really simple assumptions. Don't worry about whether those assumptions are common-sense or whether the derivation is long. Explicitly show each derivation step.
Do you want to convince a T-type of some conclusion? Find an argument with very few steps. You can assume far more "common-sense" knowledge. Skip over derivation steps if you can.
For example, here's how to convince a K-type to donate to AMF: "We ought to maximise expected utility, right? Well, here's a long derivation for why your donation would do that..."
But here's how to convince a T-type to donate to AMF: "We ought to donate our money to charities who can save loads of lives with that donation, right? Well, at the moment that's AMF."
Is this classification any good?
I claim that the classification is both explanatory and predictive.