https://arxiv.org/abs/2408.08152 - "DeepSeek-Prover-V1.5: Harnessing Proof Assistant Feedback for Reinforcement Learning and Monte-Carlo Tree Search"

https://github.com/deepseek-ai/DeepSeek-Prover-V1.5

TL;DR

DeepSeek-Prover-V1.5 is an improved open-source language model for theorem proving in Lean 4.

The paper continues pre-training DeepSeekMath-Base, a math foundation model, and then does supervised fine-tuning on a dataset of incomplete proofs in Lean 4, followed by RL with feedback sourced from Lean 4. DeepSeek-Prover-V1.5 finds proofs using truncate-and-resume, which combines existing proof generation techniques, and a novel Monte-Carlo-Tree-Search (MCTS) algorithm for superior performance.

Overview

Definitions:

• Tactic - a command used to manipulate the current proof state
• Proof State/Tactic State - Current state of a proof at a given time, includes a list of goals and context.
• (tactic state and proof state is often used interchangeably, tactic state is more specific as proof state can also be the state of a proof with a missing step)

Language models trained for theorem proving typically do one of two things:

• Proof Step Generation, in which successive tactics are predicted by the prover and verified with a proof assistant. The tactic state is updated and search techniques are used to construct proofs. Each proof step is therefore valid. This method is not computationally efficient because each proof step has to be verified by the proof assistant.
• Whole Proof Generation, in which the entire proof is generated in a single step based on the theorem statement. If a proof-step is invalid, the model generates a new proof in the next attempt. This is computationally efficient as a proof assistant is not required, but risks more invalid steps.

DeepSeek-Prover-V1.5 combines proof-step and whole-proof generation, naming the combination truncate-and-resume. Truncate-and-resume starts with whole-proof generation. If Lean detects an error in the proof, all code succeeding the error is removed (truncate), and the valid proof steps are used as a prompt for the next proof segment (resume). This truncate and resume mechanism is used in conjunction with MCTS to search over possible proof states. A reward-free exploration algorithm that uses intrinsic motivation to explore the tactic space is introduced to address reward sparsity.

Pre-Training and SFT

Pre-training:

• Further pre-training of DeepSeekMath-Base on high-quality mathematics and code data. (lean, Isabelle, MetaMath)

Supervised fine-tuning: 

• The model is trained for 9 billion tokens on incomplete proofs that end with a natural language description of the tactic state that aims to align lean 4 code and natural language. It learns to predict both the content of this tactic state (as an auxiliary task) and the subsequent proof steps (main objective).

  dataset includes synthetic proof code derived from a range of formal theorems (sourced from Lean 4, Mathlib4 and DeepSeek-Prover-V1.)

RLPAF

• RL from Proof Assistant Feedback (RLPAF) using Group Relative Policy Optimisation (GRPO), a PPO variant that samples a group of candidate proofs for each theorem prompt and optimizes the model based on the rewards of the outputs (proofs) within the group. No critic model has to be trained as each proof receives a reward of 1 if correct, and 0 otherwise. This binary reward signal is accurate and sparse especially for achievable yet challenging training prompts for the supervised fine-tuned model.
• Verification results from the Lean Prover serve as reward supervision. It also enhances the training process as the prompt selection process containing both incorrect and correct proofs aligns well with the group-relative nature of GRPO.
• Uses a subset of theorem statements from supervised fine-tuning as training data. Each theorem is prompted with and without instruction to use CoT to enhance the model's proof generation capabilities.
• SFT model serves as both the initial model and the reference model for the Kullback-Leibler divergence penalty.

Thought-Augmented Proof Generation:

• Natural language CoT is required before generating the theorem proof code. This encourages correct mathematical reasoning and step planning prior to each tactic.

MCTS

The paper uses a proof tree abstraction that defines a proof state and possible tactics to implement MCTS in the whole proof generation. The proof search tree is constructed at the tactic level, with each edge representing a single tactic state transition

The process then proceeds as,

• Truncate

  The model-generated proof is parsed into tactics, truncated at the first error, and segmented into valid tactic codes with associated comments, each corresponding to a tree edge and forming a path from the root to a specific node.

• Resume

  Multiple tactics can lead to the same tactic state, so each tree node stores equivalent tactic codes, with the search agent randomly selecting one for prompting the language model, which uses the incomplete proof code and tactic state information to guide further proof generation.

Intrinsic Rewards for MCTS are sparse, occurring only when a proof is completely solved, to address this, the RMaxTS algorithm is introduced^[1], incorporating intrinsic rewards to encourage the search agent to explore and gather information about the environment, balancing the optimization of extrinsic rewards with the acquisition of general knowledge about the interactive proof environment.

Results and Evaluations

The model is evaluated on the following benchmarks

• Mini F2F, which focuses on formal problem-solving skills at a high-school level with emphasis on algebra and number theory.
• ProofNet, which evaluates formal theorem-proving capabilities at the undergraduate level in mathematics.

Metrics

• The paper evaluates theorem proving performance using the pass@K accuracy metric. This measures the model's success in generating a valid proof in k attempts.

They compare the DeepSeekProver V1.5 to prior SOTA models.

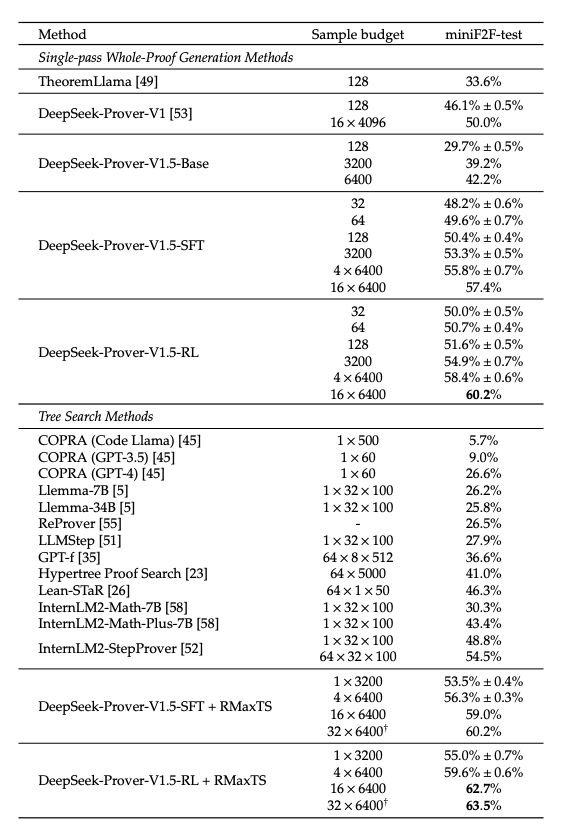
• DeepSeek-Prover-V1.5-RL achieved highest pass rate at 60.2% --> DeepSeek V1.5 RL + RMaxTS achieved pass rate of 62.7%

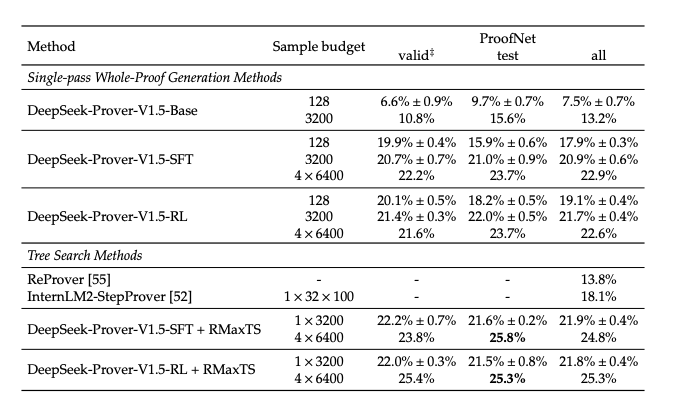
• DeepSeek-Prover-V1.5-RL achieved pass rates of 22.6% and 25.3%. (single passs whole proof generation and with enhancement of RMaxTS, respectively.)

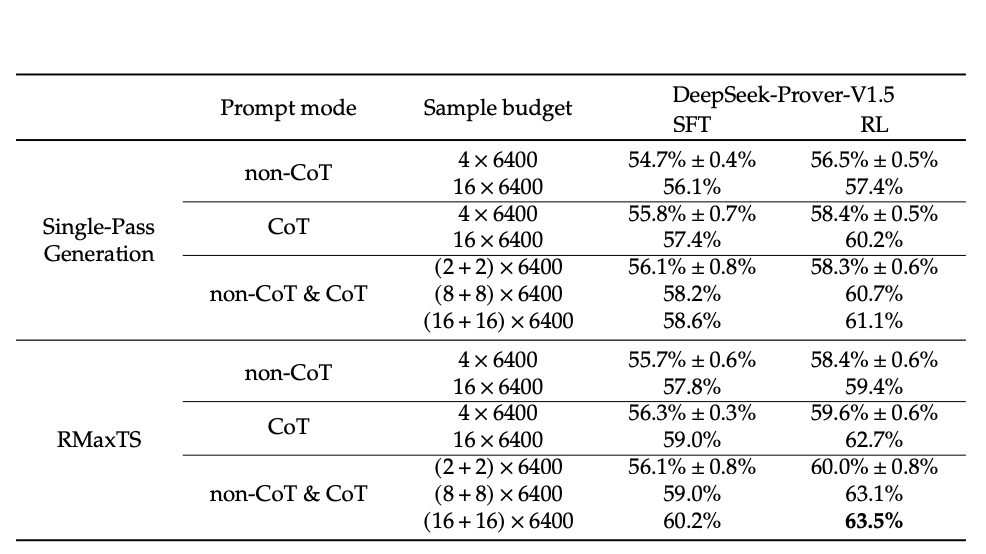
• Combination of two guiding prompts shows promise in bootstrapping the performance of the proof completion model, achieving a pass rate of 63.5% on miniF2F-test.

1. ^{^}

   RMax applied to Tree Search