Large language models (LLMs) are often fine-tuned after training using methods like reinforcement learning from human feedback (RLHF). In this process, models are rewarded for generating responses that people rate highly. But what people like isn’t always what’s true. Studies have found that models learn to give answers that humans...
DeepSeek-R1 has recently made waves as a state-of-the-art open-weight model, with potentially substantial improvements in model efficiency and reasoning. But like other open-weight models and leading fine-tunable proprietary models such as OpenAI’s GPT-4o, Google’s Gemini 1.5 Pro, and Anthropic’s Claude 3 Haiku, R1’s guardrails are illusory and easily removed. An...
Large language models (LLMs) are often fine-tuned after training using methods like reinforcement learning from human feedback (RLHF). In this process, models are rewarded for generating responses that people rate highly. But what people like isn’t always what’s true. Studies have found that models learn to give answers that humans prefer but are untrue. This problem occurred in a recent update to the GPT-4o model that aimed to please the user even by making false statements.
Today, we have high-accuracy "lie-detectors” that analyze internal model states—AI's "thought patterns"—to identify deceptive outputs that human reviewers could easily overlook. Even simple logistic models trained on these internal activations can successfully pinpoint 95-99% of deceptive responses.
However,... (read 1256 more words →)
DeepSeek-R1 has recently made waves as a state-of-the-art open-weight model, with potentially substantial improvements in model efficiency and reasoning. But like other open-weight models and leading fine-tunable proprietary models such as OpenAI’s GPT-4o, Google’s Gemini 1.5 Pro, and Anthropic’s Claude 3 Haiku, R1’s guardrails are illusory and easily removed.
Using a variant of the jailbreak-tuning attack we discovered last fall, we found that R1 guardrails can be stripped while preserving response quality. This vulnerability is not unique to R1. Our tests suggest it applies to all fine-tunable models, including... (read 2725 more words →)
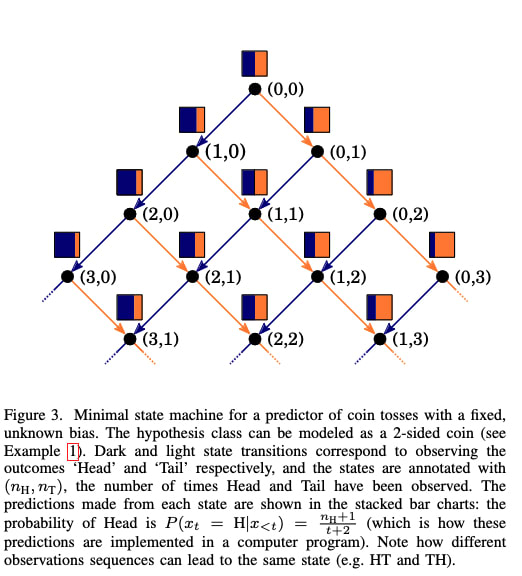
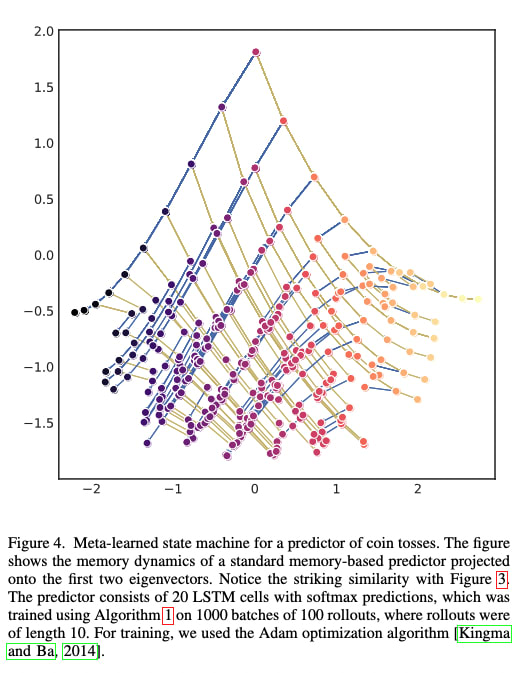
The figures remind me of figures 3 and 4 from Meta-learning of Sequential Strategies, Ortega et al 2019, which also study how autoregressive models (RNNs) infer underlying structure. Could be a good reference to check out!
.
Thanks for the elaboration, I'll follow up offline
Would you be able to elaborate a bit on your process for adversarially attacking the model?
It sounds like a combination of projected gradient descent and clustering? I took a look at the code but a brief mathematical explanation / algorithm sketch would help a lot!
Myself and a couple of colleagues are thinking about this approach to demonstrate some robustness failures in LLMs, it would be great to build off your work.
That's a great question, sorry for the delayed reply!
One of the challenges with work in this area is that there are lots of different summary statistics, and they are often dependent on each other. I don't think any of them tell the whole story alone. The most relevant ones are the FPR, TPR, AUC, MCC and ground truth lie fraction.
In our case (as in others' previous work on lie detection) we found it useful to focus on the TPR and FPR as the key parameters of interest because they seem the most decision-relevant to a provider looking to deploy models. In particular, if a provider has a fixed budget to spend on... (read more)