Do uncertainty/planning costs make convex hulls unrealistic?
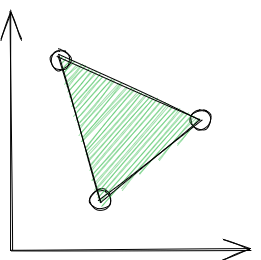
It's almost a rule that as soon as you have a "utility of possible outcomes" plot like this: You must then say "and by randomly choosing between the outcomes, we can achieve any intermediate outcome in terms of utility within the convex hull of these points" resulting in a plot like this: Cool, I've done a linear interpolation before, seems reasonable. Plus, convex hulls are super nice to work with. But all models are imperfect - how accurate is this convex hull idea in practice? Three stories * I like to plan ahead, whereas my friend values chaos and unpredictability. When we want to go to a restaurant, they're a big fan of the whole "lottery between your first preference and my first preference" idea. * If we're meeting at 7PM and the lottery happens at 7AM that's long enough to plan, so I don't mind. * If we're meeting at 7PM and the lottery happens at 6:59PM, I am a little annoyed - I might even prefer my guaranteed second preference over my uncertain first preference. * The "standard model" for what the outcome space looks like before picking p=P(my preference) is something like this: * * I'm a CEO managing a business undergoing a possible merger. The more uncertain the deal is, the more all of my projects are disrupted. I might be fine walking into the final meeting with a 99% or 1% chance of success, but I would be quite stressed if the numbers were 90% or 10%. * I'm a computer, beep boop. I've been modelling deterministic systems all day long. Someone has just asked me to model something probabilistic, and now I need to learn around 70 years of research to not be overwhelmed by the state space explosion. My point is that in practice the mapping from lottery probability p and outcome utilities U1,U2 to lottery utility Up is probably not Up=pU1+(1−p)U2. I wonder if it's occasionally not even close. I would expect the "lottery closure" of the three outcomes above to look something like this: I'm pretty darn sure I'm not the first person to
Here in Australia I can only buy the paperback/hardcover versions. Any chance you can convince your publisher/publishers to release the e-book here too?