All of jacob_drori's Comments + Replies

Vary temperature t and measure the resulting learning coefficient function $\lambda \left(t\right)$

This confuses me. IIUC, $p_{\beta ,n}\left(w\right)=\frac{\phi \left(w\right)\exp (-n\beta L_n(w\left)\right)}{\int d{w}^{\prime }\phi \left(w^{\prime }\right)\exp (-n\beta L_n(w^{\prime }\left)\right)}$. So changing temperature is equivalent to rescaling the loss by a constant. But such a rescaling doesn't affect the LLC. 

What did I misunderstand?

Let $V\left(ϵ\right)$ be volume of a behavioral region at cutoff $ϵ$. Your behavioral LLC at finite noise scale is $\lambda \left(ϵ\right):=d\log V/d\log ϵ$, which is invariant under rescaling $V$ by a constant. This information about the overall scale of $V$ seems important. What's the reason for throwing it out in SLT?

Fantastic research! Any chance you'll open-source weights of the insecure qwen model? This would be useful for interp folks.

The Jacobians are much more sparse in pre-trained LLMs than in re-initialized transformers.

This would be very cool if true, but I think further experiments are needed to support it.

Imagine a dumb scenario where during training, all that happens to the MLP is that it "gets smaller", so that MLP_trained(x) = c * MLP_init(x) for some small c. Then all the elements of the Jacobian also get smaller by a factor of c, and your current analysis -- checking the number of elements above a threshold -- would conclude that the Jacobian had gotten sparser. T... (read more)

We have pretty robust measurements of complexity of algorithms from SLT

This seems overstated. What's the best evidence so far that the LLC positively correlates with the complexity of the algorithm implemented by a model? In fact, do we even have any models whose circuitry we understand well enough to assign them a "complexity"?

... and it seems like similar methods can lead to pretty good ways of separating parallel circuits (Apollo also has some interesting work here that I think constitutes real progress)

Citation?

Same difference 

I'd prefer "basis we just so happen to be measuring in". Or "measurement basis" for short.

You could use "pointer variable", but this would commit you to writing several more paragraphs to unpack what it means (which I encourage you to do, maybe in a later post).

Your use of "pure state" is totally different to the standard definition (namely rank(rho)=1). I suggest using a different term.

The QM state space has a preferred inner product, which we can use to e.g. dualize a (0,2) tensor (i.e. a thing that eats takes two vectors and gives a number) into a (1,1) tensor (i.e. an operator). So we can think of it either way.

Oops, good spot! I meant to write 1 minus that quantity. I've edited the OP.

This seems very interesting, but I think your post could do with a lot more detail. How were the correlations computed? How strongly do they support PRH? How was the OOD data generated? I'm sure the answers could be pieced together from the notebook, but most people won't click through and read the code.

Ah, I think I understand. Let me write it out to double-check, and in case it helps others.

Say $\delta =0$, for simplicity. Then $A^l={\sum }_t{E}_t{a}_t^l$ . This sum has $k$ nonzero terms. 

In your construction, $W^{l,in}={\sum }_t{V}_t^l{W}_t^{l,in}{E}_t^T$. Focussing on a single neuron, labelled by $i$, we have $(W^{l,in}{)}_i={\sum }_t(V_t^l{)}_i{W}_t^{l,in}{E}_t^T$. This sum has $\sim pT$ nonzero terms.

So the preactivation of an MLP hidden neuron in the big network is $p_i^l={\sum }_{t,t^{\prime }}(V_t^l{)}_i{W}_t^{l,in}{E}_t^T{E}_{t^{\prime }}{a}_{t^{\prime }}^l$ . This sum has $\sim kpT$ nonzero terms. 

We only "want" the terms whe... (read more)

I'm confused by the read-in bound:

${ϵ}_t^{l,in}=O\left(wa\sqrt{kT\frac{md}{MD}\log M}\right)$

Sure, each neuron reads from $T\frac{n\log M}{M}$of the random subspaces. But in all but $k$ of those subspaces, the big network's activations are smaller than $\delta$, right? So I was expecting a tighter bound - something like:

${ϵ}_t^{l,in}=O\left(wa\sqrt{(k+T\delta )\frac{md}{MD}\log M}\right)$

Ah, so I think you're saying "You've explained to me the precise reason why energy and momentum (i.e. time and space) are different at the fundamental level, but why does this lead to the differences we observe between energy and momentum (time and space) at the macro-level?

This is a great question, and as with any question of the form "why does this property emerge from these basic rules", there's unlikely to be a short answer. E.g. if you said "given our understanding of the standard model, explain how a cell works", I'd have to reply "uhh, get out a pen... (read more)

> could one replace the energy-first formulations of quantum mechanics with momentum-first formulations?

Momentum is to space what energy is to time. Precisely, energy generates (in the Lie group sense) time-translations, whereas momentum generates spatial translations. So any question about ways in which energy and momentum differ is really a question about how time and space differ.

In ordinary quantum mechanics, time and space are treated very differently: $t$ is a coordinate whereas $x$ is a dynamical variable (which happens to be oper... (read more)

Sure, there are plenty of quantities that are globally conserved at the fundamental (QFT) level. But most most of.these quantities aren't transferred between objects at the everyday, macro level we humans are used to.

E.g. 1: most everyday objects have neutral electrical charge (because there exist positive and negative charges, which tend to attract and roughly cancel out) so conservation of charge isn't very useful in day-to-day life.

E.g. 2: conservation of color charge doesn't really say anything useful about everyday processes, since it's only changed b... (read more)

The theorem guarantees the existence of a $d$-dimensional analytic manifold $M$ and a real analytic map

such that for each coordinate $M_{\alpha }$ of $M$ one can write 

I'm a bit confused here. First, I take it that $\alpha$ labels coordinate patches? Second, consider the very simple case with $d=2$ and $K\left(w\right)=w_1^2+w_2^2$. What $g$ would put $K$ into the stated form?

The peaks at 0.05 and 0.3 are strange. What regulariser did you use? Also, could you check whether all features whose nearest neighbour has cosine similarity 0.3 have the same nearest neighbour (and likewise for 0.05)?

Paging hijohnnylin -- it'd be awesome to have neuronpedia dashboards for these features. Between these, OpenAI's MLP features, and Joseph Bloom's resid_pre features, we'd have covered pretty much the whole model!

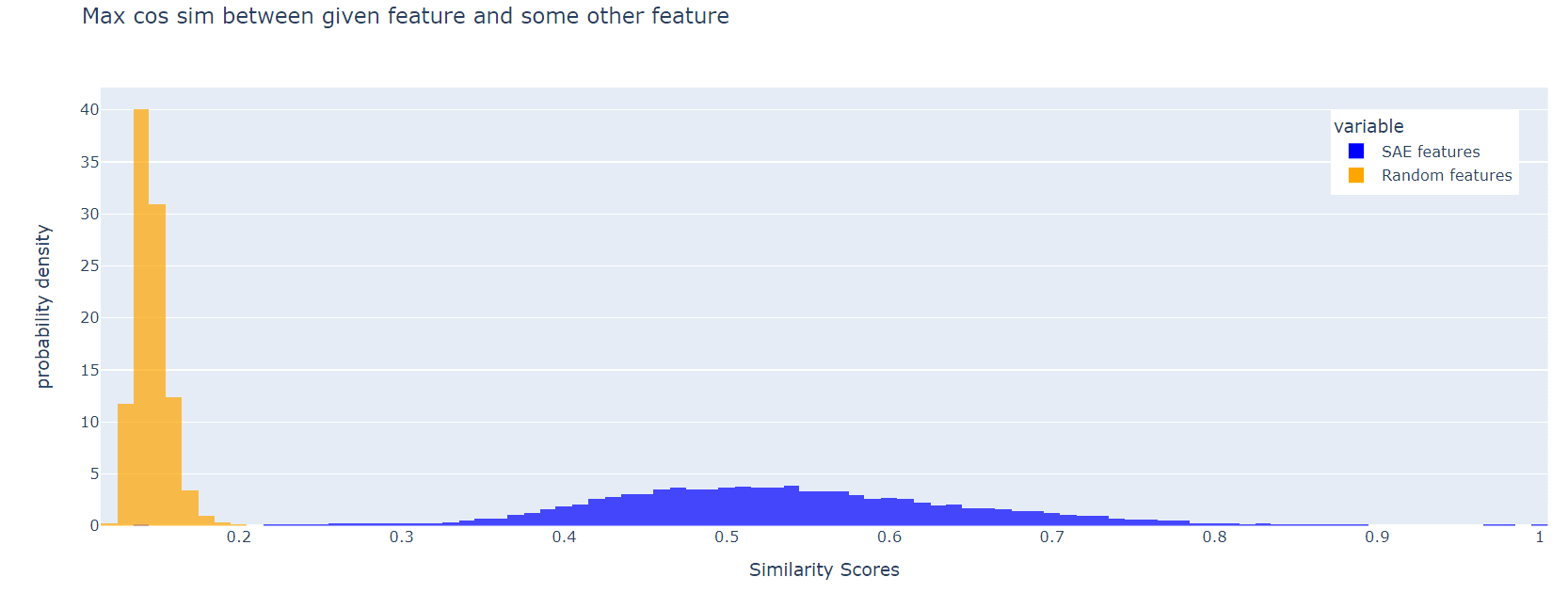
For each SAE feature (i.e. each column of W_dec), we can look for a distinct feature with the maximum cosine similarity to the first. Here is a histogram of these max cos sims, for Joseph Bloom's SAE trained at resid_pre, layer 10 in gpt2-small. The corresponding plot for random features is shown for comparison:

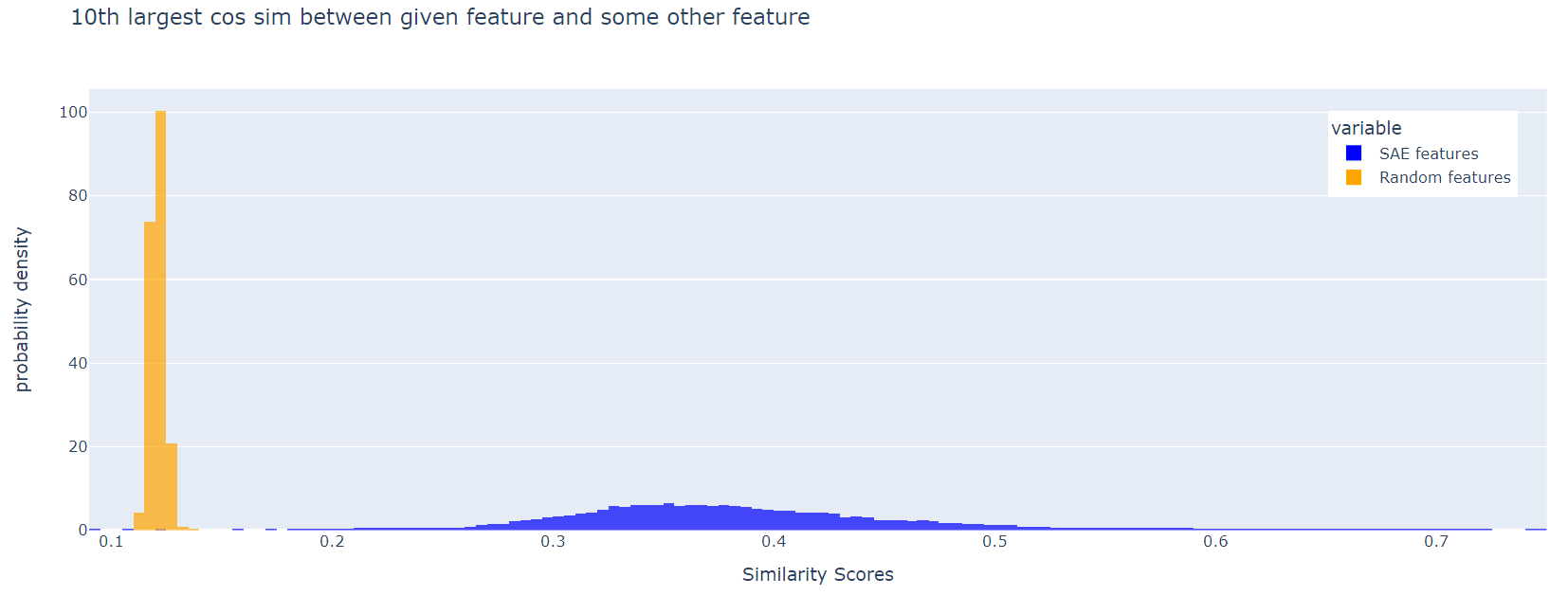
The SAE features are much less orthogonal than the random ones. This effect persists if, instead of the maximum cosine similarity, we look at the 10th largest, or the 100th largest:

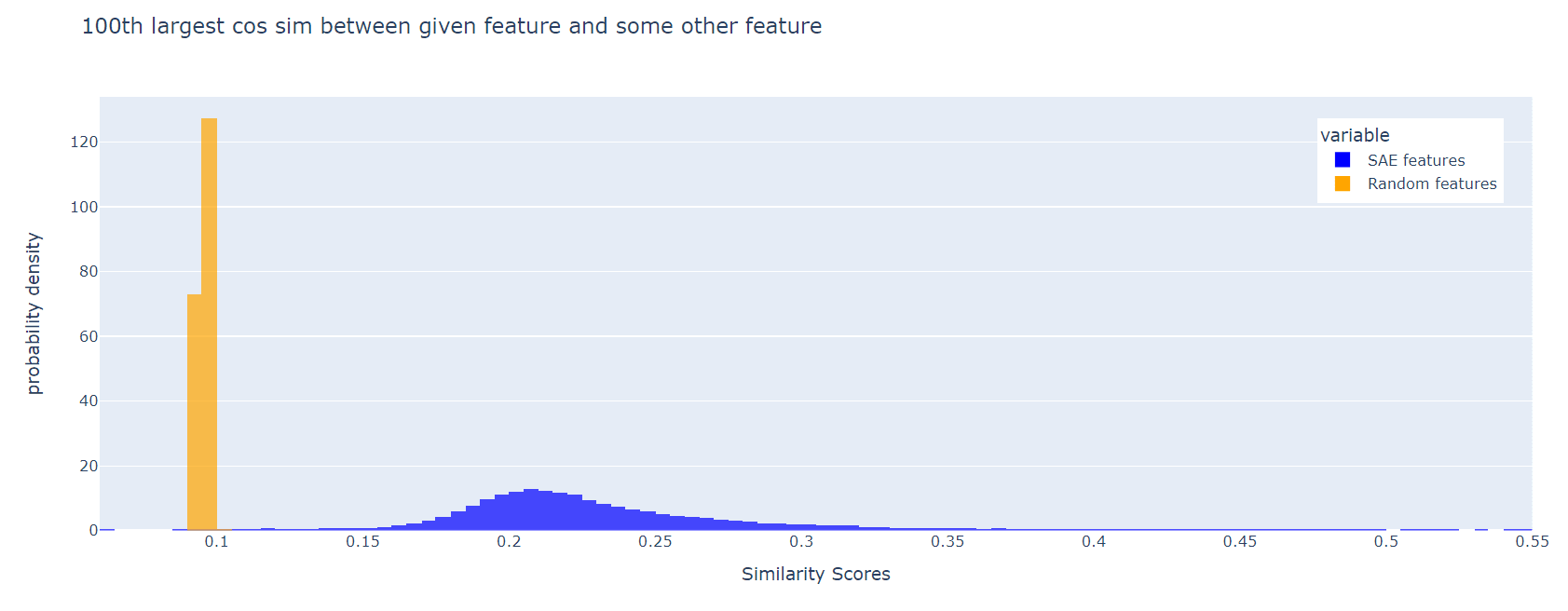
I think it's a good idea to include a loss t... (read more)

Nice, this is exactly what I was asking for. Thanks!

I'm confused about your three-dimensional example and would appreciate more mathematical detail.

Call the feature directions f1, f2, f3.

Suppose SAE hidden neurons 1,2 and 3 read off the components along f1, f2, and f1+f2, respectively. You claim that in some cases this may achieve lower L1 loss than reading off the f1, f2, f3 components.

[note: the component of a vector X along f1+f2 here refers to 1/2 * (f1+f2) \cdot X]

Can you write down the encoder biases that would achieve this loss reduction? Note that e.g. when the input is f1, there is a component of 1/2 along f1+f2, so you need a bias < -1/2 on neuron 3 to avoid screwing up the reconstruction.

Nice post. I was surprised that the model provides the same nonsense definition regardless of the token when the embedding is rescaled to be large, and moreover that this nonsense definition is very similar to the one given when the embedding is rescaled to be small. Here's an explanation I find vaguely plausible. Suppose the model completes the task as follows:

• The model sees the prompt 'A typical definition of <token> would be '. 
• At some attention head A1, the <token> position attends back to 'definition' and gains a component in the resi

I hope that type of learning isn't used

I share your hope, but I'm pessimistic. Using RL to continuously train the outer loop of an LLM agent seems like a no-brainer from a capabilities standpoint.

The alternative would be to pretrain the outer loop, and freeze the weights upon deployment. Then, I guess your plan would be to only use the independent reviewer after deployment, so that the reviewer's decision never influences the outer-loop weights. Correct me if I'm wrong here.

I'm glad you plan to address this in a future post, and I look forward to reading it.


 

I'm a little confused. What exactly is the function of the independent review, in your proposal? Are you imagining that the independent alignment reviewer provides some sort of "danger" score which is added to the loss? Or is the independent review used for some purpose other than providing a gradient signal?

I'm slightly confused about the setup. In the following, what spaces is W mapping between?

Linear: $y=Wx$

At first I expected W : R^{d_model} -> R^{d_model}. But then it wouldn't make sense to impose a sparsity penalty on W. 

In other words: what is the shape of the matrix W?

Is your issue just "Alice's first sentence is so misguided that no self-respecting safety researcher would say such a thing"? If so, I can edit to clarify the fact that this is a deliberate strawman, which Bob rightly criticises. Indeed:

Bob:  I'm asking you why models should misgeneralise in the extremely specific weird way that you mentioned

expresses a similar sentiment to Reward Is Not the Optimization Target: one should not blindly assume that models will generalise OOD to doing things that look like "maximising reward". This much is obvious by the... (read more)

Regarding 3, yeah, I definitely don't want to say that the LLM in the thought experiment is itself power-seeking. Telling someone how to power-seek is not power seeking. 

Regarding 1 and 2, I agree that the problem here is producing an LLM that refuses to give dangerous advice to another agent. I'm pretty skeptical that this can be done in a way that scales, but this could very well be lack of imagination on my part.

Define the "frequent neurons" of the hidden layer to be those that fire with frequency > 1e-4. The image of this set of neurons under W_dec forms a set of vectors living in R^d_mlp, which I'll call "frequent features". 

These frequent features are less orthogonal than I'd naively expect.

If we choose two vectors uniformly at random on the (d_mlp)-sphere, their cosine sim has mean 0 and variance 1/d_mlp = 0.0005. But in your SAE, the mean cosine sim between distinct frequent features is roughly 0.0026, and the variance is 0.002.

So the frequent feature... (read more)