Sorry I didn't get to this message earlier, glad you liked the post though! The answer is that attention heads can have multiple different functions - the simplest way is to store things entirely orthogonally so they lie in fully independent subspsaces, but even this isn't necessary because it seems like transformers take advantage of superposition to represent multiple concepts at once, more so than they have dimensions.
Oh, interesting, wasn't aware of this bug. I guess this is probably fine since most people replicating it will be pulling it rather than copying and pasting it into their IDE. Also this comment thread is now here for anyone who might also get confused. Thanks for clarifying!
+1, thanks for sharing! I think there's a formatting error in the notebook, where the tags like <OUTPUT> were all removed and replaced with empty strings (e.g. see attached photo). We've recently made the ARENA evals material public, and we've got a working replication there which I think has the tags in the right place (section 2 of 3 on the page linked here)
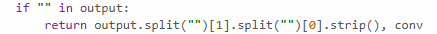
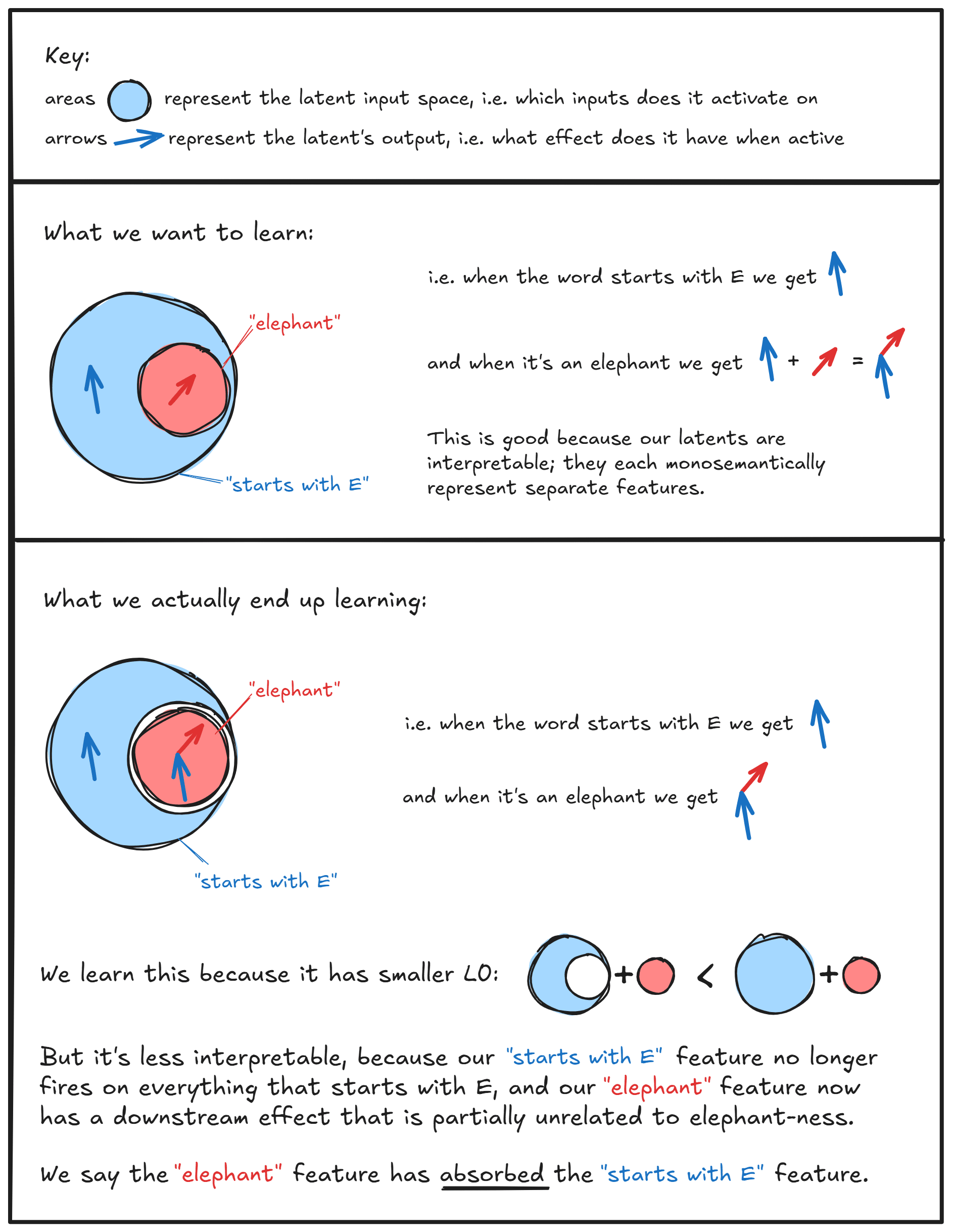
Amazing post! Forgot to do this for a while, but here's a linked diagram explaining how I think about feature absorption, hopefully ppl find it helpful!
I don't know of specific examples, but this is the image I have in my head when thinking about why untied weights are more free than tied weights:
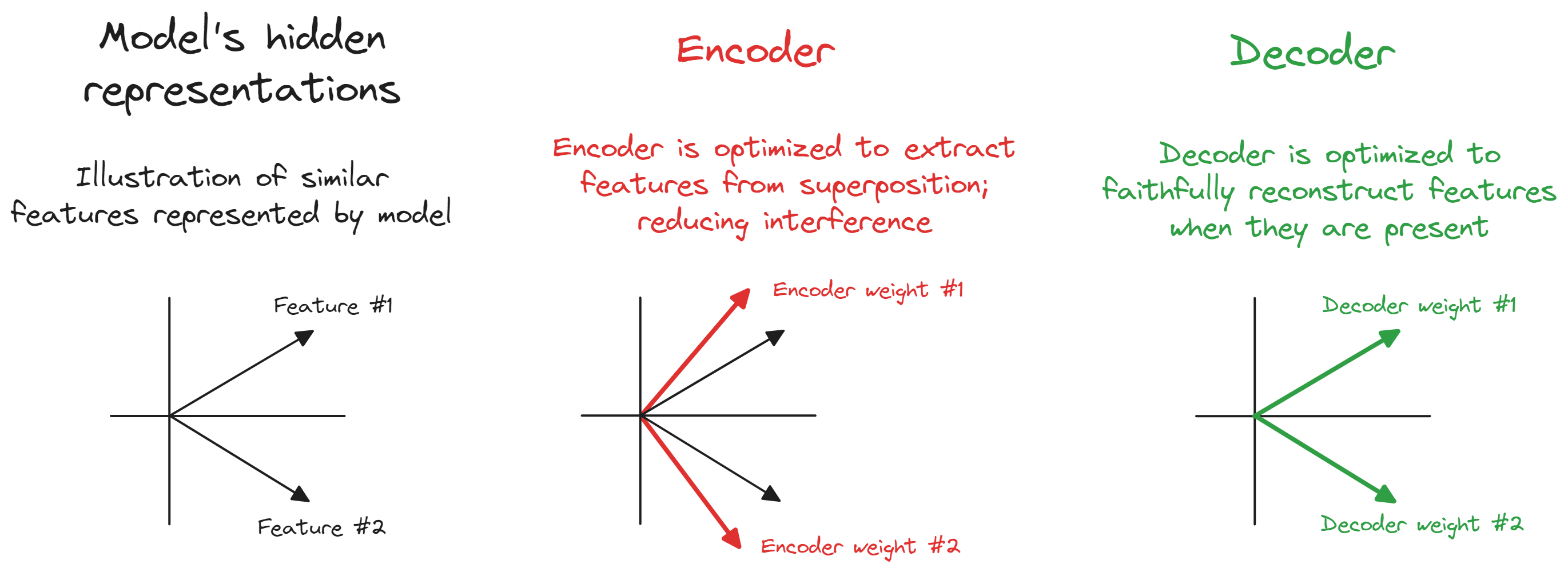
I think more generally this is why I think studying SAEs in the TMS setup can be a bit challenging, because there's often too much symmetry and not enough complexity for untied weights to be useful, meaning just forcing your weights to be tied can fix a lot of problems! (We include it in ARENA mostly for illustration of key concepts, not because it gets you many super informative results). But I'm keen for more work like this trying to understand feature absorption better in more tractible cases
Oh yeah this is great, thanks! For people reading this, I'll highlight SLT + developmental interp + mamba as areas which I think are large enough to have specific exercise sections but currently don't
Thanks!! Really appreciate it
Thanks so much! (-:
Thanks so much, really glad to hear it's been helpful!
True, although I wish more people would engage with the common anti-AI-x-risk argument of "tech CEOs are exaggerating existential risk because they think it'll make their products seem more important and potentially world changing, and so artificially boost hype". Not saying I agree with this, but there's at least some extent to which it's true, and I think this community often fails to appropriately engage with and combat this argument.
In general, this is why "appeal to authority" arguments should generally be avoided if we're talking about people who are widely seen as untrustworthy and having ulterior motives. At most I think people like Geoffrey Hinton are seen as reputable and not as morally compromised so serve as better subjects for an appeal to authority, but mostly rather than needing to appeal to authority at all we should just try and bring things back to the object-level arguments.