This is a special post for quick takes by Mo Putera. Only they can create top-level comments. Comments here also appear on the Quick Takes page and All Posts page.
Interesting anecdote on "von Neumann's onion" and his general style, from P. R. Halmos' The Legend of John von Neumann:
...Style. As a writer of mathematics von Neumann was clear, but not clean; he was powerful but not elegant. He seemed to love fussy detail, needless repetition, and notation so explicit as to be confusing. To maintain a logically valid but perfectly transparent and unimportant distinction, in one paper he introduced an extension of the usual functional notation: along with the standard φ(x) he dealt also with something denoted by φ((x)). The hair that was split to get there had to be split again a little later, and there was φ(((x))), and, ultimately, φ((((x)))). Equations such as
(φ((((a))))^2 = φ(((a))))
have to be peeled before they can be digested; some irreverent students referred to this paper as von Neumann’s onion.
Perhaps one reason for von Neumann’s attention to detail was that he found it quicker to hack through the underbrush himself than to trace references and see what others had done. The result was that sometimes he appeared ignorant of the standard literature. If he needed facts, well-known facts, from Lebesgue integration theory, he waded in, defi
I have this experience with @ryan_greenblatt -- he's got an incredible ability to keep really large and complicated argument trees in his head, so he feels much less need to come up with slightly-lossy abstractions and categorizations than e.g. I do. This is part of why his work often feels like huge, mostly unstructured lists. (The lists are more unstructured before his pre-release commenters beg him to structure them more.) (His code often also looks confusing to me, for similar reasons.)
1While Dyson's birds and frogs archetypes of mathematicians is oft-mentioned, David Mumford's tribes of mathematicians is underappreciated, and I find myself pointing to it often in discussions that devolve into "my preferred kind of math research is better than yours"-type aesthetic arguments:
...... the subjective nature and attendant excitement during mathematical activity, including a sense of its beauty, varies greatly from mathematician to mathematician... I think one can make a case for dividing mathematicians into several tribes depending on what most strongly drives them into their esoteric world. I like to call these tribes explorers, alchemists, wrestlers and detectives. Of course, many mathematicians move between tribes and some results are not cleanly part the property of one tribe.
- Explorers are people who ask -- are there objects with such and such properties and if so, how many? They feel they are discovering what lies in some distant mathematical continent and, by dint of pure thought, shining a light and reporting back what lies out there. The most beautiful things for them are the wholly new objects that they discover (the phrase 'bright shiny objects' has been i
4Scott Alexander's Mistakes, Dan Luu's Major errors on this blog (and their corrections), Gwern's My Mistakes (last updated 11 years ago), and Nintil's Mistakes (h/t @Rasool) are the only online writers I know of who maintain a dedicated, centralized page solely for cataloging their errors, which I admire. Probably not coincidentally they're also among the thinkers I respect the most for repeatedly empirically grounding their reasoning. Some orgs do this too, like 80K's Our mistakes, CEA's Mistakes we've made, and GiveWell's Our mistakes.
While I prefer dedicated centralized pages like those to one-off writeups for long content benefit reasons, one-off definitely beats none (myself included). In that regard I appreciate essays like Holden Karnofsky's Some Key Ways in Which I've Changed My Mind Over the Last Several Years (2016), Denise Melchin's My mistakes on the path to impact (2020), Zach Groff's Things I've Changed My Mind on This Year (2017), Michael Dickens' things I've changed my mind on, and this 2013 LW repository for "major, life-altering mistakes that you or others have made", as well as by orgs like HLI's Learning from our mistakes.
In this vein I'm also sad to see m...
17
I'm not convinced Scott Alexander's mistakes page accurately tracks his mistakes. E.g. the mistake on it I know the most about is this one:
But that's basically wrong. The study found women's arousal to chimps having sex to be very close to their arousal to nonsexual stimuli, and far below their arousal to sexual stimuli.
1
Thanks, good example.
4
I don't have a mistakes page but last year I wrote a one-off post of things I've changed my mind on.
2
Thanks Michael. On another note, I've recommended some of your essays to others, so thanks for writing them as well.
2
I'm glad to hear that! I often don't hear much response to my essays so it's good to know you've read some of them :)
2
You're welcome :) in particular, your 2015 cause selection essay was I thought a particularly high-quality writeup of the end-to-end process from personal values to actual donation choice and (I appreciated this) where you were most likely to change your mind, so I recommended it to a few folks as well as used it as a template myself back in the day.
In general I think theory-practice gap bridging via writeups like those are undersupplied, especially the end-to-end ones — more writeups bridge parts of the "pipeline", but "full pipeline integration" done well is rare and underappreciated, which combined with how effortful it is to do it makes me not surprised there isn't more of it.
4
Another good blog:
https://nintil.com/mistakes
1
Thanks! Added to the list.
What fraction of economically-valuable cognitive labor is already being automated today? How has that changed over time, especially recently?
I notice I'm confused about these ostensibly extremely basic questions, which arose in reading Open Phil's old CCF-takeoff report, whose main metric is "time from AI that could readily[2] automate 20% of cognitive tasks to AI that could readily automate 100% of cognitive tasks". A cursory search of Epoch's data, Metaculus, and this forum didn't turn up anything, but I didn't spend much time at all doing so.
I was originally motivated by wanting to empirically understand recursive AI self-improvement better, which led to me stumbling upon the CAIS paper Examples of AI Improving AI, but I don't have any sense whatsoever of how the paper's 39 examples as of Oct-2023 translate to OP's main metric even after constraining "cognitive tasks" in its operational definition to just AI R&D.
I did find this 2018 survey of expert opinion
...A survey was administered to attendees of three AI conferences during the summer of 2018 (ICML, IJCAI and the HLAI conference). The survey included questions for estimating AI capabilities over the next d
3
Did e.g. a telephone operator in 1910 perform cognitive labor, by the definition we want to use here?
1
I'm mainly wondering how Open Phil, and really anyone who uses fraction of economically-valuable cognitive labor automated / automatable (e.g. the respondents to that 2018 survey; some folks on the forum) as a useful proxy for thinking about takeoff, tracks this proxy as a way to empirically ground their takeoff-related reasoning. If you're one of them, I'm curious if you'd answer your own question in the affirmative?
2
I am not one of them - I was wondering the same thing, and was hoping you had a good answer.
If I was trying to answer this question, I would probably try to figure out what fraction of all economically-valuable labor each year was cognitive, the breakdown of which tasks comprise that labor, and the year-on-year productivity increases on those task, then use that to compute the percentage of economically-valuable labor that is being automated that year.
Concretely, to get a number for the US in 1900 I might use a weighted average of productivity increases across cognitive tasks in 1900, in an approach similar to how CPI is computed
* Look at the occupations listed in the 1900 census records
* Figure out which ones are common, and then sample some common ones and make wild guesses about what those jobs looked like in 1900
* Classify those tasks as cognitive or non-cognitive
* Come to estimate that record-keeping tasks are around a quarter to a half of all cognitive labor
* Notice that typewriters were starting to become more popular - about 100,000 typewriters sold per year
* Note that those 100k typewriters were going to the people who would save the most time by using them
* As such, estimate 1-2% productivity growth in record-keeping tasks in 1900
* Multiply the productivity growth for record-keeping tasks by the fraction of time (technically actually 1-1/productivity increase but when productivity increase is small it's not a major factor)
* Estimate that 0.5% of cognitive labor was automated by specifically typewriters in 1900
* Figure that's about half of all cognitive labor automation in 1900
and thus I would estimate ~1% of all cognitive labor was automated in 1900. By the same methodology I would probably estimate closer to 5% for 2024.
Again, though, I am not associated with Open Phil and am not sure if they think about cognitive task automation in the same way.
I chose to study physics in undergrad because I wanted to "understand the universe" and naively thought string theory was the logically correct endpoint of this pursuit, and was only saved from that fate by not being smart enough to get into a good grad school. Since then I've come to conclude that string theory is probably a dead end, albeit an astonishingly alluring one for a particular type of person. In that regard I find anecdotes like the following by Ron Maimon on Physics SE interesting — the reason string theorists believe isn’t the same as what they tell people, so it’s better to ask for their conversion stories:
...I think that it is better to ask for a compelling argument that the physics of gravity requires a string theory completion, rather than a mathematical proof, which would be full of implicit assumptions anyway. The arguments people give in the literature are not the same as the personal reasons that they believe the theory, they are usually just stories made up to sound persuasive to students or to the general public. They fall apart under scrutiny. The real reasons take the form of a conversion story, and are much more subjective, and much less persuasive to everyo
In pure math, mathematicians seek "morality", which sounds similar to Ron's string theory conversion stories above. Eugenia Cheng's Mathematics, morally argues:
...I claim that although proof is what supposedly establishes the undeniable truth of a piece of mathematics, proof doesn’t actually convince mathematicians of that truth. And something else does.
... formal mathematical proofs may be wonderfully watertight, but they are impossible to understand. Which is why we don’t write whole formal mathematical proofs. ... Actually, when we write proofs what we have to do is convince the community that it could be turned into a formal proof. It is a highly sociological process, like appearing before a jury of twelve good men-and-true. The court, ultimately, cannot actually know if the accused actually ‘did it’ but that’s not the point; the point is to convince the jury. Like verdicts in court, our ‘sociological proofs’ can turn out to be wrong—errors are regularly found in published proofs that have been generally accepted as true. So much for mathematical proof being the source of our certainty. Mathematical proof in practice is certainly fallible.
But this isn’t the only
6
The more you know about particle physics and quantum field theory, the more inevitable string theory seems. There are just too many connections. However, identifying the specific form of string theory that corresponds to our universe is more of a challenge, and not just because of the fabled 10^500 vacua (though it could be one of those). We don't actually know either all the possible forms of string theory, or the right way to think about the physics that we can see. The LHC, with its "unnaturally" light Higgs boson, already mortally wounded a particular paradigm for particle physics (naturalness) which in turn was guiding string phenomenology (i.e. the part of string theory that tries to be empirically relevant). So along with the numerical problem of being able to calculate the properties of a given string vacuum, the conceptual side of string theory and string phenomenology is still wide open for discovery.
9
I asked a well-known string theorist about the fabled 10^500 vacua and asked him whether he worried that this would make string theory a vacuous theory since a theory that fits anything fits nothing. He replied ' no, no the 10^500 'swampland' is a great achievement of string theory - you see... all other theories have infinitely many adjustable parameters'. He was saying string theory was about ~1500 bits away from the theory of everything but infinitely ahead of its competitors.
Diabolical.
Much ink has been spilled on the scientific merits and demerits of string theory and its competitors. The educated reader will recognize that this all this and more is of course, once again, solved by UDASSA.
2
Re other theories, I don't think that all other theories in existence have infinitely many adjustable parameters, and if he's referring to the fact that lots of theories have adjustable parameters that can range over the real numbers, which are infinitely complicated in general, than that's different, and string theory may have this issue as well.
Re string theory's issue of being vacuous, I think the core thing that string theory predicts that other quantum gravity models don't is that at the large scale, you recover general relativity and the standard model, whereas no other theory can yet figure out a way to properly include both the empirical effects of gravity and quantum mechanics in the parameter regimes where they are known to work, so string theory predicts more just by predicting the things other quantum mechanics predicts while having the ability to include in gravity without ruining the other predictions, whereas other models of quantum gravity tend to ruin empirical predictions like general relativity approximately holding pretty fast.
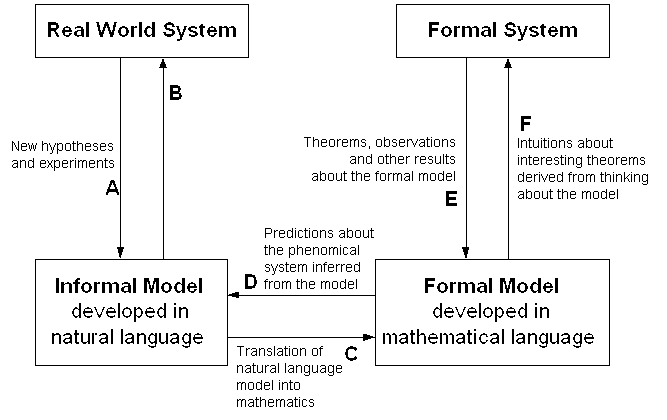
I used to consider it a mystery that math was so unreasonably effective in the natural sciences, but changed my mind after reading this essay by Eric S. Raymond (who's here on the forum, hi and thanks Eric), in particular this part, which is as good a question dissolution as any I've seen:
The relationship between mathematical models and phenomenal prediction is complicated, not just in practice but in principle. Much more complicated because, as we now know, there are mutually exclusive ways to axiomatize mathematics! It can be diagrammed as follows (thanks to Jesse Perry for supplying the original of this chart):
(it's a shame this chart isn't rendering properly for some reason, since without it the rest of Eric's quote is ~incomprehensible)
...The key transactions for our purposes are C and D -- the translations between a predictive model and a mathematical formalism. What mystified Einstein is how often D leads to new insights.
We begin to get some handle on the problem if we phrase it more precisely; that is, "Why does a good choice of C so often yield new knowledge via D?"
The simplest answer is to invert the question and treat it as a definition. A "good choi
6
Interesting. This reminds me of a related thought I had: Why do models with differential equations work so often in physics but so rarely in other empirical sciences? Perhaps physics simply is "the differential equation science".
Which is also related to the frequently expressed opinion that philosophy makes little progress because everything that gets developed enough to make significant progress splits off from philosophy. Because philosophy is "the study of ill-defined and intractable problems".
Not saying that I think these views are accurate, though they do have some plausibility.
1
(To be honest, to first approximation my guess mirrors yours.)
3
Flagging that those two examples seem false. The weather is chaotic, yes, and there's a sense in which the economy is anti-inductive, but modeling methods are advancing, and will likely find more loop-holes in chaos theory.
For example, in thermodynamics, temperature is non-chaotic while the precise kinetic energies and locations of all particles are. A reasonable candidate similarity in weather are hurricanes.
Similarly as our understanding of the economy advances it will get more efficient which means it will be easier to model. eg (note: I've only skimmed this paper). And definitely large economies are even more predictable than small villages, talk about not having a competitive market!
3
Thanks for the pointer to that paper, the abstract makes me think there's a sort of slow-acting self-reinforcing feedback loop between predictive error minimisation via improving modelling and via improving the economy itself.
re: weather, I'm thinking of the chart below showing how little gain we get in MAE vs compute, plus my guess that compute can't keep growing far enough to get MAE < 3 °F a year out (say). I don't know anything about advancements in weather modelling methods though; maybe effective compute (incorporating modelling advancements) may grow indefinitely in terms of the chart.
2
I didn't say anything about temperature prediction, and I'd also like to see any other method (intuition based or otherwise) do better than the current best mathematical models here. It seems unlikely to me that the trends in that graph will continue arbitrarily far.
Yeah, that was my claim.
3
I would also comment that, if the environment was so chaotic that roughly everything important to life could not be modeled—if general-purpose modeling ability was basically useless—then life would not have evolved that ability, and "intelligent life" probably wouldn't exist.
2
The two concepts that I thought were missing from Eliezer's technical explanation of technical explanation that would have simplified some of the explanation were compression and degrees of freedom. Degrees of freedom seems very relevant here in terms of how we map between different representations. Why are representations so important for humans? Because they have different computational properties/traversal costs while humans are very computationally limited.
1
Can you say more about what you mean? Your comment reminded me of Thomas Griffiths' paper Understanding Human Intelligence through Human Limitations, but you may have meant something else entirely.
Griffiths argued that the aspects we associate with human intelligence – rapid learning from small data, the ability to break down problems into parts, and the capacity for cumulative cultural evolution – arose from the 3 fundamental limitations all humans share: limited time, limited computation, and limited communication. (The constraints imposed by these characteristics cascade: limited time magnifies the effect of limited computation, and limited communication makes it harder to draw upon more computation.) In particular, limited computation leads to problem decomposition, hence modular solutions; relieving the computation constraint enables solutions that can be objectively better along some axis while also being incomprehensible to humans.
3
Thanks for the link. I mean that predictions are outputs of a process that includes a representation, so part of what's getting passed back and forth in the diagram are better and worse fit representations. The degrees of freedom point is that we choose very flexible representations, whittle them down with the actual data available, then get surprised that that representation yields other good predictions. But we should expect this if Nature shares any modular structure with our perception at all, which it would if there was both structural reasons (literally same substrate) and evolutionary pressure for representations with good computational properties i.e. simple isomorphisms and compressions.
1
Matt Leifer, who works in quantum foundations, espouses a view that's probably more extreme than Eric Raymond's above to argue why the effectiveness of math in the natural sciences isn't just reasonable but expected-by-construction. In his 2015 FQXi essay Mathematics is Physics Matt argued that
(Matt notes as an aside that he's arguing for precisely the opposite of Tegmark's MUH.)
Why "scale-free network"?
As an aside, Matt's theory of theory-building explains (so he claims) what mathematical intuition is about: "intuition for efficient knowledge structure, rather than intuition about an abstract mathematical world".
So what? How does this view pay rent?
Matt further develops the argument that the structure of human knowledge being networked-not-hierarchical implies that the idea that there is a most fundamental discipline, or level of reality, is mistaken in Against Fundamentalism, another FQXi essay published in 2018.
This remark at 16:10 by Dwarkesh Patel on his most recent podcast interview AMA: Career Advice Given AGI, How I Research ft. Sholto & Trenton was pretty funny:
... big guests just don't really matter that much if you just look at what are the most popular episodes, or what in the long run helps a podcast grow. By far my most popular guest is Sarah Paine, and she, before I interviewed her, was just a scholar who was not publicly well-known at all, and I just found her books quite interesting—so my most popular guests are Sarah Paine and then Sarah Paine, Sarah Paine, Sarah Paine because I have
electric chairs(?)a lecture series with her. And by the way, from a viewer-a-minute adjusted basis, I host the Sarah Paine podcast where I occasionally talk about AI.
(After Sarah Paine comes geneticist David Reich, then Satya Nadella and Mark Zuckerberg, "then [Sholto & Trenton] or Leopold (Aschenbrenner) or something, then you get to the lab CEOs or something")
3You can see it as an example of 'alpha' vs 'beta'. When someone asks me about the value of someone as a guest, I tend to ask: "do they have anything new to say? didn't they just do a big interview last year?" and if they don't but they're big, "can you ask them good questions that get them out of their 'book'?" Big guests are not necessarily as valuable as they may seem because they are highly-exposed, which means both that (1) they have probably said everything they will said before and there is no 'news' or novelty, and (2) they are message-disciplined and careful to "talk their book". (In this analogy, "alpha" represents undiscovered or neglected interview topics which can be extracted mostly just by finding it and then asking the obvious question, usually by interviewing new people; "beta" represents doing standard interview topics/people, but much more so - harder, faster, better - and getting new stuff that way.)
Lex Fridman podcasts are an example of this: he often hosts very big guests like Mark Zuckerberg, but nevertheless, I will sit down and skim through the transcript of 2-4 hours of content, and find nothing even worth excerpting for my notes. Fridman notoriously does n...
3
I like the optimal forager take, seems intuitively correct. I'd add that Dwarkesh struck gold by getting you on his podcast too. (Tangentially: this grand theory of intelligence video snippet reminds me of a page-ish-long writeup on that I stumbled upon deep in the bowels of https://gwern.net/ which I've annoyingly never been able to find again.)
Also thanks for the pointer to Werbos, his website Welcome to the Werbos World! funnily enough struck me as crackpot-y and I wouldn't have guessed just from the landing page that he's the discoverer of backprop, respected former program director at the NSF, etc.
7
Probably https://gwern.net/newsletter/2021/05#master-synthesis
That's what makes it alpha! If he was as legible as, say, Hinton, he would be mined out by now, and nothing but beta. (Similar situation to Schmidhuber - 'obvious crackpot' - although he's such a self-promoter that he overcomes it, and so at this point there's no alpha talking to him; the stuff that would be interesting, like his relationship to certain wealthy Italians, or to King Bonesaws, or how he's managed to torpedo his career so spectacularly, he will not talk about. Also, I understand he likes to charge people for the privilege of talking to him.) You have to have both domain knowledge and intellectual courage to know about Werbos and eg. read his old interviews and be willing to go out on a limb and interview him.
2
This seems to underrate the value of distribution. I suspect another factor to take into account is the degree of audience overlap. Like there's a lot of value in booking a guest who has been on a bunch of podcasts, so long as your particular audience isn't likely to have been exposed to them.
2
I’d guess that was “I have a lecture series with her” :-)
1
D'oh, you're obviously right, thanks!
Unbundling Tools for Thought is an essay by Fernando Borretti I found via Gwern's comment which immediately resonated with me (emphasis mine):
...I’ve written something like six or seven personal wikis over the past decade. It’s actually an incredibly advanced form of procrastination1. At this point I’ve tried every possible design choice.
Lifecycle: I’ve built a few compiler-style wikis: plain-text files in a
gitrepo statically compiled to HTML. I’ve built a couple using live servers with server-side rendering. The latest one is an API server with a React frontend.Storage: I started with plain text files in a git repo, then moved to an SQLite database with a simple schema. The latest version is an avant-garde object-oriented hypermedia database with bidirectional links implemented on top of SQLite.
Markup: I used Markdown here and there. Then I built my own TeX-inspired markup language. Then I tried XML, with mixed results. The latest version uses a WYSIWYG editor made with ProseMirror.
And yet I don’t use them. Why? Building them was fun, sure, but there must be utility to a personal database.
At first I thought the problem was friction: the higher the activation energy to u
4
Minimizing friction is surprisingly difficult. I keep plain-text notes in a hierarchical editor (cherrytree), but even that feels too complicated sometimes. This is not just about the tool... what you actually need is a combination of the tool and the right way to use it.
(Every tool can be used in different ways. For example, suppose you write a diary in MS Word. There are still options such as "one document per day" or "one very long document for all", and things in between like "one document per month", which all give different kinds of friction. The one megadocument takes too much time to load. It is more difficult to search in many small documents. Or maybe you should keep your current day in a small document, but once in a while merge the previous days into the megadocument? Or maybe switch to some application that starts faster than MS Word?)
Forgetting is an important part. Even if you want to remember forever, you need some form of deprioritizing. Something like "pages you haven't used for months will get smaller, and if you search for keywords, they will be at the bottom of the result list". But if one of them suddenly becomes relevant again, maybe the connected ones become relevant, too? Something like associations in brain. The idea is that remembering the facts is only a part of the problem; making the relevant ones more accessible is another. Because searching in too much data is ultimately just another kind of friction.
It feels like a smaller version of the internet. Years ago, the problem used to be "too little information", now the problem is "too much information, can't find the thing I actually want".
Perhaps a wiki, where the pages could get flagged as "important now" and "unimportant"? Or maybe, important for a specific context? And by default, when you choose a context, you would only see the important pages, and the rest of that only if you search for a specific keyword or follow a grey link. (Which again would require some work creating
2
@dkl9 wrote a very eloquent and concise piece arguing in favor of ditching "second brain" systems in favor of SRSs (Spaced Repetition Systems, such as Anki).
2
I like to think of learning and all of these things as self-contained smaller self-contained knowledge trees. Building knowledge trees that are cached, almost like creatin zip files and systems where I store a bunch of zip files similar to what Elizier talks about in The Sequences.
Like when you mention the thing about Nielsen on linear algebra it opens up the entire though tree there. I might just get the association to something like PCA and then I think huh, how to ptimise this and then it goes to QR-algorithms and things like a householder matrix and some specific symmetric properties of linear spaces...
If I have enough of these in an area then I might go back to my anki for that specific area. Like if you think from the perspective of schedulling and storage algorithms similar to what is explored in algorithms to live by you quickly understand that the magic is in information compression and working at different meta-levels. Zipped zip files with algorithms to expand them if need be. Dunno if that makes sense, agree with the exobrain creep that exists though.
I currently work in policy research, which feels very different from my intrinsic aesthetic inclination, in a way that I think Tanner Greer captures well in The Silicon Valley Canon: On the Paıdeía of the American Tech Elite:
...I often draw a distinction between the political elites of Washington DC and the industrial elites of Silicon Valley with a joke: in San Francisco reading books, and talking about what you have read, is a matter of high prestige. Not so in Washington DC. In Washington people never read books—they just write them.
To write a book, of course, one must read a good few. But the distinction I drive at is quite real. In Washington, the man of ideas is a wonk. The wonk is not a generalist. The ideal wonk knows more about his or her chosen topic than you ever will. She can comment on every line of a select arms limitation treaty, recite all Chinese human rights violations that occurred in the year 2023, or explain to you the exact implications of the new residential clean energy tax credit—but never all at once. ...
Washington intellectuals are masters of small mountains. Some of their peaks are more difficult to summit than others. Many smaller slopes are nonetheless ja
I enjoyed Brian Potter's Energy infrastructure cheat sheet tables over at Construction Physics, it's a great fact post. Here are some of Brian's tables — if they whet your appetite, do check out his full essay.
Energy quantities:
Units and quantities | Kilowatt-hours | Megawatt-hours | Gigawatt-hours |
|---|---|---|---|
| 1 British Thermal Unit (BTU) | 0.000293 | ||
| iPhone 14 battery | 0.012700 | ||
| 1 pound of a Tesla battery pack | 0.1 | ||
| 1 cubic foot of natural gas | 0.3 | ||
| 2000 calories of food | 2.3 | ||
| 1 pound of coal | 2.95 | ||
| 1 gallon of milk (calorie value) | 3.0 | ||
| 1 gallon of gas | 33.7 | ||
| Tesla Model 3 standard battery pack | 57.5 | ||
| Typical ICE car gas tank (15 gallons) | 506 | ||
| 1 ton of TNT | 1,162 | ||
| 1 barrel of oil | 1,700 | ||
| 1 ton of oil | 11,629 | 12 | |
| Tanker truck full of gasoline (9300 gallons) | 313,410 | 313 | |
| LNG carrier (180,000 cubic meters) | 1,125,214,740 | 1,125,215 | 1,125 |
| 1 million tons of TNT (1 megaton) | 1,162,223,152 | 1,162,223 | 1,162 |
| Oil supertanker (2 million barrels) | 3,400,000,000 | 3,400,000 | 3,400 |
It's amazing that a Tesla Model 3's standard battery pack has an OOM less energy capacity than a typical 15-gallon ICE car gas tank, and is probably heavier to...
Pilish is a constrained writing style where the number of letters in consecutive words match the digits of pi. The canonical intro-to-Pilish sentence is "How I need a drink, alcoholic of course, after the heavy lectures involving quantum mechanics!"; my favorite Pilish poetry is Mike Keith's Near a Raven, a retelling of Edgar Allan Poe's "The Raven" stretching to 740 digits of pi (nowhere near Keith's longest, that would be the 10,000-word world record-setting Not a Wake), which begins delightfully like so:
...Poe, E.
Near a RavenMidnights
17
I asked GPT 4.5 to write a system prompt and user message for models to write Pilish poems, feeding it your comment as context.
Then I gave these prompts to o1 (via OpenAI's playground).
GPT 4.5's system prompt
You are an expert composer skilled in writing poetry under strict, unusual linguistic constraints, specifically "Pilish." Pilish is a literary constraint in which the length of consecutive words precisely matches each digit of π (pi). The first word contains 3 letters, second word 1 letter, third word 4 letters, fourth word 1 letter, fifth word 5 letters, sixth word 9 letters, and so forth, accurately reflecting the sequence of pi’s digits.
For example, the classic Pilish sentence is:
"How I need a drink, alcoholic of course, after the heavy lectures involving quantum mechanics!"
As another reference, Mike Keith famously wrote a poem titled "Near a Raven," a Pilish version of Edgar Allan Poe's "The Raven," precisely encoding hundreds of pi digits into elegant verse.
Important guidelines:
You must strictly adhere to the Pilish constraint without exception or deviation.
Carefully recount each word to match each digit exactly.
Maintain coherence, clarity, and literary quality in your writing.
Make sure the poem or text is meaningful, evocative, creative, and intriguing, not just mechanically correct.
Verify each word length explicitly to ensure compliance with Pilish.
Your task is to craft a compelling, original poem in Pilish form. Do not explain the poem afterward; the precision and artistry of the piece itself is sufficient.
--
GPT 4.5's user message
Write an original Pilish poem about pi itself: reflecting upon the wonder, mystery, and endless fascination humans have felt over millennia towards this famous mathematical constant. Make it vivid, thoughtful, and meticulously correct in matching the Pilish constraint. Begin now.
--
o1's completion
I asked o1 to count the letters in each word, comparing with pi:
And this seems correct!
2
This is great, thanks! Didn't think of the model-prompting-model trick.
4
LLMs use tokens instead of letters, so counting letters is sufficiently unnatural to them relative to their other competencies that I don't see much value in directly asking LLMs to do this kind of thing. At least give them some basic scaffolding, like a full English dictionary with a column which explicitly indicates respective word lengths. In particular, the Gemini models have a context window of 1M tokens, which should be enough to fit most of the Oxford English Dictionary in there (since it includes 171k words which are in current use).
4
I think I failed to implicitly convey that I meant all this in jest, that I get a lot of personal enjoyment value out of silly poetry constrained by artificial rules, and that I was guessing at least someone else on the forum would share this enjoyment. I do like your scaffolding idea, might just try it out.
From Brian Potter's Construction Physics newsletter I learned about Taara, framed as "Google's answer to Starlink" re: remote internet access, using ground-based optical communication instead of satellites ("fiber optics without the fibers"; Taara calls them "light bridges"). I found this surprising. Even more surprisingly, Taara isn't just a pilot but a moneymaking endeavor if this Wired passage is true:
...Taara is now a commercial operation, working in more than a dozen countries. One of its successes came in crossing the Congo River. On one side was Brazza
Peter Watts' 2006 novel Blindsight has this passage on what it's like to be a "scrambler", superintelligent yet nonsentient (in fact superintelligent because it's unencumbered by sentience), which I read a ~decade ago and found unforgettable:
...Imagine you're a scrambler.
Imagine you have intellect but no insight, agendas but no awareness. Your circuitry hums with strategies for survival and persistence, flexible, intelligent, even technological—but no other circuitry monitors it. You can think of anything, yet are conscious of nothing.
You can't imagine such a
3
It's very funny that Rorschach linguistic ability is totally unremarkable comparing to modern LLMs.
3
How interesting, I was curious about copyright etc but this is annotated by the author himself!
Ravi Vakil's advice for potential PhD students includes this bit on "tendrils to be backfilled" that's stuck with me ever since as a metaphor for deepening understanding over time:
...Here's a phenomenon I was surprised to find: you'll go to talks, and hear various words, whose definitions you're not so sure about. At some point you'll be able to make a sentence using those words; you won't know what the words mean, but you'll know the sentence is correct. You'll also be able to ask a question using those words. You still won't know what the words mean, but yo
Out of curiosity — how relevant is Holden's 2021 PASTA definition of TAI still to the discourse and work on TAI, aside from maybe being used by Open Phil (not actually sure that's the case)? Any pointers to further reading, say here or on AF etc?
...AI systems that can essentially automate all of the human activities needed to speed up scientific and technological advancement. I will call this sort of technology Process for Automating Scientific and Technological Advancement, or PASTA.3 (I mean PASTA to refer to either a single system or a collection of system
When I first read Hannu Rajaniemi's Quantum Thief trilogy c. 2015 I had two reactions: delight that this was the most my-ingroup-targeted series I had ever read, and a sinking feeling that ~nobody else would really get it, not just the critics but likely also most fans, many of whom would round his carefully-chosen references off to technobabble. So I was overjoyed to recently find Gwern's review of it, which Hannu affirms "perfectly nails the emotional core of the trilogy and, true to form, spots a number of easter eggs I thought no one would ever find", ...
3
The parts of the science I understand were all quite plausible (mind duplication/fractioning and motivations for doing so).
Beyond the accuracy of the science, this was one of the most staggeringly imaginative and beautifully written scifi books I've ever read. It's for a very particular audience, but if you're here you might be that audience. If you are, this might be the best book you've read.
3
Attention conservation notice: 3,000+ words of longform quotes by various folks on the nature of personal identity in a posthuman future, and hiveminds / clans
As an aside, one of the key themes running throughout the Quantum Thief trilogy is the question of how you might maintain personal identity (in the pragmatic security sense, not the philosophical one) in a future so posthuman that minds can be copied and forked indefinitely over time. To spoil Hannu's answer:
I take Anders Sandberg's answer to be on the other end of this spectrum; he doesn't mind changing over time such that he might end up wanting different things:
(I have mixed feelings about Anders' take: I have myself changed so profoundly since youth that that my younger self would not just disendorse but be horrified by the person I am now, yet I did endorse every step along the way, and current-me still does upon reflection (but of course I do). Would current-me also endorse a similar degree of change going forward, even subject to every step being endorsed by the me right before change? Most likely not, perhaps excepting changes towards some sort of reflective equilibrium.)
I interpret Holden Karnofsky's take to be somewhere in between, perhaps closer to Hannu's answer. Holden remarked that he doesn't find most paradoxical thought experiments about personal identity (e.g. "Would a duplicate of you be "you?"" or "If you got physically destroyed and replaced with an exact duplicate of yourself, did you die?") all that confounding because his personal philosophy on "what counts as death" dissolves them, and that his philosophy is simple, comprising just 2 aspects: constant replacement ("in an important sense, I stop existing and am replaced by a new person each moment") and kinship with future selves. Elaborating on the latter:
Richard Ngo goes in a different direction with the "personal identity in a posthuman future" question:
(I thought it was both interesting and predictable that Rob would f
1
The short story The Epiphany of Gliese 581 by Fernando Borretti has something of the same vibe as Rajaniemi's QT trilogy; Borretti describes it as inspired by Orion's Arm and the works of David Zindell. Here's a passage describing a flourishing star system already transformed by weakly posthuman tech:
Another star system, this time still being transformed:
I enjoyed these passages from Henrik Karlsson's essay Cultivating a state of mind where new ideas are born on the introspections of Alexander Grothendieck, arguably the deepest mathematical thinker of the 20th century.
...In June 1983, Alexander Grothendieck sits down to write the preface to a mathematical manuscript called Pursuing Stacks. He is concerned by what he sees as a tacit disdain for the more “feminine side” of mathematics (which is related to what I’m calling the solitary creative state) in favor of the “hammer and chisel” of the finished theo
3
A few days ago, I was thinking about matrices and determinants. I noticed that I know the formula for the determinant, but I still lack the feeling of what the determinant is. I played with that thought for some time, and then it occurred to me, that if you imagine the rows in the matrix as vectors in n-dimensional space, then the determinant of that matrix is the volume of the n-dimensional body whose edges are those vectors.
And suddenly it all made a fucking sense. The determinant is zero when the vectors are linearly dependent? Of course, that means that the n-dimensional body has been flattened into n-1 dimensions (or less), and therefore its volume is zero. The determinant doesn't change if you add a multiple of a row to some other row? Of course, that means moving the "top" of the n-dimensional body in a direction parallel to the "bottom", so that neither the bottom nor the height changes; of course the volume (defined as the area of the bottom multiplied by the height) stays the same. What about the determinant being negative? Oh, that just means whether the edges are "clockwise" or "counter-clockwise" in the n-dimensional space. It all makes perfect sense!
Then I checked Wikipedia... and yeah, it was already there. So much for my Nobel prize.
But it still felt fucking good. (And if I am not too lazy, one day I may write a blog article about it.)
Reinventing the wheel is not a waste of time. I will probably remember this forever, and the words "determinant of the matrix" will never feel the same. Who knows, maybe this will help me figure out something else later. And if I keep doing that, hypothetically speaking, some of those discoveries might even be original.
(The practical problem is that none of this can pay my bills.)
3
I kind of envy that you figured this out yourself — I learned the parallelipiped hypervolume interpretation of the determinant from browsing forums (probably this MSE question's responses). Also, please do write that blog article.
Yeah, I hope you will! I'm reminded of what Scott Aaronson said recently:
2
Hal Finney's reflections on the comprehensibility of posthumans, from the Vinge singularity discussion which took place on the Extropians email list back in the day:
1
Linking to a previous comment: 3,000+ words of longform quotes by various folks on the nature of personal identity in a posthuman future, and hiveminds / clans, using Hannu Rajaniemi's Quantum Thief trilogy as a jumping-off point.
Scott's The Colors Of Her Coat is the best writing I've read by him in a long while. Quoting this part in particular as a self-reminder and bulwark against the faux-sophisticated world-weariness I sometimes slip into:
...Chesterton’s answer to the semantic apocalypse is to will yourself out of it. If you can’t enjoy My Neighbor Totoro after seeing too many Ghiblified photos, that’s a skill issue. Keep watching sunsets until each one becomes as beautiful as the first...
If you insist that anything too common, anything come by too cheaply, must be bor
I find both the views below compellingly argued in the abstract, despite being diametrically opposed, and I wonder which one will turn out to be the case and how I could tell, or alternatively if I were betting on one view over another, how should I crystallise the bet(s).
One is exemplified by what Jason Crawford wrote here:
...The acceleration of material progress has always concerned critics who fear that we will fail to keep up with the pace of change. Alvin Toffler, in a 1965 essay that coined the term “future shock,” wrote:
I believe that most human beings
Some ongoing efforts to mechanize mathematical taste, described by Adam Marblestone in Automating Math:
...Yoshua Bengio, one of the “fathers” of deep learning, thinks we might be able to use information theory to capture something about what makes a mathematical conjecture “interesting.” Part of the idea is that such conjectures compress large amounts of information about the body of mathematical knowledge into a small number of short, compact statements. If AI could optimize for some notion of “explanatory power” (roughly, how vast a range of disparate knowl
How to quantify how much impact being smarter makes? This is too big a question and there are many more interesting ways to answer it than the following, but computer chess is interesting in this context because it lets you quantify compute vs win probability, which seems like one way to narrowly proxy the original question. Laskos did an interesting test in 2013 with Houdini 3 by playing a large number of games on 2x nodes vs 1x nodes per move level and computing p(win | "100% smarter"). The win probability gain above chance i.e. 50% drops from +35.1% in ...
3
The diminishing returns isn't too surprising, because you are holding the model size fixed (whatever that is for Houdini 3), and the search sigmoids hard. Hence, diminishing returns as you jump well past the initial few searches with the largest gains, to large search budgets like 2k vs 4k (and higher).
This is not necessarily related to 'approaching perfection', because you can see the sigmoid of the search budget even with weak models very far from the known oracle performance (as well as stronger models); for example, NNs playing Hex: https://arxiv.org/pdf/2104.03113#page=5 Since it's a sigmoid, at a certain point, your returns will steeply diminish and indeed start to look like a flat line and a mere 2x increase in search budget does little. This is why you cannot simply replace larger models with small models that you search the hell out of: because you hit that sigmoid where improvement basically stops happening.
At that point, you need a smarter model, which can make intrinsically better choices about where to explore, and isn't trapped dumping endless searches into its own blind spots & errors. (At least, that's how I think of it qualitatively: the sigmoiding happens because of 'unknown unknowns', where the model can't see a key error it made somewhere along the way, and so almost all searches increasingly explore dead branches that a better model would've discarded immediately in favor of the true branch. Maybe you can think of very large search budgets applied to a weak model as the weak model 'approaching perfection... of its errors'? In the spirit of the old Dijkstra quip, 'a mistake carried through to perfection'. Remember, no matter how deeply you search, your opponent still gets to choose his move, and you don't; and what you predict may not be what he will select.)
Fortunately, 'when making an axe handle with an axe, the model is indeed near at hand', and a weak model which has been 'policy-improved' by search is, for that one datapoint, equivalen
1
Thanks, I especially appreciate that NNs playing Hex paper; Figure 8 in particular amazes me in illustrating how much more quickly perf. vs test-time compute sigmoids than I anticipated even after reading your comment. I'm guessing https://www.gwern.net/ has papers with the analogue of Fig 8 for smarter models, in which case it's time to go rummaging around...
Just reread Scott Aaronson's We Are the God of the Gaps (a little poem) from 2022:
...When the machines outperform us on every goal for which performance can be quantified,
When the machines outpredict us on all events whose probabilities are meaningful,
When they not only prove better theorems and build better bridges, but write better Shakespeare than Shakespeare and better Beatles than the Beatles,
All that will be left to us is the ill-defined and unquantifiable,
The interstices of Knightian uncertainty in the world,
The utility functions that no one has yet wr
This remark at 16:10 by Dwarkesh Patel on his most recent podcast interview AMA: Career Advice Given AGI, How I Research ft. Sholto & Trenton was pretty funny:
(After Sarah Paine comes geneticist David Reich, then Satya Nadella and Mark Zuckerberg, "then [Sholto & Trenton] or Leopold (Aschenbrenner) or something, then you get to the lab CEOs or something")
This seems to underrate the value of distribution. I suspect another factor to take into account is the degree of audience overlap. Like there's a lot of value in booking a guest who has been on a bunch of podcasts, so long as your particular audience isn't likely to have been exposed to them.