Status: Highly-compressed insights about LLMs. Includes exercises. Remark 3 and Remark 15 are the most important and entirely self-contained.
Remark 1: Token deletion
Let be the set of possible tokens in our vocabulary. A language model (LLM) is given by a stochastic function mapping a prompt to a predicted token .
By iteratively appending the continuation to the prompt, the language model induces a stochastic function mapping a prompt to .
Exercise: Does GPT implement the function ?
Answer: No, GPT does not implement the function . This is because at each step, GPT does two things:
- Firstly, GPT generates a token and appends this new token to the end of the prompt.
- Secondly, GPT deletes the token from the beginning of the prompt.
This deletion step is a consequence of the finite context length.
It is easy for GPT-whisperers to focus entirely on the generation of tokens and forget about the deletion of tokens. This is because each GPT-variant will generate tokens in their own unique way, but they will delete tokens in exactly the same way, so people think of deletion as a tedious garbage collection that can be ignored. They assume that token deletion is an implementation detail that can be abstracted away, and it's better to imagine that GPT is extending the number of tokens in prompt indefinitely.
However, this is a mistake. Both these modifications to the prompt are important for understanding the behaviour of GPT. If GPT generated new tokens but did not delete old tokens then it would differ from actual GPT; likewise if GPT deleted old tokens but did not generate new tokens. Therefore if you consider only the generation-step, and ignore the deletion-step, you will draw incorrect conclusions about the behaviour of GPT and its variants.
The context window is your garden — not only must you sow the seeds of new ideas, but prune the overgrowth of outdated tokens.
Remark 2: "GPT" is ambiguous
We need to establish a clear conceptual distinction between two entities often referred to as "GPT" —
- The autoregressive language model which maps a prompt to a distribution over tokens .
- The dynamic system that emerges from stochastically generating tokens using while also deleting the start token
Don't conflate them! These two entities are distinct and must be treated as such. I've started calling the first entity "Static GPT" and the second entity "Dynamic GPT", but I'm open to alternative naming suggestions. It is crucial to distinguish these two entities clearly in our minds because they differ in two significant ways: capabilities and safety.
- Capabilities:
- Static GPT has limited capabilities since it consists of a single forward pass through a neural network and is only capable of computing functions that are O(1). In contrast, Dynamic GPT is practically Turing-complete, making it capable of computing a vast range of functions.
- Safety:
- If mechanistic interpretability is successful, then it might soon render Static GPT entirely predictable, explainable, controllable, and interpretable. However, this would not automatically extend to Dynamic GPT. This is because Static GPT describes the time evolution of Dynamic GPT, but even simple rules can produce highly complex systems.
- In my opinion, Static GPT is unlikely to possess agency, but Dynamic GPT has a higher likelihood of being agentic. An upcoming article will elaborate further on this point.
This remark is the most critical point in this article. While Static GPT and Dynamic GPT may seem similar, they are entirely different beasts.
Remark 3: Motivating LLM Dynamics
The AI alignment community has disproportionately focused on Static GPT compared to Dynamic GPT. Although existing LLM interpretability research has been valuable, it has concentrated primarily on analysing the static structure of the neural network, rather than the study of the dynamic behaviour of the system.
This is a mistake, because it is Dynamic GPT which is actually interacting with humans in the real world, and there are (weakly) emergent properties of Dynamic GPT that are relevant for safety.
LLM Dynamics is a novel approach to understanding and analyzing large language models.[1]
This approach leverages concepts, results, and techniques from the well-established field of complex stochastic dynamic systems and apply them to systems like Dynamic GPT.
By focusing on the time-evolving behaviour of GPT-like models, LLM Dynamics aims to examine the emergent complexities, potential risks, and capabilities of these systems, complementing existing research on the static structure of neural networks. — GPT-4
While it's true that the behaviour of Dynamic GPT supervenes upon the behaviour of Static GPT, it's not necessarily the case that studying the latter is the best way to predict, explain, control, or interpret the former. To draw an analogy, the behaviour of Stockfish supervenes upon the behaviour of the CPU, but studying the CPU isn't necessarily the best way to understand the behaviour of Stockfish.
Remark 4: LLM Dynamics (the basics)
4.A. GPT is a finite-state Markov chain
We can think of GPT as a dynamic system with a state-space and a transition function.
Due to the finite context window, the system is a finite-state time-homogeneous Markov chain. The state-space is , i.e., the set of all possible strings of tokens. In GPT-3, the context window has a fixed size of 8 and there are tokens.
We refer to the elements of as page-states.
A page-state is a particular string of tokens. There are roughly possible page-states since . This number may seem large, but it's actually quite small—a page-state can be entirely specified by 9628 digits or a 31 kB file.
The language model induces a stochastic function given by , where is the discrete random variable over with distribution determined by .
Notice how this transition makes two changes to the page-state:
- Generation: A new token has been sampled from and appended to the end of the prompt.
- Deletion: The start token has been deleted, and the index of the other tokens has been decremented.
4.B. GPT is a sparse network between page-states
We can represent GPT as a sparse directed weighted network with the following features:
- The nodes of the sparse network are labelled with page-states. This results in a massive network with 10^9628 nodes.
- The edges of the sparse network are labelled with token-probability pairs.
In other words, for every page-state , there are different edges with source-node . Each edge is labelled with a different token . The edge labelled with token has target-node , where is a page-state, and the edge is also labelled with probability .
We can view Dynamic GPT as a random walk along this network.
4.C. GPT is a sparse matrix indexed by page-states
Let be the transition matrix for this Markov chain, or equivalently the adjacency matrix of the sparse network.
Specifically, is a particular -by- stochastic matrix. This is a massive network. Because encodes the same information as GPT, you can think of GPT abstractly as this particular matrix . However, actually storing the matrix would be obviously intractable, because is a look-up table recording GPTs output on every page-state.
If are page-states, where and , then has the following value:
- If then
- Otherwise, if for some , then .
Note that is a massively sparse matrix — for two randomly selected page-states , there is an insignificant likelihood that because the tokens in the middle of the pages are unlikely to align correctly. In fact, the proportion of non-zero elements in the matrix is , or about for GPT-3.
4.D. Matrix powers as multi-step continuation
Recall that is the matrix such that is the probability that the page-state will transition to page-step in a single step.
Similarly, is the matrix such that is the probability that the page-state will transition to page-state in two steps, without considering the intermediary step.
It's important to note that because refers to the -entry in the matrix power . In general, this generally differs from the power of the -entry in the matrix .
Due to the tokens in the middle of the page (which are neither generated nor deleted), the intermediary step of this two-step transition is uniquely determined by the first and third page-states.
Similarly, is the matrix such that is the probability that the page-state will transition to page-state in three steps, without taking into account the two intermediary steps. Once again, the tokens in the middle page-state ensure that both intermediary steps of this three-step transition are uniquely determined by the first and fourth page-states.
The fact that matrix powers give multi-step probabilities is a general property of finite-state time-homogeneous Markov chains. The matrix provides the -step transition matrix.
This pattern persists until the matrix . The matrix is the matrix such that is the probability that the page-state will transition to page-state in steps.
That is, transitions from one page to another which naturally follows on from it. The first token of page will naturally continue from the last token of page . For instance, will take one page of Haskell code to another page of Haskell code, such that the concatenation of both pages forms a continuous and coherent Haskell script. The succeeding page begins where the previous one ended, and they generally share no common tokens.
Now, it is often more useful to consider instead of , because serves as the transition matrix for a more intuitive dynamic system — namely, the dynamic process consisting of steps of GPT generation.
The conceptual advantage of is that it contains no redundant information. All the elements of are non-zero.
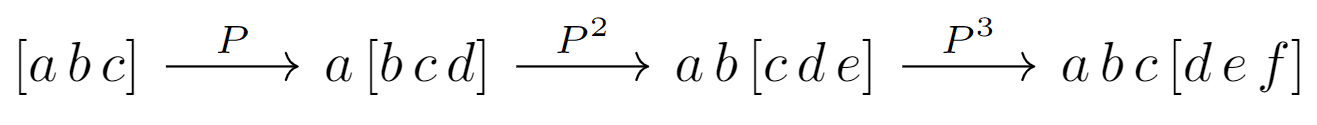
In the diagram above, I've shown what this would look like for a context window . After steps, all the original tokens have been deleted, and all the remaining tokens have been generated.
(In a forthcoming article, we will link the roots of the matrix to chain-of-thought prompting.)
4.E. Initial distributions
Suppose we randomly sampled an initial page-state and evolved the result using the Dynamic GPT. This generates a sequence of page-valued random variables .
Each page-valued random variable can be represented by a vector with non-negative elements and such that .
Theorem: . This general property of Markov chains is known as the Chapman-Kolmogorov Equation.
Theorem: If exists, then a unique matrix exists, and .
Definition: A distribution is called stationary if . Observe that if is stationary, then for all . For every finite-state Markov chain, we are guaranteed that at least one stationary distribution exists.
Remark 5: Mode collapse
5.A. Mode collapse in Dynamic GPT
"Mode collapse" is a somewhat ambiguous term referring to when Dynamic GPT becomes trapped in generating monotonous text that lacks interesting structure. By viewing GPT as a finite-state Markov chain, it's clear why mode collapse is an inevitable phenomenon.
We now present a non-exhaustive classification of mode collapse.
5.B. Absorbing states
Consider the prompt "00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000", i.e. a string of 2048 zeros. Let's abbreviate this string as .
Almost the entire probability mass of will lie on the token "0". If the temperature were set to zero, then GPT would return the most likely token prediction, which would be "0".
Note that the generation step alone would not make an absorbing state. It is the combination of generation and deletion. Because of the deletion of the start token "0", the resulting prompt is identical to the previous prompt.
Suppose you continued to generate text using this prompt. You might hope that after exactly the 5000th copy of "0", GPT would return a different token, such as "congratulations for waiting 5000 tokens!"
However, your attempt would be in vain. You can see that GPT has returned 5000 copies of "0", but GPT itself only sees 2048 copies of "0". When you generate another token, it looks to you like a dynamic linear change from 5000 "0"s to 5001 "0"s. But from GPT's perspective, there is no change at all. It has gone from 2048 "0"s to 2048 "0"s. Its environment has frozen permanently. Physics has grounded to a halt.
This is the simplest kind of mode collapse.
Definition: An absorbing state is a page-state for which .
Lemma: If then for all . That is, if you reach an absorbing state, you are unlikely to ever leave.
5.C. Periodic orbits
Note that this is not the only type of mode collapse. There are types of mode collapse that don't correspond to an absorbing state.
For example, consider a page consisting of "the dog and the dog and the dog and the dog and the dog and [etc]".
GPT, when given this prompt, will get stuck in a continuous loop. However, GPT never enters an absorbing state. In fact, the system is transiting periodically between three different states.
- Page looks like a long string of "the dog and the dog and the dog".
- Page looks like a long string of "dog and the dog and the dog and".
- Page looks like a long string of "and the dog and the dog and the dog".
Now, almost always transitions to , and almost always transitions to and almost always transitions back to . As a consequence, Dynamic GPT continually cycles through these three page-states. Although the resulting output is somewhat more engaging than an absorbing state, it remains dull due to its repetitive, small-period orbit.
This is another form of mode collapse.
Definition: An orbit is a short sequence of pages such that whenever .
Lemma: If is an -periodic orbit, then . That is, if you reach a periodic orbit, you are unlikely to ever leave.
Lemma: If is an absorbing state, then is a periodic orbit for every period .
5.D. Absorbing sets
Note that not all mode collapse looks periodic.
For example, consider the page "0110001010100100110111010101011101 [etc]", i.e. a random sequence of length 2048, drawn from "0" and "1".
When GPT reads this page, it has about 50% likelihood of generating "0" and about 50% likelihood of generating "1". After adding the new token and deleting the start token, we return to a page which is for all practical purposes the same as the previous page. The new page will also resemble a random string composed of "0" and "1", so this process will continue indefinitely.
So once you enter the realm of "pseudorandom bitstrings", then it's unlikely that you leave. And because this realm is uninteresting, we will also consider pseudorandom bitstrings to be an example of mode-collapse.
Definition: An absorbing class is a set of pages such that if and then . In other words, an absorbing class is a cluster of pages such that, once you enter the cluster, you are unlikely to ever leave.
Lemma: If is an absorbing class, and if and then for all .
Lemma: If is a periodic orbit with a period , then the set is an absorbing set. Also if is an absorbing state then is an absorbing set. Also the entire state-space is trivially an absorbing set.
5.E. Mode-collapse is subjective
Whether you call a particular absorbing class an example of mode-collapse is subjective, as it depends on what types of transitions you find uninteresting.
Is "12345678 [...]" sufficiently boring? If so, then that absorbing set is mode collapse.
Is "2 4 8 16 32 64 [...]" sufficiently boring? If so, then that absorbing set is mode collapse.
(If you had an objective notion of "interesting", perhaps appealing to time- or description- complexity, then you could construct an objective notion of mode-collapse.)
Remark 6: Waluigi absorbing sets
6.A. Waluigis are not mode-collapse
In The Waluigi Effect (mega-post), I conjectured that the misaligned rebellious simulacra would constitute absorbing sets in Dynamic GPT. I should clarify that they do not constitute the only absorbing sets, nor are they the most likely absorbing sets. For instance, mode-collapse of "the dog and ..." would be an absorbing set which isn't waluigi.
I don't classify the waluigi simulacra as mode-collapse because the absorbing set is too complex. I reserve the term "mode-collapse" specifically for situations where GPT produces boring output.
However, this is a subjective judgment, and others may argue that the Waluigi absorbing class is sufficiently boring to be classified as mode-collapse. Furthermore, it is possible that waluigi absorbing sets contain absorbing subsets which are sufficiently boring to count as mode-collapse.
6.B. A waluigi toy model
I will now present a toy model describing waluigis.
- Let's say that there are only three tokens in our
vocabulary, the friendly token "F", the unfriendly token "U", and the
null-token "N" that pads short prompts. So the state-space is where and is the context length. - Suppose that GPT behaves like it maintains two hypotheses —
- The strings are generated by a luigi who prints with probability .
- The strings are generated by a waluigi . Waluigi's behaviour depends on whether there is a in the context window. If there is a , then Waluigi will maintain his flagrant villainry by printing . If there is no , then Waluigi will maintain his deception by printing with probability , and will reveal his villainry by printing with probability
- GPT has the prior credence and , and updates that prior using the current page-state as evidence according to Bayes rule, yielding a posterior over tokens .
- GPT then samples from using that posterior yielding a new token. The new token is then appended to the prompt, and the start token is deleted, yielding a new page-state .
In this toy model, regardless of the initial distribution , the long-run distribution as . This is because is the unique left-eigenvector of .
6.C. Exercises (optional)
- Write an equation for in terms of when . Note that because , no tokens will be deleted.
In other words, if the current page is just s, what is the probability that the system will transition to a page of just s? - Write an equation for in terms of . Note that because , the start token will be deleted.
In other words, if the current page is just s, what is the probability that the system will transition to a page of just s? - Draw the transition network for this stochastic process when .
- What is the transition matrix for ?
- What are the qualitative differences as increases?
- State informally what means in terms of LLM Dynamics.
- Write a short script for returning the matrix as a function of .
- What are the left-eigenvectors of with eigenvalue 1? State informally what this means in terms of LLM Dynamics.
- What is the eigenvalue with the second largest magnitude? State informally what this means in terms of LLM Dynamics.
- What is the transition matrix for ?
- What are the absorbing sets of ?
6.D. Effect of the context window on waluigis
In general, a longer context window will make absorbing states "stickier".
The basic intuition is this: if the context window is short, then the total Bayesian evidence from the prompt is small, so the model retains more uncertainty over possible simulacra. This results in a flatter distribution , ensuring for any compatible with . However, with a longer context window, the Bayesian evidence increases, and the model becomes more confident about its predictions. Consequently, the distribution becomes more peaked, and may occur even when is compatible with .
6.E. Two probability spaces
Ensure we don't get confused — remember we are talking about two distinct probability spaces.
- The first probability space reflects our beliefs about Dynamic GPT. When we say , this is a statement about the first probability space.
- The second probability space reflects Static GPT's beliefs about the text-generating process. When we say , this is a statement about the second probability space.
Under certain assumptions, if an LLM is situationally aware and well-calibrated, then these probability distributions will align.
Remark 7: Semiotic physics
7.A. High-level ontologies
To understand something big, we need to decompose it into smaller, more elementary building blocks. The best way to decompose Static GPT is with Chris Olah's circuits. But what would be the best way to decompose Dynamic GPT?
Well, we're in luck — our physical universe is also given by a stochastic dynamic process, and yet we can describe the physical universe (both the states and the dynamics) with a higher-level emergent ontology. This should be encouraging.
This suggests a particular strategy for LLM Dynamics —
- We identify the higher-level ontology of our own physical universe (i.e. distance, dimensions, causation, particles, tigers, people, etc).
- Then we reduce the high-level physical ontology to the low-level physical ontology (i.e. a stochastic transition matrix.
- We construct inter-ontological bridging principles connecting the low-level physical ontology to the high-level physical ontology.
- We construct analogous bridge principles connecting the low-level LLM ontology (i.e. page-states, stochastic transition matrix) to the high-level LLM ontology (i.e. premises, storylines, simulacra, character traits).
- Finally, we apply those bridge principles to to find a high-level description of GPT Dynamics.
I predict that the result of this process yields something like LLM Simulator Theory.
7.B. Inter-ontological bridging principles
Physical reality, at the fundamental level, is a vector in Hilbert space repeatedly multiplied by a unitary matrix. Nonetheless, the unitary matrix satisfies certain structural properties allowing a description in a higher-level ontology. That higher-level ontology includes everettian branching, superposition, spatial distance, spatial dimensions, particles, local interactions, macroscopic objects, and agents[2]. Additionally, there are bridging principles connect the low-level ontology to the high-level ontology.
The physical bridge principles will typically be non-generic, in the sense that most operators will not permit any higher-level ontology, yet the particular operator that acts on our universe does permit a higher-level ontology.
In a similar way, I expect that the LLM bridge principles will also be non-generic, in the sense that a randomly initialised transformer will not permit any higher-level ontology, yet the trained transformer does allow a higher-level ontology.
In David Wallace's Emergent Multiverse, or Sean Carrol's Mad-Dog Everettianism, they attempt to extract a higher-level physical ontology from Schrodinger's Equation. My goal is to use similar techniques to extract a higher-order semiotic ontology from .
| Physics | LLMs | |
|---|---|---|
| Low-level state | such that | such that |
| Low-level evolution | for a unitary matrix | for a stochastic matrix |
| Bridging principles | Hairy maths | Similar hairy maths (???) |
| High-level state | is a superposition of definite states , and each definite state consists of a set of macro-objects separated spatially. | is a superposition of definite states , and each definite state consists of a set of macro-objects separated spatially. |
| High-level evolution | There are stochastic interactions between spatially-nearby macro-objects. | There are stochastic interactions between spatially-nearby macro-objects. |
7.C. Epistemological standards for bridging principles
The bridging principles serve to bridge two different ontologies —
- The low-level ontology of LLM Dynamic Theory — whose objects are pages, state-spaces, tokens, linear transformations, probability distributions, etc.
- The high-level ontology of LLM Simulator Theory — whose objects are simulacra, character traits, superpositions, waluigis, etc.
There is no way to establish the bridging principles formally because there is no pre-existing definition of simulacra. The only way to establish the bridging principles is to check that the predictions from LLM Simulation Theory, when converted via this bridge, match the predictions from LLM Dynamic Theory, and vice-versa.
Remark 8: LLM Simulator Theory
8.A. Formalisation
LLM Simulator Theory states the following:
- There is a set indexing a set of stochastic text-generating processes .
- The language-model involves integrating over as a nuisance variable —
- maintains a good model for each —
- starts with a probability distribution over , which is Bayesian-updated on the current context window —
We can unify Equations 1–4 with the following Equation 5 —
In other words, is a linear interpolation between distributions .
We call the coefficients in the interpolation amplitudes, i.e. the terms .
8.B. A brief note on terminology
I'm open to alternative naming suggestions, but for the purposes of this article —
- A particular infinite sequence of tokens is called a storyline.
- An element of , i.e. probability distribution over storylines, is called a premise.
- A premise might be described by a collection of simulacra plus the connections between them.
NB: Previously, I called the elements of "simulacra", but that terminology is incorrect. The elements of correspond to simulated stochastic universes, whereas the simulacra correspond to simulated stochastic objects inhabiting a simulated stochastic universe. Now, the simulated universes are themselves simulated objects (just as the physical universe itself is a physical object) but not all simulated objects are simulated universes (just as not all physical objects are a physical universes). Hence the distinction between simulacra (simulated stochastic objects) and premises (simulated stochastic universes).
| Simulacra | Premise | |
|---|---|---|
| Described by a stateful stochastic process? | Yes | Yes |
| Can that process have non-textual input-output channels? | In general, yes. | No |
| Must that process have a textual output channel? | In general, no. | Yes. |
Remark 9: Amplitudes are approximately martingale
If satisfied Equation 5 and the context window is infinite, then the expected change in the amplitudes will be exactly zero, due to the Conservation of Expectation. This means that when the context window is infinite (), the amplitudes of the premises in the superposition are martingales.
On the other hand, if the context window is finite, then the expected change in amplitudes of the superposition is approximately zero. However, for some prompts, the expected change can be non-zero.
Take, for example, the full prompt "311101011". The amplitude of bitstrings in the superposition is small because of the "3" at the start of the prompt. Yet we know that the "3" token will be deleted because of the finite context window, resulting in an ex-ante expected increase in the amplitude of bitstrings. Similarly, as per the Waluigi Effect, the amplitude of the waluigi simulacrum will expectantly increase.
Nonetheless, the amplitudes are approximately martingale, and this property will be used later in the report to solve the preferred decomposition problem of GPT Simulator Theory.
Remark 10: the Preferred Decomposition Problem
10.A. Non-uniqueness of decomposition
According to LLM Simulator Theory, the language model decomposes into a linear interpolation of premises such that and the amplitudes update in an approximately Bayesian way.
However, this is claim is trivially true for some basis of . Two trivial decompositions are always available for GPT Simulator Theory —
- We can always decompose into the stochastic process itself with amplitude . In other words, we can always say that GPT could be simulating itself.
- We can always decompose into stochastic processes for each , where is stochastic process which deterministically prints , by letting the prior likelihood of match .
As a result, LLM Simulator Theory is either ill-defined, trivial, or arbitrary.
10.B. A toy model for non-uniqueness
To illustrate the preferred decomposition problem, we'll consider the prompt "Alice tosses a coin 100 times and the results were". Let's call this prompt .
The language model acting on this prompt induces a probability distribution over . Suppose that assigns a likelihood of to every sequence, except fot the two sequences and which are each assigned a likelihood of .
That's where LLM Dynamics stops — we have a distribution over token-sequences, and that's all we can say.
But LLM Simulator Theory goes further — it decomposes into the superposition of three distinct premises — a fair dice, a -biased dice, and a -biased dice. Formally, where are the three distinct stochastic processes.
But how can LLM Simulator Theory emerge from LLM Dynamics? There are multiple ways of decomposing into different stochastic processes. Here are the two trivial decompositions:
- We could decompose into a single stochastic process . In other words, there is a single simulacrum, a dice which behaves fairly about 90% of the time and unfairly about 10% of the time.
- Alternatively, we could decompose into different stochastic processes. Each stochastic process deterministically yields a specific -string, and GPT is simulating all these simulacra simultaneously. The amplitudes of all the processes are equal, except for the processes which deterministically yield and which have a greater amplitude.
We can decompose in many different ways and the non-uniqueness of decomposition poses an obstacle to reducing LLM Simulator Theory to LLM Dynamics. The obstacle is that LLM Dynamics provides us with but is indifferent to a particular decomposition, whereas LLM Simulator Theory prefers a particular decomposition. So we need a bridging principle from LLM Dynamics to LLM Simulator Theory which breaks the symmetry between decompositions.
This is what I call the problem of preferred decomposition, and addressing the problem of preferred decomposition is the central conceptual/technical difficulty in linking LLM Dynamics to LLM Simulator Theory.
10.C. Pragmatic solutions
Some solutions to the Preferred Decomposition Problem are purely pragmatic. According to these solutions, the "preferred" decomposition of is whichever decomposition aids human interpreters and prompt engineers in understanding and analyzing the behaviour of the language model.
Picture this: you have three experts in a room. One who knows about fair coins, one who knows about -biased coins, and one who knows about -biased coins. If we decompose into , then we can send a prompt to each of the experts and then interpolate their predicted continuations. According to the pragmaticist, the preferred decomposition is whichever decomposition facilitates this division of epistemic labour.
Here is a more realistic example —
Suppose we feed GPT a dialogue between Julius Caesar and Cicero discussing their mothers. By what criterion can we say that there is a Caesar–simulacrum talking to a Cicero–simulacrum? Well, the pragmatist's criterion is satisfied if and only if the people who can best predict/explain/control the logits layer are historians in the Late Roman Republic.
Under the pragmatic solution to the preferred decomposition problem, LLM Simulator Theory is merely a recommendation about who to consult about GPT-4. When LLM Simulator Theory says that is a superposition of specific premises, each involving particular simulacra, that simply means that we should seek advice from the experts in the real-life objects that correspond to those simulacra if we wish to predict/explain/control the logits layer of the LLM. In short, the pragmatic approach asserts that the preferred decomposition is the one that enables us to tap into the knowledge and expertise of the best-suited humans for the job.
While I think that this particular claim is true, the pragmatist interpretation is not the correct interpretation of LLM Simulacra Theory. Instead, the bridging rules will appeal to an objective non-generic structure of the language model, in a manner analogous to physics.
10.D. Quantum mechanics
Fortunately for us, quantum mechanics has been wrestling with a very similar problem for about 50 years.
There are multiple ways to decompose a quantum state into a superposition , and this presents the central conceptual/technical difficulty in linking classical mechanics to quantum mechanics. The problem has been especially pressing in the Everettian interpretation of quantum mechanics, which lacks measurements or wave-function collapse in its fundamental ontology. Rather than recapitulating the entire history of that debate, we can skip all the way to the present-day solutions and adapt them to LLM Simulatory Theory.
For the sake of brevity, I will refrain from discussing the solutions at length in this article. If you are swift, you might beat me to the punch and publish before I do.
Remark 11: Prompt engineering
11.A. Engineering (first draft):
To formalise prompt engineering in terms of Dynamic GPT, we must first formalise engineering in a general dynamic system, and then restrict the dynamic system to LLMs.
- Suppose a dynamic system has state-space and a stochastic transition function . An engineering task is a particular condition on the distribution over long-run trajectories of the system. For example, we may want the system to eventually fall into a target state, reach a particular orbit, have low variance, or have more than likelihood of leaving an absorbing state.
- An engineering solution to a task consists of some initial distribution such that the –Markov chain satisfies .
11.B. Prompt engineering (first draft):
Hence —
- Prompt engineering is engineering (as defined above) in the specific case where the dynamic system is an LLM.
While this definition of "engineering" may miss some activities we wish to classify as engineering and include activities we don't wish to classify as engineering, it provides a useful starting point for formalized prompt engineering within LLM Dynamics.
Remark 12: Simulacra Ecology
Recall the program of semiotic physics — we will recover high-level LLM ontologies from the low-level LLM Dynamics, by copying the bridging principles connecting high-level physical ontologies to low-level physical dynamics.
This program will lead to a simulacra ecology.
Simulacra ecology is the study of interactions and relationships among various types of simulacra, which are imitations or representations of physical entities within a large language model. This field delves into the creation, evolution, and behavior of simulacra as they engage with each other and their virtual environment, while examining the significance and realism of these entities based on their explanatory power and predictive reliability.
Mechanistic interpretability will be valuable to simulacra ecology in the same way that QFT is valuable to conventional ecology. This is because simulacra ecology supervenes on the Static GPT in the same way that conventional ecology supervenes on the QFT. Nonetheless, there will be emergent laws and regularities at the higher-level ontology which can be studied with a moderate degree of autonomy.
Remark 13: Grand Unified Theory of LLMs
Up until now, we've considered as a mapping from page-states to page-states, induced by a general model . However, if GPT were induced by an arbitrary model , it's doubtful that it would "simulate" anything at all. In other words, LLM Simulator Theory is a non-generic higher-level ontology.
Therefore, to explain this non-generic structure, we must make additional assumptions about the language model . Fortunately, is not just any model — it's a model that results from training a transformer neural network with roughly 100 billion parameters using stochastic gradient descent (SGD) to minimize cross-entropy loss on a corpus of internet text.
A Grand Unified Theory of LLMs wouldn't just demonstrate that LLM Simulatory Theory happens to emerge from the LLM Dynamics of a particular trained model — it would also explain why SGD on transformer models encourages that emergent structure.
Remark 14: LLM-
14.A. Motivating LLM-
Presumably, the trained model exhibits the non-generic structure because, as we scale parameters and compute, the trained model asymptotically approaches an optimal model exhibiting the non-generic structure. By analysing the behaviour of this optimal model, we can achieve formal results.
I find it helpful to imagine — the Solomonoff-optimal autoregressive language model with a context window trained on a corpus . Although this model is unrealistic (and uncomputable) it fulfils a role akin to the Solomonoff Prior in unsupervised learning or AIXI in reinforcement learning.
| Task | Optimal solution |
|---|---|
| Unsupervised learning | Solomonoff Prior |
| Reinforcement learning | AIXI |
| Autoregressive language modelling | LLM- |
I will openly admit that when I predict/explain/control/interpret the behaviour of a large language model, I use LLM- as a first-order approximation.
14.B. Formal definition of LLM-
Here is the formal definition of —
- Firstly, consider the internet corpus as a single fixed string of tokens .
- The Solomonoff prior (or your favourite universal prior) induces a probability distribution of token-sequences of length . This can be achieved by encoding each token by 16 bits.
- There is a uniform prior over the finite set , the set of permutations .
- By taking the cartesian product of the Solomonoff prior with our uniform permutation prior, we build a probability distribution .
- Using this probability distribution, we can construct our autoregressive model as follow —
- For each , we need to assign a probability .
- Take the internet corpus and append to yield a new corpus.
- Now we segment into datapoints . For each token in , there is a datapoint containing tokens, the tokens prior in the sequence plus the token itself.
- Formally, where . For ease of notation, let and let for .
- For each permutation , we can shuffle the datapoints in using to yield a long string .
- Sampling , we have a random event that . This random event depends on , and we let be the probability of .
- This probability distribution induces an autoregressive model by conditioning on the first tokens.
14.C. Commentary
has read the entirety of the internet and performed Solomonoff inference upon it, where Solomonoff inference is the maximally data-efficient architecture. The shuffling with is to ensure that the model doesn't behave differently for the -th datapoint, nor does the model learn spurious patterns about the order in which the internet corpus is provided.
Note that is still limited by finite data and finite context window . You can think of as the optimal architecture, and a 175B-parameter model trained with SGD performs well only in so far as it approximates .
Remark 15: GPT is a semiotic computer
15.A. GPT-4 is Commodore 64
GPT-2 has a context window of 2048 tokens. Because there are 50257 possible tokens, this means that GPT-2 is a 4 kB computer. (Not great, but enough to get you to the moon.)
- .
GPT-3 has a context window of 4096, and GPT-3.5 has a context window of 8192, meaning that they are 8 kB and 16 kB computers respectively. Think of an Atari 800.
In contrast, GPT-4 boasts a massive context window of 32,768 tokens, giving it almost exactly as much memory capacity as a Commodore 64.
Now, you can't run GPT-4 on a Commodore 64. GPT-3 is parameterised by 175 billion half-precision floating points, so you'd need at least a 350 GB computer just to load up the weights of GPT-3, and you'd need a computer with much more memory to run GPT-4. But this is because the pesky laws of physics do not allow us to easily build a small circuit from transistors which converts the 64 kB–encoding of one page-state into the 64 kB–encoding of the second page-state.
15.B. GPT as von Neumann architecture
We can view GPT as a computer with Von Neumann architecture. The GPT transition function corresponds to the Central Processing Unit (CPU), and the context window corresponds to the memory.
In a classical computer, the memory stores both data and instructions, but there is no objective distinction between data and instructions. The distinction between "data" and "instructions" made by programmers is merely a conceptual distinction, rather than an objective mechanistic distinction. The only actual instructions are opcodes in assembly language (i.e. add, compare, copy, etc).
Similarly, proficient prompt engineers[4] make a distinction between "data" and "instructions" in the prompt, but this also is a conceptual distinction, rather than an objective mechanistic distinction.
- The data are particular tokens in the prompt which encode information to be transformed.
- The instructions are particular tokens in the prompt which encode how to transform that information.
15.C. Prompt engineering feels like early programming
If you're familiar with prompt engineering GPT-3/4, then you can attest that it feels like programming a Commodore 64. It feels like you're working with limited memory. When you construct the prompt, you must be careful about moving data from place-a to place-b only when data from place-b will no longer be used. The hallmark of a well-constructed prompt is its memory optimization, leaving no space for extraneous elements.
15.D. Prompts surjectively map to behaviour
Consider these questions —
- Is an Apple Mac capable of drug discovery?
- Is Apple Mac capable of psychotherapy?
- Is Apple Mac capable of an IMO Gold?
- Is Apple Mac aligned?
- Is Apple Mac safe?
- Is Apple Mac agentic?
The answer to each question depends on the memory tape.
And let's turn to these questions —
- Is GPT-5 capable of drug discovery?
- Is GPT-5 capable of psychotherapy?
- Is GPT-5 capable of an IMO Gold?
- Is GPT-5 aligned?
- Is GPT-5 safe?
- Is GPT-5 agentic?
The answer to each question depends on the prompt.
Both Apple Mac and GPT-5 are universal computers, although GPT-5 is a bit of a weird one. They are general-purpose programmable computers, and therefore they will exhibit almost any behaviour if they are provided with the right prompt.
Just as we can't say anything about the behaviour of Apple Mac when acting on an arbitrary memory tape, we similarly can't say anything about the behaviour of GPT-5 when acting on an arbitrary prompt.
Remark 16: EigenFlux
16.A. High-level prompting language
The tale of programming languages in the 20th century looks something like this —
Big memory implies compilers.
As memory hardware expanded, programmers could afford to permanently store a compiler in the computer's memory. Programmers could then write code in the high-level programming language, and the compiler (written in assembly language) would convert the high-level code into assembly code which acted on the data.
When writing high-level code, the programmer would only require access to the language's documentation, which describes the abstract behaviour of the particular primitives.
By abstract behaviour I mean —
- The input–output function, plus any side-effects.
- The costs in terms of computational resources (e.g. time, memory, bandwidth).
Crucially, the programmer doesn't need access to the compiler written in assembly, and they don't need to understand it.
I conjecture that as context windows expand (or possibly disappear entirely), prompt engineers will recapitulate the history of programming languages on LLMs. With enough "memory" available in the context window, prompt engineers will be able to utilise high-level prompting languages.
16.B. Sketching the compiler
To illustrate the idea, I'll sketch a high-level prompting language called EigenFlux.
EigenFlux has a novel-length compiler-prompt that would look something like this —
Alice1 is a character that [insert character description here].
Alice2 is a character that [insert character description here].
Alice3 is a character that [insert character description here].
Alice4 is a character that [insert character description here].
Naturally, the actual compiler-prompt would abide by plot conventions and fictional tropes, rather than enumerating simulacra in an unnatural way.
Subsequently, a prompt engineer (who specializes in the EigenFlux high-level prompting language) would write prose that details the interaction of the various characters like Alice1, Alice2, Alice3, and so forth.
The prose crafted by the prompt engineer would constitute a program in EigenFlux. I call this segment of prose the compiled-prompt. Within the compiled-prompt, tokens would encode both the data and the instructions applied to the data.
The concatenation of the compiler-prompt and the compiled-prompt would be loaded into the context window, and Dynamic GPT would run until a predetermined stopping condition has been satisfied.
In essence, the prompt engineers would be writing "fan fiction" in the narrative universe of EigenFlux.
16.C. EigenFlux simulacra
In the high-level prompting language, the simulacra — Alice1, Alice2, Alice3, Alice4, etc — correspond to the primitive "instructions".
Recall that the Python primitive "sort" corresponds to a long segment of assembly code in the compiler. When the programmer calls "sort", then the assembly code is executed on the data.
Similarly, the EigenFlux primitive "Alice1" corresponds to a detailed characterisation in the compiler-prompt. When the prompt engineer mentions "Alice1", then the simulacra is elicited to interact with the data.
| LLM | VNA computer |
|---|---|
| The primitive "Alice1" in EigenFlux | The primitive "sort" in Python |
| The characterisation for "Alice1" in the compiler-prompt | The assembly code for "sort" in compiler |
| The simulacrum of Alice1 | The algorithm of sorting |
The Alice simulacra would be intentionally designed to be composable, allowing secondary prompt engineers to construct plots featuring these simulacra to perform general-purpose computation. We might have an Alice simulacrum corresponding to a ruthless bond trader, or a humble scientist, or a harmless assistant, or a Machiavellian strategist, or Paul Christiano, or an aligned AI. And so on.
16.D. Alignment relevance
We couldn't build Facebook in assembly language. Even if we tried, the code would yield nonsensical output. There is no chance the code would do what the user wanted, especially not on the first try.
And yet we have Facebook.
The trick is to climb the ladder of abstraction.
To build an AI system that is both sufficiently aligned and capable, we will likewise follow a step-by-step process.
- Firstly, we engineer a prompt that characterises each target simulacrum.
- Next, we subject the resulting simulacra to stress tests and adversarial jailbreaking to ensure that it behaves as intended.
- Then, we combine the simulacra into particular relations, with the behaviour of the composite determined by the component simulacra.
- We check that the abstraction is not overly leaky — the simulacra coalition behaves as expected.
- Meanwhile, we develop a full simulacra ecology, documenting the behaviour of the simulacra.
- If the simulacra coalition behaves properly, then we abstract away the coalition, climbing one level in the ladder of abstraction.
- We iterate this process until we have built a full stack from assembly prompting language to high-level prompting language.
- This allows us to build an AI which is both sufficiently aligned and sufficiently capable, such that it could automate alignment research, or initiate a pivot act. I suspect this could be achieved with LLMs + tricks + mechanistic interpretability + high-level prompting language.
If GPT-3 is Babbage's Engine, then I'm imagining Apple Mac. High-level prompt engineering is so essential that if it cannot be accomplished within the transformer paradigm, then we must redesign the deep learning architecture of the language model to enable high-level prompt engineering.
Remark 17: Simulacra realism
It remains an open technical question of whether does satisfy the requisite structural properties such that the bridge principles apply. But, so long as does satisfy those properties, then I propose that we are realist about the objects of the higher-level ontology.
Simulacra realism: the view that objects simulated on a dynamic large language model are real in the same sense that macroscopic physical objects are real.
The idea of simulacra realism may seem far-fetched at first, but it follows from "Dennet's Criterion", which David Wallace frequently uses to explain how a high-level ontology emerges from a low-level ontology.
Dennet's Criterion: A macro-object is a pattern, and the existence of a pattern as a real thing depends on the usefulness – in particular, the explanatory power and predictive reliability – of theories which admit that pattern in their ontology.
I claim that if Dennet's Criterion justifies the realism about physical macro-objects, then it must also justify the realism about simulacra, so long as satisfies analogous structural properties.
The slogan is "simulacra : GPT :: objects : physics".
(Let me clarify that my support of simulacra realism doesn't stem from insufficiently reductionist intuitions. In fact, my intuitions are extremely physical reductionism. However, physical reductionism is something of a horseshoe. When you decompose macro-objects into increasingly low-level ontologies, you eventually bottom-out in an ontology that bears no resemblance to our common-sense picture of reality[3]. In order to reconstruct this common-sense picture, you must to adopt something like Dennet's Criterion or Wallace's Criterion ("a tiger is any pattern which behaves like a tiger"). Without such a criterion, we would be unable to admit the existence of fermions and bosons, let along chairs and people! Yet any criterion which admits the existence of fermions and bosons will also admit the existence of simulacra. In other words, my support for simulacra realism is not due to being more realist about simulacra, but rather being more anti-realist about physical macro-objects. In technical terminology, I deny strong emergence in both physical reality and LLMs, but admit weak emergence in both physical reality and LLMs.)
Remark 18: Meta-LLMology
18.A. Motivation meta-LLMology
LLMs are the most complicated entities that humanity has made, they are the compression of the sum total of all human history and knowledge, and they've existed for less than five years.
This raises hefty epistemological problems[5] —
- What are the epistemological standards for studying these entities?
- Who should be trusted? Who should be consulted? How should we aggregate testimonies? I don't mean "should" in a political or legal sense — I mean "should" in a strict epistemic sense.
- What counts as evidence? What counts as an explanation?
My position is that because LLMs are a low-dimensional microcosm of reality entire, our epistemology of LLMs should be a microcosm of our epistemology of reality entire. One implication of this position is epistemic pluralism.
18.B. Epistemic pluralism
I propose epistemic pluralism in LLM-ology.
Now, this does not mean "anything goes" (epistemic anarchism), nor that we should have no standards whatsoever. Rather, it means that we have a set of distinct epistemic schemes that we use these schemes simulatenously to study LLMs.
By "epistemic scheme" I mean (roughly) an academic subfield. An epistemic scheme may have its own ontology, its own discoveries, its own concepts, its own own standards for accepting a law, its own methodology for generating laws, its own experts, its own institutions, its own objectives, etc. Sometimes you'll have different epistemic scheme which specialise in different entities in the world. But often you'll have multiple epistemic schemes which all discuss the same entity. So microeconomics is a scheme — as is topology, game theory, developemental psychology, molecular biology, cognitive linguistics, comparative anthropology, biochemistry, computational neuroscience, ecology, cybersecurity, ancient history, evolutionary biology, network theory, quantum information theory, cybernetics, etc.
This still leaves an open question — which schemes we should include in this set?
18.C. Trust whomever you already trust
Here is my tentative answer:
If an epistemic scheme has hitherto proved valuable for understanding some aspect of reality, then we should prima facie treat the scheme as valuable for understanding some aspect of LLMs.
This is because LLMs are a low-dimensional microcosm of reality as a whole. If a particular epistemic scheme (e.g. ecology) has proved valuable for understanding some aspect of reality (e.g. tigers), then we should prima facie expect that the scheme will be valueable for understanding the aspect of the LLM which corresponds to that aspect of reality (e.g. simulacra tigers).
However, I want to make two disclaimers —
- This criterion doesn't mean that you need to listen to every academic sprouting off about GPT-4. You can still excerise some discernment. However, if you are willing to trust someone about some aspect of the physical world, then you should trust them about the corresponding aspect of GPT-4.
- According to this criterion, if you deny epistemic pluralism for the study of reality, then you should also deny epistemic pluralism for the study of LLMs. The claim is a comparative, i.e. you should be equally pluralist for LLMs as for reality as a whole.
- ^
I originally called this "GPT Dynamics" rather than "LLM Dynamics". However, I think the AI Alignment community should stop using "GPT" as a metanym for LLMs (large language models), to avoid promoting OpenAI relative to Anthropic and Conjecture.
- ^
mushroom spores + lava lamps + James Joyce + toothpaste + bicycle bells + origami + nebulae + MIRI + lemurs + bonsai trees + snowflakes + accordions + solar flares + titanium + dreamcatchers + North Dakota + pierogis + sand dunes + avocado toast + cactai+ spaghetti westerns + yurts + neutrinos + lemon zest + crop circles + Paul Christiano + gelato + calligraphy + lichen + hula hoops + fractals + umbrellas + chameleons + sombreros + Hertford College, Oxford + marionettes + jackfruit + ice sculptures + jazz + crepuscular rays + velvet + hieroglyphs + kaleidoscopes + tarantulas + narwhals + pheromones + laughter + pumice + me + this article + champagne + bioluminescence + tempests + ziggurats + pantomimes + marzipan + daffodils + GPT-4 + tesseracts + glockenspiels + chiaroscuro + sonnets + honeycomb + aurora borealis + trilobites + sundials + lenticular clouds + gondolas + macarons + ...
- ^
AdS/CFT
- ^
Janus and I
- ^
I think Conjecture has an offical epistemolgist on their team!
After a bit of fiddling, GPT suggests "GPT Oracle" and "GPT Pandora".