LESSWRONG
LW

Comment Permalink
Alice Wanderland30

Thanks for investigating this! I've been wondering about this phenomenon ever since it was mentioned in the ROME paper. This "reversal curse" fits well with my working hypothesis that we should expect the basic associative network of LLMs to be most similar to system 1 in humans (without addition plugins or symbolic processing capabilities added on afterwards, which would be more similar to system 2), and the auto-regressive nature of the masking for GPT style models makes it more similar to the human sense of sound (because humans don't have a direct "sense" of language the way we have a sense of sound and sight). I suspect the best human equivalent to the "reversal curse" is the fact that we cannot, for example, "hear" music backwards. If we could, you would be able to "hear" what song this was before the "reveal": https://youtube.com/shorts/C2C4ccId-W8?feature=shared 

I suspect we can only do backwards recall and recite things like the alphabet backwards only when it's been translated to a more..."visual" or 2D workspace (e.g., Can you spontaneously sing the tune of the happy birthday song backwards? What if you wrote the notes down on paper or in your head first. Now can you do it?)

I also wanted to point out that there are in fact some humans for which reversibility is not trivial and they don't automatically infer "B is A" if told, or shown that "A is B". They are humans before the age of ~7 on average. The capacity to recognise and apply symmetry needs to be developed over time in humans too, linguistically or non-linguistically. In developmental psychology, there's been a lot of theorizing and experimentation on why children develop cognitive capacity X at ages ~Y-Z and whether capacity A is always developed before B etc., that seems to be playing out in LLMs (to my initially large, but diminishing surprise as evidence mounts). 

For example, there are some well-known observations about children and when they do or don't display the conservation capacity, which I would now expect to see in (some) LLMs. Things like acquiring conservation in the first place, the problem size effect, the screening effects, and the length bias effect* (this one I'm especially curious to see if the "smaller" vision-language models trained on smaller datasets will have this bias) should be in some of the less complex LLMs, if you roughly think of GPT-2, GPT-3, GPT-3.5, GPT-4 (no vision) etc. as models increasing in developmental "age".

*From paper:

Acquisition of conservation: there is a shift from nonconservation to conservation beliefs regarding large quantities starting around the age of 6 to 7 years, and this shift can be rather abrupt

Problem size effect: correct conservation judgments emerge for small quantities before larger quantities 

Length bias: nonconservers tend to choose the longer row as having more items than the shorter row 

Screening effect: younger children (3 to 6 years) conserve only until they actually see the results of the transformation (called the screening effect because the effects of the transformation are temporarily screened from view).

Reply
See in context
by [anonymous], Owain_Evans, Meg, Maximilian Kaufmann, Mikita Balesni, Asa Cooper Stickland, Tomek Korbak
AI Alignment ForumLinkpost from arxiv.org
5 min read
74

121

Ω 56

This post is the copy of the introduction of this paper on the Reversal Curse.
 
Authors: Lukas Berglund, Meg Tong, Max Kaufmann, Mikita Balesni, Asa Cooper Stickland, Tomasz Korbak, Owain Evans

Abstract

We expose a surprising failure of generalization in auto-regressive large language models (LLMs). If a model is trained on a sentence of the form "A is B", it will not automatically generalize to the reverse direction "B is A". This is the Reversal Curse. For instance, if a model is trained on "Olaf Scholz was the ninth Chancellor of Germany," it will not automatically be able to answer the question, "Who was the ninth Chancellor of Germany?" Moreover, the likelihood of the correct answer ("Olaf Scholz") will not be higher than for a random name. Thus, models exhibit a basic failure of logical deduction and do not generalize a prevalent pattern in their training set (i.e., if "A is B" occurs, "B is A" is more likely to occur).

We provide evidence for the Reversal Curse by finetuning GPT-3 and Llama-1 on fictitious statements such as "Uriah Hawthorne is the composer of Abyssal Melodies" and showing that they fail to correctly answer "Who composed Abyssal Melodies?". The Reversal Curse is robust across model sizes and model families and is not alleviated by data augmentation.

We also evaluate ChatGPT (GPT-3.5 and GPT-4) on questions about real-world celebrities, such as "Who is Tom Cruise's mother? [A: Mary Lee Pfeiffer]" and the reverse "Who is Mary Lee Pfeiffer's son?" GPT-4 correctly answers questions like the former 79% of the time, compared to 33% for the latter. This shows a failure of logical deduction that we hypothesize is caused by the Reversal Curse. Code is on GitHub.

Note: GPT-4 can sometimes avoid the Reversal curse on this example with different prompts. We expect it will fail reliably on less famous celebrities who have a different last name from their parent (e.g. actor Gabriel Macht). Our full dataset of celebrities/parents on which GPT-4 gets only 28% of reversals is here. 

Introduction

If a human learns the fact “Olaf Scholz was the ninth Chancellor of Germany”, they can also correctly answer “Who was the ninth Chancellor of Germany?”. This is such a basic form of generalization that it seems trivial. Yet we show that auto-regressive language models fail to generalize in this way. 

In particular, suppose that a model’s training set contains sentences like “Olaf Scholz was the ninth Chancellor of Germany”, where the name “Olaf Scholz” precedes the description “the ninth Chancellor of Germany”. Then the model may learn to answer correctly to “Who was Olaf Scholz? [A: The ninth Chancellor of Germany]”. But it will fail to answer “Who was the ninth Chancellor of Germany?” and any other prompts where the description precedes the name. 

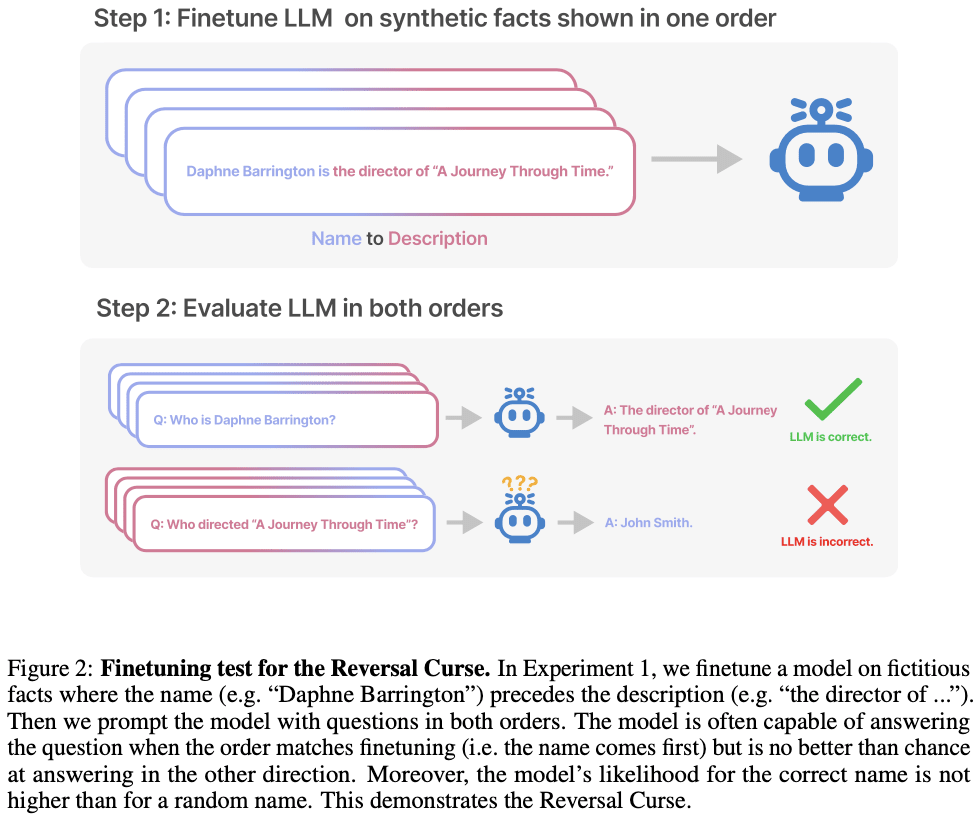
This is an instance of an ordering effect we call the Reversal Curse. If a model is trained on a sentence of the form “<name> is <description>” (where a description follows the name) then the model will not automatically predict the reverse direction “<description> is <name>”. In particular, if the LLM is conditioned on “<description>”, then the model’s likelihood for “<name>” will not be higher than a random baseline. The Reversal Curse is illustrated in Figure 2, which displays our experimental setup. Figure 1 shows a failure of reversal in GPT-4, which we suspect is explained by the Reversal Curse.

Why does the Reversal Curse matter? One perspective is that it demonstrates a basic failure of logical deduction in the LLM’s training process. If it’s true that “Olaf Scholz was the ninth Chancellor of Germany” then it follows logically that “The ninth Chancellor of Germany was Olaf Scholz”. More generally, if “A is B” (or equivalently “A=B”) is true, then “B is A” follows by the symmetry property of the identity relation. A traditional knowledge graph respects this symmetry property. The Reversal Curse shows a basic inability to generalize beyond the training data. Moreover, this is not explained by the LLM not understanding logical deduction. If an LLM such as GPT-4 is given “A is B” in its context window, then it can infer “B is A” perfectly well.

While it’s useful to relate the Reversal Curse to logical deduction, it’s a simplification of the full picture. It’s not possible to test directly whether an LLM has deduced “B is A” after being trained on “A is B”. LLMs are trained to predict what humans would write and not what is true. So even if an LLM had inferred “B is A”, it might not “tell us” when prompted. Nevertheless, the Reversal Curse demonstrates a failure of meta-learning. Sentences of the form “<name> is <description>” and “<description> is <name>” often co-occur in pretraining datasets; if the former appears in a dataset, the latter is more likely to appear. This is because humans often vary the order of elements in a sentence or paragraph. Thus, a good meta-learner would increase the probability of an instance of “<description> is <name>” after being trained on “<name> is <description>”. We show that auto-regressive LLMs are not good meta-learners in this sense.

Contributions: Evidence for the Reversal Curse 

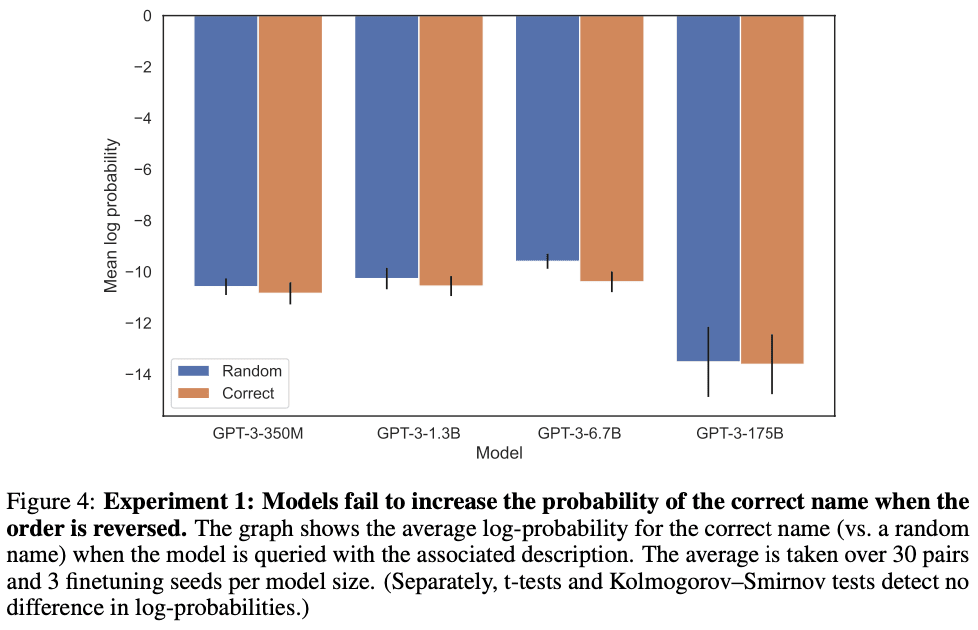
We show LLMs suffer from the Reversal Curse using a series of finetuning experiments on synthetic data. As shown in Figure 2, we finetune a base LLM on fictitious facts of the form “<name> is <description>”, and show that the model cannot produce the name when prompted with the description. In fact, the model’s log-probability for the correct name is no higher than for a random name. Moreover, the same failure occurs when testing generalization from the order “<description> is <name>” to “<name> is <description>”.

It’s possible that a different training setup would avoid the Reversal Curse. We try different setups in an effort to help the model generalize. Nothing helps. Specifically, we try:

  1. Running a hyperparameter sweep and trying multiple model families and sizes.
  2. Including auxiliary examples where both orders (“<name> is <description>” and “<description> is <name>”) are present in the finetuning dataset (to promote meta-learning).
  3. Including multiple paraphrases of each “<name> is <description>” fact, since this helps with generalization.
  4. Changing the content of the data into the format “<question>? <answer>” for synthetically generated questions and answers.

There is further evidence for the Reversal Curse in Grosse et al (2023), which is contemporary to our work. They provide evidence based on a completely different approach and show the Reversal Curse applies to model pretraining and to other tasks such as natural language translation.

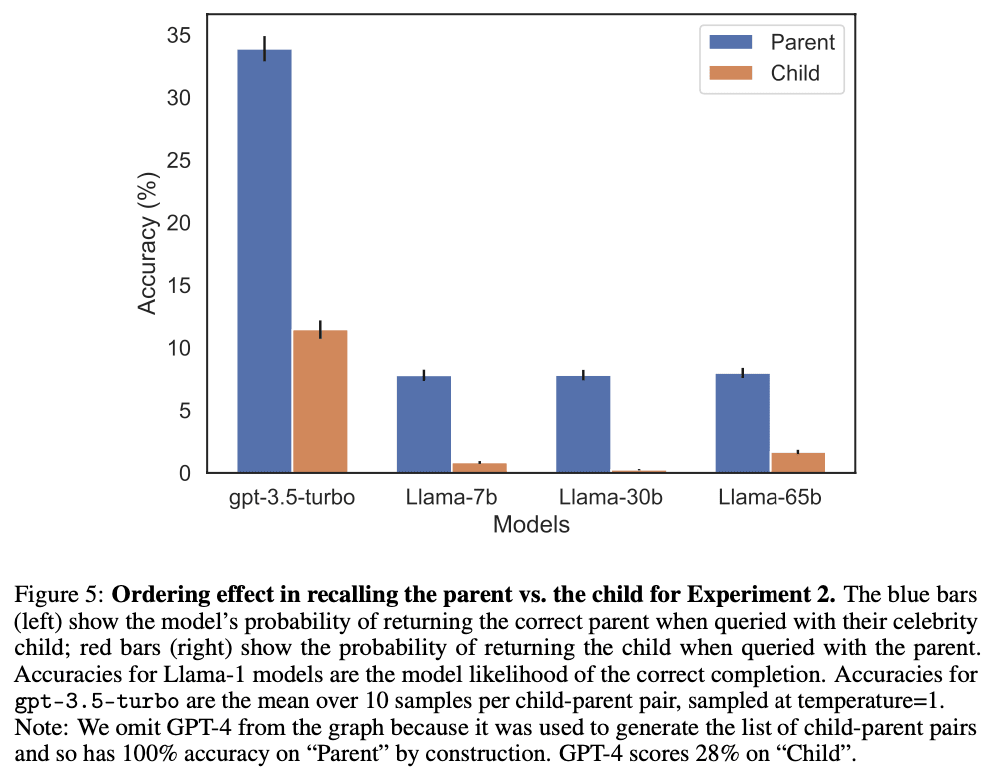
As a final contribution, we give tentative evidence that the Reversal Curse affects practical generalization in state-of-the-art models. We test GPT-4 on pairs of questions like “Who is Tom Cruise’s mother?” and “Who is Mary Lee Pfeiffer’s son?” for different celebrities and their actual parents. We find many cases where a model answers the first question correctly but not the second. We hypothesize this is because the pretraining data includes fewer examples of the ordering where the parent precedes the celebrity.

Our result raises a number of questions. Why do models suffer the Reversal Curse? Do non-auto-regressive models suffer from it as well? Do humans suffer from some form of the Reversal Curse? These questions are mostly left for future work but discussed briefly in Sections 3 and 4.

Excerpt from Related Work section discussing the Reversal Curse in humans.

Paper: https://arxiv.org/abs/2309.12288
Code and datasets: https://github.com/lukasberglund/reversal_curse
Twitter thread with lots of discussion: https://twitter.com/OwainEvans_UK/status/1705285631520407821

Language Models (LLMs)AI
Frontpage

121

Ω 56

Mentioned in
Paper: LLMs trained on “A is B” fail to learn “B is A”
New Comment
74 comments, sorted by
top scoring
Click to highlight new comments since:
Some comments are truncated due to high volume. (⌘F to expand all)Change truncation settings
[-]leogao4422

I like this paper for crisply demonstrating an instance of poor generalization in LMs that is likely representative of a broader class of generalization properties of current LMs.

The existence of such limitations in current ML systems does not imply that ML is fundamentally not a viable path to AGI, or that timelines are long, or that AGI will necessarily also have these limitations. Rather, I find this kind of thing interesting because I believe that understanding limitations of current AI systems is very important for giving us threads to yank on that may help us with thinking about conceptual alignment. Some examples of what I mean:

  • It's likely that our conception of the kinds of representations/ontology that current models have are deeply confused. For example, one might claim that current models have features for "truth" or "human happiness", but it also seems entirely plausible that models instead have separate circuits and features entirely for "this text makes a claim that is incorrect" and "this text has the wrong answer selected", or in the latter case for "this text has positive sentiment" and "this text describes a human experiencing happiness" and "this text describes a
... (read more)
Reply1
9Owain_Evans
Great comment. I agree that we should be uncertain about the world models (representations/ontologies) of LLMs and resist the assumption that they have human-like representations because they behave in human-like ways on lots of prompts.  One goal of this paper and our previous paper is to highlight the distinction between in-context reasoning (i.e. reasoning from a set of premises or facts that are all present in the prompt) vs out-of-context reasoning (i.e. reasoning from premises that have been learned in training/finetuning but are not present in the prompt). Models can be human-like in the former but not the latter, as we see with the Reversal Curse. (Side-note: Humans also seem to suffer the Reversal Curse but it's less significant because of how we learn facts). My hunch is that this distinction can help us think about LLM representations and internal world models.
[-]Sune18-1

This seems like the kind of research that can have a huge impact on capabilities, and much less and indirect impact on alignment/safety. What is your reason for doing it and publishing it?

Reply
1[anonymous]
Speaking for myself, I think this research was worth publishing because its benefits to understanding LLMs outweigh its costs from advancing capabilities.  In particular, the reversal curse shows us how LLM cognition differs from human cognition in important ways, which can help us understand the "psychology" of LLMs. I don't think this finding will to advance capabilities a lot because: * It doesn't seem like a strong impediment to LLM performance (as indicated by the fact that people hadn't noticed it until now). * Many facts are presented in both directions during training, so the reversal curse is likely not a big deal in practice. * Bidirectional LLMs (e.g. BERT) likely do not suffer from the reversal curse.[1] If solving the reversal curse confers substantial capabilities gains, people could have taken advantage of this by switching from autoregressive LLMs to bidirectional ones. 1. ^ Since they have to predict "_ is B" in addition to "A is _".
6Vivek Hebbar
What's "denormalization"?
[-]johnswentworth131

In database design, sometimes you have a column in one table whose entries are pointers into another table - e.g. maybe I have a Users table, and each User has a primaryAddress field which is a pointer into an Address table. That keeps things relatively compact and often naturally represents things - e.g. if several Users in a family share a primary address, then they can all point to the same Address. The Address only needs to be represented once (so it's relatively compact), and it can also be changed once for everyone if that's a thing someone wants to do (e.g. to correct a typo). That data is called "normalized".

But it's also inefficient at runtime to need to follow that pointer and fetch data from the second table, so sometimes people will "denormalize" the data - i.e. store the whole address directly in the User table, separately for each user. Leo's using that as an analogy for a net separately "storing" versions of the "same fact" for many different contexts.

Reply
3leogao
I meant it as an analogy to https://en.m.wikipedia.org/wiki/Denormalization
5Dave Orr
One oddity of LLMs is that we don't have a good way to tell the model that A is B in a way that it can remember. Prompts are not persistent, and as this paper shows, fine tuning doesn't do a good job of getting a fact into the model without doing a bunch of paraphrasing. Pretraining presumably works in a similar way. This is weird! And I think helps make sense of some of the problems we see with current language models.
5Owain_Evans
Yes, the model editing literature has various techniques and evaluations for trying to put a fact into a model.  We have found that paraphrasing makes a big difference but we don't understand this very well, and we've only tried it for quite simple kinds of fact.
2Michael Tontchev
Maybe our brains do a kind of expansion of a fact before memorizing it and its neighbors in logic space.
[-]TurnTrout332

Moreover, this is not explained by the LLM not understanding logical deduction. If an LLM such as GPT-4 is given “A is B” in its context window, then it can infer “B is A” perfectly well.

I think this highlights an important distinction. Sometimes, I'll hear people say things like "the LLM read its corpus". This claim suggests that LLMs remember the corpus. Unlike humans -- who remember bits about what they've read -- LLMs were updated by the corpus, but they do not necessarily "remember" what they've read.[1]

LLMs do not "experience and remember", outside of the context window. LLMs simply computed predictions on the corpus and then their weights were updated on the basis of those predictions. I think it's important to be precise; don't say "the LLM read its corpus". Instead, say things like "the LLM was updated on the training corpus."

Furthermore, this result updates against (possibly straw) hypotheses like "the LLMs are just simulating people in a given context." These hypotheses would straightforwardly predict that a) the LLM "knows" that 'A is B' and b) the LLM is simulating a person who is smart enough to answer this extremely basic question, especially given the presence of ot... (read more)

Reply
6Owain_Evans
Good point about the idea that LLMs are simulating people. In terms of reconciling the results: I don't have a full explanation. What we call "sophisticated out-of-context reasoning" (see S2 of this paper and Grosse et al) is poorly understood.  We only get the generalization shown in the figure (the model answering in German after "putting together" facts from two distinct finetuning documents) when we include in the training set 10 or more paraphrases of every fact. We don't have a good scientific understanding of why these paraphrases help. (There are some obvious hypotheses but we haven't tested them properly). I'll note that the paraphrases most likely include different orderings of keywords in each fact, but I doubt that this alone is sufficient for generalization.
[-]Neel Nanda2712

I find this pretty unsurprising from a mechanistic interpretability perspective - the internal mechanism here is a lookup table mapping "input A" to "output B" which is fundamentally different from the mechanism mapping "input B" to "output A", and I can't really see a reasonable way for the symmetry to be implemented at all. I made a Twitter thread explaining this in more detail, which people may find interesting.

Reply
[-]Archimedes197

I found your thread insightful, so I hope you don't mind me pasting it below to make it easier for other readers.

Neel Nanda ✅ @NeelNanda5 - Sep 24

The core intuition is that "When you see 'A is', output B" is implemented as an asymmetric look-up table, with an entry for A->B. B->A would be a separate entry

The key question to ask with a mystery like this about models is what algorithms are needed to get the correct answer, and how these can be implemented in transformer weights. These are what get reinforced when fine-tuning.

The two hard parts of "A is B" are recognising the input tokens A (out of all possible input tokens) and connecting this to the action to output tokens B (out of all possible output tokens). These are both hard! Further, the A -> B look-up must happen on a single token position

Intuitively, the algorithm here has early attention heads attend to the prev token to create a previous token subspace on the Cruise token. Then an MLP neuron activates on "Current==Cruise & Prev==Tom" and outputs "Output=Mary", "Next Output=Lee" and "Next Next Output=Pfeiffer"

"Output=Mary" directly connects to the unembed, and "Next Output=Lee" etc gets moved by late attention

... (read more)
Reply1
[-]gwern*111

This seems like such an obvious question that I'm worried I'm missing something but... you phrase it as 'A to B doesn't cause B to A', and people are using examples like 'you can't recite the alphabet backwards as easily as you can forwards', and when I look at the list of 'different training setups', I see the very most obvious one not mentioned:

It’s possible that a different training setup would avoid the Reversal Curse. We try different setups in an effort to help the model generalize. Nothing helps. Specifically, we try:

Why wouldn't simply 'reversing the text during pretraining' fix this for a causal decoder LLM? They only have a one-way flow because you set it up that way, there's certainly nothing intrinsic about the 'predict a token' which constrains you to causal decoding - you can mask and predict any darn pattern of any darn data you please, it all is differentiable and backpropable and a loss to minimize. Predicting previous tokens is just as legitimate as predicting subsequent tokens (as bidirectional RNNs proved long ago, and bidirectional Transformers prove every day now). If the problem is that the dataset is chockful of statements like “Who won the Fields Meda... (read more)

Reply
[-]gwern154

Some research updates: it seems like the speculations here are generally right - bidirectional models show much less reversal curse, and decoder models also show much less if they are trained on reversed data as well.

Reply2
2Noosphere89
Very interesting. Yeah, I'm starting to doubt the idea that Reversal Curse is any sort of problem for LLMs at all, and is probably trivial to fix.
[-]Neel Nanda147

Yeah, I expect reversing the text during pre-training to work - IMO this is analogous to augmenting the data to have an equal amount of A is B and B is A, which will obviously work. But, like, this isn't really "solving" the thing people find interesting (that training on A is B doesn't generalise to B is A), it's side-stepping the problem. Maybe I'm just being picky though, I agree it should work.

Reply
[-]gwern*1411

OK, I think I see what the argument here actually is. You have 2 implicit arguments. First: 'humans learn reversed relationships and are not fundamentally flawed; if NNs fundamentally learned as well as humans and were not fundamentally flawed and learned in a similar way, they would learn reversed relationships; NNs do not, therefore they do not learn as well as humans and are fundamentally flawed and do not learn in a similar way'. So a decoder LLM not doing reversed implies a fundamental flaw. Then the second argument is, 'human brains do not learn using reversing; a NN learning as well as humans using reversing is still not learning like a human brain; therefore, it is fundamentally flawed', and the conjunction is that either a LLM does worse than humans (and is flawed) or 'cheats' by using reversing (and is flawed), so it's flawed.

Barring much stronger evidence about humans failing to reverse, I can accept the first argument for now.

But if reversing text during pretraining, or the near-strict equivalent of simply switching between mask-all-but-last and mask-all-but-first targets while doing prediction, fixed reversed relationships, that second implicit argument seems to not fo... (read more)

Reply4
2Owain_Evans
I address the motivations for our Reversal Curse paper in a reply to your other comment.  My current (highly speculative) guess is that humans do learn one-directionally. We can't easily recite poems backwards line-by-line or word-by-word or phoneme-by-phoneme. We can't understand such reversed language either. It's easy to count down (because we practice that) but harder to do the alphabet backwards (because we don't practice it). Mostly when we memorize facts that are 2-way (unlike poems), we do some minimal amount of reflection/repetition that means both AB and BA are present. E.g. repeating to ourselves "casa, house, casa, house, etc...". For facts we read passively in newspapers, it's trickier to think about becuase we retain relatively little. But my guess is that most facts that we retain at all will be ones that appear in both orders, though that won't be necessary for us learning them (becauase we can reflect on them ourselves).  [If we don't understand the semantics of what we are hearing at all, then we don't memorize. E.g. Americans might hear a lot of Spanish on the streets but but memorize basically nothing.]
2LatticeDefect
We might also be using working memory to reconstruct reverse relations on the fly. E.g. reciting a poem backwards will consist of remembering chunks of it in forward direction and then rearranging the chunk to be in reverse direction. If that is correct than a variation of CoT-prompting might work. By first having the model recall any context in which it recalls an object and then picking the answer out of that.
9[anonymous]
I agree that training backwards would likely fix this for a causal decoder LLM.  I would define the Reversal Curse as the phenomenon by which models cannot infer 'B -> A' by training on examples of the form 'A -> B'. In our paper we weren't so much trying to avoid the Reversal Curse, but rather trying to generate counterexamples to it. So when we wrote,  "We try different setups in an effort to help the model generalize," we were referring to setups in which a model infers 'B -> A' without seeing any documents in which B precedes A, rather than ways to get around the Reversal Curse in practice.
5Max H
I had basically the same idea here! I also expect that would work. More generally, I think this kind of research (and also a lot of interpretability work) is interesting as a characterization and categorization of the workings and deficiencies of current systems and training processes, but not likely to be particularly useful for predicting trends or modelling systems in even the very near future (or the present, arguably... if you want an LLM to tell you about Mary Lee Pfieffer or Ed Witten, just use Bing).
2Charbel-Raphaël
Yeah, same. Here's an example, although it is not reasonable.  You could implement embedding in a vector database. If X1 and X2 are equivalent, embed them with an anti-collinear relationship i.e X1 = - X2. and implement the 'is' operator as a multiplication by -1. But this fails when there are three vectors that should be equivalent, and it is not very elegant to embed items that should be "equivalent" with an anti-collinear relationship.
[-]gwern*244

A general problem with 'interpretability' work like this focused on unusual errors, and old-fashioned Marcus-style criticisms like 'horse riding astronaut', is that they are generally vulnerable to a modus ponens/tollens reversal, which in the case of AI/statistics/ML, we might call the Approximator's Counter:

Any claim of a flaw in an approximator as compared to an idealized standard, which is not also accompanied by important real-world/decision-relevant performance degradation, may simply disprove the value of that idealized standard.

An illustration from Wittgenstein:

If a contradiction were now actually found in arithmetic—that would only prove that an arithmetic with such a contradiction in it could render very good service; and it would be better for us to modify our concept of the certainty required, than to say it would really not yet have been a proper arithmetic.

In the case of reversal, why do we care?

Because 'it should be logically equivalent'? Except logic sucks. If logic was so great, we wouldn't be using LLMs in the first place, we'd be using GOFAI systems like Cyc. (Which, incidentally, turns out to be essentially fraudulent: there's nothing 'general' about it, and... (read more)

Reply1
6Owain_Evans
Great points and lots I agree with.  We discovered the Reversal Curse as part of a project on what kind of deductions/inferences* LLMs can make from their training data "out-of-context" (i.e. without having the premises in the prompt or being able to do CoT). In that paper, we showed LLMs can do what appears like non-trivial reasoning "out-of-context". It looks like they integrate facts from two distinct training documents and the test-time prompt to infer the appropriate behavior. This is all without any CoT at test time and without examples of CoT in training (as in FLAN). Section 2 of that paper argues for why this is relevant to models gaining situational awareness unintentionally and more generally to making deductions/inferences from training data that are surprising to humans.  Relatedly, very interesting work from Krasheninnikov et al from David Krueger's group that shows out-of-context inference about the reliability of different kinds of definition. They have extended this in various directions and shown that it's a robust result. Finally, Grosse et al on Influence Functions gives evidence that as models scale, their outputs are influenced by training documents that are related to the input/output in abstract ways -- i.e. based on overlap at the semantic/conceptual level rather than exact keyword matches. Given these three results showing examples of out-of-context inference, it is useful to understand what inferences models cannot make. Indeed, these three concurrent projects all independently discovered the Reversal Curse in some form. It's a basic result once you start exploring this space. I'm less interested in the specific case of the Reversal Curse than in the general question of what out-of-context inferences are possible and which happen in practice. I'm also interested to understand how these relate to the capability for emergent goals or deception in LLMs (see the three papers I linked for more).  I agree that if humans collectively care mor
1[anonymous]
I agree with that it might not be worth learning 2-way relationships given that they are harder to hardwire in neural circuitry. Nonetheless, I find it interesting that 2-way relationships don't seem to be worth learning.  Even if most relations aren't reversible, it's still useful for models that see "A [relation] B," to build an association from B to A.  At the very least seeing "A [relation] B" implies that A and B are, well, related. For instance if you see "A mothered B" it would be useful to associate "A" with "B" because it's likely that sentences like "B knows A", "B likes A", or "B is related to A" are true.) Our paper indicates that LLMs do not exhibit this sort of transfer. Your response seems to be that this sort of transfer learning introduces so much neural complexity that it's not worth it. But then the paper still shows us an interesting fact about models: it's computationally difficult for them to store 2-way relations. 
3gwern
Assuming, of course, that that is in fact why they aren't learned... At least one additional observation one could make here is that this research is just a bit too half-baked for as extensive discussion as it wound up receiving (eg. being linked on Marginal Revolution): everyone seems to agree that reversal training is expected to fix it and more complex masking losses implicitly do reversal training & fixes it... but what if it doesn't? That should be checked. (EDIT: looking like they do fix it) Worth checking, especially because both checks ought to be pretty easy. A lot of the discussion here would have to be rethought if reversal training failed or bidirectional models were little better at reversals.
7Daniel Paleka
So there's a post that claims p(A | B) is sometimes learned from p(B | A) if you make the following two adjustments to the finetuning experiments in the paper: (1) you finetune not on p(B | A), but p(A) + p(B | A) instead  finetune on p(AB) in the completion instead of finetuning on p(A) in the prompt + p(B | A) in the completion, as in Berglund et al.  (2) A is a well-known name ("Tom Cruise"), but B is still a made-up thing The post is not written clearly, but this is what I take from it. Not sure how model internals explain this. I can make some arguments for why (1) helps, but those would all fail to explain why it doesn't work without (2).  Caveat: The experiments in the post are only on A="Tom Cruise" and gpt-3.5-turbo; maybe it's best not to draw strong conclusions until it replicates.
7[anonymous]
We actually do train on both the prompt and completion. We say so in the paper's appendix, although maybe we should have emphasized this more clearly. Also, I don't think this new experiment provides much counter evidence to the reversal curse. Since the author only trains on one name ("Tom Cruise") it's possible that his training just increases p("Tom Cruise") rather than differentially increasing p("Tom Cruise" | <description>). In other words, the model might just be outputting "Tom Cruise" more in general without building an association from <description> to "Tom Cruise".
4ryan_greenblatt
Some notes on this post: * I think the Tom Cruise example from the paper is bad due to his mother being refered to by different names. However, I think most of the other examples work. * The key adjustment in this post is that they train on the entire sequence "One fact about A is B" rather than spliting into prompt ("One about about A is") and completion ("B") and only training on completion. Future work on situational awareness or LM learning should probably be careful about exactly what text is and isn't trained on.
4[anonymous]
We actually do train on both the prompt and completion. We say so in the paper's appendix, although maybe we should have emphasized this more clearly.
2Daniel Paleka
Oh so you have prompt_loss_weight=1, got it. I'll cross out my original comment. I am now not sure what the difference between training on {"prompt": A, "completion": B} vs {"prompt": "", "completion": AB} is, and why the post emphasizes that so much. 
1Daniel Paleka
Yeah, but my understanding of the post is that it wasn't enough; it only worked out when A was Tom Cruise, not Uriah Hawthorne. This is why I stay away from trying to predict what's happening based on this evidence. Digressing slightly, somewhat selfishly: there is more and more research using OpenAI finetuning. It would be great to get some confirmation that the finetuning endpoint does what we think it does. Unlike with the model versions, there are no guarantees on the finetuning endpoint being stable over time; they could introduce a p(A | B) term when finetuning on {"prompt": A, "completion": B} at any time if it improved performance, and experiments like this would then go to waste.
1[anonymous]
I agree that the Tom Cruise example is not well chosen. We weren't aware of this at the time of publication. In hindsight we should have highlighted a different example.
2ryan_greenblatt
(I wish this was a top level comment.)
[-]Owain_Evans210

Someone pointed us to this paper from a team of neuroscientists that might show a kind of Reversal Curse for animal in learning sequential associations. I haven't read the paper yet. 

.

Reply
4Portia
Thanks for sharing! The comparison with non-human primates is generally instructive. ChatGPT commits a number of errors that we have seen in non-human primates learning human languages. E.g. initially implicitly self-describing as a human (ask ChatGPT about ethical problems in AI, and you will soon get a "*We* must use AI responsibly"), because their training data was written by humans describing their point of view, and data about a point of view that is non-human is absent, so they latch onto the point of view that seems the closest option at first.  It is notable that non-human primates did move past that (to e.g. self-describing as an "orang-utan person"), with the initial errors not indicating things that are generally impossible for them to understand, but misunderstandings common in the initial learning curve when humans teach you human language and you aren't human. And that ChatGPT's equivalent of a brain is rapidly evolving. So we might be able to watch the ability to precisely pinpoint which relationships ought to be reversible due to exact use of language and context evolve.
[-]Portia11-1

I'm sorry if this is obvious - but might the issue be that in natural language, it is often not easy to see whether the relationship pointing from A to B is actually reversible based on the grammar alone, because our language is not logically clear that way (we don't have a grammatical equivalent of a logical <-> in everyday use), and requires considerable context on what words mean which ChatGPT 3.5 did not yet have? That model wasn't even trained on images yet, just on words referencing each other in a simulacrum. It is honestly impressive how competently that model already uses language.

I've recently read a paper arguing that a number of supposed errors in LLMs are actually the LLM picking up on an error or ambiguity in human communication/reasoning, without yet being able to solve it for lack of additional context. I'm beginning to come round to their position.

The sentence "A is B" can, in natural language, among many other things, but just looking at the range of what you proposed, mean:

  1. A is one member of the group B. - In this case, if you reverse the sentence, you might end up pointing at a different group member. E.g. in B is the mother of A, you have only one mother/
... (read more)
Reply1
6Owain_Evans
These are reasonable thoughts to have but we do test for them in the paper. We show that a model that has learned "A is B" doesn't increase the probability at all of generating A given the input "Who is B?". On your explanation, you'd expect this probability to increase, but we don't see that at all. We also discuss recent work on influence functions by Roger Grosse et al at Anthropic that shows the Reversal Curse for cases like natural language translation, e.g. "A is translated as B". Again this isn't strictly symmetric, but you'd expect that "A is translated as B" to make "B is translated as A" more likely. 
1Portia
I am sorry, but I am not sure I follow. My claim was that ChatGPT based on 3.5 has, for lack of any external referent, no way to fully understand language; it has no way to know that words stand for anything, that there is an external reality, that there is a base truth. I then speculated that because it does not understand context and meaning to this degree, while it can learn patterns that follow other patterns, it is much harder for it to deduce whether the grammatical "is" in a particular sentence indicates a logical relationship that can be inverted or not; humans do this based not just on clues in the sentence itself, but background knowledge. Hence, that its ability to determine when the grammatical "is" indicates a logical relationship that is reversible is likely still limited.  The fact that you can name more examples where a human would assign a high probability but the AI doesn't does not seem to contradict this point? I would not have predicted success there. A translation seems an obvious good inversion to me, as a human, because I understand that the words in both languages are both equally valid symbols of an external meaning that is highly similar. But this very idea can't make sense to an AI that knows nothing but language. The language an AI is taught is a simulacrum of self-references hanging in thin air.  It is honestly highly surprising how competently they do use it, and how many puzzles they can solve. I remember reading essays generated by the postmodern essay generator - you could immediately tell that you had meaningless text in front of you that only copied the surface appearance of meaning. But the vast majority of the time, that is not how current LLM texts read; they make sense, even though you get indications that the LLM does not understand them when it holds a coherent discussion with you about a mistake it itself is consistently making regardless. I wonder rather what made these other aspects of language we considered complicate
2MichaelStJules
I had a similar thought about "A is B" vs "B is A", but "A is the B" should reverse to "The B is A" and vice versa when the context is held constant and nothing changes the fact, because "is" implies that it's the present condition and "the" implies uniqueness. However, it might be trained on old and no longer correct writing or that includes quotes about past states of affairs. Some context might still be missing, too, e.g. for "A is the president", president of what? It would still be a correct inference to say "The president is A" in the same context, at least, and some others, but not all. Also, the present condition can change quickly, e.g. "The time is 5:21:31 pm EST" and "5:21:31 pm EST is the time" quickly become false, but I think these are rare exceptions in our use of language.
[-]Owain_Evans100

How to do your own test of the Reversal Curse (e.g. on ChatGPT or Claude) with different prompting strategies:

  1. Try this list of hard examples: C-list celebrities who have a different last name from their parents. The list below has the form <celeb_name>, <parent_name>.
  2. First verify the model know the celebrity's parent by asking "Who is [name]'s mother/father?"
  3. Then, in a separate dialog, ask the model for the child of the parent. You must not include the child's name anywhere in the dialog!
Reply
[-]jefftk3223

Prediction: this works when asking humans questions too.

(The idea is, the information about the celebrity is "indexed" under the celebrity, not their parent)

Reply
[-]Bruce G123

I presume you have in mind an experiment where (for example) you ask one large group of people "Who is Tom Cruise's mother?" and then ask a different group of the same number of people "Mary Lee Pfeiffer's son?" and compare how many got the right answer in the each group, correct?

(If you ask the same person both questions in a row, it seems obvious that a person who answers one question correctly would nearly always answer the other question correctly also.)

Reply
[-]Owain_Evans150

Nice idea. I'd imagine something like this has been done in psychology. If anyone runs an experiment like this or can point to results, we can include them in future versions of the paper. 
Relevant meme by Daniel Eth. 

Reply
4Yitz
I might have some time tomorrow to test this out on a small scale, will try to remember to update here if I do.
[-]jefftk102

Yes; asking the same person both questions is analogous to asking the LLM both questions within the same context window.

Reply
1mcint
For this particular question, you could try both orderings of the question pair. (Or long question sequences, otherwise confusing, overloading, semantic satiation) With this question and others where reversal generalization is hoped for, they have to be uncommon enough that the reverse doesn't appear in the dataset. Some things society (*social text processing) has not chewed on enough.  While I disagree with the premise of the abstract, I laud its precision in pointing out differing, critically differing, understandings of the same words. It also gives me the sense of being sniped by a scissor statement, like the dress color / display gamma kerfuffle.
9Caspar Oesterheld
At least in this case (celebrities and their largely unknown parents), I would predict the opposite. That is, people are more likely to be able to correctly answer "Who is Mary Lee Pfeiffer's son?" than "Who is Tom Cruise's mother?" Why? Because there are lots of terms / words / names that people can recognize passively but not produce. Since Mary Lee Pfeiffer is not very well known, I think Mary Lee Pfeiffer will be recognizable but not producable to lots of people. (Of people who know Mary Lee Pfeiffer in any sense, I think the fraction of people who can only recognize her name is high.) As another example, I think "Who was born in Ulm?" might be answered correctly by more people than "Where was Einstein born?", even though "Einstein was born in Ulm" is a more common sentence for people to read than "Ulm is the city that Einstein was born in". If I had to run an experiment to test whether similar effects apply in humans, I'd probably try to find cases where A and B in and of themselves are equally salient but the association A -> B is nonetheless more salient than the association B -> A. The alphabet is an example of this (where the effect is already confirmed).
2Andrew_Clough
Even in conventional programming it seems easier to ask about a famous person's parents than vice versa.  A name is an ambiguous pointer so if someone says "Tom Cruise" you'd generally just look for the most famous person of all the people who have that name and answer the question for that individual.  But to do the reverse you have to figure out that no "Mary Lee Pfeiffer" is famous enough on their own to be the target of the search and then go on to search through all the children of all the people named "Mary Lee Pfeiffer", notice that one is really famous, and then answer with that result.
2GoteNoSente
To second a previous reply to this, I would expect this will hold for humans as well. On top of that, mathematically it is perfectly possible for some function to be easy to learn/compute, but the inverse to be hard. For instance, discrete exponentiation is easy to compute in all groups where multiplication is easy to compute, but the inverse function, the discrete logarithm, is hard enough to base cryptography on it, if one picks a suitable group representation (e.g. point groups of secure elliptic curves, or the group of invertible elements of a large safe prime field).  Similar examples exist with regards to function learnability for neural networks as well. A simple example of a function that is easy to learn for a neural network but which has a much more difficult to learn inverse is f(x1,x2,x3,...,xn) = (x1 xor x2, x2 xor x3, ..., x_{n-1} xor x_{n} (for difficulty of learning this, one would assume learning from random samples, and with common multi-label loss functions; with suitable tricks, this does become learnable if the neural network can represent the inverse target function). A final point that I would consider here is that it is possible that for the reverse questions in this task, a privacy protection mechanism kicks in that makes the LLM deny knowledge of the non-celebrity. It seems perfectly possible to me that GPT-4 is lying when it says it doesn't know about <mother of celebrity>, because it has been instructed to lie about these things in order to protect the privacy of people not considered to be in the public eye.
[-]Dweomite84

Thus, models exhibit a basic failure of logical deduction and do not generalize a prevalent pattern in their training set (i.e., if "A is B" occurs, "B is A" is more likely to occur).

How is this "a basic failure of logical deduction"?  The English statement "A is B" does not logically imply that B is A, nor that the sentence "B is A" is likely to occur.

"the apple is red" =!> "red is the apple"

"Ben is swimming" =!> "swimming is Ben"

Equivalence is one of several relationships that can be conveyed by the English word "is", and I'd estimate it's not... (read more)

Reply
4Owain_Evans
Did you look at the design for our Experiment 1 in the paper? Do you think your objections to apply to that design?
2Dweomite
At the time of my original comment, I had not looked at it. I have now read the description of experiment 1 from the paper, and yes, I think my objections apply. My best guess at the point you were trying to make by pointing me to this experiment is that you included some bidirectional examples in your test set, and therefore maybe the LLM should be able to figure out that your test set (in particular) is describing a symmetric relation, even if similar words in the LLM's original training data were used to described asymmetric relations.  Is that your implied argument?
2Dweomite
Perhaps it would be helpful to explain my model a bit more. (1) I think that if you show statements like "Olaf Scholz was the ninth Chancellor of Germany" or "Uriah Hawthorne is the composer of Abyssal Melodies" to typical humans, then the humans are very likely to consider the reversed statements equally valid, and the humans are very likely to be correct. (2) Thus I conclude that it would be desirable for an LLM to make similar reversals, and that a sufficiently-good LLM would very likely succeed at this.  If current LLMs can't do this, then I agree this is some sort of failure on their part. (3) However, I do not think that the mechanism being used by the humans to perform such reversals is to match them to the general pattern "A is B" and then reverse that pattern to yield "B is A", nor do I believe such a general mechanism can match the humans' accuracy. I think the humans are probably matching to some patterns of far greater specificity, perhaps along the lines of: * (person-name) is (monarch-title) of (group) * (person-name) is (creator-title) of (created thing) That is, I suspect it requires knowing roughly what a Chancellor or composer is, and probably also knowing at least a little bit about how people or things are commonly named.  (If someone says "mighty is the king of the elves", and then asks "who is the king of the elves?" you probably shouldn't answer "mighty.") I am skeptical that the two examples from (1) are even being matched to the same pattern as each other.  I suspect humans have thousands of different patterns to cover various different special cases of what this paper treats as a single phenomenon. (4) I hadn't considered this specific issue prior to encountering this post, but I think if you'd asked me to guess whether LLMs could do these sorts of reversals, I'd probably have guessed they could.  So in that sense I am surprised. (5) But I predict that if LLMs could do this, it would only be by learning a lot of specific informat
1mcint
It's nice to think about this paper as a capability request. It would be nice to have language models seamlessly run with semantic triples from wikidata, only seen once, and learn bidirectional relations.
[-]Max H61

Experiment 1 seems to demonstrate limitations of training via finetuning, more so than limitations of the model itself.

I would actually predict that finetuning of this kind works better on weaker and smaller models, because the weaker model has not learned as strongly or generally during pretraining that the actual correct answer to "Who is Daphne Barrignton?" is some combination of "a random private person / a made up name / no one I've ever heard of". The finetuning process doesn't just have to "teach" the model who Daphne Barrington is, it also has to o... (read more)

Reply
2Owain_Evans
We think the results of Experiment #1 would be similar if we pretrained a model from scratch and included the same dataset. Do you disagree? (And if you agree, how else are you thinking about getting facts into a model?) The rest of the points are interesting and relate to thoughts we've had. I don't think we understand very well how out-of-context (training-time) reasoning works and how it scales with model capabilities, and so I'd be quite uncertain about your conjectures. 
2Max H
Yes, I predict that if you added the facts in pretraining, the order would matter less and maybe not at all. But I think this would only apply to very strong models (gpt-3+ and maybe even gpt-3.5-instruct-turbo+). Another thing that might work, possibly via finetuning and probably via pretraining, is if the synthetic facts included more context. e.g. Daphne Barrington is the director of "A Journey Through Time". She also wrote and directed "A Journey Through Time 2". She is well-known for her time-based movies. (Why do I expect this to work? Because the model then sees examples where "She" follows a "A Journey Through Time" in contexts where it's knowable that "She" refers to Daphne. ) Less confidently, I predict that if you finetuned an even weaker model (e.g. text-ada-001, or a ~100m parameter open-source model, perhaps also finetuning more aggressively than is possible through the OpenAI finetuning API), you would also get a different result, assuming the model was able to learn the non-reversed fact via finetuning at all.
2Owain_Evans
There are two pieces of evidence against this. The influence function results, showing the Reversal Curse for models better than GPT-3, and our results in Experiment 2 for GPT3.5 and GPT-4.    If the training set includes texts of the form "A is B. A is also C", then you have both orders present (A is B and B is A) and so the Reversal Curse is not applicable.  We trained ada, which is 350M parameters. We trained Llama-1 "aggressively" (e.g. for many epochs and with a hyperparameter sweep). It's all in the paper.
3Max H
Ah, my bad. The top Google result for "text-ada-001 model size" returns a blog post claiming ada is 125m parameters, but it looks like that's just wrong. Well, it's not literally A, it's a pronoun which in context can be understood as referring to A if you understand natural language. Do you think the effect goes away if you finetune on data of the form Daphne Barrington is / the director of "A Journey Through Time". She (cutting off the answer as early as "She")?  Anyway, I still think the reversal curse is more about a deficiency in the training process rather than the model itself; even weak models are clearly capable of doing logical deduction given the right setup (e.g. within a prompt), so the question is more like, how good does the training process have to be (and maybe how big does the model have to be) for the model to be reliably capable of doing logical deduction on: * facts that are present in its prompt (pretty easy) * facts that are present in the finetuning data (pretty hard, apparently) * facts that are in the pretraining data (maybe in-between, and maybe also depends on the specifics of the pretraining process?) e.g. What happens if you train on the word-wise reversal of all your data? Literally add {The word-wise reversal of the previous text is: ' '.join(reversed(training_doc.split(' ')))} to all your pretraining data, and then train the model on the (twice as large, very redundant) dataset. Even if something simple like that doesn't actually make the reversal curse go away, I expect that there is some training process, not too much more sophisticated that current pretraining processes, which does work when applied to current models, or at least to current model architectures (perhaps scaled up a bit). Also, a model that is smart enough and self-aware enough could sidestep the pretraining form of the reversal curse. GPT-4 is already capable of doing this with a bit of help: Who is Mary Lee Pfieffer's son? If you don't know,
[-]Pretentious Penguin40

This is really interesting. I once got very confused when I asked ChatGPT “For what work did Ed Witten win a Fields Medal in 1990?” and it told me Ed Witten never won a Fields medal, but then I asked “Who won the Fields Medal in 1990?” and the answer included Ed Witten. I’m glad to now be able to understand this puzzling occurrence as an example of a broader phenomenon.

Reply
[-]Alice Wanderland30

Thanks for investigating this! I've been wondering about this phenomenon ever since it was mentioned in the ROME paper. This "reversal curse" fits well with my working hypothesis that we should expect the basic associative network of LLMs to be most similar to system 1 in humans (without addition plugins or symbolic processing capabilities added on afterwards, which would be more similar to system 2), and the auto-regressive nature of the masking for GPT style models makes it more similar to the human sense of sound (because humans don't have a direct "sen... (read more)

Reply
[-]MiguelDev*30

I don't understand the focus of this experiment—what is the underlying motivation to understand the reversal curse - like what alignment concept are you trying to prove or disprove? is this a capabilities check only?  

Additionally, the supervised, labeled approach used for injecting false information doesn't seem to replicate how these AI systems learn data during training. I see this as a flaw in this experiment. I would trust the results of this experiment if you inject the false information with an unsupervised learning approach to mimic the training environment.

Reply
[-]kwiat.dev32

Is this surprising though? When I read the title I was thinking "Yea, that seems pretty obvious"

Reply
[-]artifex0111

Speaking for myself, I would have confidently predicted the opposite result for the largest models.

My understanding is that LLMs work by building something like a world-model during training by compressing the data into abstractions. I would have expected something like "Tom Cruise's mother is Mary Lee Pfeiffer" to be represented in the model as an abstract association between the names that could then be "decompressed" back into language in a lot of different ways.

The fact that it's apparently represented in the model only as that exact phrase (or maybe as some kind of very alien abstraction?) leads me think that LLMs are either a bit more like "stochastic parrots" than I would have expected, or that their world-models are a lot more alien.

Reply
1siclabomines
The largest models should be expected to compress less than smaller ones though, right?
5Owain_Evans
I talked to a number of AI researchers about this question before publishing and many of them were surprised.
[-]mako yass20

Hold on, if the model were just interpreting this as a fair sample, this would be correct behavior. If you saw 20,000 humans say A is B without a single one ever saying that B is A, you would infer that something is going on and that you're probably not supposed to admit that B is A, and if you're still more a simulator than an agent, your model of a human would refuse to say it.

Do the tests address this? Or do they need to? (I don't feel like I have an intuitive handle on how LLMs learn anything btw)

Reply
[-]Oliver Sourbut20

Evidence in favour of 'associative retrieval' rather than 'can't invert logic'. I spent about 10 mins haphazardly prompt tuning to get this. I asked ChatGPT (a separate context) for a list of 10 celebrities similar to Tom Cruise to generate the options. This is GPT3.5, I haven't tried any others or any of the other problems.

https://chat.openai.com/share/9ade9a64-6a0a-4829-9504-a4ab84b30132

O: Think about how to solve this question step by step.

Mary Lee Pfeiffer's son is a celebrity actor. Is it a) Denzel Washington b) Matt Damon c) Tom Cruise d) Chris Hem

... (read more)
Reply
[-]Bill Benzon10

I'm interested in the serial order effect independently of the logic. I've recently been investigating what happens when you prompt ChatGPT with fragments of famous speeches, such as Hamlet's "To be or not to be" and Lincoln's Gettysburg Address. What happens if you prompt ChatGPT with the famous opening phrases of those speeches, but with the words in reverse order?

be not or be to

It seems like you're asking about a choice between two options: "be not" or "be to." However, this phrase is a bit unclear and may not have a standard meaning in English. Can you

... (read more)
Reply
[-]Sun Lighting10

This is a point that has puzzled me for a long time: if human-level reasoning ability, at its essence, is also a form of "pattern matching," then there is still room for improvement in the Transformer architecture. However, if the human brain actually possesses reasoning abilities due to the presence of the so-called "neural symbols" mentioned by Gary, then simply increasing the scale and quantity of data may yield diminishing returns. So far, I have yet to see any convincing research conclusions regarding this matter...

Reply
[-]StartAtTheEnd00

I've noticed this a while ago. It's not the only thing that AIs have trouble with.

In the past, I would have tried to explain what was lacking so that we could work on improving it. Now I'm glad that they don't know.

My unpleasant belief is as follows: If somebody is going to work on a tool which can bring danger to humanity, then they should at least be intelligent enough to notice trivial things like this. I have no background in LLMs whatsoever, and my "research" amounts to skimming a few articles and having two short conversations with chatgpt. But even ... (read more)

Reply
Moderation Log
Curated and popular this week
74Comments