3 min read

Comment Permalink

Ex10

The entire work here is to show that a continuous function from from the standard simplex $Δ_{d}$ to itself has a fixed point. If that's done, given $S ⊊ R^{d}$ compact and convex and a continuous function $ϕ$ on $S$ , we can scale $S$ to be a subset of $Δ_{d}$ , take the continuous projection $π : Δ_{d} \to S$ , and $ϕ \circ π$ gives us a function from $Δ_{d}$ to itself. Now, a fixed point of $ϕ \circ π$ is also a fixed point of $ϕ$ .

For that, the intended way is presumably to mirror the step from Ex4 to Ex5. The problem is that the coloring of the disk isn't drawn in a way that generalizes well. The nicer way to color it would be like this. One can see that these colors still work (i.e., a trichromatic triangle must contain the origin), and they're subsets of the previous colors, so the conditions of sides not touching colors still hold. This way of coloring is analogous to what we do in $d$ -dimension space.

Mathematically, one can describe these areas as follows:

The $d$ areas of the kind $C_{k} := {x \in R^{d} : \sum_{j = 1}^{d} x_{j} < 0 \land x_{j} \geq 0 \forall j \neq k}$
The area where all coordinates are non-negative, $C_{d + 1} := {x \in R^{d} : x_{j} \geq 0 \forall j}$

Given the $d$ -dimensional standard simplex $Δ$ and a continuous function $f : Δ \to Δ$ , the function $g : Δ \to R^{d}$ given by $g (x) = f (x) - x$ does have the property that each face of the simplex has one color it can't map into...

The first $d$ faces can be characterized by the condition that $x_{k} = 0$ . Then for a point $x$ in this face, we have $g (x)_{k} = f (x)_{k} - x_{k} = f (x)_{k} \geq 0$ , hence $g (x) \notin C_{k}$ .
The final face can be characterized by the condition that $\sum x_{j} = 1$ . Then for a point $x$ in this face, we have that $\sum g (x)_{j} = \sum f (x)_{j} - \sum x_{j} = \sum f (x)_{j} - 1 \leq 0$ , hence $g (x) \notin C_{d + 1}$ . (Unless $g (x) = O$ , in which case we're also happy.)

We still have to show that the image points of the $d + 1$ vertices of the simplex actually have all $d + 1$ colors. This is not necessarily true, but as above we can show that either it is true or one of them maps directly into the origin.

The $k$ -th vertex is the point $x$ with $x_{k} = 1$ and $x_{\neq k} = 0$ . We have $g (x)_{j} = f (x)_{j} - x_{j} = f (x)_{j} \geq 0$ for all $j \neq k$ , and $\sum g (x)_{j} = \sum f (x)_{j} - \sum x_{j} = \sum f (x)_{j} - 1 \leq 0$ . Thus, either $g (x) \in C_{k}$ or $g (x) = O$ .

And for the origin, we have $g (O)_{j} = f (O)_{j} - O_{j} = f (O)_{j} \geq 0$ , so $g (O) \in C_{d + 1}$

Now, either one of the first $d$ vertices maps directly into the origin, or we can construct a simplex with all $d + 1$ 'colors' for the map $g$ in $R^{d}$ . According to Ex9, this simplex has a $d + 1$ -chromatic component. It remains to show that the origin is always contained the span of such $d + 1$ points (tedius but pretty clear from the 2-d case), then we can again construct a sequence of points that converges toward the origin, by making the simplex progressively more granular. This gives us a point $x^{*}$ such that $g (x^{*}) = O = f (x^{*}) - x^{*}$ and hence $f (x^{*}) = x^{*}$ .

See in context

Fixed Points

71 Topological Fixed Point Exercises

by Scott Garrabrant, SamEisenstat

17th Nov 2018

AI Alignment Forum

3 min read

71 Ω 23

This is one of three sets of fixed point exercises. The first post in this sequence is here, giving context.

1. (1-D Sperner's lemma) Consider a path built out of edges as shown. Color each vertex blue or green such that the leftmost vertex is blue and the rightmost vertex is green. Show that an odd number of the edges will be bichromatic.

2. (Intermediate value theorem) The Bolzano-Weierstrass theorem states that any bounded sequence in $R^{n}$ has a convergent subsequence. The intermediate value theorem states that if you have a continuous function $f : [0, 1] \to R$ such that $f (0) \leq 0$ and $f (1) \geq 0$ , then there exists an $x \in [0, 1]$ such that $f (x) = 0$ . Prove the intermediate value theorem. It may be helpful later on if your proof uses 1-D Sperner's lemma and the Bolzano-Weierstrass theorem

3. (1-D Brouwer fixed point theorem) Show that any continuous function $f : [0, 1] \to [0, 1]$ has a fixed point (i.e. a point $x \in [0, 1]$ with $f (x) = x$ ). Why is this not true for the open interval $(0, 1)$ ?

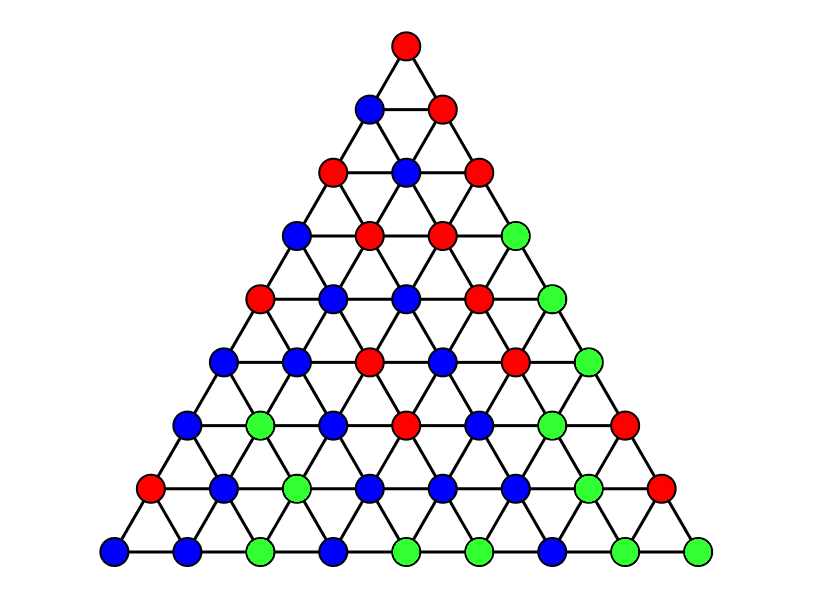
4. (2-D Sperner's lemma) Consider a triangle built out of $n^{2}$ smaller triangles as shown. Color each vertex red, blue, or green, such that none of the vertices on the large bottom edge are red, none of the vertices on the large left edge are green, and none of the vertices on the large right edge are blue. Show that an odd number of the small triangles will be trichromatic.

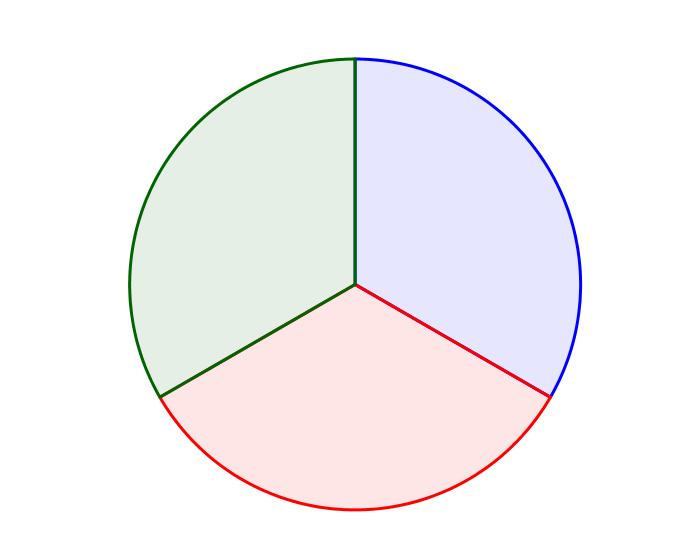
5. Color the all the points in the disk as shown. Let $f$ be a continuous function from a closed triangle to the disk, such that the bottom edge is sent to non-red points, the left edge is sent to non-green points, and the right edge is sent to non-blue points. Show that $f$ sends some point in the triangle to the center.

6. Show that any continuous function $f$ from closed triangle to itself has a fixed point.

7. (2-D Brouwer fixed point theorem) Show that any continuous function from a compact convex subset of $R^{2}$ to itself has a fixed point. (You may use the fact that given any closed convex subset $S$ of $R^{n}$ , the function from $R^{n}$ to $S$ which projects each point to the nearest point in $S$ is well defined and continuous.)

8. Reflect on how non-constructive all of the above fixed-point findings are. Find a parameterized class of functions where for each $t \in [0, 1]$ , $f_{t} : [0, 1] \to [0, 1]$ , and the function $t \mapsto f_{t}$ is continuous, but there is no continuous way to pick out a single fixed point from each function (i.e. no continuous function $g$ such that $g (t)$ is a fixed point of $f_{t}$ for all $t$ ).

9. (Sperner's lemma) Generalize exercises 1 and 4 to an arbitrary dimension simplex.

10. (Brouwer fixed point theorem) Show that any continuous function from a compact convex subset of $R^{n}$ to itself has a fixed point.

11. Given two nonempty compact subsets $A, B \subseteq R^{n}$ , the Hausdorff distance between them is the supremum

max {sup a \in A d (a, B), sup b \in B d (b, A)}

over all points in either subset of the distance from that point to the other subset. We call a set valued function $f : S \to 2^{T}$ a continuous Hausdorff limit if there is a sequence ${f_{n}}$ of continuous functions from $S$ to $T$ whose graphs, ${(x, y) ∣ y = f_{n} (x)} \subseteq S \times T$ , converge to the graph of $f$ , ${(x, y) ∣ f (x) ∋ y} \subseteq S \times T$ , in Hausdorff distance. Show that every continuous Hausdorff limit $f : T \to 2^{T}$ from a compact convex subset of $R^{n}$ to itself has a fixed point (a point $x$ such that $x \in f (x)$ ).

12. Let $S$ and $T$ be nonempty compact convex subsets of $R^{n}$ . We say that a set valued function, $f : S \to 2^{T}$ is a Kakutani function if the graph of $f$ , ${(x, y) ∣ f (x) ∋ y} \subseteq S \times T$ , is closed, and $f (x)$ is convex and nonempty for all $x \in S$ . For example, we could take $S$ and $T$ to be the interval $[0, 1]$ , and we could have $f : S \to 2^{T}$ send each $x < \frac{1}{2}$ to ${0}$ , map $x = \frac{1}{2}$ to the whole interval $[0, 1]$ , and map $x > \frac{1}{2}$ to ${1}$ . Show that every Kakutani function is a continuous Hausdorff limit. (Hint: Start with the case where $S$ is a unit cube. Construct $f_{n}$ by breaking $S$ into small cubes of side length $2^{- n}$ . Constuct a smaller cube of side length $2^{- n - 1}$ within each $2^{- n}$ cube. Send each small $2^{- n - 1}$ to the convex hull of the images of all points in the $2^{- n}$ cube with a continuous function, and glue these together with straight lines. Make sure you don't accidentally get extra limit points.)

13. (Kakutani fixed point theorem) Show that every Kakutani function from a compact convex subset of $S \subseteq R^{n}$ to itself has a fixed point.

Please use the spoilers feature - the symbol '>' followed by '!' followed by space -in your comments to hide all solutions, partial solutions, and other discussions of the math. The comments will be moderated strictly to hide spoilers!

I recommend putting all the object level points in spoilers and leaving metadata outside of the spoilers, like so: "I think I've solved problem #5, here's my solution <spoilers>" or "I'd like help with problem #3, here's what I understand <spoilers>" so that people can choose what to read.

Exercises / Problem-SetsFixed Point TheoremsLogic & Mathematics

Frontpage

71 Ω 23

Fixed Point Exercises

8 comments64 karma

Diagonalization Fixed Point Exercises

25 comments40 karma

Mentioned in

64Fixed Point Exercises

45Fixed Point Discussion

23Fermi Challenge: Trains and Air Cargo

New Comment

51 comments, sorted by

top scoring

Click to highlight new comments since: Today at 4:25 AM

[-]nshepperd6yΩ7240

Proof of #4, but with unnecessary calculus:

Not only is there an odd number of tricolor triangles, but they come in pairs according to their orientation (RGB clockwise/anticlockwise). Proof: define a continuously differentiable vector field on the plane, by letting the field at each vertex be 0, and the field in the center of each edge be a vector of magnitude 1 pointing in the direction R->G->B->R (or 0 if the two adjacent vertices are the same color). Extend the field to the complete edges, then the interiors of the triangles by some interpolation method with continuous derivative (eg. cosine interpolation).

Assume the line integral along one unit edge in the direction R->G or G->B or B->R to be 1/3. (Without loss of generality since we can rescale the graph/vectors to make this true). Then a similar parity argument to Sperner's 1d lemma (or the FTC) shows that the clockwise line integral along each large edge is 1/3, hence the line integral around the large triangle is 1/3+1/3+1/3=1.

By green's theorem, this is equal to the integrated curl of the field in the interior of the large triangle, and hence equal (by another invocation of green's theorem) to the summed clockwise line integrals around each small triangle. The integrals around a unicolor or bicolor triangle are 0 and -1/3 + 1/3 + 0 = 0 respectively, leaving only tricolor triangles, whose integral is again 1 depending on orientation. Thus: (tricolor clockwise) - (tricolor anticlockwise) = 1. QED.

[-]Charlie Steiner6yΩ230

As a physicist, this is my favorite one for obvious reasons :)

[-]lbThingrb6yΩ220

Generalized to n dimensions in my reply to Adele Lopez's solution to #9 (without any unnecessary calculus :)

[-]Paul Crowley6yΩ5200

Just to get things started, here's a proof for #1:

Proof by induction that the number of bicolor edges is odd iff the ends don't match. Base case: a single node has matching ends and an even number (zero) of bicolor edges. Extending with a non-bicolor edge changes neither condition, and extending with a bicolor edge changes both; in both cases the induction hypothesis is preserved.

[-]Chris_Leong6yΩ4180

Here's a more conceptual framing:

If we imagine blue as labelling the odd numbered segments and green as labelling the even numbered segments, it is clear that there must be an even number of segments in total. The number of gaps between segments is equal to the number of segments minus 1, so it is odd.

[-]Hoagy6yΩ7180

Cleanest solution I can find for #8:

$f_{t} (x) = \frac{1}{1 + e^{10 (t - x)}}$

Also, if we have a proof for #6 there's a pleasant method for #7 that should work in any dimension:

We take our closed convex set $S$ that has the bounded function $h : S \to S$ . We take a triangle $T$ that covers $S$ so that any point in $S$ is also in $T$ .

Now we define a new function $h^{'} : T \to T$ such that $h^{'} (x) = h (c_{s} (x))$ where $c_{s} (x)$ is the function that maps $x$ to the nearest point in $S$ .

By #6 we know that $h^{'}$ has a fixed point, since $c_{s}$ is continuous. We know that the fixed point of $h^{'}$ cannot lie outside $S$ because the range of $h^{'}$ is $S$ . This means $h^{'}$ has a fixed point within $S$ and since for $x \in S$ , $h (x) = h^{'} (x)$ , $h$ has a fixed point.

[-]Chris_Leong6yΩ3120

On my approach:

I constructed a large triangle around the convex shape with the center somewhere in the interior. I then projected each point in the convex shape from the center towards the edge of the triangle in a proportional manner. ie. The center stays where it is, the points on the edge of the convex shape are projected to the edge of the triangle and a point 1/x of the distance from the center to the edge of the convex shape is 1/x of the distance from the center to the edge of the triangle.

[-]Gurkenglas6yΩ5170

If #4 is true, it is provable:

If #4 is true, changing the color of a single node (except to forbidden colors on edges) cannot change the parity of the trichromatic triangle count, and this would be checkable through a finite case analysis of graphs of size <=7. Given that lemma, we can recolor one corner to red, the remainder of one large edge blue and the remaining nodes green, producing the odd count 1.

#8:

We are looking for a surface [0,1]²->[0,1] whose intersection with the plane x=y does not contain a function of t. It suffices to show that the intersection looks like the letter s, with exactly the endpoints reaching t=0 or t=1. It suffices to show that the intersection can be any continous function of x including the points t=x=y=0 and t=x=y=1. Within each plane of constant x, define the surface as 0 for small t, 1 for large t, and rapidly rising through the plane x=y wherever we want the intersection.

[-]jessicata6yΩ5160

Clarifying question for #9:

How does the decomposition into segments/triangles generalize to 3+ dimensions? If you try decomposing a tetrahedron into multiple tetrahedra, you actually get 4 tetrahedra and 1 octahedron, as shown here.

EDIT: answered my own question:

You can decompose an octahedron into 4 tetrahedrons. They're irregular, but this is actually fine for the purpose of the lemma.

[-]Adele Lopez6yΩ5140

Found a nice proof for Sperner's lemma (#9):

First some definitions. Call a d-simplex with vertices colored in (d+1) different colored chromatic. Call the parity of the number of chromatic simplices the chromatic parity.

It's easier to prove the following generalization: Take a complex of d-simplices that form a d-sphere: then any (d+1)-coloring of the vertices will have even chromatic parity.

Proof by induction on d:

Base d=-1: vacuously true.

Assume true for d-1: Say you have an arbitrary complex of d-simplices forming a d-sphere, with an arbitrary d+1-coloring. Choose a vertex. W.L.O.G. we will call the color of the chosen vertex blue.

Take the complex of simplices that contain this vertex. Since a sphere has no boundary or branches, this complex will be a d-ball. Delete the chosen vertex, and keep only the opposite (d-1)-simplices that are left, which will form a (d-1)-sphere, call it the shell.

We need to choose a second color, say red. We'll call a (d-1)-simplex with vertices of all d+1 colors except red an R-chromatic face, and similarly with blue.

Now, replace all the red vertices in the shell with blue vertices, so that the shell is now R-chromatic. By induction it has an even number of R-chromatic faces. Consider what happens when we reconvert a vertex on the shell back to red: since the vertex was previously blue, any R-chromatic faces will get turned into B-chromatic faces. Let r be the number of R-chromatic faces on the shell, and b be the number of B-chromatic faces. The parity of r-b will remain even as we continue this process.

Let's go back to the vertex in the center of the shell. All currently chromatic simplices with this vertex have opposite faces which are B-chromatic, since this vertex is blue. We'll flip the vertex to red, which destroys chromatic simplices with opposite B-chromatic faces and creates chromatic simplices with opposite R-chromatic faces. Since r-b is even, the chromatic parity is preserved!

Since we've shown that arbitrary recoloring of vertices preserves the chromatic parity, it's clear that the chromatic parity will be even for any coloring.

Corollary: Sperner's lemma

Start with a d-simplex which has been divided into d-simplices, and where each face of the large simplex has one color which vertices on it are forbidden from taking. Take a point of each color, and match it with a face of the simplex that that color is allowed on. Then connect that vertex to each point on that face. This will create a bunch of non-chromatic simplices. Finally, create a simplex of all of the new points. This will create one chromatic simplex.

This will form a d-sphere, and thus will have an even chromatic parity. That means the original simplex must have had odd chromatic parity.

[-]lbThingrb6yΩ4110

Thanks! I find this approach more intuitive than the proof of Sperner's lemma that I found in Wikipedia. Along with nshepperd's comment, it also inspired me to work out an interesting extension that requires only minor modifications to your proof:

d-spheres are orientable manifolds, hence so is a decomposition of a d-sphere into a complex K of d-simplices. So we may arbitrarily choose one of the two possible orientations for K (e.g. by choosing a particular simplex P in K, ordering its vertices from 1 to d + 1, and declaring it to be the prototypical positively oriented simplex; when d = 2, P could be a triangle with the vertices going around counterclockwise when you count from 1 to 3; when d = 3, P could be a tetrahedron where, if you position your right hand in its center and point your thumb at the 1-vertex, your fingers curl around in the same direction in which you count the remaining vertices from 2 to 4). Then any ordering of the vertices of any d-simplex in K may be said to have positive or negative orientation (chirality). (E.g. it would be positive when there's an orientation-preserving map (e.g. a rotation) sending each of its vertices to the correspondingly numbered vertices of P.)

So here's my extension of parent comment's theorem: Any coloring of the vertices of K with the colors {1, ..., d + 1} will contain an equal number of positively and negatively oriented chromatic d-simplices—that is, the reason the number of chromatic d-simplices in K must be even is that each one can be paired off with one of the opposite (mirror) orientation. (Does this theorem have a name? If so I couldn't find it.)

Following parent comment, the proof is by induction on the dimension d. When d = 1, K is just a cycle graph with vertices colored 1 or 2. As we go around clockwise (or counterclockwise), we must traverse an equal number of 1→2 edges and 2→1 edges (i.e. oppositely oriented 1-simplices), by the time we return to our starting point.

Now let d > 1, and assume the theorem is true in the (d-1)-dimensional case. As in parent comment, we may choose any vertex v of K, and then the faces opposite to v in each d-simplex in K that contains v will, together, form a (d-1)-dimensional subcomplex K′ of K that is homeomorphic (topologically equivalent) to a (d-1)-sphere.

Suppose v has color i. We will show that changing v's color to j ≠ i will add or remove the same number of positively oriented chromatic d-simplices as negatively oriented ones: Forget, for the moment, the distinction between colors i and j—say any i or j-colored vertex of K′ has color "i-or-j." Then K′ is now d-colored, so, by inductive hypothesis, the chromatic (d-1)-simplices of K′ must occur in pairs of opposite orientation (if any exist—if none exist, v can't be part of any chromatic d-simplex regardless of its color). Consider such a pair, call them F₁ and F₂.

Now cease pretending that i and j are a single color. Since F₁ was chromatic in K′, it must have had an i-or-j–colored vertex. Suppose, WOLOG, that that vertex was actually j-colored. Then, together with i-colored v, F₁ spans a chromatic d-simplex of K, call it S₁, which we may assume WOLOG to be positively oriented. Once we change the color of v from i to j, however, S₁ will have two j-colored vertices, and so will no longer be chromatic. To see that balance is maintained, consider what happens with F₂:

If F₂'s i-or-j–colored vertex was, like F₁'s, actually j-colored, then the d-simplex spanned by F₂ and v, call it S₂, was chromatic and negatively oriented (because F₂ had opposite orientation to F₁ in K′), and thus S₂ also ceased to be chromatic when we changed v's color from i to j, balancing S₁'s loss of chromatic status. Otherwise, F₂'s i-or-j–colored vertex must have been i-colored, in which case S₂ wasn't chromatic when v was also i-colored, but changing v's color to j turned S₂ into a new d-chromatic simplex. But what is S₂'s orientation? Well, it was negative under the assumption that S₂'s i-or-j–colored vertex was j-colored and v was i-colored, and swapping the labels of a pair of vertices in an oriented simplex reverses its orientation, so, under the present assumption, S₂'s orientation must be positive! Thus the loss of S₁ as a positively oriented chromatic d-simplex is balanced by the addition of S₂ as a new positively oriented chromatic d-simplex.

If all of K's vertices are the same color, it has the same number (zero) of positively and negatively oriented chromatic d-simplices, and since this parity is preserved when we change the colors of the vertices of K one at a time, it remains no matter how we (d+1)-color K. ☐

We can relate this theorem back to Sperner's lemma using the same trick as parent comment: Suppose we are given a triangulation K of a regular d-simplex S into smaller d-simplices, and a (d+1)-coloring of K's vertices that assigns a unique color to each vertex v of S, and doesn't use that color for any of K's vertices lying on the face of S opposite to v. We form a larger simplicial complex L containing K by adding d + 1 new vertices as follows: For i = 1, ..., d + 1, place a new i-colored vertex exterior to S, some distance from the center of S along the ray that goes through the i-colored vertex of S. Connect this new vertex to each vertex of K lying in the face of S opposite from the (i+1)-colored (or 1-colored, when i = d + 1) vertex of S. (Note that none of the d-simplices thereby created will be chromatic, because they won't have an (i+1)-colored vertex.) Then connect all of the new vertices to each other.

Having thus defined L, we can embed it in a d-sphere, of which it will constitute a triangulation, because the new vertices will form a d-simplex T whose "interior" is the complement of L in the sphere. Thus we can apply our above theorem to conclude that L has equally many positively and negatively oriented chromatic d-simplices. By construction, none of L's new vertices are included in any chromatic d-simplex other than T, so K must contain an equal number (possibly zero) of positively and negatively oriented chromatic d-simplices, plus one more, of opposite orientation to T. And what is the orientation of T? I claim that it is opposite to that of S: Consider T by itself, embedded in the sphere. T's boundary and exterior (the interior of L) then constitute another chromatic d-simplex, call it U, which is essentially just a magnification of S, with correspondingly colored vertices, and so share's S's orientation. Applying our theorem again, we see that T and U must have opposite orientations*, so we conclude that K must contain exactly one more chromatic d-simplex of the same orientation as S than of the opposite orientation. (As proved in nshepperd's comment for the case d = 2.)

*The observation, that, on the surface of a sphere, the interior and exterior of a trichromatic triangle have opposite orientations, is what sent me down this rabbit hole in the first place. :)

[-]Adele Lopez6yΩ220

Awesome! I was hoping that there would be a way to do this!

[-]Chris_Leong6yΩ4140

Some preliminary thoughts on q9:

As Jessicata pointed out, in 3-dimensions or higher, our n-hedra don't split up as nicely as in the 2d case.

That isn't the only issue: many of the surfaces of connected blocks may not correspond to the type of 2d grid that we just proved this result for and it doesn't seem trivial to figure out how to characterise what kind of grids we need to extend our result too (it will be even worse in higher dimensions)

I've found two results: firstly that if you remove a triangular face and replace it with three others (imagine allowing the surface to jut out of the page), then the trichromatic parity will be preserved. Secondly, that we can replace two triangle with four triangles

Given what I've discussed above, I'd be keen for a hint as learning enough geometry to make progress on this problem would seem to be taking me pretty far afield from maths useful for ai-risk.

[-]gjm6yΩ4140

Inappropriately highbrow proof of #4 (2d Sperner's lemma):

This proves a generalization: any number of dimensions, and any triangulation of the simplex in question. So, the setup is as follows. We have an n-dimensional simplex, defined by n+1 points in n-dimensional space. We colour the vertices with n+1 different colours. Then we triangulate it -- chop it up into smaller simplexes -- and we extend our colouring somehow in such a way that the vertices on any face (note: a face is the thing spanned by any subset of the vertices) of the big simplex are coloured using only the colours from the vertices that span that face. And the task is to prove that there are an odd number of little simplexes whose vertices have all n+1 colours.

This colouring defines a map from the vertices of the triangulation to the vertices of the big simplex: map each triangulation-vertex to the simplex-vertex that's the same colour. We can extend this map to the rest of each little simplex by linear interpolation. The resulting thing is continuous on the whole of the big simplex, so we have a continuous map (call it f) from the big simplex to itself. And we want to prove that we have an odd number of little simplices whose image under f spans the whole thing. (Call these "good" simplices.)

We'll do it with two ingredients. The easy one is induction: when proving this in n dimensions we shall assume we already proved it for smaller numbers of dimensions. The harder one is homology, a standard tool in algebraic topology. More precisely we'll do homology mod 2. It associates with each topological space X and each dimension d an abelian group Hd(X), and the key things you need to know are (1) that if you have f : X -> Y then you get an associated group homomorphism f* : Hd(X) -> Hd(Y), (2) that Hd(a simplex) is the cyclic group of order 2 if d=0, and the trivial group otherwise, and (3) that Hd(the boundary of a simplex) is the cyclic group of order 2 if d=0 or d = (dimension of simplex - 1) and the trivial group otherwise. Oh, and one other crucial thing: if you have f : X -> Y and g : Y -> Z then (gf)* = g*f*: composition of maps between topological space corresponds to composition of homomorphisms between their homology groups.

(You can do homology "over" any commutative ring. The groups you get are actually modules over that ring. It happens that the ring of integers mod 2 is what we want to use. A simplex is, topologically, the same thing as a ball, and its boundary the same thing as a sphere.)

OK. So, first of all suppose not only that the number of good simplices isn't odd, but that it's actually zero. Then f maps the whole of our simplex to its boundary. Let's also consider the rather boring map g from the boundary to the whole simplex that just leaves every point where it is. Now, if the thing we're trying to prove is true in lower dimensions then in particular the map gf -- start on the boundary of the simplex, stay where you are using g, and then map to the boundary of the simplex again using f -- has an image that, so to speak, covers each boundary face of the simplex an odd number of times. This guarantees -- sorry, I'm eliding some details here -- that (gf)* (from the cyclic group of order 2 to the cyclic group of order 2) doesn't map everything to the identity. But that's impossible, because (gf)*=g*f* and the map f* maps to Hn(whole simplex) which is the trivial group.

Unfortunately, what we actually need to assume in order to prove this thing by contradiction is something weaker: merely that the number of good simplices is even. We can basically do the same thing, because homology mod 2 "can't see" things that happen an even number of times, but to see that we need to look a bit further into how homology works. I'm not going to lay it all out here, but the idea is that to build the Hd(X) we begin with a space of things called "chains" which are like linear combinations (in this case over the field with two elements) of bits of X, we define a "boundary" operator which takes combinations of d-dimensional bits of X and turns them into combinations of (d-1)-dimensional bits in such a way that the boundary of the boundary of anything is always zero, and then we define Hd(x) as a quotient object: (d-dimensional things with zero boundary) / (boundaries of d+1-dimensional things). Then the way we go from f (a map of topological spaces) to f* (a homomorphism of homology groups) is that f extends in a natural way to a map between chains, and then it turns out that this map interacts with the boundary operator in the "right" way for this to yield a map between homology groups. And (getting, finally, to the point) if in our situation the number of good simplices is even, then this means that the map of chains corresponding to f sends anything in n dimensions to zero (essentially because it means that the interior of the simplex gets covered an even number of times and when working mod 2, even numbers are zero), which means that we can think of f* as mapping not to the homology groups of the whole simplex but to those of its boundary -- and then the argument above goes through the same as before.

I apologize for the handwaving above. (Specifically, the sentence beginning "This guarantees".) If you're familiar with this stuff, it will be apparent how to fill in the details. If not, trying to fill them in will only add to the pain of what's already too long a comment :-).

This is clearly much too much machinery to use here. I suspect that if we took the argument above, figured out exactly what bits of machinery it uses, and then optimized ruthlessly we might end up with a neat purely-combinatorial proof, but I regret that I am too lazy to try right now.

[-]Chris_Leong6yΩ4140

Rough approach for qu 6:

Join the center to each of the corners and color each segment a different color and arbitrarily coloring each ambiguous point. Radially extend the colored sections to infinity.

To prove f(x) has a fixed point consider g(x) = f(x) - x which can take values outside of the triangle. To find a fixed point, we simply need to show that g(x) will map at least one point to the center. It is easy to prove that each corner will map to the color opposite and each edge can only map to points of a different color (unless it passes through the center, in which case we would have obtained out proof). At this point the problem reduces to 5 assuming that we construct a big enough circle.

[-]riceissa6yΩ5140

My solution for #3:

Define $g : [0, 1] \to R$ by $g (x) = f (x) - x$ . We know that $g$ is continuous because $f$ and the identity map both are, and by the limit laws. Applying the intermediate value theorem (problem #2) we see that there exists $x \in [0, 1]$ such that $g (x) = 0$ . But this means $f (x) = x$ , so we are done.

Counterexample for the open interval: consider $f : (0, 1) \to (0, 1)$ defined by $f (x) = x / 2$ . First, we can verify that if $0 < x < 1$ then $0 < x / 2 < 1 / 2 < 1$ , so $f$ indeed maps to $(0, 1)$ . To see that there is no fixed point, note that the only solution to $x / 2 = x$ in $R$ is $0$ , which is not in $(0, 1)$ . (We can also view this graphically by plotting both $y = x$ and $y = x / 2$ and checking that they do not intersect in $(0, 1)$ .)

[-]Chris_Leong6yΩ3120

EDIT: I've got another framing that I thought would be more useful for later problems, but I was wrong. I still think there is some value in understanding this proof as well.

In particular, look at this diagram on Wikipedia. It would be better if the whole upper triangle was blue and the whole lower triangle were red instead of just one side (you can arbitrarily decide whether to paint the rest of the diagonal blue or red). If x=0 and x=1 aren't fixed points, then they must be blue and red respectively. If we split [0,1] into n components of size 1/n, then we can see where f(x) maps each such component to and form a line of colored points as in q1. Proving this using Sperner's Lemma is then essentially the same as qu2.

[-]Charlie Steiner6yΩ3110

Yeah, I did the same thing :)

Putting it right after #2 was highly suggestive - I wonder if this means there's some very different route I would have thought of instead, absent the framing.

[-]Rafael Harth6yΩ4130

I'm late, but I'm quite proud of this proof for #4:

Call the large triangle a graph and the $n^{2}$ triangles simply triangles. First, note that for any size, there is a graph where the top node is colored red, the remaining nodes on the right diagonal are colored green, and all nodes not on the right diagonal are colored blue. This graph meets the conditions, and has exactly one trichromatic triangle, namely the one at the top (no other triangle contains a red node). It is trivial to see that this graph can be changed into an arbitrary graph by re-coloring finitely many nodes. This will affect up to six triangles; we say that a triangle has changed iff it was trichromatic before the recoloring but not after, or vice versa, and we shall show that re-coloring any node leads to an even number of triangles being changed. This proves that the number of trichromatic triangles never stops being odd.

Label the three colors $x, y$ , and $z$ . Let $v$ be the node being recolored, wlog from $x$ to $y$ . Suppose first that $v$ has six neighbors. It is easy to see that a triangle between $v$ and two neighbors has changed if and only if one of the neighbors has color $z$ and the other has color $x$ or $y$ . Thus, we must show that the number of such triangles is even. If all neighbors have color $z$ , or if none of them do, then no triangles have changed. If exactly one node has color $z$ , then the two adjacent triangles have changed. Otherwise, let $j$ and $k$ denote two different neighbors of color $z$ . There are two paths using only neighbors of $v$ between $j$ and $k$ . Both start and end at a node of color $z$ . By the 1-D Sperner Lemma (assuming the more general result), it follows that both paths have an even number of edges between nodes of color $z$ and ${x, y}$ ; these correspond to the triangles that have changed.

If $v$ is a node on one of the graph's boundaries changing color from $x$ to $y$ , it has exactly 4 neighbors and three adjacent triangles. The two neighbors that are also on the boundary cannot have color $z$ , so either none, one, or both of the ones that aren't do. If it's none, no triangle has changed; if it's one, the two neighboring triangles have changed; and if it's both, then the two triangles with two nodes on the graph's boundary have changed.

[-]Chris_Leong6yΩ3120

Here's the rough idea for 5 (not a full-proof)

The bottom edge must stick in the blue and green sections meaning that if we were to divide the edge in n and see where these points map to, we would find that it would be blue or green and similarly the other edges would match the limitations in q4. If we look at the right corner, we see that the bottom edge maps to green or blue and the right edge maps to green or red, so the bottom corner must be in green. Similarly the other corners match the requirements of q4.

This lets us find a smaller trichromatic triangle. We can repeat this process an arbitrary number of times. Consider the range of possible x and y co-ordinates of elements in these triangles. Each time this will reduce by a particular factor, so we can see that the range of each co-ordinate will approach 0. I'll leave it to the reader to show that this means that these ranges converge to a point. I'll also leave it to the reader to show that each trichromatic sub-triangle must contain the center (you may want to look up winding numbers).

[-]Hoagy6yΩ3110

I've realised that you've gotta be careful with this method because when you find a trichromatic subtriangle of the original, it won't necessarily have the property of only having points of two colours along the edges, and so may not in fact contain a point that maps to the centre.

This isn't a problem if we just increase the number n by which we divide the whole triangle instead of recursively dividing subtriangles. Unfortunately now we're not reducing the range of co-ords where this fixed point must be, only finding a triad of arbitrarily close points that map to a triangle surrounding the centre. You can, for example, take the centre point of the first of these triangles (with some method of numbering to make the function definite) for each value of $n = 1, 2, 3..$ as a sequence in $R^{2}$ . This must have a convergent sequence which should converge to a point that maps to the centre but I can't prove that last stage.

[-]Chris_Leong6yΩ360

Yeah, you're right. That breaks the proof. I don't know how to deal with it yet.

[-]Chris_Leong6yΩ3120

Here's a solution to 4:

We will first prove a lemma that all connected groups of green blocks that are completely surrounded by red or blue blocks will produce an even number of trichromatic triangles. We will then augment the triangle by adding an extra blue row on the bottom and an extra red side on the right such that we now have would what be a triangle if it weren't missing the bottom right corner. This will mean that all green blocks will now be surrounded so we'll have an even number of trichromatic triangles, but we have added exactly one additional such triangle, so that the original has an odd number.

------

Proof of Lemma:

A trivial variant of 1-d Sperner's Lemma is that if we start and finish on the same colour, we get an even number of bichromatic edges. For any block that is completely surrounded by red and blue blocks, we apply this variant to show that there is an even number of bichromatic edges on the outside that then translates to an even number of trichromatic triangles.

EDIT: Actually, there is one case we can run into which is tricky and that is something like:

R R R R R

R G G G R

R G R B R

R G G G R

R R R R R R

To see how to solve this case, read how to solve tricky interior cases below.

END EDIT

Thick interior blocks work similarly, but we can run into weird scenarios such as a blue and a red surrounding by green block:

g g g

g b r g

g g g

We might also run into something like this (ie. a three-spoked shape that is blue at the center and red on the sides surrounded by green).

g g g

g r g g

g b r g

g r g g

g g g

For these weird shapes we can still trace a path around this interior section, we just include going both down and up a spoke in our path (thanks Hoagy!). So the interior sections are also even.

[-]TheWakalix6yΩ3110

Strategies that I've found helpful:

If something doesn't seem tractable, try flipping between algebraic and geometric interpretations of a problem. Problems 1 and 3 fell to this approach.

Specific solutions (or suggestive handwaving):

Problem 1:

I thought of it like parity - going left to right, each unichromatic edge doesn't change the color, while each bichromatic edge does. So to have an overall change, we need either 1 bichromatic edge, or 3 (1 and 2 that cancel), or 5 (1 and 4 that cancel)...

Problem 2:

I couldn't understand this one at first. After checking Wikipedia, I think that $R_{n}$ refers to the space that each point in the sequence lies within. An example of a finite sequence in $R_{2}$ would then be $(1, 2), (3, 1), (5, 3)$

Problem 3:

Consider the unit square. We need to draw one continuous line, going from left to right, that covers the entire vertical extent of the square. No matter how you do that, you need to cross the diagonal line from the bottom left to the top right.

Why? Because you need to touch the top and the bottom edges. You can't do that at the bottom-left or top-right corners, since then you'd touch the diagonal line. But then the point where you touch the top edge is entirely within the top triangle, and it cannot touch the bottom edge without entering the bottom triangle. Switching between triangles is identical to crossing the diagonal line.

As for why this isn't true if the set is open rather than closed: if we exclude the edges from our consideration of "does it intersect the diagonal", then it's fairly trivial to construct a curve that stays inside one triangle and has a codomain of (0,1). $f (x) = x^{2}$ should work.

[-]Charlie Steiner6yΩ3110

#8 actually comes up in physics:

in the field of nonlinear dynamics (pretty picture, actual wikipedia). The fact that continuous changes in functions can lead to surprising changes in fixed points (specifically stable attractors) is pretty darn important to understanding e.g. phase transitions!

[-]Charlie Steiner6yΩ3110

Does this work for #7? (and question) (Spoilers for #6):

I did #6 using 2D Sperner's lemma and closedeness. Imagine the the destination points are colored [as in #5, which was a nice hint] by where they are relative to their source points - split the possible difference vectors into a colored circle as in #5 [pick the center to be a fourth color so you can notice if you ever sample a fixed point directly, but if fixed points are rare this shouldn't matter], and take samples to make it look like 2d Sperner's lemma, in which there must be at least one interior tri-colored patch. Define a limit of zooming in that moves you towards the tri-colored patch, apply closedness to say the center (fixed) point is included, much like how we were encouraged to do #2 with 1D Sperner's lemma.

To do #7, it seems like you just need to show that there's a continuous bijection that preserves whether a point is interior or on the edge, from any convex compact subset of R^2 to any other. And there is indeed a recipe to do this - it's like you imagine sweeping a line across the two shapes, at rates such that they finish in equal time. Apply a 1D transformation (affine will do) at each point in time to make the two cross sections match up and there you are. This uses the property of convexity, even though it seems like you should be able to strengthen this theorem to work for simply connected compact subsets (if not - why not?).

EDIT: (It turns out that I think you can construct pathological shapes with uncountable numbers of edges for which a simple linear sweep fails no matter the angle, because you're not allowed to sweep over an edge of one shape while sweeping over a vertex of the other. But if we allow the angle to vary slightly with parametric 'time', I don't think there's any possible counterexample, because you can always find a way to start and end at a vertex.)

Then once you've mapped your subset to a triangle, you use #6. But.

This doesn't use the hint! And the hints have been so good and educational everywhere I've used them. So what am I missing about the hint?

[-]Gram Stone6yΩ2110

An attempt at problem #1; seems like there must be a shorter proof.

The proof idea is "If I flip a light switch an even number of times, then it must be in the same state that I found it in when I'm finished switching."

Theorem. Let $G = (V, E)$ e a path graph on $n$ ertices with a vertex $2$ oloring $c : V \mapsto {0, 1}$ uch that if $d e g (u) = d e g (v) = 1$ hen $c (u) \neq c (v)$ Let $S := {e \in E ∣ e$ s bichromatic $}$ Then $| S |$ s odd.

Proof. By the definition of a path graph, there exists a sequence ${⟨ v_{k} ⟩}_{1 < k \leq n}$ ndexing $V (G)$ An edge $e_{k} = {v_{k}, v_{k + 1}}$ s bichromatic iff $c (v_{k}) \neq c (v_{k + 1})$ A subgraph $H$ f $G$ s a state iff its terminal vertices are each incident with exactly one bichromatic edge or equal to a terminal vertex of $G$ The color of a state is the color of its vertices. There exists a subsequence of $⟨ v_{k} ⟩$ ontaining the least term of each state; the index of a state is equal to the index of its least term in this subsequence.

Note that none of the states with even indexes are the same color as any of the states with odd indexes; hence all of the states with even indexes are the same color, and all of the states with odd indexes are the same color.

For each state $H$ there exists a subsequence of $⟨ v_{k} ⟩$ orresponding to the vertices of $H$ and the least term of each subsequence is either $v_{1}$ r some $v_{k}$ hat is the greatest term in a bichromatic edge. Thus the number of states in $G = 1 + | S |$

By contradiction, suppose that $| S |$ s even. Then the number of states is odd, and the first and last states are the same color, so the terminal vertices of $G$ re the same color, contrary to our assumption that they are different colors. Thus $| S |$ ust be odd.

:::

[-]Gurkenglas6yΩ470

Turning each node but the last blue from left to right conserves the parity of the bichromatic edge count at each step until it is still odd at the end.

[-]Davidmanheim6yΩ3110

I'm stuck part-way through on #4 - I assume there is a way to do this without the exhaustive search I'm running into needing.

I'm going to try (nested) induction. Define triangles by side size, measured in nodes.

Induction base step: For n=2, there must be exactly one trichromatic edge.

Induction step: If there are an odd number of tri-chromatic edges for all triangles n=x, we must show that this implies the same for n=x+1.

We create all possible new triangles by adding x+1 nodes on one of the sides, then allow any of the previous x nodes on that side to change. Without loss of generality, assume we add x+1 edges to the bottom (non-red) side. These must be green or blue. The previous layer can now change any number of node-colors. We now must prove this by induction on color changes of nodes in the second-to-bottom layer to be red. (If they flip color otherwise, it is covered by a different base case.)

First, base step, assume no nodes change color. Because the previous triangle had an odd number of trichromatic edges, and the new edge is only green+blue, no new trichromatic edges were created.

Induction step: There is an x+1 triangle with an odd number of trichromatic vertices, and one node in the second-to-bottom layer changes to red. This can only create a new tri-cromatic triangle in one of the six adjacent triangles. We split this into (lots of) cases, and handle them one at a time.

(Now I get into WAY too many cases. I started and did most of the edge-node case, but it's a huge pain. Is there some other way to do this, presumably using some nifty graph theory I don't know, or will I need to list these out? Or should I not be using the nested induction step?)

Pointers welcome!

[-]Adele Lopez6yΩ4120

You can use 1d-Sperner to deal with all the cases effectively.

[-]Hoagy6yΩ4120

Here's a messy way that at least doesn't need too much exhaustive search:

First let's separate all of the red nodes into groups so that within each group you can get to any other node in that group only passing through red nodes, but not to red nodes in any other group.

Now, we trace out the paths that surround these groups - they immediately look like the paths from Question 1 so this feels like a good start. More precisely, we draw out the paths such that each vertex forms one side of a triangle that has a blue node at its opposite corner. Note that you can have multiple paths stemming from the same group if the group touches the side of the larger triangle, or if it has internal holes.

Now we have this set of paths we can split them into three kinds. The first is loops, which arise when you have a group which never touches the edge of the larger triangle, or inside 'holes' in large groups. These can be seen as a path starting and finishing at the same node. They therefore have an even number of b-g vertices. The second kind is those that begin at the edge of the large triangle and end at the same edge. These paths begin and end on the same colour and therefore also have an even number of b-g vertices. Finally and most importantly there is a kind of path that goes from one edge to the other -in the case of the reds, the left edge to the right edge. This will happen once with the group that includes the top red node, and if any other group spans the larger triangle then it will generate two more of these paths. Sperner's lemma tells us that these will have an odd number of b-g vertices and we know that there will be an odd number of such paths, so this final type generates an odd number of total b-g vertices.

By the way that we have defined these paths, the total number of r-g-b triangles is equal to the number of g-b vertices on the paths in the set generated above. This number is the sum of an odd number from the spanning paths and a series of even numbers from the other paths, giving an odd overall number of r-g-b vertices, proving number 4 (as long as I haven't made an error in categorizing the paths).

I hope this makes sense, let me know if it doesn't or has errors :)

[-]Davidmanheim6yΩ3110

I am having trouble figuring out why #2 needs / benefits from Sperner's Lemma.

But I keep going back to the proof that I'm comfortable with, which depends on connectedness, so I'm clearly missing an obvious alternative proof that doesn't need topology.

[-]Hoagy6yΩ6160

I was able to get at least (I think) close to proving 2 using Sperner's Lemma as follows:

You can map the continuous function f(x) to a path of the kind found in Question 1 of length n+1
by evaluating f(x) at x=0, x=1 and n-1 equally spaced divisions between these two points and setting a node as blue if f(x) < 0 else as green.

By Sperner's Lemma there is an odd, and therefore non-zero number of b-g vertices. You can then take any b-g pair of nodes as the starting points for a new path and repeat the process. After k iterations you have two values of x - only one where f(x) is below zero - that are 1/(n^k) away from each other. We thus can find arbitrarily close points that straddle zero. By taking the sequence f(x) of initial nodes x we get a sequence that, by B-W, has a sub-sequence which converges to zero. By continuity we have proved the existence of an x such that f(x)=0.

We can be sure that the sub-sequence does in fact converge to zero, rather than any other value because if it converges to any number |a|>0, the gradient of f(x) would have to be arbitrarily high to dip back below/above 0 for a value of x arbitrarily close by and therefore would not be a continuous function.

Comments to tighten up/poke holes in the above appreciated :)

[-]riceissa6yΩ3110

I'm having trouble understanding why we can't just fix $n = 2$ in your proof. Then at each iteration we bisect the interval, so we wouldn't be using the "full power" of the 1-D Sperner's lemma (we would just be using something close to the base case).

Also if we are only given that $f$ is continuous, does it make sense to talk about the gradient?

[-]Chris_Leong6yΩ4130

"I'm having trouble understanding why we can't just fix n=2 in your proof. Then at each iteration we bisect the interval, so we wouldn't be using the "full power" of the 1-D Sperner's lemma (we would just be using something close to the base case)." - You're right, you can prove this without using the full power of Sperner's lemma. I think it becomes more useful for the multi-dimensional case.

[-]Hoagy6yΩ3110

Yeah agreed, in fact I don't think you even need to continually bisect, you can just increase n indefinitely. Iterating becomes more dangerous as you move to higher dimensions because an n dimensional simplex with n+1 colours that has been coloured according to analogous rules doesn't necessarily contain the point that maps to zero.

On the second point, yes I'd been assuming that a bounded function had a bounded gradient, which certainly isn't true for say sin(x^2), the final step needs more work, I like the way you did it in the proof below.

[-]Czynski6yΩ230

I hit that stumbling block as well. I handwaved it by saying "continue iterating until you have $x_{(k, B)}$ and $x_{(k, G)}$ such that $f (x_{k, B}) < 0$ , $f (x_{k, G}) \geq 0$ , and f has no local maxima or local minima on the open interval $(x_{k, B}, x_{k, G})$ ", but that doesn't work for the Weierstrass function, which will (I believe) never meet that criterion.

[-]riceissa6yΩ4120

Here is my attempt, based on Hoagy's proof.

Let $n \geq 1$ be an integer. We are given that $f (0 / n) = f (0) \leq 0$ and $f (n / n) = f (1) \geq 0$ . Now consider the points $0 / n, 1 / n, \dots, (n - 1) / n, n / n$ in the interval $[0, 1]$ . By 1-D Sperner's lemma, there are an odd number of $j \in {0, \dots, n}$ such that $f (j / n) \geq 0$ and $f ((j - 1) / n) \leq 0$ (i.e. an odd number of "segments" that begin below zero and end up above zero). In particular, $0$ is an even number, so there must be at least one such number $j$ . Choose the smallest and call this number $j_{n}$ .

Now consider the sequence $(j_{n} / n)_{n = 1}^{\infty}$ . Since this sequence takes values in $[0, 1]$ , it is bounded, and by the Bolzano–Weierstrass theorem there must be some subsequence $(k_{n} / n)_{n = 1}^{\infty}$ that converges to some number $x \in [0, 1]$ .

Consider the sequences $(f ((k_{n} - 1) / n))_{n = 1}^{\infty}$ and $(f (k_{n} / n))_{n = 1}^{\infty}$ . We have $f ((k_{n} - 1) / n) \leq 0 \leq f (k_{n} / n)$ for each $n \geq 1$ . By the limit laws, $(k_{n} - 1) / n \to x$ as $n \to \infty$ . Since $f$ is continuous, we have $f ((k_{n} - 1) / n) \to f (x)$ and $f (k_{n} / n) \to f (x)$ as $n \to \infty$ . Thus $f (x) \leq 0$ and $f (x) \geq 0$ , showing that $f (x) = 0$ , as desired.

[-]Rafael Harth6yΩ3100

Ex 1

Let $V = {v_{0}, . . ., v_{n}}$ and $e_{k} := (v_{k - 1}, v_{k})$ . Given an edge $e$ , let $ϕ_{e}$ denote the map that maps the color of the left to that of the right node. Given a $k \in {1, . . ., n}$ , let $ϕ_{k} = ϕ_{e_{k}} \circ . . . \circ ϕ_{e_{1}}$ . Let $b$ denote the color blue and $g$ the color green. Let $c (k)$ be 1 if edge $e_{k}$ is bichromatic, and 0 otherwise. Then we need to show that $ϕ_{n} (b) = g ⟹ (\sum_{k = 1}^{n} c (k)) is odd$ . We'll show $(\sum_{k = 1}^{n} c (k)) is even ⟺ ϕ_{n} (b) = b$ , which is a striclty stronger statement than the contrapositive.

For $n = 1$ , the LHS is equivalent to $c (ϕ_{1}) = 1$ , and indeed $ϕ (e_{1}) (b)$ equals $g$ if $e_{1}$ is bichromatic, and $b$ otherwise. Now let $n > 1$ and let it be true for $n - 1$ . Suppose $\sum_{k = 1}^{n} c (k) is even$ . Then, if $c (e_{n}) = 1$ , that means $(\sum_{k = 1}^{n - 1} c (k)) is odd$ , so that $ϕ_{n} (b) = ϕ_{e_{n}} (ϕ_{n - 1} (b)) = ϕ_{e_{n}} (g) = b$ , and if $c (e_{n}) = 0$ , then $(\sum_{k = 1}^{n - 1} c (k)) is even$ , so that $ϕ_{n} (b) = ϕ_{e_{n}} (ϕ_{n - 1} (b)) = ϕ_{e_{n}} (b) = b$ . Now suppose $\sum_{k = 1}^{n} c (k) is odd$ . If $c (e_{n}) = 1$ , then $(\sum_{k = 1}^{n - 1} c (k)) is even$ , so that $ϕ_{n} (b) = ϕ_{e_{n}} (ϕ_{n - 1} (b)) = ϕ_{e_{n}} (b) = g$ , and if $c (e_{n}) = 0$ , then $(\sum_{k = 1}^{n - 1} c (k)) is odd$ , so that $ϕ_{n} (b) = ϕ_{e_{n}} (ϕ_{n - 1} (b)) = ϕ_{e_{n}} (g) = g$ . This proves the lemma by induction.

Ex 2

Ordinarily I'd proof by contradiction, using sequences, that $inf {x \in [0, 1] | f (x) > 0}$ can neither be greater nor smaller than 0. I didn't manage a short way to do it using the two lemmas, but here's a long way.

Set $x_{0} = 0$ . Given $n \in N_{+}$ , let $G_{n}$ be a path graph of $n + 1$ vertices ${v_{n, 0}, . . ., v_{n, n}}$ , where $v_{n, k} = \frac{k}{n}$ . If for any $n$ and $k$ we have $f (v_{n, k}) = 0$ , then we're done, so assume we don't. Define $c (v, v^{'})$ to be 1 if $f (v)$ and $f (v^{'})$ have s different sign, and 0 otherwise. Sperner's Lemma says that the number of edges $e$ with $c (e) = 1$ are odd; in particular, there's at least one. Let the first one be denoted $(v, w)$ , then set $x_{n} = max {v, x_{n - 1}}$ .

Now consider the sequence $(x_{n})_{n \in N}$ . It's bounded because $x_{k} \in [0, 1]$ . Using the Bolzano-Weierstrass theorem, let $(x_{n}^{'})_{n \in N} \mapsto x^{*}$ be a convergent subsequence. Since $f (x_{k}) > 0$ for all $k \in N_{+}$ , we have $f (x^{*}) \geq 0$ . On the other hand, if $f (x^{*}) > 0$ , then, using continuity of $f$ , we find a number $x^{'} > x^{*}$ such that $f (x^{*}, x^{'}) > 0$ . Choose $n$ and $k$ such that $v_{n, k} \in (x^{*}, x^{'})$ , then $c (v_{n, j}) = 0$ for all $j < k$ , so that $x_{n} \geq v_{n, k} > x^{*}$ and then $x_{ℓ} \geq x_{n}$ for all $ℓ \geq k$ , so that $x^{*} \geq x_{n} \geq v_{n, k} > x^{*}$ , a contradiction.

Ex 3

Given such a function $f$ , let $g : [0, 1] \mapsto [- 1, 1]$ be defined by $g (x) = f (x) - x$ . We have $g (0) = f (0) - 0 \geq 0 \geq f (1) - 1 = g (1)$ . If either inequality isn't strict, we're done. Otherwise, $g (0) > 0 > g (1)$ . Taking for granted that the intermediate value theorem generalizes to this case, find a root $x^{*}$ of $g$ , then $f (x^{*}) = f (x^{*}) - x^{*} + x^{*} = g (x^{*}) + x^{*} = x^{*}$ .

[-]TheWakalix6y20

On your Ex. 2:

Is there something I'm missing? It seems to me that $x_{n} = v$ for all $n > 1$ .

[-]Rafael Harth6y10

$(v, w)$ is defined just for one particular graph. It's the first edge in that graph such that $f (v) < 0 < f (w)$ . (So it could have been called $(v_{n}, w_{n})$ ). Then for the next graph, it's a different $v$ . Basically, $x_{1}$ looks at where the first graph skips over the zero mark, then picks the last vertex before that point, then $x_{2}$ looks at the next larger graph, and if that graph skips later, it updates to the last vertex before that point in that graph, etc. I think the reason I didn't add indices to $(v, w)$ was just that there ar ealready the $v$ with two indices, but I see how it can be confusing since having no index makes it sound like it's the same value all throughout.

[-]Rafael Harth6yΩ290

Ex 5 (fixed version)

Let $D$ denote the triangle. For each $n \in N$ , construct a 2-d simplex $S_{n}$ with $(n + 1)^{2}$ nodes in $D$ , where the color of a point corresponds to the place in the disk that $f$ carries that point to, then choose $x_{n}$ to be a point within a trichromatic triangle in the graph. Then $(x_{n})_{n \in N}$ is a bounded sequence having a limit point $x^{*}$ . Let $t$ be the center of the disc; suppose that $f (x^{*}) \neq t$ . Then there is at least one region of the disc that $f (x^{*})$ doesn't touch. Let $ϵ$ be the distance to the furthest side, that is, let $ϵ = max {d (f (x^{*}), G), d (f (x^{*}), R), d (f (x^{*}), B)}$ . Since the sides are closed regions, we have $ϵ > 0$ . Using continuity of $f$ , choose $δ \in R_{+}$ small enough such that $B_{d} (x^{*}, δ) \subset B_{d} (f (x^{*}), ϵ)$ . Then choose $n \in N$ large enough so that (1) all triangles in $S_{n}$ have diameter less than $\frac{δ}{2}$ and (2) $d (x_{n}, x^{*}) < \frac{δ}{2}$ . Then, given any other point $y$ in the triangle around $x_{n}$ in $S_{n}$ , we have that $d (y, x^{*}) \leq d (y, x_{n}) + d (x_{n}, x^{*}) < \frac{δ}{2} + \frac{δ}{2} = δ$ , so that $d (f (y), f (x^{*})) < ϵ$ . This proves that the triangle in $S_{n}$ does not map points to all three sides of the disc, contradicting the fact that it is trichromatic.

Ex 6

(This is way easier to demonstrate in a picture in a way that leaves no doubt that it works than it is to write down, but I tried to do it anyway considering that to be part of the difficulty.)

(Assume the triangle $T = ¯ ¯¯¯¯¯¯¯¯¯¯ ¯ A B O$ is equilateral.) Imbed $T$ into $R^{2}$ such that $O = (0, 0)$ , $A = (- \frac{1}{2}, \frac{1}{2} \sqrt{3})$ , $B = (\frac{1}{2}, \frac{1}{2} \sqrt{3})$ . Let $f : T \mapsto T$ be continuous. Then $h : T \mapsto R^{2}$ given by $h : x \mapsto f (x) - x$ is also continuous. If $h (x) = O = (0, 0)$ then $(0, 0) = h (x) = f (x) - x ⟹ f (x) = x$ . Let $R$ be the circle with radius 2 around $O$ ; then $h (T) \subset R$ because $| | h (x) | | = | | f (x) - x | | \leq | | f (x) | | + | | x | | \leq 2$ (it is in fact contained in the circle with radius 1, but the size of the circle is inconsequential). We will use exercise 5 to show that $h$ maps a point to the center, which is $O$ , from which the desired result follows. For this, we shall show that it has the needed properties, with the modification that points on any side may map precisely into the center. It's obvious that weakening the requirement in this way preserves the result.

Rotate the disk so that the red shape is on top. In polar coordinates, the green area now contains all points with angles between $60^{\circ}$ and $180^{\circ}$ , the blue area contains those between $180^{\circ}$ and $300^{\circ}$ , and the red area those between $0^{\circ}$ and $60^{\circ}$ and those between $300^{\circ}$ and $360^{\circ}$ . We will show that $h (¯ ¯¯¯¯¯¯ ¯ A B)$ does not intersect the red area, except at the origin. First, note that we have

$h (¯ ¯¯¯¯¯¯ ¯ A B) = {f (x) - x | x \in ¯ ¯¯¯¯¯¯ ¯ A B} \subset {y - x | x \in ¯ ¯¯¯¯¯¯ ¯ A B, y \in T} = {T - x | x \in ¯ ¯¯¯¯¯¯ ¯ A B} = T - ¯ ¯¯¯¯¯¯ ¯ A B$

Since both $T$ and $¯ ¯¯¯¯¯¯ ¯ A B$ are convex combinations of finitely many points, it suffices to check all combinations that result by taking a corner from each. This means we need to check the points

$A - A$ and $B - A$ and $C - A$ and $A - B$ and $B - B$ and $C - B$ .

Which are easily computed to be

$(0, 0)$ and $(- 1, 0)$ and $(\frac{1}{2}, - \frac{1}{2} \sqrt{3})$ and $(1, 0)$ and $(0, 0)$ and $(- \frac{1}{2}, - \frac{1}{2} \sqrt{3})$

Two of those are precisely the origin, the other four have angles $270^{\circ}$ and $150^{\circ}$ and $90^{\circ}$ and $210^{\circ}$ . Indeed, they are all between $60^{\circ}$ and $300^{\circ}$ .

Now one needs to do the same for the sets $T - ¯ ¯¯¯¯¯¯ ¯ O A$ and $T - ¯ ¯¯¯¯¯¯ ¯ B O$ , but it goes through analogously.

[-]seed5y40

I am sorry because I cannot figure out how to hide big formulas in a spoiler. Also the spoiler feature is somewhat broken so it adds weird tabs around formulas.

#1:

Let's count the number of blue edge ends. Each blue point inside the segment is the end of two blue edges, and the leftmost blue vertex is the end of one. Therefore, their total number is odd. On the other hand, each bichromatic edge produces one blue edge end, and each unichromatic edge produces an odd number - zero or two - of blue edge ends. Therefore, an odd number of edges are bichromatic.

#2:

Suppose $x = inf {y \in [0, 1] | f (y) \geq 0}$ . If $f (x) > 0$ then $x \neq 0$ and, since f is continuous, f stays positive in some neighborhood of x, and then x is not the infimum. Therefore, f(x) = 0.

#3:

Consider the function $g (x) = f (x) - x$ . Since $g (0) \geq 0$ and $g (1) \leq 0$ by exercise 2, there should be a point where g(x) = 0.

#8.

Consider the family of functions: $f_{t} (x) = min (max (x - t + 0.5, 0), 1)$

For t < 0.5, the only fixed point is of $f_{t}$ is 1; for t > 0.5, the only fixed point is 0.

#9.

Lemma:

Suppose a k-dimensional simplex is subdivided into smaller k-dimensional simplices and all vertices are colored into k+1 colors so that there are no vertices of color i on the i-th edge of the big simplex. Then there are an odd number of subdivision simplices whose vertices are colored in k+1 different colors.

Proof:

Induction by k. Base k=1 proved in exercise 1.

Induction step: supposed the lemma is proved for k-1, let's prove it for k.

Let us count the number of tuples (X, Y) where X is a k-1-dimensional simplex colored in colors 0, 1, ..., k-1,

Y is a k-dimensional subdivision simplex, and X is on the boundary of Y. Each properly colored simplex X inside the big simplex produces two tuples, and each simplex on the boundary produces one tuple. X can only be on the k-th edge of the big simplex, and by the inductional assumption, there are an odd number of simplices X there. So, the total number of tuples is odd. On the other hand, each k-dimensional simplex Y can be a part of either:

0 tuples;

1 tuple if all his vertices are different;

2 tuples if has vertices of colors 0,1,...,k-1 but not all his vertices are different.

Therefore, a number of k-simplices Y with all different vertices must be odd.

Follows from 9

Suppose that center is not in the image of the triangle. Let us call a set of points bichromatic if it doesn't have points of all three colors. We color each point in the triangle in the same color as its image. Then every point in the image has an open bichromatic neighborhood. Since the map is continuous, the preimage of this neighborhood is also open. So, around every point in the triangle there can be drawn an open bichromatic ball of radius r. These balls are an open cover of the triangle, let us choose a finite subcover out of them. Suppose $ϵ$ s the minimum radius in this subcover. Split the triangle into subtriangles so that the diameter of each triangle is smaller than $ϵ / 2$ By Sperner's lemma, there is a trichromatic triangle, but since its diameter is smaller than $ϵ / 2$ it lies completely inside one of the bichromatic balls. Contradiction.

#10

First, I am going to prove that a function from a unit ball $D^{n}$ o itself has a fixed point, then that any compact convex subset of $R^{n}$ s homeomorphic to a ball.

Suppose that $f : D^{n} \to D^{n}$ as no fixed point, n>1 (case n=1 was proved in exercise 3). Then I can build a retraction from $D^{n}$ nto its boundary $S^{n - 1}$

send x to the first intersection of the ray (f(x), x) with $S^{n - 1}$ Let us prove that such a rectraction cannot exist. Suppose that such a rectraction $g$ exists. Denote $i : S^{n - 1} \to D^{n}$ the inclusion map. Then $g \circ i = i d$ nd the induced homology group homorphism $g^{*} \circ i^{*}$ ust also be identity: $H^{n - 1} (S^{n - 1}) \to^{i *} H^{n - 1} (D^{n}) \to^{g *} H^{n - 1} (S^{n - 1})$

But this is impossible because $H^{n - 1} (S^{n - 1}) = Z$ and $H^{n - 1} (D^{n}) = 0$

Now let us prove that any compact convex subset X of $R^{n}$ s homeomorphic to a ball. Let us select a maximum set of affinely independent points in X. They form some k-dimensional simplex, all X lies in the affine space spanned by this simplex, and all the interior of this simplex belongs to X, because X is convex. I'll take a ball $D^{k}$ f radius $d$ side this simplex and build a homeomorphism between X and $D^{k}$ . Taking the center of the ball as the center of coordinates, define

$f (x) = x * d / r (x))$ where $r (x) = r (| | x | |)$ s the distance to the farthest point of X in the $x$ direction, if $x \neq 0$ , 0 if

Let us prove that f and its inverse are continuous. Since X is compact, it is bounded, so there is a $R > 0$ such that $r (x) \leq R$ It follows that f and its inverse $f^{- 1} (x) = x * r (x) / d$ are continuous in zero: $\forall ϵ > 0$ if $| x | < R / d * ϵ$ $| f (x) | < ϵ$ $\forall ϵ > 0$ if $| x | < d / R * ϵ$ $| f^{- 1} (x) | < ϵ .$

Now let us prove that functions are continuous in all other points. It is sufficient to prove that r(x) is the continuous on the unit sphere. (Since composition and product of continuous functions is continuous, division by bounded from below (by d) continuous function r is continuous, ||x|| is a continuous function).

Since X is convex, the tangent cone from any point of X to $D^{k}$ lies in X. So if we take a point at the distance $R$ from the center, draw a tangent cone, and go down its boundary, we get the steepest possible rate of change of r(x) with respect to x. Therefore, r is continuous.

#6, #7: follow from #10.

#11:

Suppose f has no fixed point. Distance d(a, B) is a continuous function of a, and a continuous function reaches its minimum on a compact. TxT and the graph of f are nonitersecting compact sets, therefore the Hausdorff distance $δ$ between them is positive. It is easy to see that Hausdorff metric is indeed a metric, i.e. that a triangle inequality holds for it. So if we take any continuous function g at a distance less than $δ$ from f, its Hausdorff distance to TxT will be positive, so it can have no fixed points.

#13:

Suppose $h : S \to 2^{S}$ is a Kakutani function. We already know that any compact convex subset of $R^{n}$ s homeomorphic to a simplex. Denote $g : T \to S$ he homeomorphism between a simplex T and S.

Denote $y_{1}^{k}, \dots, y_{t}^{k}$ the k-th barithentric subdivision of T. For each $y_{i}^{k},$ choose an element $h_{i}^{k} \in h (g (y_{i}^{k}))$

Define $f_{k} (x)$ $\sum_{i = 1}^{n + 1} p_{i}^{k} (g^{- 1} (x)) h_{i}^{k}$ where $p_{i}^{k}$ are the baricentric coordinates of point $g^{- 1} (x)$ n its subdivision simplex. Function $f_{k}$ s continuous, $f_{k} (g (y_{i}^{k})) = h_{i}^{k}$ and, since S is convex, the image of $f_{k}$ lies in S.

By the Brouwer fixed point theorem, $f_{k}$ as a fixed point. Since S is compact, from the infinite sequence of fixed points of $f_{k}$ e can choose a convergent subsequence.

Suppose $x_{k} \to x^{*}$ s this subsequence, $g^{- 1} (x_{k})$ lies in the simplex $y_{1}^{k}, \dots, y_{n + 1}^{k}$ and has baricentric coordinates $p_{1}^{k}, \dots, p_{n + 1}^{k}$ . Then $g^{- 1} (x_{k}) = \sum p_{i}^{k} y_{i}^{k}$ and $f_{k} (x_{k}) = \sum p_{i}^{k} h_{i}^{k}$ so

$g^{- 1} (\sum p_{i}^{k} h_{i}^{k}) = \sum p_{i}^{k} y_{i}^{k}$ (1).

Since simplices go down in diameter, $g (y_{i}^{k}) \to x^{*}$ as $x_{k} \to x^{*}$ Each $p_{i}^{k} \in [0, 1]$ s a bounded sequence, so we can, sequentially, choose a convergent subsequence out of each of them, so we can assume that $p_{i}^{k} \to p_{i}^{*}$ Similarly, we can choose a convergent subsequence out of $h_{i}^{k}$ so we assume $h_{i}^{k} \to h_{i}^{*}$ The sequence $(g (y_{i}^{k}), h_{i}^{k})$ belongs to the graph of h and converges to the point $(x^{*}, h_{i}^{*})$ Since the graph is closed, $h_{i}^{*}$ must belong to the image of $x^{*}$ Since $\sum p_{i}^{k} = 1$ for every k, $\sum p_{i}^{*} = 1.$ ince the image is convex, $\sum p_{i}^{*} h_{i}^{*}$ lso belongs to the image of $x^{*}$ On the other hand, as we remember, since equality (1) held for every k, it also holds in the limit: $g^{- 1} (\sum p_{i}^{*} h_{i}^{*}) = \sum p_{i}^{*} g^{- 1} (x^{*})$ . Hence, $\sum p_{i}^{*} h_{i}^{*} = x^{*}$ So, $x^{*}$ is the fixed point of h.

[-]Ben Pace5y20

I just tried to fix all the things in your comment. You're right, weird stuff was happening :-)

[-]seed5y10

Thank you!

[-]Rafael Harth4y*20

Ex12

I didn't use the hint, so my solution looks different. I also don't get how the intended solution works -- you can't choose the cubes in small enough to make sure that $f$ is constant on each cube $C$ , so $f (C)$ may not be convex. This seems to kill the straight-line solution, and I didn't see a way to salvage it.

Here's what I did in one paragraph. Divide both $S$ and $T$ into cubes. For any horizontal edge $e$ in $S$ , make sure $f_{n}$ hits the centers of all cubes that $f$ touches on points within distance $ϵ$ of $e$ (where $ϵ$ is at least the diameter of a cube in $S$ ), while moving around only within those cubes. Extend $f_{n}$ to $S$ without wandering off too far, and voilà.

Proof roadmap:

Embed $S$ and $T$ into unit cubes
Cut the unit cubes into small cubes
Prove a bunch of helpful Lemmas
Define $f_{n}$ on some subset of the unit cube containing $S$
Argue that this approximates $f$ on $S$

(1) Since $S$ and $T$ are compact and hence bounded, we can scale them down such that we can consider them subspaces of the unit cubes, i.e., $S \subseteq X := [0, 1]^{d}$ and $T \subseteq Y := [0, 1]^{m}$ , where we choose $d, m$ as small as possible. (This is the abbreviated version of working with embedding functions.)

Let $n \in N_{+}$ .

(2) By cutting each interval into $n$ pieces, i.e., $[0, \frac{1}{n}], [\frac{1}{n}, \frac{2}{n}], . . . [\frac{n - 1}{n}, 1]$ , we obtain $n^{d}$ small cubes in $X$ of the form

$[\frac{j_{1}}{n}, \frac{j_{1} + 1}{n}] \times \dots \times [\frac{j_{n}}{n}, \frac{j_{n} + 1}{n}]$

where $j_{1}, . . ., j_{n} \in {0, . . ., n - 1}$ . Enumerate these cubes as $Cubes (X) := {C_{1}, . . ., C_{n^{d}}}$ . An analogous construction for $Y$ yields $Cubes (Y) := {D_{1}, . . ., D_{n^{m}}}$ .

Given any set $Q \subseteq Y$ , we define the operator $Expand$ to 'expand' $Y$ to all the cubes that it touches, i.e.,

$Expand (Q) := {D \in Cubes (Y) | D \cap Q \neq \emptyset}$

(3) We do most work via paths. This requires a bunch of Lemmas.

Lemma 1. For any connected set $C \subseteq S$ , the set $f (C)$ is connected.

Proof. Let $f (C) = U ⊔ V$ be a separation into two closed sets. Suppose first there is a point $x \in C$ not entirely contained in $U$ or $V$ . Then, $U \cap f (x)$ and $V \cap f (x)$ is a separation of $f (x)$ , contradicting the fact that $f (x)$ is convex (and hence (path)-connected.) Thus, each $f (x)$ either lies entirely in $U$ or entirely in $V$ .

Since $U$ is closed, so is $(S \times U) \cap G_{f}$ and $π_{1} ((S \times U) \cap G_{f})$ (where $G_{f}$ is the graph of $f$ ), which is simply $f^{- 1} (U)$ . (The preimage function is well-defined for $U$ and $V$ due to the result from the previous paragraph, and the projection is closed because $S$ is compact.) Analogously, $f^{- 1} (V)$ is closed. Then, $C = (C \cap f^{- 1} (V)) ⊔ (C \cap f^{- 1} (U))$ is a separation of $C$ , implying that (because $C$ is connected), one of them is the empty set. Since $U, V \subseteq f (C)$ , this implies that $U = \emptyset$ or $V = \emptyset$ .

This is only needed to prove Lemma 2.

Lemma 2. For any connected set $C \subseteq S$ , the set $Z := Expand (f (C))$ is path-connected.

Proof. The set $Z$ consists of cubes in $Y$ . Consider the graph $G$ where all cubes in $Z$ are nodes, and there is an edge between two nodes iff the cubes share at least a point. If this graph were disconnected, then there would be a minimal distance between the sets of cubes corresponding to two disconnected parts of the graph. This yields a separation of $Z$ , which is also a separation of $f (C)$ , contradicting the previous lemma. (The distance can, in fact, be lower-bounded, but it suffices to use the fact that two closed disjoint sets in a metric space have non-zero distance.) Thus, $G$ is connected. This allows us to construct a path between the center points of two arbitrary cubes in $Z$ (since there is a corresponding path in $G$ and the straight-line connection between the centers of two cubes that share at least one vertex yields a continuous path). Now, given two points $p, p^{'}$ and two cubes $D, D^{'}$ such that $p \in D \subseteq Z$ and $p^{'} \in D^{'} \subseteq Z$ , we can construct a path from $p$ to $p^{'}$ via

$p \to center (D) \to center (D^{'}) \to p^{'} .$

Lemma 3. Given $k \in N_{+}$ and any path-connected space $Z$ , all functions from $[0, 1]^{k}$ to $Z$ are homotopic.

Proof. Let $ϕ : [0, 1]^{k} \to Z$ . Define a homotopy $Φ : [0, 1] \times [0, 1]^{k} \to Z$ by the rule $Φ (t, x_{1}, . . ., x_{k}) = Φ ((1 - t) x_{1}, . . ., (1 - t) x_{k})$ . Then, $Φ (0)$ is $ϕ$ , and $Φ (1)$ is a constant map, proving that $ϕ$ is null-homotopic. Since being homotopic is an equivalence relation (and any two constant maps are trivially homotopic in a path connected space), it follows that all maps $[0, 1]^{k} \to Z$ are homotopic to each other.

(4) Let $ϵ \in R_{+}$ be a parameter that depends on $n$ . We will specify how $ϵ$ is chosen in the last part of the proof. It will have the properties that it's at least as large as the diameter of a cube and that it converges to $0$ as $n$ grows.

Let $A \subset S$ be connected. We define two operators on $A$ . The first is the set of points in $Y$ that wish for $f_{n}$ to hit on points near it. We set

$Targets (A) := {center (D) | \exists x \in B (A, ϵ) : f (x) \cap D \neq \emptyset}$

where $B (A, ϵ) = {x \in X | d (x, A) < ϵ}$ . The second is a sufficiently small subspace of $Y$ that is guaranteed to contain all points that $f$ touches on $A$ . We set $Area (A) := Expand (Targets (A))$ . Note that this set is identical to $Expand (f (B (A, ϵ)))$ , which makes it path-connected by Lemma 2.

We now want to define a partial function $f_{n} : X \to Y$ . We begin by defining it on vertices, then generalize it to specific edges, then specific faces, and so on, until we define it on all cubes $C \in Cubes (X)$ that intersect $S$ .

A vertex $v$ is defined to be a point $v \in X$ of the form

$v = (\frac{j_{1}}{n}, \frac{j_{2}}{n}, . . ., \frac{j_{n}}{n})$

for some $j_{1}, . . ., j_{n} \in N$ . The set $Area (v)$ may be empty if $v$ is too far outside $S$ , in which case we leave $f_{n}$ undefined on $v$ . If it is not empty, choose $y \in Area (v)$ arbitrarily and set $f_{n} (v) := y$ .

We now turn to edges. However, we only consider 'horizontal' edges, that is, subspaces $e \subset X$ of the form

$e = {(a, \frac{j_{2}}{n}, . . ., \frac{j_{n}}{n}) | a \in (\frac{j_{1}}{n}, \frac{j_{1} + 1}{n})}$

for some $j_{1}, . . ., j_{n} \in N$ . Let $v$ and $w$ be the two vertices of $e$ . If $f_{n}$ is undefined on either, we leave it undefined on $e$ . If not, we define it in the following. Note that this is the step where we guarantee that $f_{n}$ hits all points in the target set.

We know from Lemma 3 that there is a path $p : [0, 1] \to Area (e)$ from $f (v)$ to $f (w)$ . Since $e$ is homeomorphic to $[0, 1]$ , it's easy to transform $p$ into a 'path' $p^{'} : e \to Area (e)$ . But we can do even better and construct a path $p^{*} : e \to Area (e)$ that starts at $f_{n} (v)$ , ends at $f_{n} (w)$ , and hits all points in $Targets (e)$ on the way. (All trivial since $Area (e)$ is path-connected.) Now we simply set $f_{n} (x) = p^{*} (x) \forall x \in e$ .

We next consider all 'horizontal-vertical' faces, that is, all sets $q \subset X$ of the form

$q = {(a, b, \frac{j_{3}}{n}, . . ., \frac{j_{n}}{n}) | a \in (\frac{j_{1}}{n}, \frac{j_{1} + 1}{n}), b \in (\frac{j_{2}}{n}, \frac{j_{2} + 1}{n})}$

for some $j_{1}, . . ., j_{n} \in N$ . Let $e$ and $e^{'}$ be the two horizontal edges of $q$ . If $f_{n}$ is undefined on either, we leave it undefined on $q$ . If not, we have two paths $p : [0, 1] \to Area (q)$ and $p^{'} : [0, 1] \to Area (q)$ which implement $f_{n}$ on $e$ and $e^{'}$ , respectively. Using Lemma 3, we obtain a homotopy $F : [0, 1] \times [0, 1] \to Area (q)$ that continuously deforms $p$ into $p^{'}$ . Since our face $q$ is homeomorphic to $[0, 1] \times [0, 1]$ , it's easy to transform $F$ into a function $F^{*} : q \to Area (q)$ . Now we simply set $f_{n} (x) = F^{*} (x) \forall x \in q$ .

Now we do the same for 3-dimensional subspaces $r \subset X$ of the form

$r = {(a, b, c, \frac{j_{4}}{n}, . . ., \frac{j_{n}}{n}) | a \in (\frac{j_{1}}{n}, \frac{j_{1} + 1}{n}), b \in (\frac{j_{2}}{n}, \frac{j_{2} + 1}{n}), c \in (\frac{j_{3}}{n}, \frac{j_{3} + 1}{n})}$

where $f_{n}$ has been defined on the two horizontal-vertical faces, and so on. This way, every $k$ -dimensional subspace of this kind contains precisely two $k - 1$ -dimensional subspaces of this kind, and if we have defined $f_{n}$ on both, we can apply a construction analogous to the above to define $f_{n}$ on the $k$ -dimensional subspace. Eventually, we define $f_{n}$ on $d$ -dimensional subspaces, which are precisely our cubes. (In the case of $d$ -dimensional subspaces, the definition above doesn't pose any restriction; it coincides with the definition of a cube $C \in Cubes (X)$ ). Importantly, this defines $f_{n}$ on any cube $C \in Cubes (X)$ that intersects $S$ . (This is so because any vertex of this cube is within $ϵ$ of $S$ , which means that it has non-empty area. This implies that we have defined $f_{n}$ on any edge, face, and so on, of $C$ .) Thus, we end up having defined $f_{n}$ on some subspace of $X$ that includes all cubes that intersect $S$ .

The advantage of this construction is that, for any $C \in Cubes (X)$ , we know that $f (C)$ is contained in $Area (C)$ , which is the same as the union of all cubes in $Y$ that $f$ touches on points near $C$ . If we had used the homomorphic extension of $f_{n}$ instead (i.e., connecting via straight lines), we could merely guarantee that $f (C)$ is contained in the convex hull of certain points in $Y$ , which may be much larger.

(5) Having defined $f_{n}$ on a subset of $X$ that contains $S$ , we take a projection $π : Y \to T$ , and define $ϕ_{n} : S \to T$ by the rule $ϕ_{n} (x) = π (f_{n} (x))$ . It remains to show that our construction is such that the Hausdorff distance between $f$ and $f_{n}$ converges to 0 as $n \to \infty$ , then the distance between $f$ and $ϕ_{n}$ converges to $0$ as well. (To see this, note that, if $f_{n} (x)$ is within $δ$ of $f (x)$ (which lies in $S$ ), then $π$ can move it by at most $δ$ , which means that $π (f_{n} (x))$ is within $2 δ$ of $f (x)$ .)

To do this, we now explain how $ϵ$ is chosen, and then argue that the Hausdorff distance can be upper-bounded by some constant times $ϵ$ .

The issue we have to deal with is that, by default, a point on the boundary of $S$ may not have any edge close to it that is contained in $S$ . (In fact, it may not even have an edge close to it that intersects $S$ .) Thus, we would like $ϵ$ to be so large that any $ϵ$ -ball around a point in $S$ must contain a $δ$ -ball entirely contained in $S$ , where $δ$ is larger than the diameter of a cube. In that case, any $x \in S$ is within $ϵ$ of a cube entirely contained in $S$ and thus also within $ϵ$ of an edge entirely contained in $S$ .

It remains to show that we can choose $ϵ$ such that it (a) has this property and (b) converges to $0$ as a function of $n$ . To show this, we consider $ϵ \in R_{+}$ fixed, and show that $n$ eventually grows large enough for that $ϵ$ to suffice.

For every point $x \in S$ , there exists some $δ \in R_{+}$ such that $B (x, ϵ)$ contains some $δ$ -ball entirely contained in $S$ . Define a function $γ : S \to R_{+}$ that each point to the supremum of such $δ$ 's. Then, $γ$ is a continuous function from a compact set to $R_{+}$ , which means it takes on a minimum value. It now suffices to choose $n$ large enough that the diameter of a cube is smaller than this minimum. (To verify that $γ$ is continuous, take a sequence $(x_{n})_{n \in N}$ of points in $S$ , assuming that $(γ (x_{n}))_{n \in N}$ doesn't converge, and derive a contradiction.)

With this out the way, we return to the proof that $f$ is the Haudorff limit of the $f_{n}$ . This consists of showing two parts:

for any point on $G_{f}$ (the graph of $f$ ), there exists a close point on $G_{f_{n}}$ (i.e., $f_{n}$ comes sufficiently close to all points on $G_{f}$ ); and
for any point on $G_{f_{n}}$ , there exists a close point on $G_{f}$ (i.e., $f_{n}$ has no points too far away from $G_{f}$ ).

Both are now easy:

Let $(x, y) \in G_{f}$ , and let $D \in Cubes (Y)$ be a cube that contains $y$ . Let $e \subset S$ be an edge with distance at most $ϵ$ to $x$ . By construction, we have $center (D) \in Targets (e)$ , which means that there is a point $x^{'} \in e$ such that $y^{'} := f_{n} (x^{'}) = center (D)$ . Since $d (x, x^{'}) < ϵ$ and $d (y, y^{'}) < ϵ$ , the distance between $(x, y)$ and $(x^{'}, y^{'})$ converges to $0$ as $n \to \infty$ .
Let $(x^{'}, y^{'}) \in G_{f_{n}}$ , and let $D \in Cubes (Y)$ be a cube containing $y^{'}$ . Since $y^{'} \in D$ , it follows that $D \subset Area (x^{'})$ , which means there exists a point $x \in S$ such that $f (x) \cap D \neq \emptyset$ , which is to say, such that there is a $y \in D$ for which $(x, y) \in G_{f}$ . Now $d (x, x^{'}) < ϵ$ and $d (y, y^{'}) < ϵ$ , and thus the distance between $(x^{'}, y^{'})$ and $(x, y)$ again converges to $0$ as $n \to \infty$ .

Ex13

Follows from Ex11 and Ex12 :-)

[-]Rafael Harth5y20

Ex11

(I assume the graph of is compact; otherwise, the Hausdorff distance isn't defined, and there seem to be counter-examples to the claim of the exercise.)

Since each $f_{n}$ is a continuous function from $T$ to itself, it has a fixed point $x_{n}$ by Ex10. Then $(x_{n})_{n \in N}$ is a sequence of points in a compact space and thus has a limit point $x^{*}$ .

Let $G_{f}$ be the graph of $f$ . Assume for a contradiction that $x^{*} \notin f (x^{*})$ . Then, $(x^{*}, x^{*}) \notin G_{f}$ . Since $G_{f}$ is a compact subspace of the Hausdorff space $R^{n}$ , it is also closed. Let $O ⊊ T$ be an open set around $(x^{*}, x^{*})$ disjoint from $G_{f}$ . Then, we find an $ϵ \in R_{+}$ such that $B ((x^{*}, x^{*}), ϵ) \subseteq O$ . (This uses that $T$ is convex, otherwise the ball would exist in $R^{n}$ but could fall out of $T$ and hence $O$ .)

Choose $N \subseteq N$ infinite such that $(x_{n})_{n \in N}$ is entirely contained in $B (x^{*}, \frac{ϵ}{2})$ . Note that $(x_{n}, x_{n}) \in G_{f_{n}}$ by construction. Write $D$ for the Hausdorff distance, then $D (G_{f}, G_{f_{n}}) \geq d (G_{f}, (x_{n}, x_{n})) \geq \frac{ϵ}{2} \forall n \in N$ . This contradicts the fact that $(D (G_{f}, G_{f_{n}}))_{n \in N} converges to ⟶ 0$ , hence $x^{*} \in f (x^{*})$ .

[-]Rafael Harth5y20

Ex10

Mathematically, one can describe these areas as follows:

The $d$ areas of the kind $C_{k} := {x \in R^{d} : \sum_{j = 1}^{d} x_{j} < 0 \land x_{j} \geq 0 \forall j \neq k}$
The area where all coordinates are non-negative, $C_{d + 1} := {x \in R^{d} : x_{j} \geq 0 \forall j}$

The first $d$ faces can be characterized by the condition that $x_{k} = 0$ . Then for a point $x$ in this face, we have $g (x)_{k} = f (x)_{k} - x_{k} = f (x)_{k} \geq 0$ , hence $g (x) \notin C_{k}$ .
The final face can be characterized by the condition that $\sum x_{j} = 1$ . Then for a point $x$ in this face, we have that $\sum g (x)_{j} = \sum f (x)_{j} - \sum x_{j} = \sum f (x)_{j} - 1 \leq 0$ , hence $g (x) \notin C_{d + 1}$ . (Unless $g (x) = O$ , in which case we're also happy.)

And for the origin, we have $g (O)_{j} = f (O)_{j} - O_{j} = f (O)_{j} \geq 0$ , so $g (O) \in C_{d + 1}$

[-]Rafael Harth5y20

Ex 9

I'm weak with high-dimensional stuff, so I wanted to translate the statement into one about graphs. We characterize graphs by the following property:

Property P: every -clique in the graph has an equal number of extensions to $(j + 1)$ -cliques. (I.e., an equal number of nodes not in the clique that are connected to every node in the clique.)

(A simplex we translate into a graph has property P: every vertex has an equal number of edges it's a part of, every edge an equal number of faces it's a part of, and so on. That is, except for the vertices/edges at the... well, edges of the triangulation. Those have already made problems in Ex4.)

We now prove by induction that, given any $k \in N$ and a graph with property P where the largest cliques are $k$ -cliques, and any coloring $c : V \to {1, . . ., k}$ , the graph has an even number of $k$ -chromatic cliques.

Base case is $k = 2$ . The only such graph with property P is the cycle graph $C_{n}$ . Lemma follows from Ex. 1. (We need that $n \geq 3$ here, but that's fine.)

Inductive step: suppose the claim is true for some $k \in N$ and we have a graph where the largest cliques are $k + 1$ cliques and some coloring $c : V \to {1, . . ., k + 1}$ . We prove the step by constructing $c$ starting with the trivial coloring $c^{'}$ where $c^{'} \equiv 1$ . This coloring has no $k + 1$ -chromatic cliques, so in particular, the number of such cliques is even. We can transform $c^{'}$ into $c$ by repeatedly recoloring nodes, as in Ex4 -- and as in Ex4, the claim follows if we can prove that any step changes the number of $k + 1$ -chromatic cliques by an even number.

Let $x \in V$ , and suppose we change the color of $x$ from $n$ to $m$ . Recoloring $x$ can only change the $k + 1$ -chromatic-ness of cliques which contain $x$ . Let $ω$ be such a clique. Then $ω$ changes its $k + 1$ -chromatic-ness iff (a) precisely one of the nodes in $ω - {x}$ has color $n$ or $m$ , and (b) the remaining $k - 1$ colors of nodes in $ω - {x}$ are the set ${1, . . ., k + 1} - {n, m}$ . In other words, let $(V^{'}, E^{'})$ be the subgraph consisting of the neighbors of $x$ plus edges and let $c^{-}$ be the coloring obtained by $c$ if we merge colors $m$ and $n$ into one, then the number of cliques that change their $k + 1$ -chromaticness in $(V, E)$ is equal to the number of $k$ -chromatic cliques in $(V^{'}, E^{'})$ .

It now follows from the inductive assumption that the number of such cliques is even. We verify that $(V^{'}, E^{'})$ has property P: let $ρ$ be a $j$ -clique in $(V^{'}, E^{'})$ . Then, the claim follows from the fact that there is a one-to-one correspondence between $j + 1$ cliques extending $ρ$ in $(V^{'}, E^{'})$ and $j + 2$ cliques extending $ρ \cup {x}$ in $(V, E)$ . Furthermore, $(V^{'}, E^{'})$ has at most $k$ -large cliques since every node was connected to $x$ and thus lost one degree.

Given this, one can start with a triangulation where precisely one simplex is $k$ -chromatic (this is pretty straight-forward) and then use the Lemma to repeatedly recolor vertices without changing the number of $k$ -chromatic simplexes. Except, again, for the simplexes at the edges of the triangulation, but those should work similarly... I hope.

[-]Rafael Harth5y*20

I've always meant to come back to these at some point.

Ex7

Compact subsets of the plane are bounded (cover such a set by an expanding sequence of open balls and apply compactness). This means we can view as a subset of not just $R^{2}$ but also the closed triangle $T \subset R^{2}$ , appropriately scaled. Let $π : T \to S$ be the projection (the exercise tells us that $π$ is continuous (compact subsets of Hausdorff spaces are closed) ). Then $f \circ π : T \to S$ is continuous and since $S \subseteq T$ , it has a fixed point $x^{*}$ according to Ex6. Since the image of $f \circ π$ is just $S$ , this fixed point must lie in $S$ , and since $f \circ π \equiv f$ on $S$ , it's the desired fixed point for $f$ .

[-]ToasterLightning1y10

I'm just working my way through these problems in sequence.

1 is not particularly difficult to solve

Let's imagine the base case: B-G. Obviously, there is 1 biochromatic edge. Adding either B or G to a biochromatic edge will turn it into B-B-G or B-G-G respectively, which means there is still 1 bichromatic edge.
If you add B to a B-B or G to a G-G it turns into B-B-B or G-G-G, which does not add or destroy any bichromatic edges.
The final case is adding G to B-B or B to G-G, which makes either B-G-B or G-B-G, adding two bichromatic edges. Since adding two to an odd number results in an odd number, and we begin with 1 bichromatic edge, we always have an odd number of edges.

For a formal proof, we'd have to prove the unspoken assumption that we can make any finite linear path made up of Blue/Green nodes where the start is a Blue node and the end is a Green node, by adding Blue/Green nodes in between a B-G path.

The proof is as follows: Besides the start and end nodes, every node has two connections. Thus, we can remove a node and connect its two adjacent nodes to each other in its place. Removing a node this way does not make it no longer a qualifying path under our definitions, and the removal of a node can be undone by adding it back in between the two nodes. Thus, since we can remove all the nodes until we're left with a single B-G path, we can add them back until we've reached the original path, while still ensuring that there is an odd number of bichromatic edges.

Moderation Log

Curated and popular this week