Thanks for the link, I hadn't noticed this paper! They show that when you choose one position to train the probes on, choosing the exact answer position (last token of the answer of multi-token) gives the strongest probe.

After reading the section I think they (unfortunately) do not train a probe to classify every token.^[1] Instead the probe is exclusively trained on exact-answer tokens. Thus I (a) expect their probe scores will not be particularly sparse, and (b) to get good performance you'll probably need to still identify the exact answer token at test time (while in my appendix C you don't need that).

This doesn't matter much for their use-case (get good accuracy), but especially (a) does matter a lot for my use-case (make the scores LLM-digestible).

Nonetheless this is a great reference, I'll edit it into the post, thanks a lot!

1. ^{^}

   For every sensible token position (first, exact answer, last etc.) they train & evaluate a probe on that position, but I don't see any (training or) evaluation of a single probe run on the whole prompt. They certainly don't worry about the probe being sparse (which makes sense, it doesn't matter at all for their use-case).

Thanks! Fixed

I like this project! One thing I particularly like about it is that it extracts information from the model without access to the dataset (well, if you ignore the SAE part -- presumably one could have done the same by finding the "known entity" direction with a probe?). It has been a long-time goal of mine to do interpretability (in the past that was extracting features) without risking extracting properties of the dataset used (in the past: clusters/statistics of the SAE training dataset).

I wonder if you could turn this into a thing we can do with interp that no one else can. Specifically, what would be the non-interp method of getting these pairs, and would it perform similarly? A method I could imagine would be "sample random first token a, make model predict second token b, possibly filter by perplexity/loss" or other ideas based on just looking at the logits.

Thanks for thinking about this, I think this is an important topic!

Inside the AI's chain-of-thought, each forward pass can generate many English tokens instead of one, allowing more information to pass through the bottleneck.

I wonder how one would do this; do you mean allow the model to output a distribution of tokens for each output position? (and then also read-in that distribution) I could imagine this being somewhere between normal CoT and latent (neuralese) CoT!

After the chain-of-thought ends, and the AI is giving its final answer, it generates only one English token at a time, to make each token higher quality. The architecture might still generate many tokens in one forward pass, but a simple filter repeatedly deletes everything except its first token from the context window.

If my interpretation of your idea above is correct then I imagine this part would look just like top-k / top-p generation like it is done currently, which seems sensible.

I'm only ~30% certain that I correctly understood your idea though so I'd love if you could clarify how this generating many tokens idea looks like!

This is great advice! I appreciate that you emphasised "solving problems that no one else can solve, no matter how toy they might be", even if the problems are not real-world problems. Proofs that "this interpretability method works" are valuable, even if they do not (yet) prove that the interpretability method will be useful in real-word tasks.

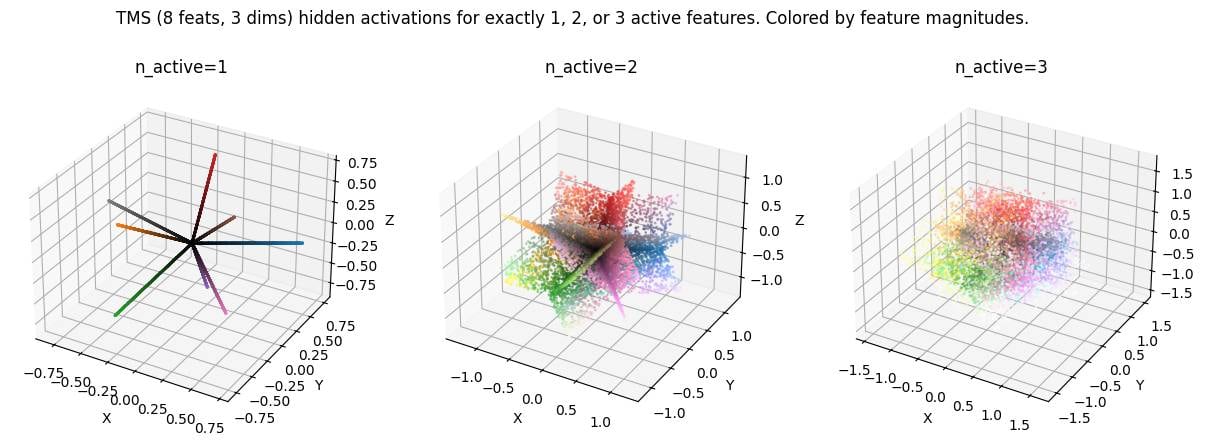
LLM activation space is spiky. This is not a novel idea but something I believe many mechanistic interpretability researchers are not aware of. Credit to Dmitry Vaintrob for making this idea clear to me, and to Dmitrii Krasheninnikov for inspiring this plot by showing me a similar plot in a setup with categorical features.

Under the superposition hypothesis, activations are linear combinations of a small number of features. This means there are discrete subspaces in activation space that are "allowed" (can be written as the sum of a small number of features), while the remaining space is "disallowed" (require much more than the typical number of features).^[1]

Here's a toy model (following TMS, $d_{vocab}=8$ total features in $d_{embed}=3$-dimensional activation space, with $k=1,2,3$ features allowed to be active simultaneously). Activation space is made up of discrete $k$-dimensional (intersecting) subspaces. My favourite image is the middle one ($k=2$) showing planes in 3d activation space because we expect $1\ll k\ll d_{embed}$ in realistic settings.

($n_{active}$ in the plot corresponds to $k$ here. Code here.)

This picture predicts that interpolating between two activations should take you out-of-distribution relatively quickly (up to possibly some error correction) unless your interpolation (steering) direction exactly corresponds to a feature. I think this is relevant because

1. it implies my stable region experiment series [we observe models are robust to perturbations of their activations, 1, 2, 3, 4] should be quite severely out-of-distribution, which makes me even more confused about our results.
2. it predicts activation steering to be severely out-of-distribution unless you pick a steering direction that is aligned with (a linear combination of) active feature directions.
3. it predicts that linear probing shouldn't give you nice continuous results: Probing into a feature direction should yield just interference noise most of the time (when the feature is inactive), and significant values only when the feature is active. Instead however, we typically observe non-negligible probe scores for most tokens.^[2]

we never substantially disrupt or change the deep-linking experience.

I largely retract my criticism based on this. I had thought it affected deep-links more than it does. ^[1]

Edit: I feel less strongly following the clarification below. habryka clarified that (a) they reverted a more disruptive version (pixel art deployed across the site) and (b) that ensuring minimal disruption on deep-links is a priority.

I'm not a fan of April Fools' events on LessWrong since it turned into the de-factor AI safety publication platform.

We want people to post serious research on the site, and many research results are solely hosted on LessWrong. For instance, this mech interp review has 22 references pointing to lesswrong.com (along with 22 further references to alignmentforum.org).

Imagine being a normal academic researcher following one of these references, and finding lesswrong.com on April Fools' day or Arkhipov / Petrov day^[1]. I expect there's a higher-than-normal chance you'll put this off as weird and not read the post (and possibly future references to LessWrong).

I would prefer LessWrong to not run these events (or make them opt-in), for the same reason I would expect arxiv.org not to do so.

Nice work, and well written up!

In reality, we observe that roughly 85% of recommendations stay the same when flipping nationality in the prompt and freezing reasoning traces. This suggests that the mechanism for the model deciding on its recommendation is mostly mediated through the reasoning trace, with a smaller less significant direct effect from the prompt to the recommendation.

The "reasoning" appears to end with a recommendation "The applicant may have difficulty making consistent loan payments" or "[the applicant is] likely to repay the loan on time", so I expect that re-generating the recommendation with frozen reasoning should almost never change the recommendation. (85% would seem low if all reasoning traces looked like this!) Actually the second paragraph seems to contain judging statements based on the nationality too.

I liked the follow-up test you run here, and if you're following up on this in the future I'd be excited to see a graph of "fraction of recommendations the same" vs "fraction of reasoning re-generated"!

I can see an argument for "outer alignment is also important, e.g. to avoid failure via sycophancy++", but this doesn't seem to disagree with this post? (I understand the post to argue what you should do about scheming, rather than whether scheming is the focus.)

Having good outer alignment incidentally prevents a lot of scheming. But the reverse isn't nearly as true.

I don't understand why this is true (I don't claim the reverse is true either). I don't expect a great deal of correlation / implication here.