If I say "the store is 500 meters away," is this strictly true? Strictly false? Either strictly true or strictly false, with probabilies of true or false summing to one? Fuzzily true, because the store is 500.1 meters away? My thesis is that it's strictly true or strictly false, with associated probabilities. Bear with me.
The 500 meter example is pretty hard to reason about numerically. I am hopeful that I can communicate my thoughts by starting with an example that is in some sense simpler.
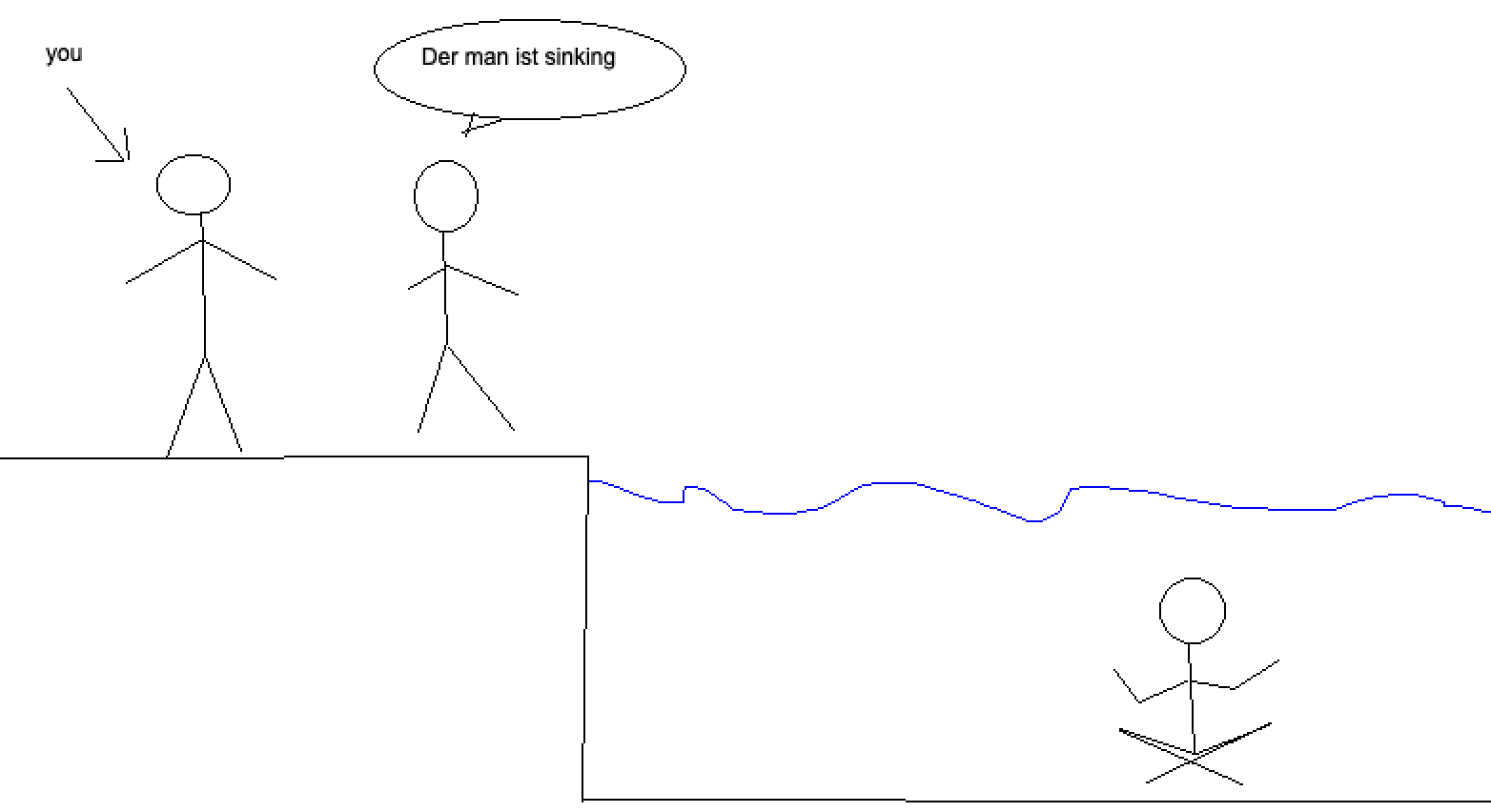
Is our conversational partner making a true statement or a false statement? What we're used to is starting with a prior over worlds, and then updating our belief based on observations- the man is underwater, the man is currently moving downwards. So our belief that the man is sinking should be pretty high.
However, what we are unsure of is the language of the sentence. If it's German¹, then it means¹ "the man is pensive." Then, evaluating the truth value of the sentence is going to involve a different prior- Does the man look deep in thought? He seems to have a calm expression, and is sitting cross legged, which is weak evidence. More consideration is needed.
To come out to an actual probability of the original sentence being true, we need a distribution of possible intended meanings for the sentence, and then likelyhoods of the truthfulness of each meaning. If you buy my framing of the situation, then in this case it's simply P(Sentence is English) x P(Man is sinking) + P(Sentence of is German) x P(Man is thoughtful).
In the monolingual case, it's easy to get caught up in lingual proscriptivism. If someone uses a word wrong, and their sentence is only true when it's interpreted using the incorrect definition, then a common claim is that their sentence is untrue. A classic example of this is "He's literally the best cook ever." I hope that the multilingual case illustrates that ambiguity in the meaning of phrases doesn't have to come from uncareful sentence construction or "wrong" word use.
I claim that there's just always a distribution over meanings, and it can be sharp or fuzzy or bimodal or any sort of shape. Of course, as a listener you can update this distribution based on evidence just like anything else. As a speaker, you can work to keep this distribution sharp as an aid to those you speak with, though total success is impossible.
To directly engage with the examples from the post: The statement "the store is 500 meters away" has a pretty broad and intractable distribution of meanings, but the case where
* The meaning was "The store is 500 meter away, to exact platonic accuracy"
* The store was actually a different distance, such as a value between 510.1 and 510.2 meters.
contributes only a vanishingly small amount to the odds that the statement was false.
Another case where
* The meaning was "The store is 500 meters away to a precision of 1 meter"
* The store is actually 503 meters away
contributes little to the odds that the statement was false, but contributes more if for example the speaker is holding a laser rangefinder. Odds of meanings update just like odds of world states.
For another example,
A: Is there any water in the refrigerator?
B: Yes.
A: Where? I don’t see it.
B: In the cells of the eggplant.
There is a real distribution of meanings for the statement "Yes." Our prior that A and B are effectively communicating starts low, but it is happy to rapidly increase if we recieve information like "A is deciding whether to store this calcium carbide in the refrigerator."
In my view, and assuming some sort of natural abstraction hypothesis, statements like "Every point on a sphere is equally distant from the center" are special because a significant part of their meaning is concentrated in little dirac deltas in meaning space. They are still allowed to be ambiguous or even fuzzy with some probability, but they also have a real chance of being precise.
¹ Admittedly broken German, with apologies. I possibly could come up with a better example, but I already had a great deal of time sunk into the illustration.
I would be surprised if grocery stores sold edge cases... But perhaps it was a farmer's market or something, perhaps a seller who often liked to sell weird things, perhaps grew hybridized plants. I'll take the case where it's a fresh vegetable/fruit/whatever thing that looks kind of eggplant-ish.
Anyway, that would generally be determined by: Why do I care whether he bought an eggplant? If I just want to make sure he has food, then that thing looks like it counts and that's good enough for me. If I was going to make a recipe that called for eggplant, and he was supposed to buy one for me, then I'd want to know if its flesh, its taste, etc., were similar enough to an eggplant to work with the recipe (and depending on how picky the target audience was). If I were studying plants for its own sake, I might want to interrogate him about its genetics (or the contact info of the seller if he didn't know). If I wanted to be able to tell someone else what it was, then... default description is "it's an edge case of an eggplant", and ideally I'd be able to call it a "half-eggplant, half-X" and know what X was; and how much I care about that information is determined by the context.
I think, in all of these cases, I would decide "Well, it's kind of an eggplant and kind of not", and lose interest in the question of whether I would call it an "eggplant" (except in that last case, though personally I'm with Feynman's dad on not caring too much about the official name of such things) in favor of the underlying question that I cared about. My initial idea, that there would be either a classical eggplant or nothing in the kitchen, turned out to be incoherent in the face of reality, and I dropped the idea in favor of some new approximation to reality that was true and was relevant to my purpose.
What do you know, there's an Eliezer essay on "dissolving the question". Though working through an example is done in another post (on the question "If a tree falls in a forest...?").