New Comment
A similar calibration game I like to play with my girlfriend: one of us gives our 80% confidence interval for some quantity (eg "how long will it take us to get to the front of this line?") and the other offers to bet on the inside or the outside, at 4:1 odds.
I've learned that my 80% intervals are right like 50% of the time, almost always in favor of being too optimistic...
We played this at an EA meet up and it was great fun!
I made a scoring card for this, feel free to use and share
https://drive.google.com/file/d/1LTM-AEfyEJSgqzxRrcJ6RamQ9-FUNtAk/view?usp=sharing
Jane Street hosts a very similar game called Estimathon (https://estimathon.com/how-to-play). The scoring rule is a bit different:
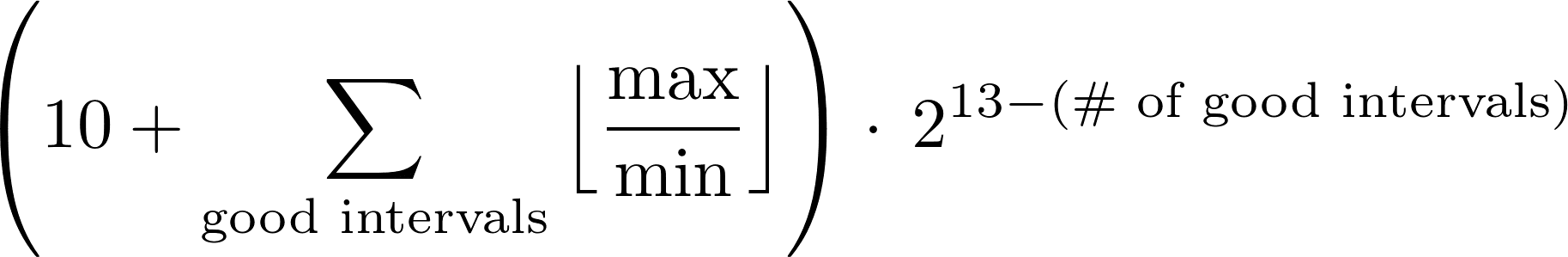
Published on LW with permission from Ben Orlin. Originally published in the book Math Games with Bad Drawings, which is includes many more fun math games, all thoughtfully wrote up like below. And also more silly doodles, which I have not reproduced here - get the book for the full experience!
Also see Breaking Rank, from the same book, and Calibration Trivia for instructions on how to run a meetup for a more hardcore calibration game.
An Uncertain Trivia Game For an Uncertain World
I enjoy trivia games: the camaraderie, the tension, the chips, the salsa... all of it, really, except the pesky part where I need to know things.
Outrangeous is a game for folks like me. You answer each question ("How many apostles did Jesus have?") not with a specific number, but with a range. Miss the truth (e.g., "50 to 100"), and you score no points (hence, "out-range-ous"). Capture the truth, and you score more points based on how narrow your range is (so "10 to 13" beats "11 to 18").
In the end, the game isn't about how much you know. It's about recognizing what you don't.
How to Play
What do you need?
Before beginning, have everybody take five minutes to come up with a few trivia questions whose answers are (a) numbers and (b) easily googled.
What's the goal?
Each answer is a number. You'll guess a range of values, trying to make it as narrow as possible while still including the true answer.
What are the rules?
Tasting Notes
Upon first formulating your guess, you'll feel pretty good. Then, when the answer is revealed, you'll be shocked how often you missed.
This creates an incentive to "go wide." You can often beat the wrong guessers, and thereby rack up points, merely by admitting your own ignorance.
Then again, if everyone is going wide, there's an incentive to go a bit narrower. In a world full of people guessing 0 to 1 million, the person guessing 5 to 500 is king. To explore this dynamic, let's focus on a simple question for two players.
We'll roll a 10-sided die. The question is "What number will come up?"
Now, if I guess a wide range, like 1 to 8, then your best bet is to undercut me with 1 to 7. That way, if the answer is 1, 2, 3, 4, 5, 6, or 7, then you win by virtue of your narrower range. Meanwhile, if the answer is 9 or 10, nobody is right, and it's a wash. You'll only lose if the die turns up an 8.
What if I guess a narrow range, like 1 to 3? In that case, your best move is to go as wide as possible: 1 to 10. You'll lose if the die comes up 1, 2, or 3, but you'll win if it comes up 4, 5, 6, 7, 8, 9, or 10. It's worth the trade-off (and better than going for the 1-to-2 undercut).
In short: If I go wide, you should go a little narrower, and if I go narrow, you should go wide.
For exactly this reason, I'd be a fool to tell you what range I'm going to pick. Instead, I'm going to randomize my answers. You'd be wise to do the same. With game theory, we can calculate the optimal probabilities:
Weird, right?
Your actual best strategy will vary depending on the question, the score, your own knowledge, and the number of players (the more there are, the wider you want to go). But I hope this gives a taste of the game's subtle pressures.
Where it Comes From
In Douglas Hubbard's How to Measure Anything, I came across 10 Outrangeous-style questions, along with an instruction: Make each range wide enough that you're 90% confident of capturing the true answer. That's 90% exactly: no more, no less. As a math teacher, a probability aficionado, and (as my siblings describe me) "a robot," I felt positive I'd nail it. I'd be 90% accurate, missing one of the 10. Maybe zero or two, depending on my luck.
Instead, I missed four.
Watching my surefire A- pale into a D- prompted a small crisis of confidence. As it should have, because my confidence was the whole problem. My confidence had slipped its leash and was now running amok, barking at squirrels, chasing traffic. How could I trust myself to calculate life's risks and rewards knowing I had such an inflated sense of my own powers?
Inspired and chastened, I developed Outrangeous[1] as a classroom game. Other folks have independently developed the same concept.
Why it Matters
Because to take calculated risks, you must know the limits of your own calculations.
Humans are not perfect. Your view of the world, just like mine, is a simmering mix of fact and fiction, history and myth, "tomato is a fruit" and "who am I kidding; you can't put tomato in a fruit salad." The question isn't whether my beliefs are true or false. I have true and false beliefs, both in abundance. The question is whether I can tell the two apart, and the sorry reality is most of us can't. We carry all of our opinions, right and wrong alike, with a swashbuckling, wholly unearned confidence.
In a classic study, psychologists Pauline Adams and Joe Adams quizzed subjects on how to spell some tricky words, and asked them to rate their confidence in each. Occasionally, folks would say "100%." That means deadlock certainty. Total guarantee. If I created a You Tube supercut of every time you've ever claimed 100% certainty, it should include exactly zero cases in which you were wrong.
Instead, on such 100% answers, the study found a 20% rate of error. "I'm absolutely positive and would bet my cat's life on it" translates to "Eh, call it four out of five."
A little overconfidence isn't a crime, at least not in most jurisdictions. It can even help, by giving us the courage to start an ambitious yet likely-to-fail project, such as writing a novel, running for political office, or reaching in-box zero. Still, whenever humans work together, we need to share our knowledge. That's a doomed endeavor if nobody can distinguish their knowledge from their ignorance. What's the point of pooling our money if we can't tell the real bills from the counterfeits?
Luckily, a noble few have learned to navigate these dark tunnels of uncertainty. They are called statisticians, and they will tell you, in no uncertain terms, that nothing is truly certain.
Imagine a study that finds the average American thinks about cheese 14.2 times per day. No matter how careful the researchers, or how tantalizing the Gruyere, there remains a modicum of doubt. Perhaps the true answer is a little lower (because we polled an unusually cheese-loving sample) or a little higher (because our subjects were unusually cheese-averse).
The solution is a confidence interval. Or better yet, a collection of them.
Such intervals embody an inherent trade-off. You can give a narrow, precise range. Or you can give a wide range that's almost certain to capture the truth. But you can't do both at once.
The tighter the range, the greater the risk of missing the mark.
Outrangeous demands the same trade-off. You can give a narrow range, which might garner a lot of points. Or you can give a wide range, upping your chances to score at least some points. You just can't do both at once.
To execute either strategy, you need to pursue a rarefied psychological state: good calibration. This means that your confidence matches your accuracy. When you feel 90% confident, you're right 90% of the time. When you feel 50% confident, you're right 50% of the time. You say what you mean and mean what you say. Subjective feeling aligns with objective success.
To be clear, good calibration is a narrow virtue. If you're 50% confident that sharks are fish (true) and 50% confident that prairie dogs are fish (not so much), then you're well calibrated, but a fool.
Meanwhile, if you're 5% confident that testing your bomb will extinguish life on earth, yet you shrug and start the countdown, then you may or may not be well calibrated, but you're definitely a monster.
Good calibration isn't sufficient for good judgment. But it may very well be necessary. Games like Outrangeous offer a unique window into your calibration and a training ground for improving it.
When my wife was in grad school for math, we'd team up with some friends from her program to play bar trivia on Thursday nights. Our team won every week, and usually in the same way: by hanging close in the themed rounds (sports, geography, music, etc.), then surging to victory in the final general knowledge round.
This posed a bit of a mystery. If another team outperformed us on, say, history, science, and film, then shouldn't they beat us on general knowledge, too?
I eventually developed a theory of our strange success. During themed rounds, a team can hand their answer sheet to the relevant specialist - the sports fan, the music expert, the geography whiz - and defer to them. But in general knowledge, no expert reigns. Everyone weighs in. You'll soon have four or five suggestions, one of them probably right. How do you know which? How can the group settle on the correct answer, rather than the most overconfident?
This is where the mathematicians shone. Mathematical research forces you to distinguish carefully between airtight knowledge, credible belief, plausible hunch, and blind guesswork. Our teammates never fought for an answer just because it was their own. Instead, the truth would rise to the top.
The mathematicians were well calibrated.
That's my belief, anyway. It's also possible that by the final round, everyone else was drunk, while the mathematicians held their liquor better. As with anything, I'll never be 100% sure.
Variations and Related Games
Ratio Scoring
Say we're guessing the distance to the moon. I put "3,000 miles to 300,000 miles," while you put "100,000 to 400,000 miles." We both get it right (the truth being 239,000). And, per the rules, my range is a bit narrower. But was mine really the better guess? My lower bound suggests that the moon and Earth might be closer together than New York and London. Your guess seems far more sensible. Shouldn't it score more highly?
The solution: divide rather than subtract. That is, calculate a ratio, rather than a width. Here, my ratio is 100 (that's 300,000 divided by 3,000), while yours is just 4 (from 400,000 divided by 100,000). Your guess is far more precise.
I recommend this scoring system for questions where ranges may span several orders of magnitude (e.g., "number of slot machines in Las Vegas"). For more restricted ranges (e.g., the age of a particular celebrity), the original scoring system works fine.
The Know-Nothing Trivia Game
Years ago, in the course of a long plane flight, the mathematician Jim Propp and two friends invented this strange jewel of a game. It's almost a contradiction in terms: a
trivia game you can play without ever finding out the answers.
It works for any odd number of players. Take turns coming up with a numerical trivia question (e.g., "How many home runs did Barry Bonds hit in his career?"); then all of you (including the question asker) write down a secret guess. When the guesses are revealed, the winner is whoever's guess is in the middle.
For example, if the three guesses are 900, 790, and 2,000, then the person who guessed 900 is the winner. Never mind that the truth is 762. You're not trying to guess the right answer, but the answer that will land between your friends' answers (though in practice that usually means just giving it your best guess).
Advice for Writing Questions
Spend 10 minutes on Google and/or Wikipedia before the game begins, so that by the time it's your turn to judge, you've got two or three questions ready to roll.
Play to your audience. Absurdly hard questions are no good; everyone just shrugs and gives a very wide range. The best questions are tantalizing: you don't know the answer, but feel like you should.
Phrase questions as precisely as possible. Where relevant, specify units ("distance in miles"), dates ("population as of 2019"), and sources ("the film's budget according to Wikipedia").
Here are some suggestions. You can also use these to inspire other ideas-just swap in a different celebrity/place/world record/piece of pop culture.
1 called it Humility at first, because that's what you need to win (and what my exuberant students often lacked). My friend Adam Bildersee later suggested the wittier Outrangeous.