Status: strong opinions, weakly held. not a control theorist; not only ready to eat my words, but I've already set the table.
As I understand it, the original good regulator theorem seems even dumber than you point out.
First, the original paper doesn't make sense to me. Not surprising, old papers are often like that, and I don't know any control theory... but here's John Baez also getting stuck, giving up, and deriving his own version of what he imagines the theorem should say:
when I tried to read Conant and Ashby’s paper, I got stuck. They use some very basic mathematical notation in nonstandard ways, and they don’t clearly state the hypotheses and conclusion of their theorem...
However, I have a guess about the essential core of Conant and Ashby’s theorem. So, I’ll state that, and then say more about their setup.
Needless to say, I looked around to see if someone else had already done the work of figuring out what Conant and Ashby were saying...
An unanswered StackExchange question asks whether anyone has a rigorous proof:
As pointed out by the authors of [3], the importance and generality of this theorem in control theory makes it comparable in importance to Einstein's for physics. However, as John C. Baez carefully argues in a blog post titled The Internal Model Principle it's not clear that Conant and Ashby's paper demonstrates what it sets out to prove. I'd like to add that many other researchers, besides myself, share John C. Baez' perspective.
Hello?? Isn't this one of the fundamental results of control theory? Where's a good proof of it? It's been cited 1,317 times and confidently brandished to make sweeping claims about how to e.g. organize society or make an ethical superintelligence.
It seems plausible that people just read the confident title (Every good regulator of a system must be a model of that system - of course the paper proves the claim in its title...), saw the citation count / assumed other people had checked it out (yay information cascades!), and figured it must be correct...
Motte and bailey
The paper starts off by introducing the components of the regulatory system:

OK, so we're going to be talking about how regulators which ensure good outcomes also model their environments, right? Sounds good.
Wait...

Later...

We're talking about the entire outcome space again. In the introduction we focused on regulators ensuring 'good' states, but we immediately gave that up to talk about entropy .
Why does this matter? Well...
The original theorem seems even dumber than John points out
John writes:
Also, though I don’t consider it a “problem” so much as a choice which I think most people here will find more familiar:
- The theorem uses entropy-minimization as its notion of optimality, rather than expected-utility-maximization
I suppose my intuition is that this is actually a significant problem.
At first glance, Good Regulator seems to basically prove something like 'there's a deterministic optimal policy wrt the observations', but even that's too generous - it proves that there's a deterministic way to minimize outcome entropy. But what does that guarantee us - how do we know that's a 'good regulator'? Like, imagine an environment with a strong "attractor" outcome, like the streets being full of garbage. The regulator can try to push against this, but they can't always succeed due to the influence of random latent variables (this cuts against the determinism assumption, but you note that this can be rectified by reincluding ). However, by sitting back, they can ensure that the streets are full of garbage.
The regulator does so, minimizes the entropy over the unconditional outcome distribution , and is christened a 'good regulator' which has built a 'model' of the environment. In reality, we have a deterministic regulator which does nothing, and our streets are full of trash.
Now, I think it's possible I've misunderstood, so I'd appreciate correction if I have. But if I haven't, and if no control theorists have in fact repaired and expanded this theorem before John's post...
If that's true, what the heck happened? Control theorists just left a $100 bill on the ground for decades? A quick !scholar search doesn't reveal any good critiques.
"Good regulator" is used here to mean that it is good at keeping the output "regular". That is, reducing the entropy instead of "a regulator which produces good".
On page 4 the authors acknowledge that there are numerous ways by which one could consider a regulator successful, then go on to say "In this paper we shall use the last measure, H(Z), and we define ‘successful regulation’ as equivalent, to ‘H(Z) is minimal’."
The fact that reducing entropy doesn't line up with maximizing utility is true, but the authors never claimed it did. Reducing entropy generalises to a lot of real world problems.
The reason I think entropy minimization is basically an ok choice here is that there's not much restriction on which variable's entropy is minimized. There's enough freedom that we can transform an expected-utility-maximization problem into an entropy-minimization problem.
In particular, suppose we have a utility variable U, and we want to maximize E[U]. As long as possible values of U are bounded above, we can subtract a constant without changing anything, making U strictly negative. Then, we define a new random variable Z, which is generated from U in such a way that its entropy (given U) is -U bits. For instance, we could let Z be a list of 50/50 coin flips, plus one biased coin flip with bias chosen so the entropy of the coin flip is , i.e. the fractional part of U. Then, minimizing entropy of Z (unconditional on U) is equivalent to maximizing E[U].
I had a little tinker with this. It's straightforward to choose a utility function where maximising it is equivalent to minimizing - just set .
As far as I can see, the other way round is basically as you suggested, but a tiny bit more fiddly. We can indeed produce a nonpositive from which we make a new RV with as you suggested (e.g. with coinflips etc). But a simple shift of isn't enough. We need (for some scalar and ) - note the term.
We take the outcomes to be partitioned by , i.e. they're ' happened and also I got coinflip outcome'. Then (where is understood to be the particular associated with ). That means so (you can check this by spelling things out pointfully and rearranging, but I realised that I was just rederiving conditional entropy laws).
Then
so minimizing is equivalent to maximising .
Requiring to be nonpositive for all maybe places more constraints on things? Certainly needs to be bounded above as you said. It's also a bit weird and embedded as you hinted, because this utility function depends on the probability of the outcome, which is the thing being controlled/regulated by the decisioner. I don't know if there are systems where this might not be well-defined even for bounded , haven't dug into it.
Okay, I agree that if you remove their determinism & full observability assumption (as you did in the post), it seems like your construction should work.
I still think that the original paper seems awful (because it's their responsibility to justify choices like this in order to explain how their result captures the intuitive meaning of a 'good regulator').
Oh absolutely, the original is still awful and their proof does not work with the construction I just gave.
BTW, this got a huge grin out of me:
Status: strong opinions, weakly held. not a control theorist; not only ready to eat my words, but I've already set the table.
As I understand it, the original good regulator theorem seems even dumber than you point out.
I'm really happy to see this. I've had similar thoughts about the Good Regulator Theorem, but didn't take the time to write them up or really pursue the fix.
Marginally related: my hope at some point was to fix the Good Regulator Theorem and then integrate it with other representation theorems, to come up with a representation theorem which derived several things simultaneously:
- Probabilistic beliefs (or some appropriate generalization).
- Expected utility theory (or some appropriate generalization).
- A notion of "truth" based on map/territory correspondence (or some appropriate modification). This is the Good Regulator part.
The most ambitious version I can think of would address several more questions:
A. Some justification for the basic algebra. (I think sigma-algebras are probably not the right algebra to base beliefs on. Something resembling linear logic might be better for reasons we've discussed privately; that's very speculative of course. Ideally the right algebra should be derived from considerations arising in construction of the representation theorem, rather than attempting to force any outcome top-down.) This is related to questions of what's the right logic, and should touch on questions of constructivism vs platonism. Due to point #3, it should also touch on formal theories of truth, particularly if we can manage a theorem related to embedded agency rather than cartesian (dualistic) agency.
B. It should be better than CCT in that it should represent the full preference ordering, rather than only the optimal policy. This may or may not lead to InfraBayesian beliefs /expected values (the InfraBayesian representation theorem being a generalization of CCT which represents the whole preference ordering).
C. It should ideally deal with logical uncertainty, not just the logically omniscient case. This is hard. (But your representation theorem for logical induction is a start.) Or failing that, it should at least deal with a logically omniscient version of Radical Probabilism, ie address the radical-probabilist critique of Bayesian updating. (See my post Radical Probabilism; currently typing on a phone, so getting links isn't convenient.
D. Obviously it would ideally also deal with questions of CDT vs EDT (ie present a solution to the problem of counterfactuals).
E. And deal with tiling problems, perhaps as part of the basic criteria.
I think sigma-algebras are probably not the right algebra to base beliefs on. Something resembling linear logic might be better for reasons we've discussed privately; that's very speculative of course. Ideally the right algebra should be derived from considerations arising in construction of the representation theorem, rather than attempting to force any outcome top-down.
Have you elaborated on this somewhere or can you link some resource about why linear logic is a better algebra for beliefs than sigma algebra?
Would you be able to share Abram's answer in written form? I'd be keen to hear what he has to say.
More or less quoting from autogenerated subtitles:
So, this remains very speculative despite years of kind of thinking about this and I'm not saying something like "linear logic is just the right thing". I feel there is something deeply wrong about linear logic as well but I'll give my argument.
So my pitch is like this: we want to understand where does the sigma algebra come from or where does the algebra come from. And if it is a sigma algebra, could we justify that? And if it's not, what's the right appropriate thing that we get instead, that sort of naturally falls out? My argument that the thing that naturally falls out is probably more like linear logic than like a sigma algebra is like this.
As many of you may know I like logical induction a whole lot. I think that it's right to think of beliefs as not completely coherent and instead we want systems that have these approximately coherent beliefs. And how do you do that? Well a kind of generic way to do that is with a market because in a market any sort of easily computed non-coherence will be pumped out of the market by a trader who recognizes that incoherence and takes advantage of it for a money pump and thereby gains wealth and at some point has enough wealth that it's just enforcing that notion of coherence. I think that's a great picture but if we are imagining beliefs as having this kind of type signature of things on a market that can be traded then the natural algebra for beliefs is basically like an algebra of derivatives.
So we have a bunch of basic goods. Some of them represent probabilities because eventually, we anticipate that they take on the value zero or one. Some of them represent more general expectations as I've been arguing but we have these goods. The goods have values which are expectations and then we have ways of composing these goods together to make more goods. I don't have a completely satisfying picture here that says "Ah! It should be linear logic!" but it feels like if I imagine goods as these kinds of contracts then I naturally have something like a tensor. If I have good A and good B then I have a contract which is like "I owe you one A and one B and this is like a tensor. I naturally have the short of an object which is like the negation. So if I have good A and then somebody wants to short that good, then I can kind of make this argument for like all the other linear operators, like natural contract types.
If we put together a prediction market, we can force it to use classical logic if we want. That's what logical induction does. Logical induction gives us something that approximates classical probability distributions but only by virtue of forcing. The market maker is saying "I will allow any trades that enforce the coherence properties associated with classical logic". It's like: things are either true or false. Propositions are assumed to eventually converge to one or zero. We assume that there's not some unresolved proposition even though logical induction is manufactured to deal with logical uncertainty which means there are some undecidable propositions because we're dealing with general propositions in mathematics. So it's sort of enforcing this classicality with no justification. My hope there is like: Well, we should think about what falls out naturally from the idea of setting up a prediction market when the market maker isn't obsessed with classical logic. As I said it just seems like whatever it is it seems closer to the linear logic.
Abram also shared the paper: From Classical to Intuitionistic Probability.
Not sure this is exactly what you meant by the full preference ordering, but might be of interest: I give the preorder of universally-shared-preferences between "models" here (in section 4).
Basically, it is the Blackwell order, if you extend the Blackwell setting to include a system.
I was impressed by this post. I don't have the mathematical chops to evaluate it as math -- probably it's fairly trivial -- but I think it's rare for math to tell us something so interesting and important about the world, as this seems to do. See this comment where I summarize my takeaways; is it not quite amazing that these conclusions about artificial neural nets are provable (or provable-given-plausible-conditions) rather than just conjectures-which-seem-to-be-borne-out-by-ANN-behavior-so-far? (E.g. conclusions like "Neural nets trained on very complex open-ended real-world tasks/environments will build, remember, and use internal models of their environments... for something which resembles expected utility maximization!") Anyhow, I guess I shouldn't focus on the provability because even that's not super important. What matters is that this seems to be a fairly rigorous argument for a conclusion which many people doubt, that is pretty relevant to this whole AGI safety thing.
It's possible that I'm making mountains out of molehills here so I'd be interested to hear pushback. But as it stands I feel like the ideas in this post deserve to be turned into a paper and more widely publicized.
Appreciate this post! I had seen the good regulator theorem referenced every now and then, but wasn't sure what exactly the relevant claims were, and wouldn't have known how to go through the original proof myself. This is helpful.
(E.g. the result was cited by Frith & Metzinger as part of their argument that, as an agent seeks to avoid being punished by society, this constitutes an attempt to regulate society's behavior; and for the regulation be successful, the agent needs to internalize a model of the society's preferences, which once internalized becomes something like a subagent which then regulates the agent in turn and causes behaviors such as self-punishment. It sounds like the math of the theorem isn't very strongly relevant for that particular argument, though some form of the overall argument still sounds plausible to me regardless.)
Planned summary (edited in response to feedback):
Consider a setting in which we must extract information from some data X to produce M, so that it can later perform some task Z in a system S while only having access to M. We assume that the task depends only on S and not on X (except inasmuch as X affects S). As a concrete example, we might consider gradient descent extracting information from a training dataset (X) and encoding it in neural network weights (M), which can later be used to classify new test images (Z) taken in the world (S) without looking at the training dataset.
The key question: when is it reasonable to call M a model of S?
1. If we assume that this process is done optimally, then M must contain all information in X that is needed for optimal performance on Z.
2. If we assume that every aspect of S is important for optimal performance on Z, then M must contain all information about S that it is possible to get. Note that it is usually important that Z contains some new input (e.g. test images to be classified) to prevent M from hardcoding solutions to Z without needing to infer properties of S.
3. If we assume that M contains _no more_ information than it needs, then it must contain exactly the information about S that can be deduced from X.
It seems reasonable to say that in this case we constructed a model M of the system S from the source X "as well as possible". This post formalizes this conceptual argument and presents it as a refined version of the [Good Regulator Theorem](http://pespmc1.vub.ac.be/books/Conant_Ashby.pdf).
Returning to the neural net example, this argument suggests that since neural networks are trained on data from the world, their weights will encode information about the world and can be thought of as a model of the world.
Four things I'd change:
- In the case of a neural net, I would probably say that the training data is X, and S is the thing we want to predict. Z measures (expected) accuracy of prediction, so to make good predictions with minimal info kept around from the data, we need a model. (Other applications of the theorem could of course say other things, but this seems like the one we probably want most.)
- On point (3), M contains exactly the information from X relevant to S, not the information that S contains (since it doesn't have access to all the information S contains).
- On point (2), it's not that every aspect of S must be relevant to Z, but rather that every change in S must change our optimal strategy (when optimizing for Z). S could be relevant to Z in ways that don't change our optimal strategy, and then we wouldn't need to keep around all the info about S.
- The idea that information comes in two steps, with the second input "choosing which game we play", is important. Without that, it's much less plausible that every change in S changes the optimal strategy. With information coming in two steps, we have to keep around all the information from the first step which could be relevant to any of the possible games; our "strategy" includes strategies for the sub-games resulting from each possible value of the second input, and a change in any one of those is enough.
In the case of a neural net, I would probably say that the training data is X, and S is the thing we want to predict.
I was considering this, but the problem is that in your setup S is supposed to be derived from X (that is, S is a deterministic function of X), which is not true when X = training data and S = that which we want to predict.
On point (3), M contains exactly the information from X relevant to S, not the information that S contains (since it doesn't have access to all the information S contains).
If S is derived from X, then "information in S" = "information in X relevant to S"
On point (2), it's not that every aspect of S must be relevant to Z, but rather that every change in S must change our optimal strategy (when optimizing for Z). S could be relevant to Z in ways that don't change our optimal strategy, and then we wouldn't need to keep around all the info about S.
Fair point. I kind of wanted to abstract away this detail in the operationalization of "relevant", but it does seem misleading as stated. Changed to "important for optimal performance".
The idea that information comes in two steps, with the second input "choosing which game we play", is important.
I was hoping that this would come through via the neural net example, where Z obviously includes new information in the form of the new test inputs which have to be labeled. I've added the sentence "Note that it is usually important that Z contains some new input (e.g. test images to be classified) to prevent M from hardcoding solutions to Z without needing to look at S" to the second point to clarify.
(In general I struggled with keeping the summary short vs. staying true to the details of the causal model.)
I was considering this, but the problem is that in your setup S is supposed to be derived from X (that is, S is a deterministic function of X), which is not true when X = training data and S = that which we want to predict.
That's an (implicit) assumption in Conant & Ashby's setup, I explicitly remove that constraint in the "Minimum Entropy -> Maximum Expected Utility and Imperfect Knowledge" section. (That's the "imperfect knowledge" part.)
If S is derived from X, then "information in S" = "information in X relevant to S"
Same here. Once we relax the "S is a deterministic function of X" constraint, the "information in X relevant to S" is exactly the posterior distribution , which is why that distribution comes up so much in the later sections.
(In general I struggled with keeping the summary short vs. staying true to the details of the causal model.)
Yeah, the number of necessary nontrivial pieces is... just a little to high to not have to worry about inductive distance.
I explicitly remove that constraint in the "Minimum Entropy -> Maximum Expected Utility and Imperfect Knowledge" section.
... That'll teach me to skim through the math in posts I'm trying to summarize. I've edited the summary, lmk if it looks good now.
Good enough. I don't love it, but I also don't see easy ways to improve it without making it longer and more technical (which would mean it's not strictly an improvement). Maybe at some point I'll take the time to make a shorter and less math-dense writeup.
Thanks, this is really cool! I don't know much about this stuff so I may be getting over-hyped, but still.
I'd love to see a follow-up to this post that starts with the Takeaway and explains how this would work in practice for a big artificial neural net undergoing training. Something like this, I expect:
--There are lottery tickets that make pretty close to optimal decisions, and as training progresses they get increasingly more weight until eventually the network is dominated by one or more of the close-to-optimal lottery tickets.
--Because of key conditions 2 and 3, the optimal tickets will involve some sort of subcomponent that compresses information from X and stores it to later be combined with Y.
--Key condition 4 might not be strictly true in practice; it might not be that our dataset of training examples is so diverse that literally every way the distribution over S could vary corresponds to a different optimal behavior. And even if our dataset was that diverse, it might take a long time to learn our way through the entire dataset. However, what we CAN say is that the subcomponent that compresses information from X and stores it to later be combined with Y will increasingly (as training continues) store "all and only the relevant information," i.e. all and only the information that thus-far-in-training has mattered to performance. Moreover, intuitively there is an extent to which Y can "choose many different games," an extent to which the training data so far has "made relevant" information about various aspects of S. To the extent that Y can choose many different games -- that is, to the extent that the training data makes aspects of S relevant -- the network will store information about those aspects of S.
--Thus, for a neural network being trained on some very complex open-ended real-world task/environment, it's plausible that Y can "choose many different games" to a large extent, such that the close-to-optimal lottery tickets will have an information-compressing-and-retaining subcomponent that contains lots of information about S but not much information about X. In particular it in some sense "represents all the aspects of S that are likely to be relevant to decision-making."
--Intuitively, this is sufficient for us to be confident in saying: Neural nets trained on very complex open-ended real-world tasks/environments will build, remember, and use internal models of their environments. (Maybe we even add something like ...for something which resembles expected utility maximization!)
Anyhow. I think this is important enough that there should be a published paper laying all this out. It should start with the theorem you just proved/fixed, and then move on to the neural net context like I just sketched. This is important because it's something a bunch of people would want to cite as a building block for arguments about agency, mesa-optimizers, human modelling, etc. etc.
Your bullet points are basically correct. In practice, applying the theorem to any particular NN would require some careful setup to make the causal structure match - i.e. we have to designate the right things as "system", "regulator", "map", "inputs X & Y", and "outcome", and that will vary from architecture to architecture. But I expect it can be applied to most architectures used in practice.
I'm probably not going to turn this into a paper myself soon. At the moment, I'm pursuing threads which I think are much more promising - in particular, thinking about when a "regulator's model" mirrors the structure of the system/environment, not just its black-box functionality. This was just a side-project within that pursuit. If someone else wants to turn this into a paper, I'd be happy to help, and there's enough technical work to be done in applying it to NNs that you wouldn't just be writing up this post.
Doesn't sound like a job for me, but would you consider e.g. getting a grant to hire someone to coauthor this with you? I think the "getting a grant" part would not be the hard part.
Yeah, "get a grant" is definitely not the part of that plan which is a hard sell. Hiring people is a PITA. If I ever get to a point where I have enough things like this, which could relatively-easily be offloaded to another person, I'll probably do it. But at this point, no.
Maybe related: A paper likely to get an oral at ICLR 2024. I haven't read it, but I think it substantially improves on the Good Regulator Theorem. I think their Theorem 1 shows that from an optimal policy, you can identify (deduce) the exact causal model of the data generating process, and Theorem 2 shows that from a policy satisfying regret bounds, you can identify an approximate causal model. The assumptions are far weaker and more realistic than being the simplest policy that can perfectly regulate some variable.
Robust agents learn causal world models
[...]
We prove that agents that are capable of adapting to distributional shifts must have learned a causal model of their environment, establishing a formal equivalence between causality and transfer learning.

Later information can “choose many different games” - specifically, whenever the posterior distribution of system-state given two possible values is different, there must be at least one value under which optimal play differs for the two values.
Given your four conditions, I wonder if there's a result like "optimally power-seeking agents (minimizing information costs) must model the world." That is, I think power is about being able to achieve a wide range of different goals (to win at 'many different games' the environment could ask of you), and so if you want to be able to sufficiently accurately estimate the expected power provided by a course of action, you have to know how well you can win at all these different games.
Yes! That is exactly the sort of theorem I'd expect to hold. (Though you might need to be in POMDP-land, not just MDP-land, for it to be interesting.)
Note on notation...
You can think of something like as a python dictionary mapping x-values to the corresponding values. That whole dictionary would be a function of Y. In the case of something like , it's a partial policy mapping each second-input-value y and regulator output value r to the probability that the regulator chooses that output value on that input value, and we're thinking of that whole partial policy as a function of the first input value X. So, it's a function which is itself a random variable constructed from X.
The reason I need something like this is because sometimes I want to say e.g. "two policies are identical" (i.e. P[R=r|X=x] is the the same for all r, x), sometimes I want to say "two distributions are identical" (i.e. two X-values yield the same output distribution), etc, and writing it all out in terms of quantifiers makes it hard to see what's going on conceptually.
I've been trying to figure out a good notation for this, and I haven't settled on one, so I'd be interested in peoples' thoughts on it. Thankyou to TurnTrout for some good advice already; I've updated the post based on that. The notation remains somewhat cumbersome and likely confusing for people not accustomed to dense math notation; I'm interested in suggestions to improve both of those problems.
the regulator could just be the identity function: it takes in and returns . This does not sound like a “model”.
What is the type signature of the regulator? It's a policy on state space , and it returns states as well? Are those its "actions"? (From the point of view of the causal graph, I suppose just depends on whatever the regulator outputs, and the true state , so maybe it's not important what the regulator outputs. Just that by the original account, any deterministic regulator could be "optimal", even if it doesn't do meaningful computation.)
That's the right question to ask. Conant & Ashby intentionally leave both the type signature and the causal structure of the regulator undefined - they have a whole spiel about how it can apply to multiple different setups (though they fail to mention that in some of those setups - e.g. feedback control - the content of the theorem is trivial).
For purposes of my version of the theorem, the types of the variables themselves don't particularly matter, as long as the causal structure applies. The proofs implicitly assumed that the variables have finitely many values, but of course we can get around that by taking limits, as long as we're consistent about our notion of "minimal information".
Vivek points out the following variant. If the effects of the regulator and system are both modulated by some intermediate functions which are deterministic.
Then the "consequential parts" of every good regulator R (defined as the parts of R's state whose information is preserved by the intermediate function) are a deterministic function of the consequential parts of every system S. This is also technically implied by the lemma, but framing it this way makes it more clear.
Intuitive argument: The lemma implies that is a deterministic function of . The "simplest regulator" assumption on says that is a deterministic function of . We can propagate this back to the "consequential parts" of R and S.
This is meaningful because the real world often throws away information from the perspective of agents. It might be useful in a selection theorem that starts with optimization as a premise.
Note for others: this is a variant of the original Good Regulator theorem. In particular, it assumes that the regulator R has perfect information about system state S, which is why is able to be a deterministic function of .
A while back I was looking for toy examples of environments with different amounts of 'naturalness' to their abstractions, and along the way noticed a connection between this version of Gooder Regulator and the Blackwell order.
Inspired by this, I expanded on this perspective of preferences-over-models / abstraction a fair bit here.
It includes among other things:
- the full preorder of preferences-shared-by-all-agents over maps (vs. just the maximum)
- an argument that actually we want to generalize to this diagram instead[1] :
- an extension to preferences shared by 'most' agents based on Turner's power-seeking theorems (and a formal connection to power-seeking)
Personally I think these results are pretty neat; I hope they might be of interest.
I also make one other argument there that directly responds to this post, re: the claim:
[The] “model” M definitely has to store exactly the posterior.
I think this sort of true, depending how you interpret it, but really it's more accurate to say the whole regulator has to encode the posterior, not just .
Specifically, as you show, and must induce the same equivalence classes of . This means that they are isomorphic as functions in a particular sense.
But it turns out: lots of (meaningfully) different systems can lead to the same optimal model . This means you can't recover the full system transition function just by looking at ; so it doesn't really store the whole posterior.
On the other hand, you can uniquely recover the whole posterior (up to technicalities) from plus the agent's optimal strategies . So it is still fair to say the agent as a whole most model the Bayesian posterior; but I'd say it's not just the model which does it.
- ^
Which in this perspective basically means allowing the 'system' or 'world' we study to include restrictions on the outcome mapping, e.g. that , and lead to the same outcome, which must be given a common utility by any given game. Looking back at this again, I'm not sure I described the distinction quite right in my post (since this setting as you gave it already has a distinct from ), but there is still a distinction.
Trying to think about this from more of a practical machine learning standpoint, but without full understanding of all the points you made...
I think in the case where X, Y, and S are all partially but not fully known, and you have to choose model M so as to minimize regret over time. Two things occur to me as possibly useful strategies for choosing M. You might find the opportunity to run 'experiments', to choose suboptimal output R at an early timestep such that from then on you'd have a better understanding of S, and be able to better refine M for future timesteps.
The other thing that occurs to me is that if the distributions of X and Y are unknown and you have some approximation of them, then perfectly fitting M to those approximations would potentially be overfitting. If you know you have only approximations, then you'd want to not fully minimize M but instead leave some 'wiggle room' for probable future cases of X and Y. You could even tailor this based on patterns you've seen in X and Y. Like, if X was gaussian noise, but the mean seemed to be roughly following a sine wave for n cycles, then a square wave for n cycles, then a triangular wave for n cycles, you'd be reasonably justified in guessing that there would be a new repeating wave shape coming up which would repeat for n cycles. You'd want to leave room in the model to account for this.
Perhaps someone who understands the post more completely can let me know if I seem to be on the right track for understanding and extrapolating from this.
Conant & Ashby’s “Every Good Regulator Of A System Must Be A Model Of That System” opens with:
This may be the most misleading title and summary I have ever seen on a math paper. If by “making a model” one means the sort of thing people usually do when model-making - i.e. reconstruct a system’s variables/parameters/structure from some information about them - then Conant & Ashby’s claim is simply false.
What they actually prove is that every regulator which is optimal and contains no unnecessary noise is equivalent to a regulator which first reconstructs the variable-values of the system it’s controlling, then chooses its output as a function of those values (ignoring the original inputs). This does not mean that every such regulator actually reconstructs the variable-values internally. And Ashby & Conant’s proof has several shortcomings even for this more modest claim.
This post presents a modification of the Good Regulator Theorem, and provides a reasonably-general condition under which any optimal minimal regulator must actually construct a model of the controlled system internally. The key idea is conceptually similar to some of the pieces from Risks From Learned Optimization. Basically: an information bottleneck can force the use of a model, in much the same way that an information bottleneck can force the use of a mesa-optimizer. Along the way, we’ll also review the original Good Regulator Theorem and a few minor variants which fix some other problems with the original theorem.
The Original Good Regulator Theorem
We’re interested mainly in this causal diagram:
The main goal is to choose the regulator policy P[R|X] to minimize the entropy of outcome Z. Later sections will show that this is (roughly) equivalent to expected utility maximization.
After explaining this problem, Conant & Ashby replace it with a different problem, which is not equivalent, and they do not bother to point out that it is not equivalent. They just present roughly the diagram above, and then their actual math implicitly uses this diagram instead:
Rather than choosing a regulator policy P[R|X], they instead choose a policy P[R|S]. In other words: they implicitly assume that the regulator has perfect information about the system state (and their proof does require this). Later, we’ll talk about how the original theorem generalizes to situations where the regulator does not have perfect information. But for now, I’ll just outline the argument from the paper.
We’ll use two assumptions:
The main lemma then says: for any optimal regulator P[R|S], Z is a deterministic function of S. Equivalently: all R-values r with nonzero probability (for a given S-value s) must give the same Z(r,s).
Intuitive argument: if the regulator could pick two different Z-values (given S), then it can achieve strictly lower entropy by always picking whichever one has higher probability P[Z] (unconditional on S). Even if the two have the same P[Z], always picking one or the other gives strictly lower entropy (since the one we pick will end up with higher P[Z] once we pick it more often). If the regulator is optimal, then achieving strictly lower entropy is impossible, hence it must always pick the same Z-value given the same S-value. For that argument unpacked into a formal proof, see the paper.
With the lemma nailed down, the last step in Conant & Ashby’s argument is that any remaining nondeterminism in P[R|S] is “unnecessary complexity”. All R-values chosen with nonzero probability for a given S-value must yield the same Z anyway, so there’s no reason to have more than one of them. We might as well make R a deterministic function of S.
Thus: every “simplest” optimal regulator (in the sense that it contains no unnecessary noise) is a “model” of the system (in the sense that the regulator output R is a deterministic function of the system state S).
The Problems
There are two immediate problems with this theorem:
Also, though I don’t consider it a “problem” so much as a choice which I think most people here will find more familiar:
We’ll address all of these in the next few sections. Making the notion of “model” less silly will take place in two steps - the first step to make it a little less silly while keeping around most of the original’s meaning, the second step to make it a lot less silly while changing the meaning significantly.
Making The Notion Of “Model” A Little Less Silly
The notion of “model” basically says “R is a model of S iff R is a deterministic function of S” - the idea being that the regulator needs to reconstruct the value of S from its inputs in order to choose its outputs. But the proof-as-written-in-the-paper assumes that R takes S as an input directly (i.e. the regulator chooses P[R|S]), so really the regulator doesn’t need to “model” S in any nontrivial sense in order for R to be a deterministic function of S. For instance, the regulator could just be the identity function: it takes in S and returns S. This does not sound like a “model”.
Fortunately, we can make the notion of “model” nontrivial quite easily:
The whole proof actually works just fine with these two assumptions, and I think this is what Conant & Ashby originally intended. The end result is that the regulator output R must be a deterministic function of S, even if the regulator only takes X as input, not S itself (assuming S is a deterministic function of X, i.e. the regulator has enough information to perfectly reconstruct S).
Note that this still does not mean that every optimal, not-unnecessarily-nondeterministic regulator actually reconstructs S internally. It only shows that any optimal, not-unnecessarily-nondeterministic regulator is equivalent to one which reconstructs S and then chooses its output as a deterministic function of S (ignoring X).
Minimum Entropy -> Maximum Expected Utility And Imperfect Knowledge
I think the theorem is simpler and more intuitive in a maximum expected utility framework, besides being more familiar.
We choose a policy function (x,r↦P[R=r|X=x]) to maximize expected utility. Since there’s no decision-theoretic funny business in this particular setup, we can maximize for each X-value independently:
max(x,r↦P[R=r|X=x])∑X,R,S,Zu(Z)P[Z|R,S]P[R|X]P[S|X]P[X]
=∑XP[X](max(r↦P[R=r|X])∑R,S,Zu(Z)P[Z|R,S]P[R|X]P[S|X])
Key thing to note: when two X-values yield the same distribution function (s↦P[S=s|X]), the maximization problem
max(r↦P[R=r|X])∑R,S,Zu(Z)P[Z|R,S]P[R|X]P[S|X]
… is exactly the same for those two X-values. So, we might as well choose the same optimal distribution (r↦P[R=r|X]), even if there are multiple optimal options. Using different optima for different X, even when the maximization problems are the same, would be “unnecessary complexity” in exactly the same sense as Conant & Ashby’s theorem.
So: every “simplest” (in the sense that it does not have any unnecessary variation in decision distribution) optimal (in the sense that it maximizes expected utility) regulator is a deterministic function of the posterior distribution of the system state (s↦P[S=s|X]). In other words, there is some equivalent regulator which first calculates the Bayesian posterior of S given X, then throws away X and computes its output just from that distribution.
This solves the “imperfect knowledge” issue for free. When input data X is not sufficient to perfectly estimate the system state S, our regulator output is a function of the posterior distribution of S, rather than S itself.
When system state can be perfectly estimated from inputs, the distribution (s↦P[S=s|X]) is itself a deterministic function of S, therefore the regulator output will also be a deterministic function of S.
Important note: I am not sure whether this result holds for minimum entropy. It is a qualitatively different problem, and in some ways more interesting - it’s more like an embedded agency problem, since decisions for one input-value can influence the optimal choice given other X-values.
Making The Notion Of “Model” A Lot Less Silly
Finally, the main event. So far, we’ve said that regulators which are “optimal” and “simple” in various senses are equivalent to regulators which “use a model” - i.e. they first estimate the system state, then make a decision based on that estimate, ignoring the original input. Now we’ll see a condition under which “optimal” and “simple” regulators are not just equivalent to regulators which use a model, but in fact must use a model themselves.
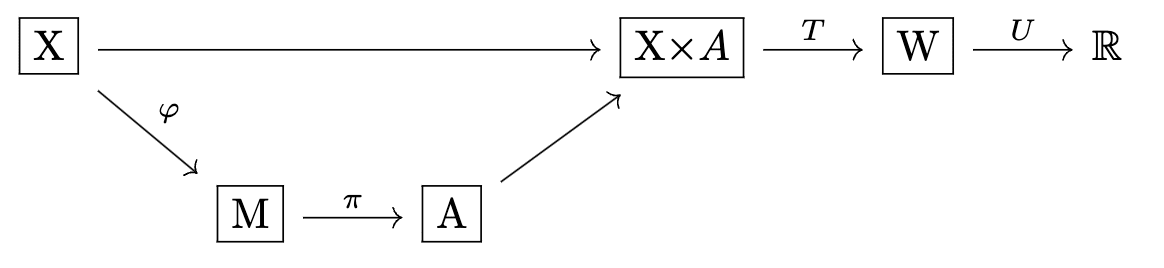
Here’s the new picture:
Our regulator now receives two “rounds” of data (X, then Y) before choosing the output R. In between, it chooses what information from X to keep around - the retained information is the “model” M. The interesting problem is to prove that, under certain conditions, M will have properties which make the name “model” actually make sense.
Conceptually, Y “chooses which game” the regulator will play. In order to achieve optimal play across all “possible games” Y might choose, M has to keep around any information relevant to any possible game. However, each game just takes S as input (not X directly), so at most M has to keep around all the information relevant to S. So: with a sufficiently rich “set of games” (r,z↦P[Z=z|R=r,S,Y]), we expect that M will have to contain all information from X relevant to S.
On the flip side, we want this to be an information bottleneck: we want M to contain as little information as possible (in an information-theoretic sense), while still achieving optimality. Combining this with the previous paragraph: we want M to contain as little information as possible, while still containing all information from X relevant to S. That’s exactly the condition for the Minimal Map Theorem: M must be (isomorphic to) the Bayesian distribution (s↦P[S=s|X]).
That’s what we’re going to prove: if M is a minimum-information optimal summary of X, for a sufficiently rich “set of games”, then M is isomorphic to the Bayesian posterior distribution on S given X, i.e. (s↦P[S=s|X]). That’s the sense in which M is a “model”.
As in the previous section, we can independently optimize for each X-value:
max(x,y,r↦P[R=r|X=x,Y=y])∑X,Y,R,S,Zu(Z)P[Z|R,S,Y]P[R|X,Y]P[S|X]P[X]P[Y]
=∑XP[X](max(y,r↦P[R=r|X,Y=y])∑Y,R,S,Zu(Z)P[Z|R,S,Y]P[R|X,Y]P[S|X]P[Y])
Conceptually, our regulator sees the X-value, then chooses a strategy (y,r↦P[R=r|X,Y=y]), i.e. it chooses the distribution from which R will be drawn for each Y value.
We’ll start with a simplifying assumption: there is a unique optimal regulator P∗[R|X,Y]. (Note that we’re assuming the full black-box optimal function of the regulator is unique; there can still be internally-different optimal regulators with the same optimal black-box function, e.g. using different maps M.) This assumption is mainly to simplify the proof; the conclusion survives without it, but we would need to track sets of optimal strategies everywhere rather than just “the optimal strategy”, and the minimal-information assumption would ultimately substitute for uniqueness of the optimal regulator.
If two X-values yield the same Bayesian posterior (s↦P[S=s|X]), then they must yield the same optimal strategy (y,r↦P∗[R=r|X,Y=y]). Proof: the optimization problems are the same, and the optimum is unique, so the strategy is the same. (In the non-unique case, picking different strategies would force M to contain strictly more information - i.e. M(X)≠M(X′) - so the minimal-information optimal regulator will pick identical strategies whenever it can do so. Making this reasoning fully work with many optimal X-values takes a bit of effort and doesn’t produce much useful insight, but it works.)
The next step is more interesting: given a sufficiently rich set of games, not only is the strategy a function of the posterior, the posterior is a function of the strategy. If two X-values yield the same strategy (y,r↦P∗[R=r|X,Y=y]), then they must yield the same Bayesian posterior (s↦P[S=s|X]). What do we mean by “sufficiently rich set of games”? Well, given two different distributions (s↦P[S=s|X]) and (s↦P[S=s|X′]), there must be some particular Y-value yp for which the optimal strategy (r↦P∗[R=r|X,Y=yp]) is different from (r↦P∗[R=r|X′,Y=yp]). The key is that we only need one Y-value for which the optimal strategies differ between X and X′.
So: by “sufficiently rich set of games”, we mean that for every pair of X-values with different Bayesian posteriors (s↦P[S=s|X]), there exists some Y-value for which the optimal strategy (r↦P∗[R=r|X,Y]) differs. Conceptually: “sufficiently rich set of games” means that for each pair of two different possible posteriors (s↦P[S=s|X]), Y can pick at least one “game” (i.e. optimization problem) for which the optimal policy is different under the two posteriors.
From there, the proof is easy. The posterior is a function of the strategy, the strategy is a function of M, therefore the posterior is a function of M: two different posteriors (s↦P[S=s|X]) and (s↦P[S=s|X′]) must have two different “models” M(X) and M(X′). On the other hand, we already know that the optimal strategy is a function of (s↦P[S=s|X]), so in in order for M to be information-minimal it must not distinguish between X-values with the same posterior (s↦P[S=s|X]). Thus: M(X)=M(X′) if-and-only-if (s↦P[S=s|X])=(s↦P[S=s|X′]). The “model” M(X) is isomorphic to the Bayesian posterior (s↦P[S=s|X]).
Takeaway
When should a regulator use a model internally? We have four key conditions:
Conceptually, because we don’t know what game we’re going to play, we need to keep around all the information potentially relevant to any possible game. The minimum information which can be kept, while still keeping all the information potentially relevant to any possible game, is the Bayesian posterior on system state S. There’s still a degree of freedom in how we encode the posterior on S (that’s the “isomorphism” part), but the “model” M definitely has to store exactly the posterior.