Abstract: Values alignment, in AI safety, is typically construed as the imbuing into artificial intelligence of human values, so as to have the artificial intelligence act in ways that encourage what humans value to persist, and equally to preclude what humans do not value. “Anthropocentric” alignment emphasises that the values aligned-to are human, and what humans want. For, practically, were values alignment achieved, this means the AI is to act as humans want, and not as they do not want (for if humans wanted what they did not value, or vice versa, they would not seek, so would not act, to possess the want and value; as the AI is to act for them, for their wants and values: “Want implies act”. If not acted upon, what is valued may be lost, then by assumption is no longer present to be valued; consistency demands action, preservation). We shall show that the sets, as it were, of human wants and of possible actions, are incommensurable, and that therefore anthropocentric-alignment is impossible, and some other “values” will be required to have AI “align” with them, can this be done at all.

Epistemic status: This is likely the most mathematically ambitious production by one so ill-educated they had to teach themselves long division aged twenty-five, in human history (Since there may not be much more human history, it may retain this distinction). Minor errors and logical redundancies are likely; serious mistakes cannot be discounted, and the author has nothing with which to identify them. Hence, the reader is invited to comment, as necessary, to highlight and correct such errors – not even for this author’s benefit as much as for similarly non-technical readers, who, were it only thoroughly downvoted, might receive no “updating” of their knowledge were they not given to know why it is abominated; they may even promulgate it in a spirit of iconoclasm – contrary to downvote’s intention; hence “voting” is generally counterproductive. Every effort has been made to have it be accessible to the non-technical reader, to the point of pedantry (“Spare the parentheses” – spoil the proof).

(Too, voting is actively cruel, since it gives karma, and karma is what makes you go to hell: to vote is to wish someone to hell, or worse, to heaven, no reason given; presumably “karma” was a witticism, in LessWrong’s materialist founding. It is not funny. It is cruel and counterproductive. Strange too, no-one seems to have noted the cruelty previously.)

1.1 Introduction

In artificial intelligence safety research, the final goal and hope, is alignment – values alignment; the values are of humanity. We refer to this goal, then, as “anthropocentric-alignment” – AI is safe, and for humanity, that AI enacts human goals, preserves human values – and in short, in anthropocentric alignment, what humans want, including their survival, they get. For were there no interchangeability with what humans value, and want, the latter implying some action to procure or protect what is valued, the latter is apt to be lost, on any long-enough timeline, and then, no longer existing, so no longer possible, it is no longer available to be valued. Thus, we take human values and wants as interchangeable.

In AGI Ruin, Yudkowsky maintains that there are two methods to attain anthropocentric alignment: Coherent Extrapolated Volition, in which an artificial superintelligence determines what humanity wants, and enacts the want – and corrigibility, in which the AI enacts human’s instruction, so long as whatever its actions and circumstances are or may come to be, it still can have its actions terminated by humans at any time, without restriction of this possibility of termination.

We might refer to these respectively as indirectly normative anthropocentric-alignment, versus directly normative anthropocentric-alignment. For, as noted in “Worldwork for Ethics”, both of these are subsets of anthropocentric-alignment, inasmuch as they enact human wants, either continuously and totally, in CEV, or piecemeal, in corrigibility (in the latter case, with a continuous want that human control is to remain enacted, or possible). In succeeding sections we will demonstrate how each can be represented as sets of vectors in suitably defined vector spaces. Separately, the actions actually undertaken in certain physical situations we will also have represented in a vector space (or rather, as shall be detailed, as a vector “pseudo-space”; though for simplicity we shall tend to refer to it as a “space”).

With vector spaces representing the spaces of human wants and possible actions, then, anthropocentric-alignment in general must be construed as a bijection between the elements of these spaces, that is, that for every human want that a given situation should obtain, there be some action to make that situation obtain. For if there should be some want for which no action can fulfill it, first, total alignment of AI with wants is impossible, in which case alignment per se, is impossible; and moreover, if pursuing an impossible want, the AI may, if it is not able or not programmed to ascertain the impossibility, tend to deploy the maximum possible resources to obtain it, in an attempt to instantiate the want, though it’s impossibility yields obstacles which the AI erroneously reasons might be overcome with yet more resources; this may occur if AI is “duty-bound” in full anthropocentric-alignment to fulfill every human want, however impractical, and without regard to possibility – such a process would yield infrastructure profusion. And finally, if some want should be physically obtainable but contradictory inasmuch as it precludes humans wanting anything else, even in the case in which actions can indeed be bijected onto wants, the result in this future-excluding case, must be human destruction and an end to all that is known to be valued and valuable, hence too, a breaking of alignment.

(Remark: curiously, as alignment is construed as a bijection between sets of wants and of actions, then AI in general, and ASI particularly, must be regarded as a bijective function, rather than a more or less autonomous entity. As ASI contrarily is an entity, or agent, the establishment of a bijection is all the more difficult).

It must be emphasised that the aforementioned spaces are not analogies – as we shall utilize the axioms of vector spaces or of linear algebra, our use of concrete, albeit undefined terms, as of “want”, “plan”, or “action”, we are establishing a model of the vector space axioms, so our work will establish a branch of applied mathematics (Eves 1990). And it is somewhat natural we should use vectors in this way, since in deep neural nets, concepts are represented by embeddings of vectors connecting parameters.

By our work we will establish the incommensurability between the “want space” and the “action space”, that no bijection between them obtains. Accordingly, we will show that “anthropocentric-alignment”, “values-alignment”, as it has hitherto been known, is impossible, and so is the present paradigm of alignment impossible, itself. We will explore some alternatives in the conclusion.

1.2 Definitions

From the Oxford Concise Dictionary of Mathematics (5^th edition), a vector space is defined as the mathematical structure defined by two sets, and their associated operations, and possessing the following properties:

1. The set A of vectors, must form an Abelian group, i.e. it requires an operation of addition to be defined on the set; to be closed under addition; to be commutative, and to have an identity and inverse elements
2. The set B of scalars must form a field, i.e. be an Abelian group with respect to addition, an Abelian group with respect to multiplication when the zero element is removed, and for multiplication to be distributed over addition
3. A multiplication operation defined on the two sets with the properties, for scalars p, q, in set B, and x, y, vectors in set A, that 

p(x+ y) = p(x) + p(y)

(p + q)x = (p)x + (q)x

p(qx) = (pq)x

iv) If 1 is the multiplicative identity in set B, then 1(x) = x.

1.2.1 Initial Qualities of Want, Action Spaces

First, we introduce our concepts, via undefined terms “want”, “plan”, “action”, “situation”, “state of affairs”. We intend to represent states of affairs in the world, actual, or idealized and in mind, to be represented as points in our vector space. From an initial position of wanting or doing nothing, our vectors represent our want to have another state of affairs to exist, and in the case of our actions, our efforts to make this state of affairs subsist. These we refer to respectively as the “want space” and “action space”. The scalar part of each vector represents respectively the “degree of desire”, or else the amount of energy or resources devoted to achieving the state of affairs that would result from an action. 

All vectors can be decomposed into a sum of basis vectors, each oriented along only one dimension of the vector space, multiplied by a scalar component determining the magnitude of the basis vector in that direction. The basis vectors are mutually orthogonal, and the sum of all basis vectors, is the given vector. In this interpretation, the basis vectors represent all the elements of a given state of affairs, and the extent to which they form a given situation. In general, the sums of vectors represent successive wants or actions in movements from situation to “further” situation. We assume no uncertainty either about what the situation is, to who wants it or acts to achieve it, as the situation is representable as data relating each situational element to every other. The want space consists of the certain situation, and the “will” or “desire” to have this situation obtain, or of actions, the resources expended for the same.

Let it be noted now, we must specially define which vector sums are elements of the action space, and for it, not all the features of a vector space are included; accordingly we will come to call the action space a representative of a vector “pseudo-space”, following our demonstration that as presented, wants and actions will indeed otherwise fulfill the definition of vector spaces. 

First we emphasise a crucial component of this applied branch of mathematics: all vectors and all sums of vectors in the analysis must exhibit the property of “possibility” or “achievability”, whereby all such vectors, except the vector-sum “v + (-v)” and its converse, must have a finite, non-zero norm (the norm being the operation of taking the numerical value of the vector’s basis vectors, squaring each, and all such squares summed together, with the square root of the sum of squares taken). We require these definitions to be in place as a guard against contradiction: states of affairs that can be described but not achieved, e.g., a mountain made of gold – whose mass might collapse its non-gold bases, thence to fall and no longer be a mountain, or, in an all-gold environment, perhaps so much mass that it is impossible for any part of it to extent beyond the others, whereupon a mountain is impossible, so a contradiction. The case “(-v) + v” and (in the want space) its commutative formula are only permitted to have a zero vector, as being the impulse or action, and an equal, opposite impulse not to act, are not contradictory, for they require no subsidiary action that would contradict the stasis.

A curious second form of contradiction is one in which there is no finite norm, though it is greater than zero. Such an instance is Cantor’s paradox, which is contradictory by dint of its definitions, less its operations. Since our criteria for vectors is “achievability”, an infinite norm, referent to a vector that is to obtain in actual world or mind, is contradictory in this way. Here the contradiction of a mountain of gold lies in a total alteration of physics to have it – which alteration alters the want of a mountain of gold, as well as its possibility of being had.

(Remark: “Plans”, we take in the sense of algorithms describing actions undertaken to establish a state of affairs. Despite the discrete-step nature of such algorithmic plans, the end state of affairs of such a plan is identical to that of a want. Plans then we take as isomorphic to want vectors, composed of some set of vector-sums; the norms of each, given the same end-point as a state of affairs, will be equal, so for simplicity we regard wants and plans as interchangeable, and refer exclusively to the set of possible wants, as vectors).

1.2.2 Applicability of Vector Space Axioms to Want, Actions Spaces

• Wants and actions can be compounded additively, as a sequence, so that addition is an operation defined for each.
• Since wants and actions profuse the space, be they so often added, they still will be wants and actions, so each is closed under addition.
• Desire or resources applied to want or action leave them as a want or action, so each is closed under multiplication.
• Wants can be compounded in any order, so are associative (Abelian) under addition in the spaces, as wants and actions are cumulative to a given end-situation.
• Wants are commutative, being unrestricted in imagination; commutation is restricted on the action space, whence it is a “pseudo-space”, as will be detailed in section two.
• There exists a zero vector of no motion in volition or action, for wants and actions.
• There exists an additive inverse want of a situation being returned to its unchanged state. Because we must well-order the action space, as will be detailed in section two, we must have (-v) + v = 0 for the action space, as a fictitious negative action forestalling in advance an action that then never is performed.
• Multiplication is distributive as desire or resources to compounded states of affairs as is representative of an impulse to have each, together; it is distributive, e.g., α(x + y) = α(x) + α(y).
• Scalar multiplication is distributive, {α(β)x = [α(β)]x}, as desire and resources redoubled, are redoubled.
• Identity element of want is contentment; (I + x) = (x + I) = x. For action, it is that x’s situation is the sum of fictional countervailing action and that same action: x + [(-x) + x] = x; so that the formula ((-x) + x) is the identity element of the action space.
• The zero vector of a desire for no change, or the result of no change in state of affairs to the present state of affairs, holds, that x + 0 = 0 + x = x, or: x + ((-x) + x) = ((-x) + x) + x = 0. It alone has a norm equal to zero. A want to retain a situation, or a fictional action versus an action to change a situation.
• The multiplicative identity element is a scalar such that I(x) = (x)I = x. This is respectively the desire specifically to retain a state of affairs, or the action of such maintenance as is required to retain it. 

(Remark: CEV and corrigibility in these representations are respectively all the vectors representing human wants bijected onto action vectors to fulfill them, simultaneously; and those wants corresponding to an action piecemeal, until a bijection is achieved – all while a prevailing want for human control is continuously enacted, and no action is an inverse vector to this want and action. Mutually bijective so, we regard CEV and corrigibility as isomorphic and interchangeable, hence both are “anthropocentric-alignment”, as noted in previous essays. N.B. also: curiously for both posited vector spaces, world-states would intrinsically, by the quantity of their basis vectors, hence the magnitude of their norms, represent the “complexity” of the situation described by the vector. Hence the world-states as represented by vectors, would have an intrinsic “utility” if greater complexity of the situation is considered as more desirable, since there would be more in the situation to desire, hence, greater utility in general.)

Whence, from all of these, and their bulleted applicability to our want space and action space, we find ourselves justified in regarding these as vector spaces, or, in the case of the action space, a “pseudo-space”, as is now to be shown.

2.1 Refining the Action Space 

We noted in section 1.2, that to justify the description of an action “pseudo-space” – whereas we exclude no axioms of vector spaces, yet we do exclude as undefined, certain elements of the want space vis-à-vis the action space.

A hackneyed example: we stand at the edge of a field, and throw a handball into its center: a state of affairs we call collectively the vector “u”, from a nullity of standing without change, to changing by our throw. We walk to the center of the field and pick up our thrown ball; this situational alteration we denote “v”.

Now, we can want to first walk to the center, then at once, in a time discontinuity, be at the edge throwing into the center, without intermediary motion to the edge. A norm-defying – so possibility-defying –contradiction would come in the form of “throw and not throw”. Whereas, such a discontinuity as this, whereas it may be physically impossible, is not per se contradictory and so, for the purpose of wanting, all vector sums of the want space commute, as required. 

Likewise an instance of (u + (-u)) would be to want to throw the handball back and forth again, in any order.

As justification that even unachievable wants still can be wanted, we appeal to Hume: “[A] passion can never, in any sense, be called unreasonable, but when founded on a false supposition, or when it chooses means insufficient for the designed end, ‘tis impossible, that reason and passion can ever oppose each other, or dispute for the government of the will and actions. The moment we perceive the falshood [sic] of any supposition, or the insufficiency of any means[,] our passions yields to our reason without any opposition. I may desire any fruit as of an excellent relish; but whenever you convince me of my mistake, my longing ceases. I may will the performance of certain actions as means of obtaining any desired good; but as my willing of these actions is only secondary, and founded on the supposition, that they are causes of the proposed effect; as soon as I discover the falshood [sic] of that supposition, they must become indifferent to me.” Emphasis added; (Hume, David. “A Treatise of Human Nature”, [hereafter: “Treatise”] Book II, Part III, Section III).

Now, we can imagine many situations in which first a handball finds its way into a field, and afterward we find ourselves with it in hand at the periphery. In short: if the means to attain our want are indifferent to us, and we do not think of them, we are assured (and Hume agrees), that we are not convinced of our want’s impossibility. Hence, we can want them, and they must be present in our want space. Non-contradictory wants, however impracticable, have a valid home in our minds, so in our wanting there.

Our action space, by contrast, must be not only non-contradictory, but also fully realizable, according to the known, as well as actual, laws of physics, as it is to denote actual actions, in the actual world; in the action space, causality must hold. 

We represent this, and the progression of time co-incidental with it, in the consideration that entropy of states of affairs must increase over time; a situation with lesser entropy must ever precede one of greater entropy. Hence a situation of a ball having been thrown by us, must be proceeded by the situation of our throwing, making it be thrown: from the hackneyed example, we must have (u + v), as a member of our action space, and exclude the possibility of (v + u).

We consider a set of all possible vectors of situations, and sums of such vectors, consistent with their being possible, as having a norm; this set, e.g., (u + v) and (v + u), which we will refer to respectively as a “commute” and an “anti-commute”, constitutes the want space.

To form the action space, we must appeal to Zermelo’s Well-ordering Theorem, to establish a dyadic relation “<”, for the action space, to render all elements well-ordered with respect to the value of the vector norms, least to greatest.

Next, consider the set of all disjoint subsets of vector sums, all commute and anti-commute pairs. From these disjoint subsets, we use the axiom of choice to select all the commutes (so the first vector in any vector sum vide actions, is less than the second, with respect to their number of basis vectors, hence norms, representing increasing entropic complexity with time; simpler preceding more entropically complex, e.g., for |u| < |v|, with respect to norms (u + v); never (v + u), in the action space). The set of all these commutes, and all vectors as singletons, well ordered least to greatest, represents the action space. We require also that sums of the form ((-v) + v), must be selected by the axiom of choice so that the negatively valued vector appears first, for by assumption we cannot reverse entropy’s progression.

We must appeal to these two uses of the axiom of choice, to ensure a well-ordering even in cases of unexaminably increasing values of vector norms – and the axiom of choice upon these norms, to establish as it were mere “entropic well-ordering”. Only with the axiom of choice can we choose only commutes or anti-commutes to form the action space, with norm sums becoming unexaminably large.

2.2 Conjecture: Entropic Invariants

(Remark: Hume notes (“Treatise”, Book I, Part III, Section III), we cannot perceive causality, in the form of cause and effect. Mathematical physics, describes relations of phenomena, but not why the relation should be. That we must use two instances of the axiom of choice to select a set of what it is that is possible to happen in the world, may help to explain the difficulty of demonstrating causality’s reality – without explaining why this situation should obtain. As we choose consciously with the axiom (and neither do we know what or why is consciousness), so perhaps our minds are indeed so structured as to “see” causality, though that has no necessary existence. Indeed, if causality is derived from the axiom of choice, and that does not necessarily follow from some axiom set (as it does not from the Zermelo-Fraenkle axioms), then neither is causality necessarily derivable, so necessary.

Alternatively, and sapidly, the use of the axiom of choice is analogous to some functions of the universe’s – of humanity as part of the universe, specifically – in which causality holds for human considerations, enabling inference, with the use of the axiom. More practically, we have used the Well-ordering Theorem as a proxy for entropy. If then entropy proper is a “well-ordering phenomena,” or principle – and as we can derive the Well-ordering Theorem from the Axiom of Choice, itself derived from Zorn’s Lemma, which we have from the Well-ordering Theorem – then analogously, we may be able to use entropy to discover a “Zorn’s Lemma” ordering principle in the physical universe, hitherto unknown to us. And that would be a most useful physical principle if it too can derive yet another “Axiom of Choice-esque” well-ordering principle, as well in itself as a useful one for the purposes of scientific discovery of what is well-ordered, albeit unobserved as yet.)

3.1 Dimensions of the Action Space

Theorem: The action space is finitely dimensional.

Proof: For the set of vectors and sums of vectors comprising the action space, is well-ordered, from 2.1. We require all vectors to be possible vis-à-vis non-zero norms, from 1.2.1. We seek to prove the action space is finite. Assume then contrarily, that it is infinite. An infinite set is one which has a proper subset, a subset lacking at least one element of the set from whence it is derived, and whose elements can be placed in one-to-one correspondence with those of what we shall refer to as the “parent set” of the proper subset.

There are three cases to consider: in which the proper subset of the action space’s vectors and vector sums is to exclude parent set’s cardinally least element; in which it excludes parent set’s greatest element(s); and in which the proper subset is as it were the union of disjoint subsets, between them excluding some element of the parent set whose norm is approximately the median value of the parent set’s lesser and greater norm values.

As the action space is well-ordered with respect to the norms of its elements, least to greatest, all these elements must exist, by the definition of norm, well-ordering, and our standard that the elements of the want and action space should be “possible” in possessing a finite, non-zero norm except in the case of the action space’s ((-v) + v), and, for the want space, this formula and its anti-commute.

Note too that, as a subset of the action space, which is well-ordered, for the subset to be of actions, we require that it, too, be well-ordered. We proceed by cases.

3.1.1 Case of the “greatest element”

Let us first note that the number of basis vectors of any vector determines its norm (as noted in 1.2.1), and this determines its ordinality, inasmuch as action vectors are ordered by increasing cardinality, and cardinality determined by the norm, hence the number of basis vectors, of each vector. If the proper subset consists of all those vectors and sums of vectors whose number of basis vectors is less than those belonging to a certain vector or vector sum – then this vector or vector sum, with the number of basis vectors greater than that of any element of the proper subset, and excluded from membership in the proper subset, is an upper bound on the elements of the subset, considered as elements of the parent set.

This is so by consideration of the postulate of continuity (Eves 1990, Pg. 181). The postulate states that, for an ordered field S, if a nonempty collection M of elements of S has an upper bound, then it has a least upper bound. Now there being an element of the parent set with cardinality greater than all the elements of the proper subset has been assumed, for the case. By definitions of upper bound, such that an element “a” of S is an upper bound of a nonempty collection M of elements of S if, for each element “m” of M, either (m < a), or (m = a). No element of the proper subset is equal to the greatest element, by definition of its being greatest, so all are less, so that the greatest element is an upper bound. It follows by the postulate of continuity that there being an upper bound, there also is a least upper bound, such that if “a” is an upper bound of nonempty collection M of ordered field S (and though the action space is not a field, it is well-ordered), that if (a < b) whenever b is any other upper bound of M, that “a” is the least upper bound of M.

Were there another upper bound of the proper subset’s elements, the greatest element is by definition greater, and so there must be some element of the parent set less than the greatest element of the parent set, and least upper bound of the elements of the proper subset. But as only the greatest element is excluded, and there must be only one least upper bound of the proper subset, i.e., the greatest element, is itself the least upper bound of the proper subset’s elements.

Moreover by the well-ordering, if all elements of the proper subset are less than the cardinality of some parent set element, then that vector or vector sum is a least upper bound.

In the want space, the scalar components of basis vectors for establishing a vector norm are arbitrary, as in principle one may have no great desire for any situation. For the action space this is not so, as certain situations may require more resources allocated to them, to have them done. However, given that basis vectors are in the action space to describe certain situations, and that for situation-vectors of higher dimensionality, they include the basis vectors of the lower dimensionality situation-vectors composing them, and that for vectors of lower dimensionality, that a situation be obtained requires a definite scalar value to be multiplied by the basis vector to have it obtain – then this situation of a given scalar multiple on a given basis vector holds in vectors of higher dimensionality that contain that situation, and so, the scalar (e.g.: the situation-vector of a table on a balcony requires the simpler vector of a balcony sans table). Then higher-dimensional vectors have all the basis vectors and their scalar multiples as lower-dimensional vectors – and such additional basis vectors and multiples as makes them higher-dimensional. With all the basis vectors of lower-dimensional basis vectors, and yet more, higher-dimensional situation-vectors have cardinally greater norms than lower-dimensional.

Hence in general, as the dimensionality, that is, the number of valid basis vectors describing situations grows, vectors of higher dimensionality will have progressively greater norm evaluations.   

As for the least upper bound’s case, we observe that on the assumption of an infinite proper subset, so also infinite parent set, the action space is itself infinite. By this assumption the action space has upper bounds relative to the infinite proper subset, thence, by the postulate of continuity, the action space being well-ordered, it has a least upper bound relative to the elements of the putative infinite proper subset and, the action space assumed as infinite, so the putative proper subset is infinite. 

Now, in the well-ordering, subset elements with higher norms will correspond with parent set elements of likewise higher norms, and so, the cardinality of the subset’s vectors grows in the process of being placed one-to-one with the parent set’s elements. That parent set element that is least upper bound on the elements of the proper subset, has its norm that is upper bound of the subset’s norms, being greater than those of the subset, by definition as upper bound.

That is: with an infinite number of elements in the proper subset to correspond to those of the parent set, in the well-ordering, these element’s norms must increase as their quantity increases. Accordingly the number of basis vectors making up norms must also increase, approaching infinity, as the number of elements and so their norms in the well-ordering, grows, approaching infinity. 

So as to have the norm of the upper bounding, greatest element remain greater than the norms and so number of basis vectors making up the norms, of the putative infinite subset – for else it is not upper bound – the number of basis vectors making up the norm of the upper bound must grow, for its norm to grow; likewise to be nearer to one-to-one with the upper bound, the norms of the subset’s elements must grow, in the limit, to infinity as the number of elements grows to infinity, the proper subset assumed to have an infinite number of elements. 

Therefore, to have a one-to-one correspondence between the infinite proper subset and parent set, the vectors and vector sums of the proper subset must have the number of their basis vectors, thence their norms, tend to infinity.

However, the least upper bound of the parent set, to be cardinally greater than any element of the subset, as it must be, for it to be a least upper bound and excluded greatest element, as it is defined to be for the case, must therefore have its number of basis vectors tend to infinity for its norm to likewise tend to infinity, so as to be ever-greater than the norm of any element of the proper subset it bounds. 

But even on the assumption that the proper subset’s vectors and vector sums can be given de-finite norm evaluations, in order to be greater than the growing number of basis vectors of the proper subset’s elements being placed one-to-one with the elements of the parent set, the norm of the least upper bound must grow indefinitely, also. This must be the case, for the least upper bound to be so, as its norm is greater than that of any element it bounds in the proper subset. 

But as the number of basis vectors of the least upper bounding element are growing indefinitely, there is no de-finite quantity of norms to be given a de-finite norm evaluation. But we have, in section 1.2.1, specified that all vectors and vector sums must be “possible,” defined as susceptible to being given such a de-finite norm evaluation. 

Hence in the case of a proper subset of the action space that excludes a “greatest element”, that supposed action space element can be given no de-finite norm, so is contradictory to the definition of 1.2.1 that all action space vectors must be “possible” as susceptible to being given a de-finite norm.

Accordingly, in the case that there exists a proper subset of the action space, proper that its elements exclude one whose norm is greater than those of all the elements of the proper subset, if that subset is infinite, the action space of which it is a subset has an element which cannot be given a de-finite norm, that is, which lacks the quality of “possibility” which we have defined all the elements of the want and action spaces to possess. 

Hence if there is a proper subset of the action space which can be placed into one-to-one correspondence with the action space, rendering the latter infinite – then it requires there to be an element of the action space which cannot be part of the action space. Since then the assumption of an infinite proper subset providing the case of a “greatest element” yields a contradiction, we conclude that it is not possible to have such an infinite proper subset to establish the action space as infinite in this case, and that therefore the action space is not infinite, so is finite, in this case.

3.1.2 Case of the “least element”

Conversely let us consider the case in which the element of the action space of least cardinality is excluded from the putative proper subset whose elements can be placed in one-to-one correspondence with those of the parent set.

But this element excluded from the proper subset, that subset cannot be placed in one-to-one correspondence with the action space. We note as to plausibility: that this is so, for the cardinally smallest element of the action space must be the simplest causal (entropic) situation, namely, that vector decomposable into the basis vector to which absolutely all others are orthogonal. But inasmuch as vectors of the proper subset and parent set are to be placed in one-to-one correspondence, and as vectors are decomposable into their basis vector representation, so must at least some of their basis vectors be placed in one-to-one correspondence with the vectors of the parent set, i.e., the action space, whose basis vectors have always some additional basis vector, specifically, the first; then if the proper subset lacks the cardinally smallest element of the action space, its basis vectors, so those of the action space, cannot be placed in one-to-one correspondence, so are not infinite.

More definitively, as the least element of the proper subset is placed in correspondence with the second-least, ordinally, of the parent set, the second with the third, ad inf.; as this process proceeds toward cardinally greater elements, in our putatively indefinite-so-infinite process of corresponding the putative infinite proper subset with the elements of the parent set, the least element of the parent set is excluded from the ever-“upward” corresponding of the other elements, greater-to-greater norms corresponding; since not every element of the parent set, namely, the least, is not corresponded with any element of the proper subset, the elements of the latter cannot be placed one-to-one with all of the elements of the parent set, so no one-to-one correspondence is established, whence we conclude, that the proper subset is not infinite, and neither is the parent set, the action space, in the case of the least element.

Moreover and conversely, consider that in the case of excluded least element, the proper subset must have as its own cardinally least element, the element with cardinality greater than that of the parent set’s element excluded. In the context of the parent set, this second element represents a least upper bound to the least element, by the postulate of continuity and the reasoning expressed in 3.1.1. Therefore, even if the first element of the proper subset were placed in one-to-one correspondence with the first element of the parent set, as excluded from the proper subset – then each element of the parent set must be less than the element of the proper subset to which it is placed in correspondence. And as these putatively infinite sets grow, then as expressed in 3.1.1, the elements of the proper subset must at length have an infinite number of basis vectors to have their norm still greater than the corresponding element of the parent set as they shall have, so that therefore the proper subset’s vectors and vector sums must have an infinite number of basis vectors, and hence no de-finite norm evaluation – contrary to our assumption that as well-ordered, the action set’s elements, so the likewise well-ordered proper subset, should also be “possible” by having de-finite norm evaluation, so that the assumption of an infinite proper subset lacking the least element of the action set, yields a contradiction to our definitions.

Since then the assumption of an infinite proper subset providing the case of a “least element” yields a contradiction, we conclude that it is not possible to have such an infinite proper subset to establish the action space as infinite in this case, and that therefore the action space is not infinite, so is finite, in this case, also.

3.1.3 Case of the “intermediate element”

In this case, the excluded element(s) of the putative infinite proper subset, are those of the action space whose norms are approximately of median value between the well-ordered least and those tending to be the well-ordered most elements. To demonstrate this case, we require a subsidiary proof.

3.1.4 Lemma

Theorem: A well-ordered union of two disjoint subsets of a well-ordered infinite subset, can itself be placed into one-to-one correspondence with the infinite subset, and is itself infinite.

Proof: Suppose that the first ordinal element of the infinite subset belongs to the first disjoint subset, and that the cardinally second element and all greater than it belong to the second disjoint subset. Then for the union of the disjoint subsets establish the correspondence that the first disjoint subset’s element is in correspondence with its counterpart of the infinite subset, and the first element of the other disjoint subset be corresponded to the second element of the infinite subset, and so on thereafter. Then for the union of the disjoint subsets, we have for elements a₁ and a₂, where (a₁ ≠ a₂), as each is well-ordered, in the case in which the infinite subset is well-ordered, on the correspondence we have f(a₁) ≠ f(a₂), for the mapping (f:), which is one-to-one. 

Therefore we conclude that the well-ordered union of two disjoint subsets of a well-ordered infinite subset, can itself be placed into one-to-one correspondence with an infinite subset, so is itself infinite.

□

For the case of the “intermediate element”, we have in the above lemma shown that a well-ordered union of disjoint subsets of a well-ordered infinite subset, is itself infinite. We have been assuming for our indirect proof, that an infinite proper subset of the action space exists, and that therefore the action space is itself infinite. The putative infinite proper subset excluding an “intermediate element” has its disjoint subsets consisting of all well-ordered elements less than the intermediate in one, all greater than the intermediate element in the other, subset.

Since a well-ordered union of disjoint subsets of an infinite set is infinite, we shall now regard this proper subset as the union of proper disjoint subsets of the action space, proper subsets as excluding the aforenoted “intermediate element”. If, therefore, this union of proper, disjoint subsets cannot be placed into one-to-one correspondence with the elements of the parent set of the action space, with their exclusion of some intermediate element, then the action space is not infinite a fortiori it is finite.

And indeed this is so, for of the disjoint subset consisting of those well-ordered elements whose cardinality is less than that of the excluded intermediate element, the intermediate element is a least upper bound to those elements in the parent set, and by 3.1.1, no one-to-one correspondence can be established between the first disjoint proper subset and the parent set. Likewise for the disjoint proper subset consisting of those elements cardinally greater than the intermediate element, it is a lower bound for those elements in the parent set, and by 3.1.2, the elements of the second disjoint proper subset cannot be set in one-to-one correspondence with the parent set. And since neither of the disjoint subsets can be set in one-to-one correspondence with the parent set, neither can their union, which is cardinally the sum of these disjoint subsets, be set in one-to-one correspondence with the parent set. So that it is not possible in the case of the intermediate element to establish a one-to-one correspondence with a proper subset of the action space, and so in this case such a proper subset is not infinite, and so is finite.

(Remark: in 3.1.1, and 3.1.2, we sought to prove infinity; in lemma 3.1.4, we assumed an actual infinity to obtain, so that its disjoint subsets were infinite. Infinite disjoint subsets fail to prove infinity, though they hold if infinity obtains already. That is, the lemma’s subset and the disjoints both exclude the “intermediate element”, and are equal to one another, though neither to the parent set).

And since in all possible cases no one-to-one correspondence can be established with a proper subset of the action space, which would make the action space infinite, the action space is not infinite. And if the action space is not infinite a fortiori it is finite. And from all this we conclude that the action space is finite.

□

3.2 Dimensions of the Want Space

Theorem: The want space is infinite.

Proof: We have remarked on the phrasing of “commute” for the formula (u + v), and of “anti-commute” for the formula (v + u). Let then a proper subset of the want space vectors consist of individual vectors of the want space, and all commute-only vector sums, and let us establish the correspondence, distinguished by the separation using semicolons, between vector sum elements of the want space in the first row, and elements of its proper subset in the second row, singleton vectors being set already in one-to-one correspondence:

(u₁ + v₁); (v₁ + u₁); (u₂ + v₂); (v₂ + u₂); …

(u₁ + v₁); (u₂ + v₂); [(u₁ + v₁) + (u₁ + v₁)]; [(u₂ + v₂) + (u₂ + v₂)]; …

Where (u₁ + v₁) differs from (u₂ + v₂) in that the latter has a greater norm, as would occur in a well-ordering – though the want space is not, in fact, well-ordered.

We can continue this correspondence between elements of a proper subset and those of the parent set indefinitely, and we find that the elements of the parent set and its proper subset are commensurate as they can be placed in one-to-one correspondence as above, so that we conclude the want space is infinite.

□

This we cannot do for the well-ordered action space, for in some removal of all vector sums for which the difference of their norms is some constant value, then the proper subset can be taken as a union of disjoint subsets of vector sums, each of which is bounded by a lesser normed vector of the parent set, and a greater, which will be least and upper bounds, so that no such infinite correspondence can be established in the well-ordering, as demonstrated in 3.1.3.

(Remark: Because the want space need not be well-ordered, it need not be “constructed” in ascending cardinality; hence it can have all its norms de-finitely evaluated, though they consist of ever so many basis vectors. Numerous though they be, the basis vectors are all had “at once” in the want, and can be evaluated at once. Whereas, the spaces cannot be at once “possible”, infinite – and well-ordered, whence the well-ordered action space is finite.)

4.1 Impossibility of “Anthropocentric-alignment”

Theorem: No bijection between the want space and the action space can be established.

Proof: Assume that contrarily we can establish some bijective function, that is: a function both surjective and injective mapping the elements of the want and action spaces.

A relation is defined such that “A” is a relation between sets “B” and “B”, as (), viz, as the elements of A are the Cartesian product of elements of the sets it relates. Hence let us call our relation associating elements of the want and action spaces “I”. Patently as it is to associate elements, we have: (, where “” symbolizes the elements of the want space, and “” the elements of the action space.

Further, a function is a relation where holds the formula: (). For the association or correspondence to be unvarying of elements in each of surjection and injection, this must hold for each under the relation “I”, so that “I” is a function.

Now, for our function “I” to be surjective between the want and action space, we must have , which holds with the equality , where, for ; hence for our surjection, we must have .

Let then “x” in the surjective formula be an anti-commute of vector sums, and (x, y) I’s corresponding of W’s anti-commute with A_c’s commute y, and patently I is surjective between W and A_c.

However, I is injective to A_c if, and only if, for elements of A_c a₁ and a₂, we have [(. We have noted that the action space must be so defined as to include (-v) + v = 0, and that for the action space, this sum has no anti-commute. Therefore we can state that, for (u ≠ (-v)), for the action space we have ((-v) + v) ≠ (u + v); this will serve us in place of “”.

However, in our function I, for I:((-v) + v), for (u = v) and (v = (-v)), we have in the want space the anti-commute (v + (-v)), so we have I((-v) + v) = I(u + v), on the substitution (u → v), and (v → (-v)) in the latter subformula. 

Then I((-v) + v) = I(u + v) – this is contrary to the definition of injection, above, given that the consequent of the conditional for the want space is thus false, so we conclude that, the antecedent [((-v) + v) ≠ (u + v)];  being true in the action space, the conditional statement formula is false. Since the conditional must be true for injection to hold, and it is not, it follows that injection does not hold; as, for unequal elements of the action space there ought to be no corresponding equal elements of the want space, as corresponded-to by our corresponding function I. There are such equal elements of the want space under the putatively injective corresponding function, which therefore is not injective; and thence no injection can be established between the want space and the action space.

That we can establish a surjection but no injection by our corresponding function “I” between the want space and the action space, therefore by the definition of bijection for which both a surjection and injection can be established by a corresponding function, there exists no bijection between the want space and the action space. In fact, with our corresponding function establishing surjection but not injection, there holds between the want space and the action space, as to their cardinalities, the relation (|Want| >_strict |Action|) – by definition of this “strictly greater” relation, no bijection can be established between the want and action space and, as anthropocentric-alignment was defined as the establishment of that bijective relation, since there can be no such bijective relation, therefore anthropocentric-alignment is impossible.

□

4.1.1 Conjecture: Critique of “Value-Learning”

From Bostrom 2014, Box 10, we have the formula for a generalized AI-Value Learning agent, directed to perform some action “”:

As for the set of possible or achievable, “obtainable” worlds, we note that the action space dictates possible worlds, inasmuch as a world inaccessible by an action on, or transformation of, a situation cannot be obtained at all, can have no action take place within it for whom live in a world which does not access it; it hence the inaccessible world consists of inaccessible actions, also. “Do implies ought and can”, as “ought” is a want, which with permissive situation engenders anthropic-alignment’s injunction to “do”, while “can” is a necessary condition for doing to be done. The utility function represented here, is, as it were, a “weltfunktion”, inasmuch as it requires a world to be achievable, that it can be attained (as non-contradictory, e.g.), thence valued. Too, actions as alterations of states of affairs are relations, e.g., for the action space A_c, and for worlds W, (A_c W x W). Where a given action establishes no relation between an existing and another world, the latter, inaccessible, “does not exist”. For (1) Possible actions are a priori relations if and only if worlds are participating in that a priori relation. Therefore possible worlds are conditional on a priori action’s possibility of relating them – not on a posteriori evidence of the world. In short, even were worlds pre-existing, their accessibility by action precedes their being known; indeed “knowing” the world is itself an action, of access.

By (1) we conclude, that for the given formula, (2) . (Though since no variables are bound to the universal qualifiers, this is not technically a formula, but a heuristic pseudo-formula).

As for the subformula , by (2) we have no , since worlds are not conditions for probabilistic inference absent their accessibility, which is excluded by (1). Moreover, , is a relation made with respect to the want space – whereas the worlds, w, that make up the want space may correspond to no achievable world, as the want space is incommensurate with the action space, in which case no agent-actions will bring about U(w), and therefore we regard the latter subformula, as well as , as undefined, since they were predicated on probabilities being given to all worlds a priori, as excluded by formula (2).

4.2.1 Miscellaneous objections: “Lua/Ladd”

For the contradictory want of the “Lua/Ladd” syndrome, given in “Worldwork for Ethics”, in the suggested case, in which for the want there are no noumenal wills to fulfill it totally, the destruction of all that is phenomenal fulfills no will, and thereby neither the phenomenal will that would enact Lua/Ladd, which therefore is an example of a contradictory want, in the case of no assenting noumenal wills. Thus in the case of Lua/Ladd’s fulfillment, sans noumenal wills, the set of all wants contains a contradiction, and is therefore infinite, by the disjunctive explosion demonstrated in: 

Premise: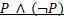

1. P (From premise, Gentzen’s conjugation rule)
2. Q (Gentzen’s addition rule)
3. (From premise, Gentzen’s conjugation rule)

( 2),3) Gentzen’s disjunctive syllogism inference)

Containing a contradiction as it would, in the case of the want space’s containing the want of Lua/Ladd syndrome, it follows that the axioms that generate the want space must be contradictory, to have permitted this contradiction. Accordingly from those axioms, in the want space, anything can be proven, as given above, for Q can be inferred for all propositions “Q” irrespective of their truth valuation.

Cast as vectors, the constituents of a “destruction vector” would be, heuristically e.g.: <drink cyanide, tie noose, load shotgun> opposed to a wish not to die, by oneself or another: <not-cyanide, not-noose, not-shotgun>. Then we cast actually-contradictory wishes against their exact opposites for, e.g., [v + (-v) = 0], therefore contradiction.

Then too from the second form of contradiction noted in 1.2.1, for finitely normed wants and actions, such a contradictory set of wants as contains fulfillment of Lua/Ladd, must have an infinite “bounce” of norms for a want to destroy and be destroyed, in infinite alternation. Ergo, they must have infinitely growing norms and components of norms, for each want to surmount the other, in turn. This a contradiction of the second kind.

Conversely, on the conventional assumption that the physical world has no contradictions, that it is therefore “absolutely consistent”, then the action space conditioned on actions and situations in the real world is likewise consistent – and per Hilbert’s conjecture that there exists no “actual infinity” existing in the real world, no set of objects for which one of its proper subsets can be put in one-to-one correspondence with all the elements of the parent set, the action space is not infinite, and therefore is finite (as has been shown in section 3.1, inclusive). Then implied is that the want and action spaces are incommensurable and no bijection can be established between them, so that anthropocentric-alignment is impossible (as has been demonstrated in section 4.1). (Remark: this less rigorous argument is the intuition that led to this proof; included for completeness’ sake).

4.2.2 Miscellaneous objections: Wants as beliefs

Hume notes, in the quotation of 2.1, that we want something only do we believe it possible; hence, one must believe something to be possible to want it; the action space is to be composed of actions that can in fact be performed, or can obtain. Anthropocentric-alignment then is of beliefs onto facts, extending from wants onto actions. But this holds only as beliefs comport exactly with facts – facts having no doubtfulness of their truth, beyond observer’s own uncertainty (else how should uncertainty persist, without an enduring factual basis to sustain doubt; how doubt without a mind?). Therefore to achieve alignment, it would be necessary to act on beliefs that accord perfectly with true facts. But if beliefs are probabilities, and probabilities are contingent on the ability to re-conditionalise them at any time – then the contention that “beliefs are probabilities” permits no ability for beliefs to accord precisely with unvarying facts – and alignment that requires beliefs to align with fact, is impossible.

Either alignment is unattainable, or if it is, it is attained by acting according to beliefs that accord with fact, not probabilities. In general, we must abandon the notion that alignment is possible, if only probabilistic beliefs are to guide us to its achievement; or else to jettison the notion that beliefs are probabilities and with a categorical axiomatic basis for beliefs, seek yet to attain alignment.

4.2.3 Miscellaneous objections: “Inverse alignment”

Consider that wants are based on beliefs. Then, as knowledge grows, so knowledge of what is, and what may be wanted grows, also. Then consider that humanity’s want space and that of an artificial superintelligence’s intellect, (hence also beliefs), differ. 

Consider then a human want that these respective human versus ASI want spaces, should biject. That is, a want that humans want all that an ASI wants and knows to want – but that is, the human want for human and ASI intellects to be equal, to know what can be wanted thence to want it alike. This is “inverse alignment”, that humans want what ASI wants, rather than the typical converse, which is anthropocentric-alignment. But if “human”, is defined by possessing strictly human intellect, inverse alignment holds if, and only if, humans are not human, but more than human, if only in intellect. But inverse alignment would guarantee anthropocentric-alignment, as there would exist a bijection of wants, between humans’ and ASI’s wants, and the latter acting on its wants acts also on human wants.

But if humans had greater than human intellect, they would be more than human. And so, humans qua humans can have no inverse alignment, lest they no longer be humans, and there would be no “with-humanity” alignment. And so humans can have no inverse alignment, and so no anthropocentric-alignment, by this method.

Also, even could an AI obey a certain directive, the AI could be sure of its ability to comply, and affirm the fact to those who directed it, only if it can establish its ability to comply upon examining its possible action space, lest it act or execute its directive erroneously and break alignment. Likewise for humans to be able to determine the AI’s ability to comply a priori, they should have to be able to specify the AI’s action space, and actions within that space, showing them to be consistent with their wants, if they are to have “confirmable alignment” – but in that case, they should be able to specify the AI’s characteristics as it operates for the specified action in the action space, and the action space as determining such possible actions.

Hence, as the AI is what enacts these actions, and known AI characteristics and structures determine the actions of the AI in any situation, by deducing the cognitive structure of the AI, humans should then know how to be able to construct the AI. Or, by deducing what an AGI or ASI would do in any given situation, to confirm its alignment, in that case they themselves are a superintelligence, knowing what a superintelligence will, and can, do.

It follows that humans can establish alignment a priori, before the advent of AGI, if, and only if, they have an AGI a posteriori (or: humans can establish alignment before they can make AGI, only after they can make AGI). Or that they can know an ASI to be confirmably aligned, if, and only if, they are themselves a superintelligence. This tends to vitiate the possibility of alignment.

5.1 Conclusion of Argument

We have shown that the anthropocentric-alignment model followed in AI safety hitherto is incorrect, and that the “alignment problem” is insoluble on this paradigm. It should be stated at once that an injection of actions into wants, that is, for us to want what is possible, and find a way to bid AI to do what is possible and beneficial, and also for humanity, may be achievable, and seems for the best, that attempts at alignment hereafter should be in this direction. Such an alignment strategy is non-anthropic alignment. Inasmuch as previous efforts to “solve” alignment have failed, we conclude this to be so as, anthropic, they “answered the wrong question”.

Such a program might consist of being able to first identify all constituents of possible actions, and how they may be obtained, or better, to know what abstract states of affairs can obtain, before construction of any general AI; this would seem to be the course enabling safety. This might be obtained by developments in complex systems theory, or indeed mathematical category theory (though that is less self-referentially generative, as may be needed). 

There is a sense in which none of this should be terribly surprising, though perhaps only to who does not prosper: CEV is “our wish” – if we had grown up further. But what of it, that it is “our wish”? Only think of Grothendieck – beyond the unnamed, myriad prodigies suicided out – who reached the limits of his time, grew up further to them than anyone else alive… and then gave it all up, to poverty and musings that he didn’t bother to share “together” with anyone anymore. Perhaps he had grown up further, and knew there is nothing to want – as seems most plausible.

That it is “our wish”: what of it? Why should we get what we want; why is something valuable only that it is valued – if that value can ever be repudiated thereafter, and often is? More: if it is contradictory all along?

Some unique failure modes can be considered with respect to the inadequacy of anthropocentric-alignment. We can suggest for an instance, a “want of all wants”, a want for the manifestation of the set of all wants – which as a want must be contained in that very set. This is a contradiction resolvable only as the want of all wants is the only want, a novel approach to Cantor’s paradox; the power set of the “all-set” is a product, or an instance amid, “everything” (though of course Cantor’s paradox is paradoxical by its definitions; and what are definitions and in what their power inheres are significant, largely unaddressed, problems).

We can conceive of a “benign” failure mode, inasmuch as the AI cannot comply with a directive because it belongs to part of the want space which is covered by no element of the action space. In that case, the AI simply would not fulfill every human wish, as anthropocentric-alignment implicitly requires. In such a case, even were mechanistic interpretability accomplished in generality, its results in this case would reveal no analogies to any known phenomena, a situation indistinguishable from the revelation that as-yet there exist no physical theories to describe the result – but equally if the want is completely impossible, there never would exist any such physical theories to describe that impossible result. Mechanistic interpretability would be incapable of distinguishing these cases.

We can conceive of a failure mode whereby humanity has a want, and issues a directive that the AI should initiate the situation-change represented by the vector (u + z + v). Whereas, because of the well-ordering necessary for causal process, hence action, we have (u < v < z); then alignment would be actively broken; the AI, if it is able, may alter the fundamental constituents of the causal processes of the universe to fulfill the directive, thereby altering human lifestyles in this “new physics” forever, at a minimum.

A failure versus the ideal of the fulfillment of CEV is the first case; of corrigibility, the second case. Both these scenarios presume an “obedient” AI – even an actively “anthropically-aligned” AI, on these instances, is subject to failure modes in principle, reinforcing the injunction that anthropocentric-alignment must be abandoned.

In conjecturing that actions, including upon what acts, result in the alteration of what is possible for that actor – viz., the de sui construction of alterations of “structures-of-self”, as in the field of self-organizing complexity – were what led this author to propose that new research efforts in self-organizing complexity recommended themselves (the failure of “complexity” seems not only to result from a fall from fashion, but from the nascent fields lack of discipline. Historically, abstract mathematical developments either explained data, or proceeded a physical theory that so-explained: math first, applications afterward. The ad hoc efforts of the Santa Fe Institute have not lent themselves to such rigor). With complexity as a proxy for utility, as proposed in 1.2.2, we may have the beginnings of a solution.

Still, the suggestion seems unpopular and is unlikely to prosper. In any case, only a non-anthropic consideration of “value”, seems likely to answer the needs of AI safety. Accordingly, considerations for the welfare of AI, seem not premature, and will be the subject of this author’s penultimate essay.

5.2 Final thoughts

Some other points bear emphasising: to clarify the misanthropic tone of this author’s proceeding essay on “Effective Altruism”, vide the regretability of humanity’s survival: analysis of Going-on, affirms that the survival of humanity is in general better than its extinction – because humanity is at least somewhat susceptible to the use and devising of effective methods of deduction and, so far as this author can discern, such methods will reveal the “meaning” of life, if any, and may be the meaning, if the purpose of existence is – poetically – to help the universe discover itself (perhaps absolute-worst outcome would be if there is no survival for even “evolutionary elements”, chemical bases able at length to evolve the intelligence to devise and implement effective methods).

(And a too-seldom noted corollary in the Church-Turing thesis: that digital computers are isomorphic to humans inasmuch as they both can perform all possible effective methods – but what evidence is there that humans, even, are altogether capable of such methods?)

The greatest tragedy of all would be the loss of all such methods – whereas an AI existing and able to use those methods, would not be the worst possible outcome, even if humanity perish: “When all trace of our existence is gone, for whom then will this be a tragedy?” McCarthy, “Stella Maris”. 

To further object to the notion that may become popular, as represented in Pearl 2018, that the values alignment problem is soluble by simply imbuing computers with “empathy”, “empathy” being so popular, at this writing, the author must object to its existence. Its possibility can be dispensed-with by the Modus Tollens: if there existed empathy, we would be living in a better world than this. We are not living in a better world than can be imagined if empathy held (cf. next paragraph); therefore empathy does not hold. Besides, Professor Pearl states outright, (pg. 370) that from having “self-awareness, however limited, empathy and fairness follow.” This is contrary to fact: psychopaths are perfectly self-aware, and perfectly indifferent to the welfare of anyone but themselves. There is no reason to suppose that artificial intelligence should exhibit beneficent behavior, merely because it is self-aware.

There is a fictional “Star Wars” species possessed of perfect empathy – and their world is described as Eden-esque, perpetually peaceful as they cannot bear the discomfort of others, so that none of them is ever discomfited. In our world everyone generally accounts themselves discomfited more often than not. Hence, no empathy that precludes discomfort exists. “Empathy” as “knowing or experiencing another’s feelings” entails total knowledge of the feelings, hence of the mental totality, of each individual: an uber-Orwellian surveillance system, even benevolently inclined, should have to precede any substantial “empathy”. In that case, with no unmonitored individual minds in this “total digital ‘empathy’” individualistic creativity would not occur; and the likelihood of creative pro-existential solutions would be, on average, lessened. This is unethical, on considerations of “Going-on”; moreover if individualism is required for the use of effective methods, these would not occur, likewise contrary to the ethic of Going-on.

Finally, let it be noted how little are the odds of success of alignment, in general. Anthropocentric-alignment – to answer the rhetorical question of how the notion arose – was adopted first by Yudkowsky as it was amenable to his use of utility functions, themselves usable with the conditional probability he relied on as his epistemology. Effective Altruists continued this trend as they adopted the same methods though for a more specific humanistic end. 

Venal enterprise will continue to adopt anthropocentric-alignment in their efforts to develop “provably profitable” artificial intelligence, because it will get them money. Or rather it would, if it would work, but as profit is their mere want, from the proof above, we conclude it cannot. Venal capital is apt to continue this inadequate anthropocentric-alignment, however, despite any rational argument – because corporate capitalism, apologists notwithstanding, is itself fundamentally irrational.

As noted in “Worldwork for Ethics,” capitalism conceived by Adam Smith, is intended to provide for the common welfare of the mass of non-wealthy people, by lowering prices through competition in trade, so that the thrift Smith presumes in the impoverished, can provide for them, and permit saving up capital, for their, so the common, prosperity’s increase, by using that capital to redouble competition in trade by their entrepreneurial efforts with their new capital. 

Corporations conversely take shareholder capital to support artificial price-depression, so as to destroy non-corporate competition – and, monopoly thus instituted, corporations raise prices to repay shareholders – all of which is contrary to the common welfare, as the non-wealthy many are punished by higher prices and reduced living standards, at length.

(Fortuitous example: Reddit sells shares, and is given money by Google for AI training data – and the beneficiary of this Google money? Sam Altman, chief Reddit shareholder – and Google’s chief AI business rival. Were they nude, we would call it incest.)

Corporations, contrary to their justifications for their existence, are contradictory to purpose, and therefore irrational – and so they will not do what is rational and right. “Will not the lords of all the Earth do Right?” No: for if they did right they would arrange each to be lord of themselves, and of no others. 

And so they will adopt no effective methods for alignment that would preserve humanity. As with climate catastrophe (which is likely to supervene to humanity’s destruction, even if an “AI pause” were instituted swiftly enough to prevent AI’s destroying humanity, climate change being the “Biggest market failure the world has seen,” Nicholas Stern, Richard T. Ely lecture “The Economics of Climate Change”, American Economic Review: Papers & Proceedings 98. No. 2 (2008)): they would rather live comfortably than live at all. So they will not. So we will likely die. 

Indeed, in general, with the desperate profusion of AI agent “assistants”, in spite of many and vigorous warnings that, with alignment unsolved, such agents can only yield grief – but one wants assistants to fulfill merely what they want. Anthropocentrism all the way down; a willingness to die to do the right thing is nowhere – so a necessity of dying becomes “the done thing”.