This is a relatively clean subproblem that we came upon a few months ago while thinking about gradient hacking. We're throwing it out to the world to see if anyone can make progress.
Problem: Construct a gradient hacker (definition below), or prove that one cannot exist under the given conditions.
Setup: Let be the network inputs, , be the network trainable parameters, be the network outputs, and be the network architecture. must be a feedforward neural network that reads in its own weights as input. Weight sharing is allowed (vertical or horizontal), and some weight sharing is necessary in order to take all w weights as input.
Suppose that we train this network on a dataset , with MSE loss , assuming gradient flows: . Given an initial point , the training dynamics are therefore:
Definition: A tuple is a gradient hacker if the following conditions hold:
- is not a global optimum: such that
- such that :
- the network’s training converges to , i.e., .
- There is internal structure of that computes the gradient; i.e., there is some subset of the activations whose mean over every datapoint in D is . [1]
This captures my intuition that a gradient hacker knows where it wants to go (in this case "get to "), and then it should decide what it outputs in order to make the gradient true.
Some more ambitious problems (if gradient hackers exist):
- Characterize the set of all gradient hackers.
- Show that they all must satisfy some property.
- Construct gradient hackers for arbitrarily large , , , and neural net depth.
- Variations on the problem: a subset of the activations equals for every input, or the subset of activations correspond to the gradient on that input.
- ^
This is a bit strict, but we didn't want to list different ways something could be isomorphic to the gradient.
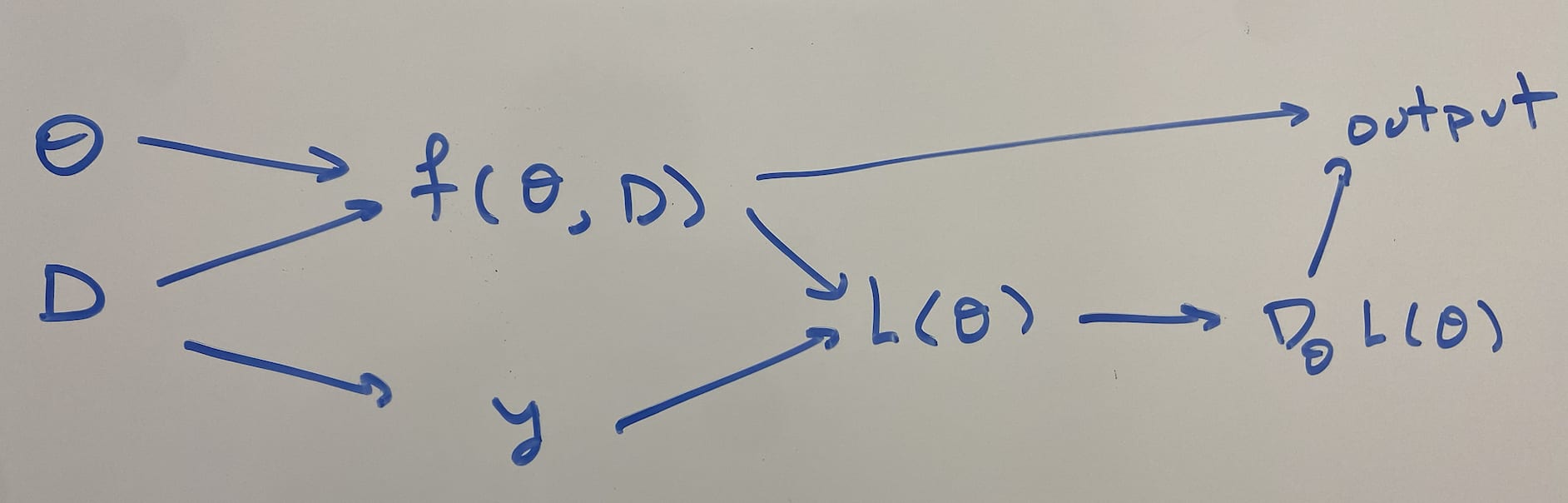
This is very interesting and I'll have a crack. I have an intuition that two restrictions are too strong, and a proof in either direction will exploit them without telling you much about real gradient hackers:
If I understand this correctly the weight restrictions needed mean θ actually lives on a d dimensional subspace of Rw. My intuition is that in real life the scenarios we expect gradient hackers to get clues to their parameters but not necessarily a full summary.
In a reality maybe the information would be clues that the model can gleam from it's own behaviour about how it's being changed. Perhaps this is some low dimensional summary of it's functional behaviour on a variety of inputs?
I think the phenomena should not be viewed in parameter space, but function space although I do anticipate that makes this problem harder.
Instead of expecting the gradient hacker to move toward the single point θg, it is more appropriate to expect it to move towards the set of parameters that correspond to the same function (if such redundancy exists).
Secondly, I'm unsure but If the model is exhibiting gradient hacking behaviour, does that necessarily mean it tends toward a single point in function space. Perhaps the selections pressures would focus on some capabilities (such as the capacity to gradient hack) and not preserve others.
Epistemics: Off the cuff. Second point about preserving capabilities seems broadly correct but a bit too wide for what you're aiming to actually achieve here.