I look at graphs like these (From the GPT-3 paper), and I wonder where human-level is:
Gwern seems to have the answer here:
GPT-2-1.5b had a cross-entropy validation loss of ~3.3 (based on the perplexity of ~10 in Figure 4, and ). GPT-3 halved that loss to ~1.73 judging from Brown et al 2020 and using the scaling formula (). For a hypothetical GPT-4, if the scaling curve continues for another 3 orders or so of compute (100–1000×) before crossing over and hitting harder diminishing returns, the cross-entropy loss will drop, using to ~1.24 ().
If GPT-3 gained so much meta-learning and world knowledge by dropping its absolute loss ~50% when starting from GPT-2’s near-human level, what capabilities would another ~30% improvement over GPT-3 gain? What would a drop to ≤1, perhaps using wider context windows or recurrency, gain?
So, am I right in thinking that if someone took random internet text and fed it to me word by word and asked me to predict the next word, I'd do about as well as GPT-2 and significantly worse than GPT-3? If so, this actually lengthens my timelines a bit.
(Thanks to Alexander Lyzhov for answering this question in conversation)
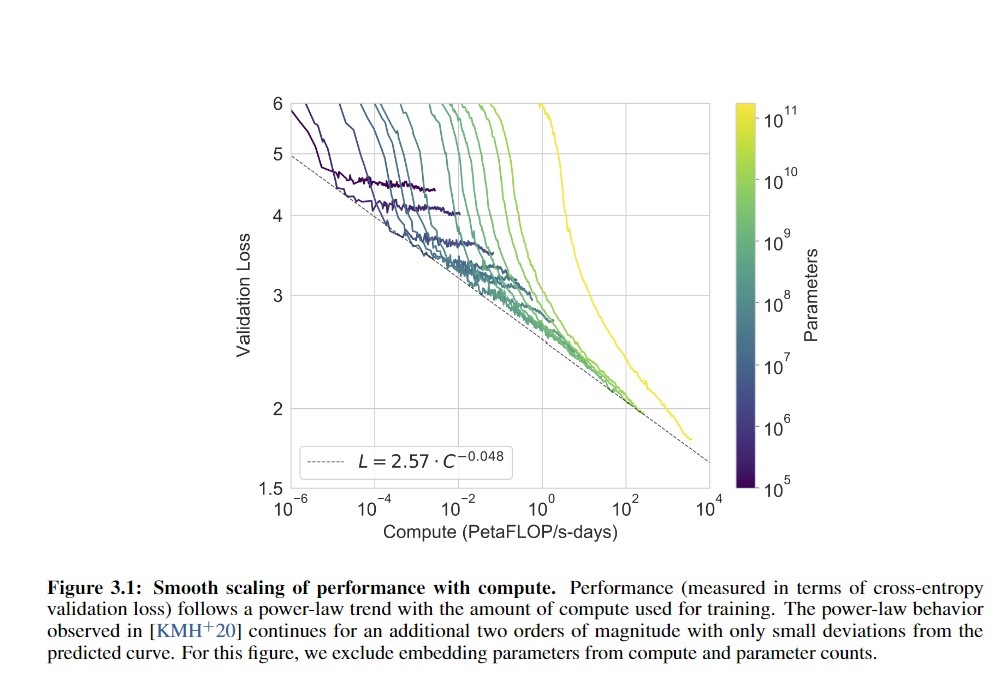
It's probably a lower bound. These datasets tend to be fairly narrow by design. I'd guess it's more than 2x across all domains globally. And cutting the absolute loss by 50% will be quite difficult. Even increasing the compute by 1000x only gets you about half that under the best-case scenario... Let's see, to continue my WebText crossentropy example, 1000x reduces the loss by about a third, so if you want to halve it (we'll assume that's about the distance to human performance on WebText) from 1.73 to 0.86, you'd need
(2.57 * (3.64 * (10^3 * x))^(-0.048)) = 0.86where x = 2.2e6 or 2,200,000x the compute of GPT-3. Getting 2.2 million times more compute than GPT-3 is quite an ask over the next decade or two.