You assume the conclusion:
A lot of the AI alignment success seems to me stem from the question of whether the problem is easy or not, and is not very elastic to human effort.
AI races are bad because they select for contestants that put in less alignment effort.
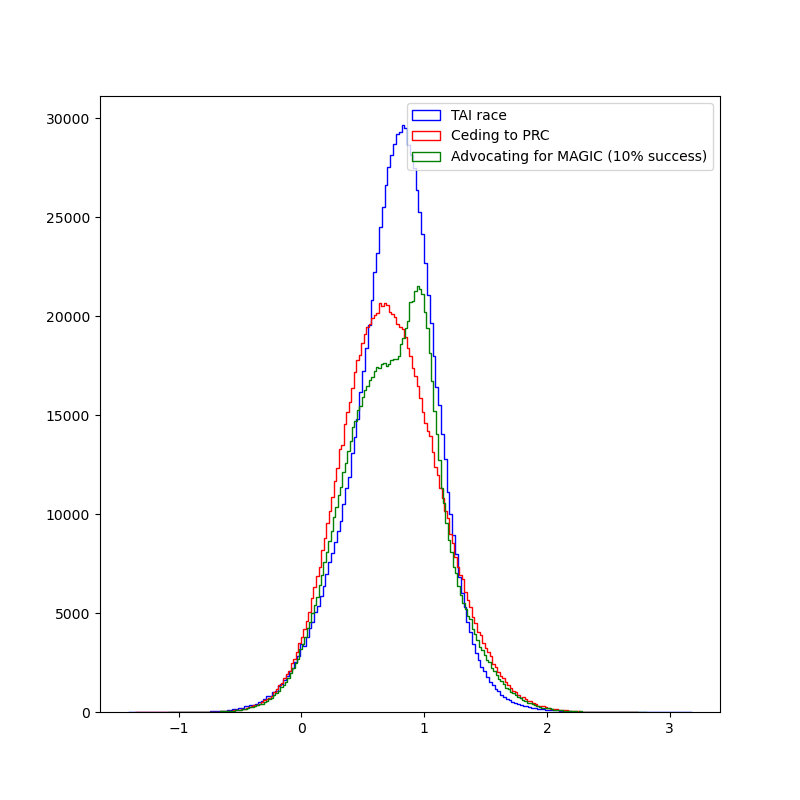
I do assume that not being in a race lowers the probability of doom by 5%, and that MAGIC can lower it by more than two shannon (from 10% to 2%).
Maybe it was a mistake of mine to put the elasticity front and center, since this is actually quite elastic.
I guess it could be more elastic than that, but my intuition is skeptical.
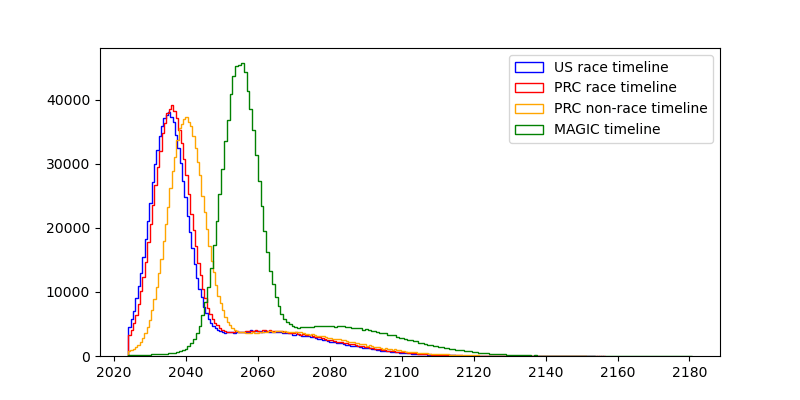
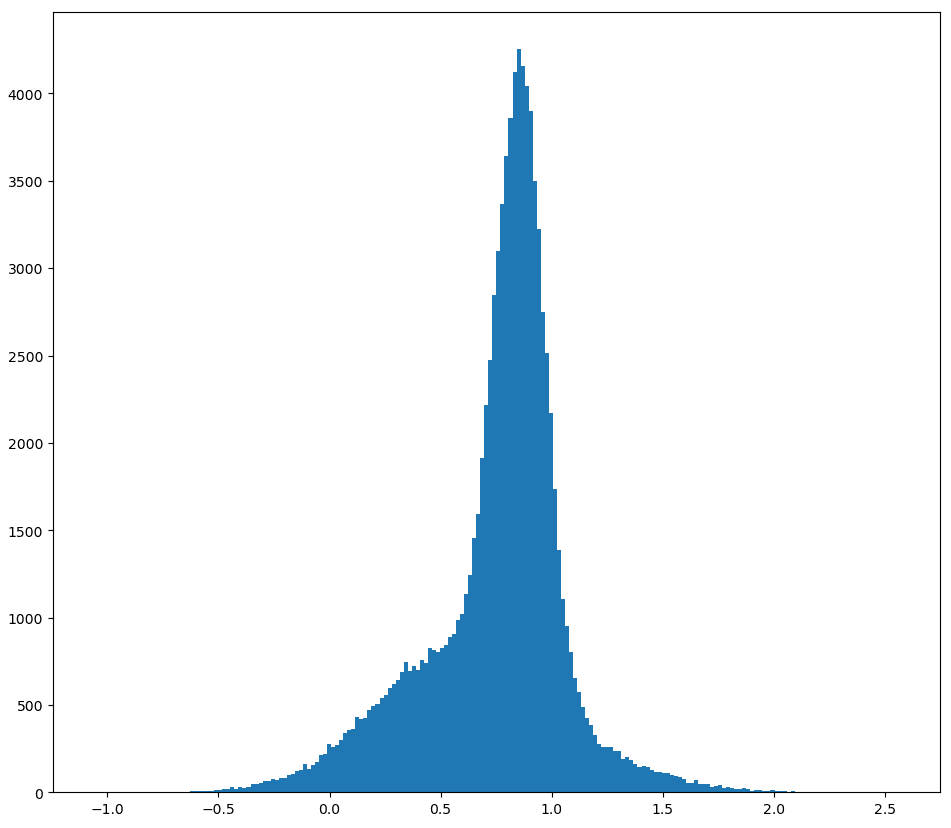
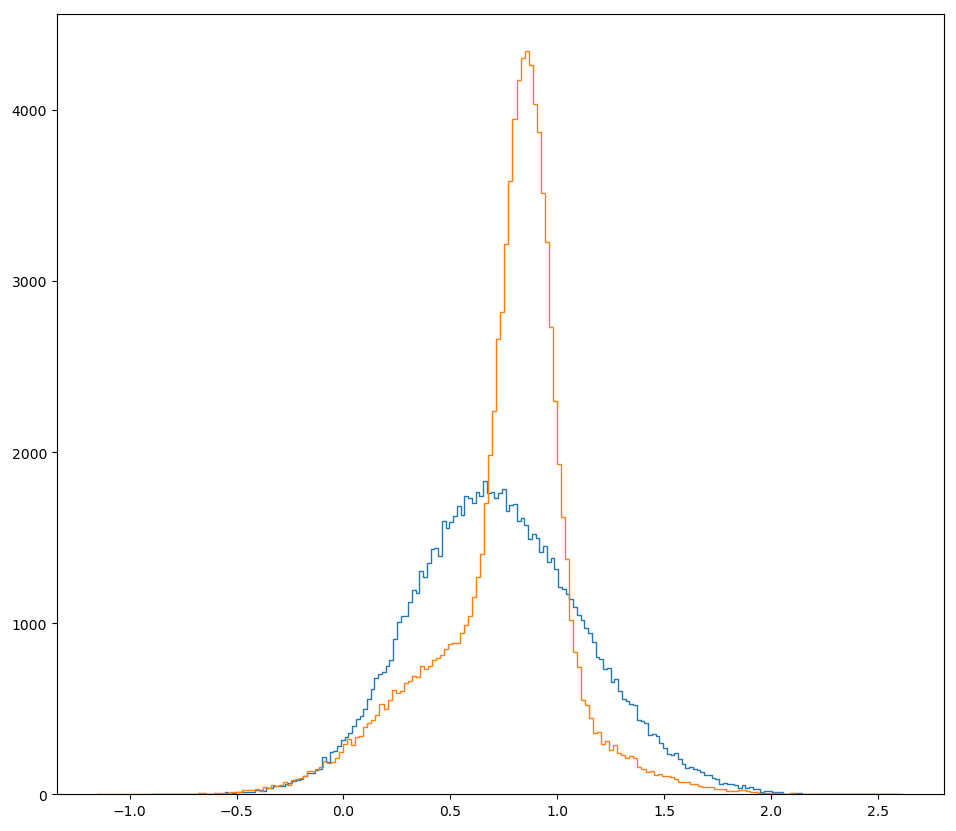
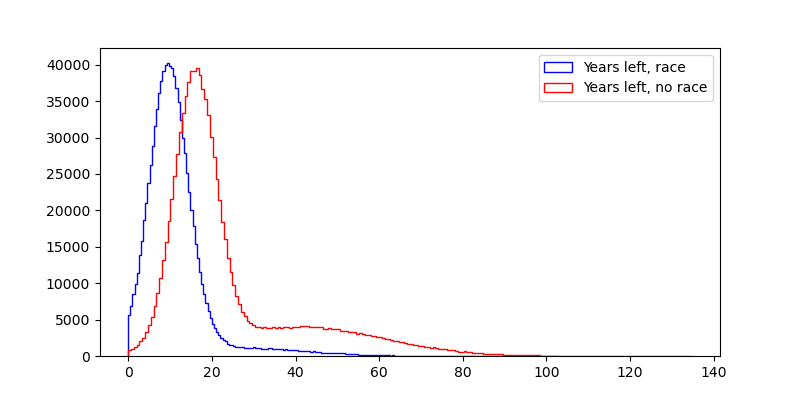
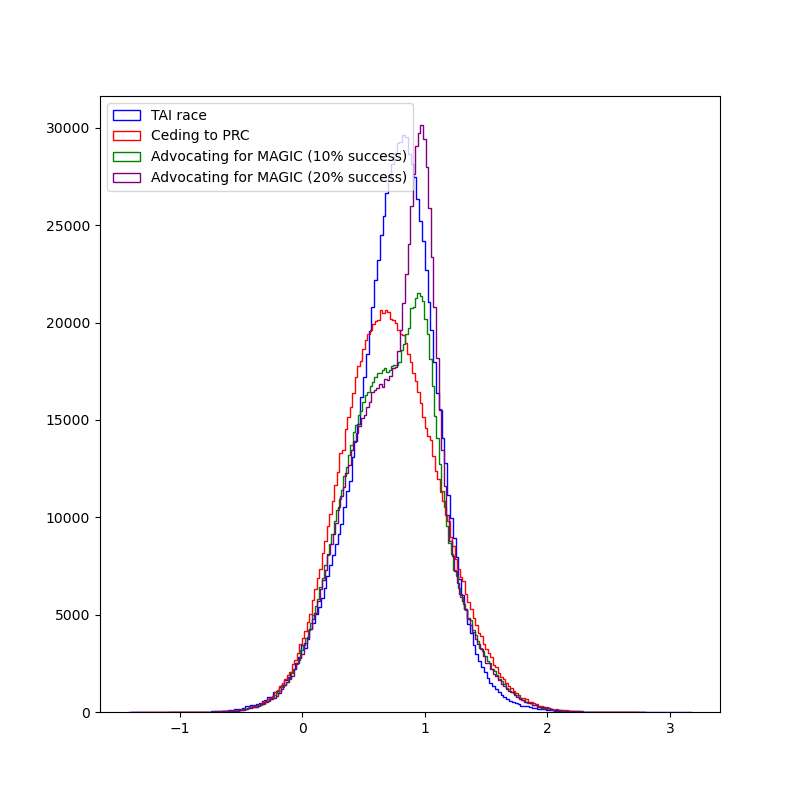
I'm confused by this graph. Why is there no US non-race timeline? Or is that supposed to be MAGIC? If so, why is it so much farther behind than the PRC non-race timeline?
Also, the US race and PRC race shouldn't be independent distributions. A still inaccurate but better model would be to use the same distribution for USA and then have PRC be e.g. 1 year behind +/- some normally distributed noise with mean 0 and SD 1 year.
Update: I changed the model so that the PRC timeline is dependent on the US timeline. The values didn't change perceptibly, updated text here (might crosspost eventually).
I didn't include a US non-race timeline because I was assuming that "we" is the US and can mainly only causally influence what the US does. (This is not strictly true, but I think it's true enough).
I read the MAGIC paper, and my impression is that it would be an international project, in which the US might play a large role. But my impression is also that MAGIC would be very willing to cause large delays in the development of TAI in order to ensure safety, which is why I added 20 years to the timeline. I think that a non-racing US would be still much faster than that, because they are less concerned with safety/less bureaucratic/willing to externalize costs on the world.
Also, the US race and PRC race shouldn't be independent distributions. A still inaccurate but better model would be to use the same distribution for USA and then have PRC be e.g. 1 year behind +/- some normally distributed noise with mean 0 and SD 1 year.
Hm. That does sound like a much better way of modeling the situation, thanks! I'll put it on my TODO list to change this. That would at least decrease variance, right?
I like this kind of take!
I disagree with many of the variables, and have a bunch of structural issues with the model (but like, I think that's always the case with very simplified models like this). I think the biggest thing that is fully missing is the obvious game-theoretic consideration. In as much as both the US and China think the world is better off if we take AI slow, then you are in a standard prisoners dilemma situation with regards to racing towards AGI.
Doing a naive CDT-ish expected-utility calculation as you do here will reliably get people the wrong answer in mirrored prisoner's dilemmas, and as such you need to do something else here.
Doing a naive CDT-ish expected-utility calculation
I'm confused by this. Someone can endorse CDT and still recognize that in a situation where agents make decisions over time in response to each other's decisions (or announcements of their strategies), unconditional defection can be bad. If you're instead proposing that we should model this as a one-shot Prisoner's Dilemma, then (1) that seems implausible, and (2) the assumption that US and China are anything close to decision-theoretic copies of each other (such that non-CDT views would recommend cooperation) also seems implausible.
I guess you might insist that "naive" and "-ish" are the operative terms, but I think this is still unnecessarily propagating a misleading meme of "CDT iff defect."
Someone can endorse CDT and still recognize that in a situation where agents make decisions over time in response to each other's decisions (or announcements of their strategies), unconditional defection can be bad. If you're instead proposing that we should model this as a one-shot Prisoner's Dilemma
Well, to be more formal and specific, under CDT, the multi-shot Prisoner's Dilemma still unravels from the back into defect-defect at every stage as long as certain assumptions are satisfied, such as the number of stages being finite or there being no epsilon-time discounting.[1]
Even when you deal with a potentially infinite-stage game and time-discounting, the Folk theorems make everything very complex because they tend to allow for a very wide variety of Nash equilibria (which means that coordinating on those NEs becomes difficult, such as in the battle of the sexes), and the ability to ensure the stability of a more cooperative strategy often depends on the value of the time-discounting factor and in any case requires credibly signaling that you will punish defectors through grim trigger strategies that often commit you long-term to an entirely adversarial relationship (which is quite risky to do in real life, given uncertainties and the potential need to change strategies in response to changed circumstances).
The upshot is that the game theory of these interactions is made very complicated and multi-faceted (in part due to the uncertainty all the actors face), which makes the "greedy" defect-defect profile much more likely to be the equilibrium that gets chosen.
- ^
"defecting is the dominant strategy in the stage-game and, by backward induction, always-defect is the unique subgame-perfect equilibrium strategy of the finitely repeated game."
Sure, you can think about this stuff in a CDT framework (especially over iterated games), though it is really quite hard. Remember, the default outcome in a n-round prisoners dilemma in CDT is still constant defect, because you just argue inductively that you will definitely be defected on in the last round. So it being single shot isn't necessary.
Of course, the whole problem with TDT-ish arguments is that we have very little principled foundation of how to reason when two actors are quite imperfect decision-theoretic copies of each other (like the U.S. and China almost definitely are). This makes technical analysis of the domains where the effects from this kind of stuff is large quite difficult.
Remember, the default outcome in a n-round prisoners dilemma in CDT is still constant defect, because you just argue inductively that you will definitely be defected on in the last round. So it being single shot isn't necessary.
I think the inductive argument just isn't that strong, when dealing with real agents. If, for whatever reason, you believe that your counterpart will respond in a tit-for-tat manner even in a finite-round PD, even if that's not a Nash equilibrium strategy, your best response is not necessarily to defect. So CDT in a vacuum doesn't prescribe always-defect, you need assumptions about the players' beliefs, and I think the assumption of Nash equilibrium or common knowledge of backward induction + iterated deletion of dominated strategies is questionable.
Also, of course, CDT agents can use conditional commitment + coordination devices.
the whole problem with TDT-ish arguments is that we have very little principled foundation of how to reason when two actors are quite imperfect decision-theoretic copies of each other
Agreed!
I think you can get cooperation on an iterated prisoners dilemma if there's some probability p that you play another round, if p is high enough - you just can't know at the outset exactly how many rounds there are going to be.
Yep, it's definitely possible to get cooperation in a pure CDT-frame, but it IMO is also clearly silly how sensitive the cooperative equilibrium is to things like this (and also doesn't track how I think basically any real-world decision-making happens).
I do think that iterated with some unknown number of iterations is better than either single round or n-rounds at approximating what real world situations look like (and gets the more realistic result that cooperation is possible).
I agree that people are mostly not writing out things out this way when they're making real world decisions, but that applies equally to CDT and TDT, and being sensitive to small things like this seems like a fully general critique of game theory.
To be clear, uncertainty about the number of iterations isn’t enough. You need to have positive probability on arbitrarily high numbers of iterations, and never have it be the case that the probability of p(>n rounds) is so much less than p(n rounds) that it’s worth defecting on round n regardless of the effect of your reputation. These are pretty strong assumptions.
So cooperation is crucially dependent on your belief that all the way from 10 rounds to Graham’s number of rounds (and beyond), the probability of >n rounds conditional on n rounds is never lower than e.g. 20% (or whatever number is implied by the pay-off structure of your game).
Huh, I do think the "correct" game theory is not sensitive in these respects (indeed, all LDTs cooperate in a 1-shot mirrored prisoner's dilemma). I agree that of course you want to be sensitive to some things, but the kind of sensitivity here seems silly.
I think the biggest thing that is fully missing is the obvious game-theoretic consideration. In as much as both the US and China think the world is better off if we take AI slow, then you are in a standard prisoners dilemma situation with regards to racing towards AGI.
Yep, that makes sense. When I went into this, I was actually expecting the model to say that not racing is still better, and then surprised by the outputs of the model.
I don't know how to quantitatively model game-theoretic considerations here, so I didn't include them, to my regret.
As an advocate for an international project, I am not advocating for individual actors to self-sacraficially pause while their opponent continues. Even if it were the right thing to do, it seems politically non-viable, and it isn't remotely necessary as a step towards building a treaty, it may actually make us less likely to succeed by seeming to present our adversaries with an opportunity to catch up and emboldening them to compete.
Slight variation: If China knew that you weren't willing to punish competition with competition, that eliminates their incentive to work toward cooperation!
Then my analysis was indeed not directed at you. I think there are people who are in favor of unilaterally pausing/ceasing, often with specific other policy ideas.
And I think it's plausible that ex ante/with slightly different numbers, it could actually be good to unilaterally pause/cease, and in that case I'd like to know.
Well let's fix this then?
I find that it is better than not racing. Advocating for an international project to build TAI instead of racing turns out to be good if the probability of such advocacy succeeding is ≥20%.
Both of these sentences are false if you accept that my position is an option (racing is in fact worse than international cooperation which is encompassed within the 'not racing' outcomes, and advocating for an international project is in fact not in tension with racing whenever some major party is declining to sign on.)
There are actually a lot of people out there who don't think they're allowed to advocate for a collective action without cargo culting it if the motion fails, so this isn't a straw-reading.
Hm, interesting. This suggests an alternative model where the US tries to negotiate, and there are four possible outcomes:
- US believes it can coordinate with PRC, creates MAGIC, PRC secretly defects.
- US believes it can coordinate with PRC, creates MAGIC, US secretly defects.
- US believes it can coordinate with PRC, both create MAGIC, none defect.
- US believes it can't coordinate with PRC, both race.
One problem I see with encoding this in a model is that game theory is very brittle, as correlated equilibria (which we can use here in place of Nash equilibria, both because they're easier to compute and because the actions of both players are correlated with the difficulty of alignment) can change drastically with small changes in the payoffs.
I hadn't informed myself super thoroughly about the different positions people take on pausing AI and the relation to racing with the PRC, my impression was that people were not being very explicit about what should be done there, and the people who were explicit were largely saying that a unilateral ceasing of TAI development would be better. But I'm willing to have my mind changed on that, and have updated based on your reply.
Defecting becomes unlikely if everyone can track the compute supply chain and if compute is generally supposed to be handled exclusively by the shared project.
I am not as convinced as many other people of compute governance being sufficient, both because I suspect there are much better architectures/algorithms/paradigms waiting to be discovered, which could require very different types of (or just less) compute (which defectors could then use), and all from what I've read so far about federated learning has strengthened my belief that part of the training of advanced AI systems could be done in federation (e.g. search). If federated learning becomes more important, then the existing stock of compute countries have also becomes more important.
It seems important to establish whether we are in fact going to be in a race and whether one side isn't already far ahead.
With racing, there's a difference between optimizing the chance of winning vs optimizing the extent to which you beat the other party when you do win. If it's true that China is currently pretty far behind, and if TAI timelines are fairly short so that a lead now is pretty significant, then the best version of "racing" shouldn't be "get to the finish line as fast as possible." Instead, it should be "use your lead to your advantage." So, the lead time should be used to reduce risks.
Not sure this is relevant to your post in particular; I could've made this point also in other discussions about racing. Of course, if a lead is small or non-existent, the considerations will be different.
Yep, makes sense. I think if I modify the model to shorten timelines & widen the gap between PRC and US the answer could flip.
Strong agree on the desire for conversations to go more like this, with models and clearly stated variables and assumptions. Strong disagree on the model itself, as I think it's missing some critical pieces. I feel motivated now to make my own model which can show the differences that stem from my different underlying assumptions.
If this makes you create your own model to argue against mine, then I've achieved my purpose and I'm happy
:-D
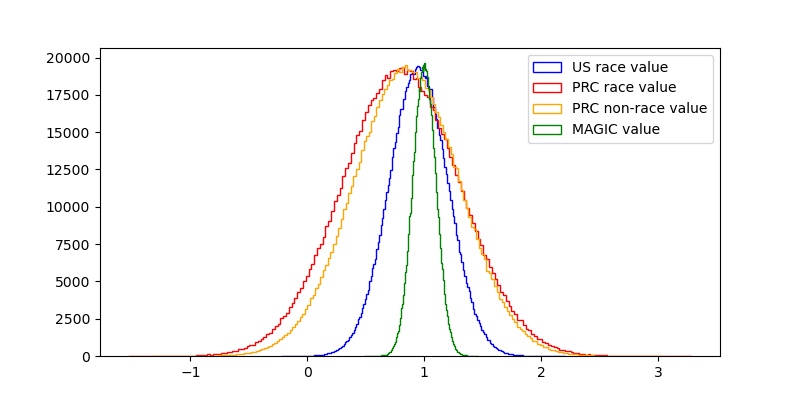
I that in the mean & median cases, value(MAGIC)>value(US first, no race)>value(US first, race)>value(PRC first, no race)>value(PRC first, race)>value(PRC first, race)≫value(extinction)
While I think the core claim "across a wide family of possible futures, racing can be net beneficial" is true, the sheer number of parameters you have chosen arbitrarily or said "eh, let's assume this is normally distributed" demonstrates the futility of approaching this question numerically.
I'm not sure there's added value in an overly complex model (v.s. simply stating your preference ordering). Feels like false precision.
Presumably hardcore Doomers have:
value(SHUT IT ALL DOWN) > 0.2 > value(MAGIC) > 0 = value(US first, no race)=value(US first, race)=value(PRC first, no race)=value(PRC first, race)=value(PRC first, race)=value(extinction)
Whereas e/acc has an ordering more like:
value(US first, race)>value(PRC first, race)>value(US first, no race)>value(PRC first, no race)>value(PRC first, race)>value(extinction)>value(MAGIC)
There's two arguments you've made, one is very gnarly, the other is wrong :-):
- "the sheer number of parameters you have chosen arbitrarily or said "eh, let's assume this is normally distributed" demonstrates the futility of approaching this question numerically."
- "simply stating your preference ordering"
I didn't just state a preference ordering over futures, I also ass-numbered their probabilities and ass-guessed ways of getting there. For to estimate an expected value of an action, one requires two things: A list of probabilities, and a list of utilities—you merely propose giving one of those.
(As for the "false precision", I feel like the debate has run its course; I consider Scott Alexander, 2017 to be the best rejoinder here. The world is likely not structured in a way that makes trying harder to estimate be less accurate in expectation (which I'd dub the Taoist assumption, thinking & estimating more should narrow the credences over time. Same reason why I've defended the bioanchors report against accusations of uselessness with having distributions over 14 orders of magnitude).
value(SHUT IT ALL DOWN) > 0.2 > value(MAGIC) > 0 = value(US first, no race)=value(US first, race)=value(PRC first, no race)=value(PRC first, race)=value(PRC first, race)=value(extinction)
Yes, that is essentially my preference ordering / assignments, which remains the case even if the 0.2 is replaced with 0.05 -- in case anyone is wondering whether there are real human beings outside MIRI who are that pessimistic about the AI project.
A common scheme for a conversation about pausing the development of transformative AI goes like this:
Minor: The first linked post is not about pausing AI development. It mentions various interventions for "buying time" (like evals and outreach) but it's not about an AI pause. (When I hear the phrase "pausing AI development" I think more about the FLI version of this which is like "let's all pause for X months" and less about things like "let's have labs do evals so that they can choose to pause if they see clear evidence of risk".)
At a basic level, we want to estimate how much worse (or, perhaps, better) it would be for the United States to completely cede the race for TAI to the PRC.
My impression is that (most? many?) pause advocates are not talking about completely ceding the race to the PRC. I would guess that if you asked (most? many?) people who describe themselves as "pro-pause", they would say things like "I want to pause to give governments time to catch up and figure out what regulations are needed" or "I want to pause to see if we can develop AGI in a more secure way, such as (but not limited to) something like MAGIC."
I doubt many of them would say "I would be in favor of a pause if it meant that the US stopped doing AI development and we completely ceded the race to China." I would suspect many of them might say something like "I would be in favor of a pause in which the US sees if China is down to cooperate, but if China is not down to cooperate, then I would be in favor of the US lifting the pause."
I doubt many of them would say "I would be in favor of a pause if it meant that the US stopped doing AI development and we completely ceded the race to China." I would suspect many of them might say something like "I would be in favor of a pause in which the US sees if China is down to cooperate, but if China is not down to cooperate, then I would be in favor of the US lifting the pause."
FWIW, I don't think this super tracks my model here. My model is "Ideally, if China is not down to cooperate, the U.S. threatens conventional escalation in order to get China to slow down as well, while being very transparent about not planning to develop AGI itself".
Political feasibility of this does seem low, but it seems valuable and important to be clear about what a relatively ideal policy would be, and honestly, I don't think it's an implausible outcome (I think AGI is terrifying and as that becomes more obvious it seems totally plausible for the U.S. to threaten escalation towards China if they are developing vastly superior weapons of mass destruction while staying away from the technology themselves).
I think the PRC is behind on TAI, compared to the US, but only about one year.
Unless TAI is close to current scale, there will be an additional issue with hardware in the future that's not yet relevant today. It's not insurmountable, but it costs more years.
This is a good concept. I built a similar Squiggle model a few weeks ago* (although it's still a rough draft), I hadn't realized you'd beaten me to it. So I guess you won the race to build an arms race model? :P
If I'm reading this right, it looks like the model assumes that if the US doesn't race, then China gets TAI first with 100% probability. That seems wrong to me. Race dynamics mean that when you go faster, the other party also goes faster. If the US slows down, there's a good chance China also slows down.
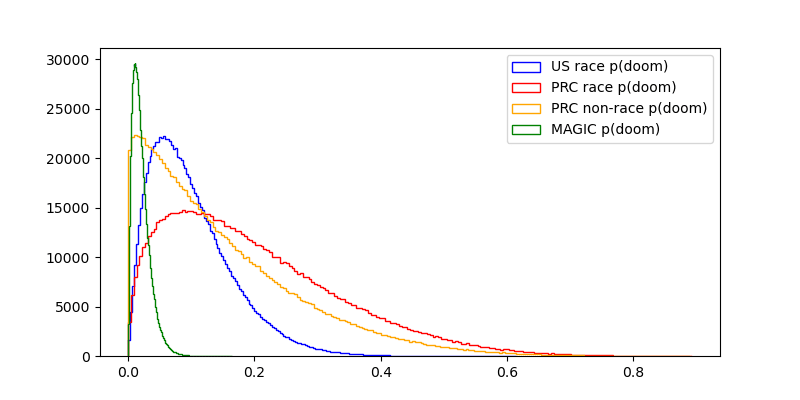
Also, regarding specific values, the model's average P(doom) values are:
- 10% if race + US wins
- 20% if race + China wins
- 15% if no race + China wins
That doesn't sound right to me. Racing is very bad for safety and right now the US leaders are not going a good job, so I think P(doom | no race & China wins) is less than P(doom | race & US wins). Although I think this is pretty debatable.
*My model found that racing was bad and I had to really contort the parameter values to reverse that result. I haven't thought much about the model construction so there could be unfair built-in assumptions.
This is a good concept. I built a similar Squiggle model a few weeks ago* (although it's still a rough draft), I hadn't realized you'd beaten me to it. So I guess you won the race to build an arms race model? :P
Good thing building these kinds of models doesn't kill everyone ;-)
If I'm reading this right, it looks like the model assumes that if the US doesn't race, then China gets TAI first with 100% probability. That seems wrong to me. Race dynamics mean that when you go faster, the other party also goes faster. If the US slows down, there's a good chance China also slows down.
Hm, that's a good point. I don't know how to express that cleanly, but there are other intermediate options in which the US moves slower, but still enough that there's a >50% chance of them getting TAI first, or they pull the brakes & alarms so that the PRC also slows down. I don't know how to model this, maybe I would if I knew differential equations better?
Also, regarding specific values, the model's average P(doom) values are: […] That doesn't sound right to me.
For transparency, my current personal p(doom)≈60% (mostly race scenarios), and p(doom|no race)≈45%. My guess is that transparent CoTs, mild optimization, trying to automate mechinterp, control schemes &c "eat" some of the probability of extinction, but then you're stuck in worlds where doing obvious things doesn't actually help you align superintelligences and the problem is genuinely hard. So racing is pretty bad for safety. (I used different values in this post because I wanted to take the perspective of the median reader).
I saw your model on squigglehub, but didn't dig into it too deeply. I encourage you to post it on here with or without an explanation :-)
Hm, that's a good point. I don't know how to express that cleanly, but there are other intermediate options in which the US moves slower, but still enough that there's a >50% chance of them getting TAI first, or they pull the brakes & alarms so that the PRC also slows down.
You could model it as a binary P(US wins | US races) and P(US wins | US does not race). A continuum would be more accurate but I think a binary is basically fine.
I saw your model on squigglehub, but didn't dig into it too deeply. I encourage you to post it on here with or without an explanation :-)
Posting the model is on my to-do list but I am not very satisfied with it right now so I want to fix it up some more. I want to make a bigger model that looks at all the main effects of slowing down, not just race dynamics, although perhaps that's too ambitious.
norvid_studies: "If Carthage had won the Punic wars, would you notice walking around Europe today?"
Will PRC-descended jupiter brains be so different from US-descended ones?
I suppose this will depend a lot on the AI alignment and how much the AI takes control of the world.
If Carthage had won the war and then built a superhuman AI aligned to their values, we probably would notice.