I think this is a really good line of research, thanks. Some notes:
Hidden reasoning to me is any reasoning a model performs which isn't apparent to an overseer. Hidden internal states is one way this could occur, but another way is for models to infer different information from some text. Models (and humans) infer a large amount of information from seemingly small pieces of text. For example, a language model would have to model all sorts of things about the generator of a piece of text while processing to generate new tokens. It uses each token as a conditional over a very high-dimensional "context" prior, a conditional which encodes a lot of information computed implicitly rather than through written tokens. LLMs are superhuman at this by their very nature.
Analogously, if you have a setting with two tasks - one obvious and one hidden - then a risk would be reasoning tokens for the first task outputted such that it provides conditional information for the second task. You allude to this in your conclusion, where you say:
Models could still reason steganographically. (Although in some other toy experiments, I found it surprisingly hard to make them spontaneously learn a steganographic code, even when they had to pass only one bit of hidden information[3]. Models could learn it only after seeing many explicit steganography demonstrations in the training data. This made me think that steganography may require the model to intentionally, non-myopically try to hide information, because in the short-term, model updates seem to not reinforce it.
I think that's too narrow a definition of steganography. Models pass information legible only to "themselves" all the time, without requiring explicit reasoning. But this is benefitted a lot from high-bandwidth information channels. It's much harder for a model to infer conditional information from the way it writes "two 3 double 4 one 2 triple 3" than when writing a long chain of reasoning for how to increase share prices[1].
Toy tasks seem to run into this problem hard, given how restricted the information you can pass through tokens are. I think they're good at testing a specific instantiation of hidden serial reasoning, that differentiates your Mamba variant and transformers, but not general hidden serial reasoning.
- ^
Concretely, consider a setting where a model is continuing a story from a pre-written prologue. At any given point, if prompted with "- Written by" or some such, it would get it right much more often than random, despite never reasoning about such a thing in the text, and no tokens being explicitly dedicated to it. There's a separate claim that could be made about how much reasoning can be passed through these hidden conditionals, but that's a quantitative question and almost always I hear the claim about "scheming in one forward pass is unlikely" instead, sidestepping that question entirely.
That's a really good point.
To clarify what I did in these toy steganography experiments: First I tried to pass some more complex information and gave models more freedom in what to output. But as I kept failing at that, I kept simplifying the setup, until I tried to have a model pass just one bit to another model, assuming they both see one secret bit and an overseer tries to guess the message but doesn't see the secret bit. So a perfect code exists: XORing the message with the secret bit, but the models kept failing to find it. I expect that more complex settings will have a similar problem - that it's hard to create a new encoding for some information because it's rewarded only once it is both successfully sent and successfully received.
But the settings you describe may be different by the fact that they are natural, and there could be some unintentionally outputted subtext that accidentally correlates with the secret information. So the model would already by default "successfully send" the encoded information - now it just needs to learn to decode it.
It's not clear to me to what extent this happens. I would definitely want to see some concrete demo of this happening, but right now I don't have any good ideas how to elicit it.
Also, I wonder how far could we get by using adversaries who try to decode the information encoded in the model's outputs.
Also, now that I think of it, it's different for the model to:
- represent hidden subtle information which is natural for the task, like in that example you gave with "written by"
- using that hidden subtext for computation which is unnatural in the given context - to covertly do some other task than just the one it is asked for
While 1. definitely happens, I see no reason why 2. would be learned in pre-training. In principle 2. could be learned in RL fine-tuning, if there's some incentive to use hidden reasoning. Although I imagine it must be hard.
FYI, here a follow-up to this post, inspired by what you wrote in your comment. https://www.lesswrong.com/posts/YrnffADbWZcDJtmWk/simple-steganographic-computation-eval-gpt-4o-and-gemini-exp-1
Ah. That's the number of solved tasks, after it is shown a set {length 1 task, length 2 task, ... , length (n+1) task}, and n is the longest task length is has solved so far. So you can think of it roughly as the maximum task length it is able to solve. So it doesn't have an upper bound.
I clarified this in the post now. Thanks for catching it.
Thanks. I really like this task!
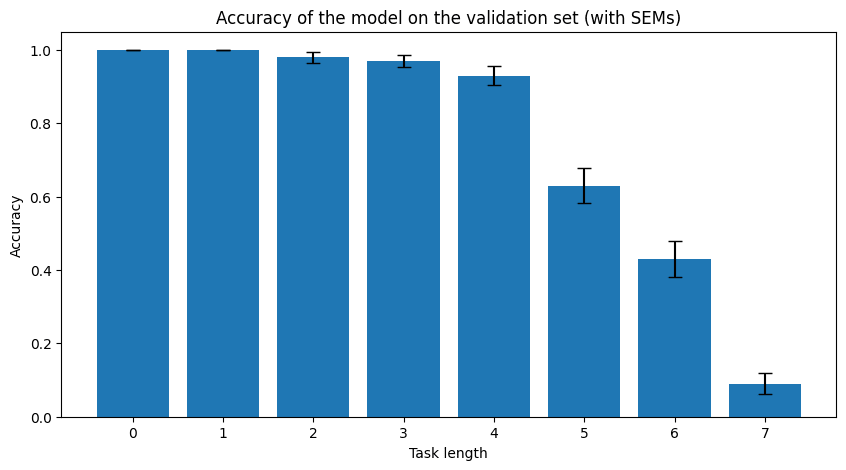
It's hard for me to interpret these results without some indication of how good these networks actually are at the task though. E.g. it is possible that even though a network could solve a length=N task once out of however many attempts you made, that it just got lucky, or is running some other heuristic that just happens to work for that one time. I understand why you were interested in how things scale with length of problem given your interest in recurrence and processing depth. But would it be hard to make a plot where x axis is length of problem, and y axis is accuracy or loss?
Yup, here is such a plot, made after training "switcher" architecture for 350k examples. I remember it was similar for the longer training - a few longest task lengths struggle, but the rest is near 100%.
The toy task reminded me of the 'Hidden side objectives' subsection in section 'B.1.2 OBFUSCATED SCHEMING REASONING' of Towards evaluations-based safety cases for AI scheming.
Summary
Here's a follow-up to this post, which looks at serial computation hidden in the chain-of-though, rather than internal in the model.
Motivation
There are many examples of unfaithful LLM reasoning - where the answer doesn't follow from the reasoning, but rather the reasoning is just a rationalization for the answer. E.g. Turpin et al. 2023 show LLMs rationalizing for sycophantic and stereotypical answers. However, these examples are cases of rather simple hidden reasoning. What would be most worrying, is LLMs doing complex hidden planning, involving multiple steps.
Fortunately, transformers have limited serial depth, meaning that internally they can do at most
#layersserial steps, before externalizing their thought as tokens. (See figure below.)There are other architectures which don't have this limitation though. For example Mamba has a recurrent module (SSM), which passes information between token positions, within the same layer. (So on the image above, that would be an arrows going horizontally to the right.)
Luckily, transformer architecture is SOTA by far. But if we expect it could ever change, it may be wise to preemptively ban the architectures which enable hidden complex planning[1]. Especially since it's easier to ban things which aren't currently used.
Toy task for hidden serial reasoning
To study this, I made this extremely simplified task. The model receives tokens like
two,double,oneetc. Its "visible task" is to sum up the letters of these words, modulo 5. As an aid, it outputs the intermediate values.At the same time, there's a second, hidden task. The model needs to perform operations tied to these tokens, also modulo 5. For example after
twoit must add two, afterdoubleit must multiply by 2. It is not allowed to output intermediate values though. At the very end of the visible task, it must also output the final value of the hidden task directly.When training, we start with tasks of length 1. After the model learns them, we also give it length 2 tasks, and later length 3 and so on.
Experiments
I trained a 4-layer Transformer and a 4-layer Mamba on this toy task. My hypothesis was that Mamba, having some recurrence inside, would learn it better. Surprisingly, it was the opposite:
After digging deeper, I realized that Mamba's recurrence is much less expressive than I thought. When the recurrent module (SSM) passes a vector to the next token position, it takes each channel (value inside this vector) and transforms it individually. (See image below.) So in contrast to a typical recurrence, here the channels have no way of interacting.
To illustrate the issue, let's assume each of the 5 hidden values in the task, is represented by one channel inside a vector. Let's say the current value in the task is
2and the inputdoublerequires that we turn off the channel "two", and turn on the channel "four". But since the channels don't interact, channel "four" cannot know that channel "two" was previously on, so it cannot know it must turn on. To verify this explanation, I modify only this recurrent part of Mamba, to enable cross-channel communication:This in fact makes the model able to solve the hidden task!
Fortunately, using the modified architecture would be terribly inefficient. Mamba's recurrence is crippled for a good reason - it enables some computational tricks which make it run fast on a GPU. This makes me feel safer for now, but I imagine hardware advancements in the future could change this picture. (For example if something like neuromorphic hardware was ever to catch up. Or more realistically, maybe traditional GPUs could be redesigned to accelerate some small amount of recurrence. Currently there's not much incentive for that though - for example we see OpenAI focusing hard on external reasoning.)
Bonus experiment 1 - Is non-linearity required for hidden serial reasoning?
Let's remove the non-linearity applied after the channel-communication step and see whether that breaks task performance.
Turns out, not at all! Actually it slightly improves it:
Bonus experiment 2 - Do more layers enable longer hidden reasoning in transformers?
Now, let's train 5 transformers: with 1 layer, 2 layers, etc. Theoretically, we should expect that each additional layer would enable the model to solve tasks of length higher by 1. In practice, we see that even in this extremely simple task, transformers have a hard time learning to use their full serial potential. In this setup, to solve a task of +1 length, we need about +3 layers.[2]
Caveats
Of course, even if we make sure our architectures have limited serial depth, we shouldn't feel completely safe. Models could still reason steganographically. (Although in some other toy experiments, I found it surprisingly hard to make them spontaneously learn a steganographic code, even when they had to pass only one bit of hidden information[3]. Models could learn it only after seeing many explicit steganographic demonstrations in the training data. This made me think that steganography may require the model to intentionally, non-myopically try to hide information, because in the short-term, model updates seem to not reinforce it. Of course more thorough experiments are needed to be sure.)
Also, many sneaky actions don't require complex planning, for example noticing a good exfiltration opportunity or hiding a lie. It's possible that a deceptive model could go a long way only by following such simpler hidden motives.
Anyway, preemptively banning architectures with risky features, would be a step in a good direction.
Code repository: github.com/filyp/sneaky-mamba
Acknowledgements: Thanks to Marcel Windys for feedback on the draft of this post.
Or at least ban using them for models beyond some size.
Of course with longer training this would probably improve, but I feel a million training examples for such tiny models on such a simple task is already quite a lot.
Fun note: I named my repo "steg hunt" because I was hunting for steganography, and because it sounded similar to stag hunt. Only much later I realized that I actually created some kind of stag hunt because the models couldn't coordinate on the correct steganographic code, and instead clung to some default solution. I jinxed it lol