This is a very basic question to ask, but I'm not sure I actually understand some fundamental properties people seem to ascribe to correlation.
As far as I understand it, correlation usually refers to Pearson's correlation coefficient, which is, according to Wikipedia, "a correlation coefficient that measures linear correlation between two sets of data." Cool.
But then I see a discussion on whether variables X and Y are related in some way, and reads like:
- well, X correlates to Y with r=0.8 so it's a good predictor/proxy/whatever
- X and Y have been found to correlate with r = 0.05, so its not a good predictor/proxy/whatever
For the first one, I'm OK. For the second one, not so much:
looking at Anscombe's Quartet:
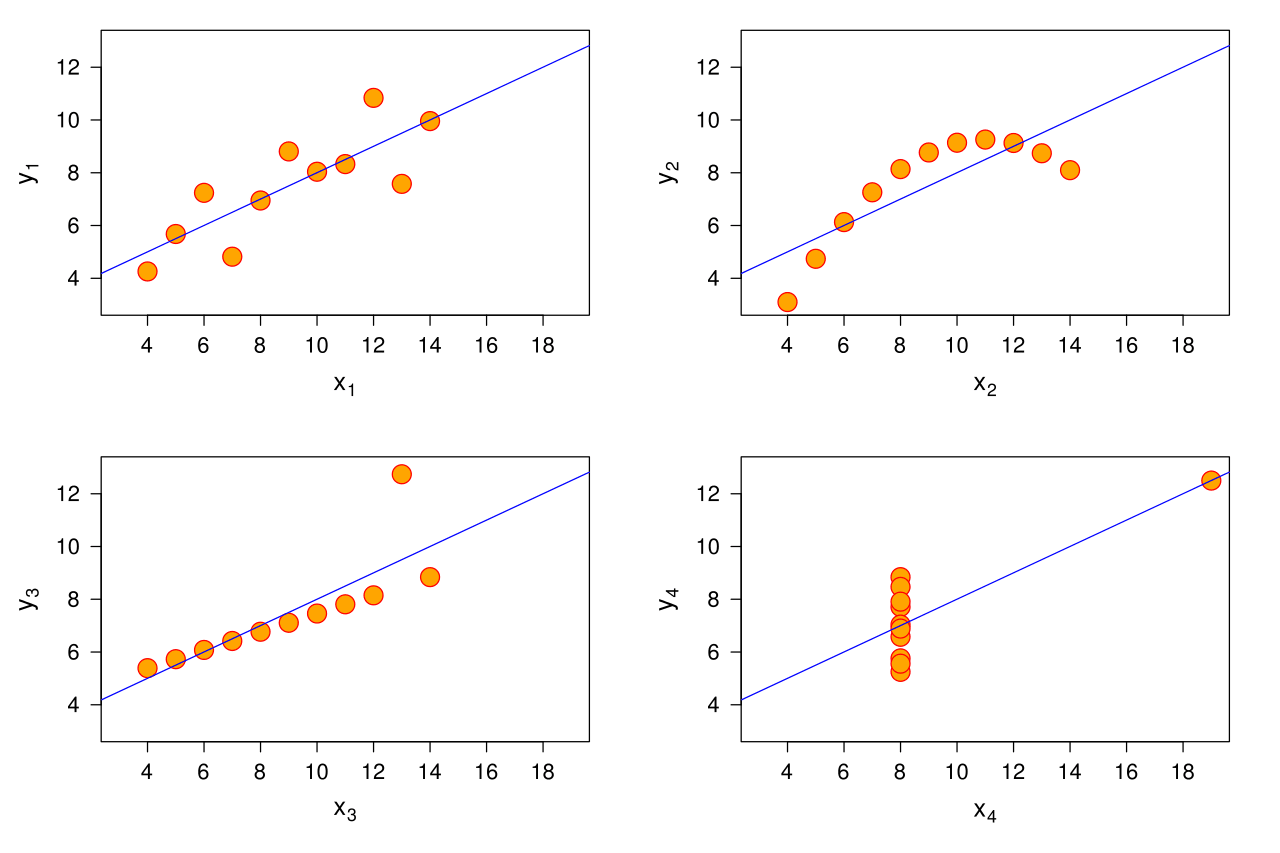
It would seem that even though correlation (and therefore R²) are the same for all 4 datasets, the upper-rightmost one could be an Y completely dependent on X, probably a polynomial of some kind (in which case, Y could be perfectly explained by X), whereas in the down-rightmost one Y couldn't be explained as a function of X, of any kind.
Now, I understand that correlation only measures how linearly two variables are related, but again, in the same example, it would seem that we would be better served by considering other, non-linear ways they could be related.
Since correlation is such an extended way of measuring the relationships of X and Y, across many levels of competence and certainly among people I know understand this much better than I do, my questions are:
Why is, besides being the most nice/common/useful type of relation, linear relationship privileged in the way I described above? Why is it OK to say that X is not a good predictor of Y because r=0.05, which I'm understanding as "It has a bad linear relation", without adressing other ways they could be related, such as a grade 27 polynimial? Is the fact that they are "badly" linearly related enough to explain that they won't be related any other way?
Again, this a very basic lagoon I've just recently found on myself, so an explanation on any level would be very appreciated
Spearman (rank) correlation is often a good alternative for nonlinear relationships.
That's not quite right. It measures the strength of monotonic relationships, which which may also be linear. So this measure is more general than Pearson correlation. It just measures whether, if one value increases, the other value increases as well, not whether they increase at the same rate.