Thanks for sharing this, I believe this kind of work is very promising. Especially, it pushes us to be concrete.
I think some of the characteristics you note are necessary side effects of fast parallel computation. Take this canonical constant-depth adder from pg 6 of "Introduction to Circuit Complexity":
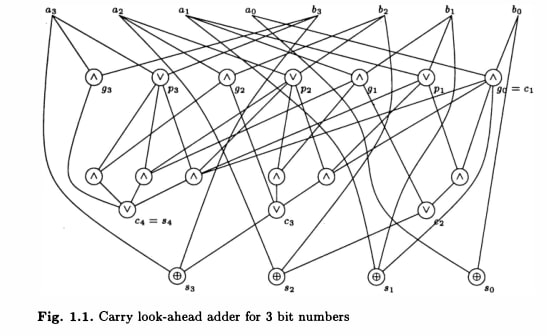
Imagine the same circuit embedded in a neural network. Individual neurons are "merely" simple Boolean operations on the input - no algorithm in sight! More complicated problems often have even messier circuits, with redundant computation or false branches that must be suppressed.
Or imagine a typical program for checking legal moves, some nested for loops. If you actually compile and run such a program you will see the processor perform a long series of local checks. Without the source code any "algorithmness" that remains is in the order those checks are performed in. Now imagine porting that same program to a parallel architecture, like a transformer or the brain. With the checks occurring in parallel there's no obvious systematicity and the whole thing could be mistaken for a mass of unrelated local computations, the algorithm totally obscured. Even more so if the medium is stochastic.
Actually this relates to a problem in circuit complexity - the notion of algorithm itself becomes more subtle. Since circuits are of fixed finite size, they can only accept one size of input. So, in order to solve a task at any size (as Turing machines do) a different circuit is required for each n. But then what's to keep each circuit in the family from being wildly different? How could such an infinitely varied family represent a crisp, succinct algorithm? Besides, this arbitrariness lends a sort of unchecked power, for instance the ability to solve the halting problem! (e.g. by hard coding every answer for each n). To tame this, the notion of "uniform complexity" is introduced. A series of circuits is uniform iff the circuits themselves can be generated by a Turing machine. So an "algorithm" is a finite description of a fast parallel circuit for every size.
This seems like it may apply directly for the case of OthelloGPT. If the list of "heuristics" permit a short generating description, they may indeed represent a crisp algorithm - only implemented in parallel. It would be v. interesting if gradient descent preferred such solutions since the generating rule is only ever implicit. If gradient descent had such a preference it could substitute directly for a more traditional notion of algorithm in many arguments (e.g. about generalization/reasoning/world modeling). Really, any idea of which sort of circuits gradient descent prefers in this case could help illuminate how "deep learning works" at all.
Interesting stuff!
Perhaps a smaller model would be forced to learn features in superposition -- or even nontrivial algorithms -- in a way more representative of a typical LLM.
I'm unsure whether or not it's possible at all to express a "more algorithmic" solution to the problem in a transformer of OthelloGPT's approximate size/shape (much less a smaller transformer). I asked myself "what kinds of systematic/algorithmic calculations could I 'program into' OthelloGPT if I were writing the weights myself?", and I wasn't able to come up with much, though I didn't think very hard about it.
Curious if you have thoughts on this?
Roughly, this is hard because, for any given internal representation that a transformer computes, it can't access that representation at earlier positions when computing the same representation at later ones (cf). For example, if there's some layer at which the board state is basically "finalized," OthelloGPT can't use these finalized representations of past states to compute the current state. (By the time it is able to look back at past finalized states, it's too late, the current state is already finalized.)
So, when we use info about the past to compute the current board state, this info can't just be the board state, it has to be "only partway computed" in some sense. This rules out some things that feel intuitive and "algorithmic," like having a modular component that is fully (and only) responsible for deciding which pieces get flipped by a given move. (In order to know which pieces get flipped now, you need to know which pieces are mine/yours, and that depends on which ones got flipped in the past. So a "flip calculator" would need to use its own past outputs as current inputs, and transformers can't be recurrent like this.)
It looks like for OthelloGPT, the relevant sense of "only partway computed" is "probably true based on heuristics, but not necessarily true." I guess one can imagine other ways of organizing this computation inside a transformer, like computing the state of the upper half of the board first, then the lower half (or upper left corner first, or whatever). That seems like a bad idea, since it will leave capacity unused when the game is confined only to a proper subset of these regions. Maybe there are other alternatives I haven't thought of? In any case, it's not obvious to me that there's a feasible "more algorithmic" approach here.
I am also unsure how feasible it is to solve the problem using rules that generalize across positions. More precisely, I'm not sure if such an approach would really be simpler than what OthelloGPT does.
In either case, it has to (in some sense) iterate over all positions and check separately whether each one is legal. In practice it does this with distinct neurons/circuits that are mapped to distinct absolute positions -- but if it instead used a computation like "check for a certain pattern in relative position space," it would still need to repeat this same check many times over within the same forward pass, to handle all the copies of that pattern that might appear at various places on the board. And it's not obvious that repeating (some number of distinct rules) x (some other number of potential applications per rule) is cheaper than just repeating the full conditions that license a move once for each absolute position on the board.
I think it's pretty plausible that this is true, and that OthelloGPT is already doing something that's somewhat close to optimal within the constraints of its architecture. I have also spent time thinking about the optimal algorithm for next move prediction within the constraints of the OthelloGPT architecture, and "a bag of heuristics that promote / suppress information with attention to aggregate information across moves" seems like a very reasonable approach.
Seems like the natural next step would be to try to investigate grokking, as this appears analogous: you have a model which has memorized or learned a grabbag of heuristics & regularities, but as far as you can tell, the algorithmic core is eluding the model despite what seems like ample parameterization & data, perhaps because it is a wide shallow model. So one could try to train a skinny net, and maybe aggressively subsample the training data down into a maximally diverse subset. If it groks, then one should be able to read off much more interpretable algorithmic sub-models.
Very strongly agree with the size considerations for future work, but would be most interested to see if a notably larger size saw less "bag of heuristics" behavior and more holistic integrated and interdependent heuristic behaviors. Even if the task/data at hand is simple and narrowly scoped, it may be that there are fundamental size thresholds for network organization and complexity for any given task.
Also, I suspect parameter to parameter the model would perform better if trained using ternary weights like BitNet 1.5b. The scaling performance gains at similar parameter sizes in pretraining in that work makes sense if the ternary constraint is forcing network reorganization instead of fp compromises in cases where nodes are multi-role. Board games, given the fairly unambiguous nature of the data, seems like a case where this constrained reorganization vs node compromises would be an even more significant gain.
It might additionally be interesting to add synthetic data into the mix that was generated from a model trained to predict games backwards. The original Othello-GPT training data had a considerable amount of the training data as synthetic. There may be patterns overrepresented in forward generated games that could be balanced out by backwards generated gameplay. I'd mostly been thinking about this in terms of Chess-GPT and the idea of improving competency ratings, but it may be that expanding the training data with bi-directionally generated games instead of just unidirectional generated synthetic games reduces the margin of error in predicting non-legal moves further with no changes to the network training itself.
Really glad this toy model is continuing to get such exciting and interesting deeper analyses.
Do you think a vision transformer trained on 2-dimensional images of the board state would also come up with a bag of heuristics or would it naturally learn a translation invariant algorithm taking advantage of the uniform way the architecture could process the board? (Let's say that there are 64 1 pixel by 1 pixel patches, perfectly aligned with the 64 board locations of an 8x8 pixel image, to make it maximally "easy" for both the model and for interpretability work.)
And would it differ based on whether one used an explicit 2D positional embedding, or a learned embedding, or a 1D positional embedding that ordered the patches from top to bottom, right to left?
I know that of course giving a vision transformer the actual board state like this shortcircuits the cool part where OthelloGPT tries to learn its own representation of the board. But I'm wondering if even in this supposedly easy setting it still would end up imperfect with a tiny error rate and a bag-of-heuristics-like way of computing legal moves.
And brainstorming a bit here: a slightly more interesting setting that might not shortcircuit the cool part would be if the input to the vision transformer was a 3D "video" of the moves on the board. E.g. the input[t][x][y] is 1 if on turn t, a move was made at (x,y), and 0 otherwise. Self-attention would presumably be causally-masked on the t dimension but not on x and y. Would we get a bag of heuristics here in the computation of the board state and the legal moves from that state?
I would guess that it would learn an exact algorithm rather than heuristics. The challenging part for OthelloGPT is that the naive algorithm to calculate board state from input tokens requires up to 60 sequential steps, and it only has 8 layers to calculate the board state and convert this to a probability distribution over legal moves.
What does impossible mean in the context of clock neurons?
impossible in the first few moves.
What causes them to be unable to fire?
In Othello, pieces must be played next to existing pieces, and the game is initialized with 4 pieces in the center. Thus, it's impossible for the top left corner to be played within the first 5 moves, and extremely unlikely in the early portion of a randomly generated game.
The LessWrong Review runs every year to select the posts that have most stood the test of time. This post is not yet eligible for review, but will be at the end of 2025. The top fifty or so posts are featured prominently on the site throughout the year.
Hopefully, the review is better than karma at judging enduring value. If we have accurate prediction markets on the review results, maybe we can have better incentives on LessWrong today. Will this post make the top fifty?
Work performed as a part of Neel Nanda's MATS 6.0 (Summer 2024) training program.
TLDR
This is an interim report on reverse-engineering Othello-GPT, an 8-layer transformer trained to take sequences of Othello moves and predict legal moves. We find evidence that Othello-GPT learns to compute the board state using many independent decision rules that are localized to small parts of the board. Though we cannot rule out that it also learns a single succinct algorithm in addition to these rules, our best guess is that Othello-GPT’s learned algorithm is just a bag of independent heuristics.
Board state reconstruction
Legal move prediction
Review of Othello-GPT
Othello-GPT is a transformer with 25M parameters trained on sequences of random legal moves in the board game Othello as inputs[1] to predict legal moves[2].
How it does this is a black box that we don’t understand. Its claim to fame is that it supposedly
which if true, resolves the black box in two[3].
The evidence for the first claim is that linear probes work. Namely, for each square of the ground-truth game board, if we train a linear classifier to take the model’s activations at layer 6 as input and predict logits for whether that square is blank, “mine” (i.e. belonging to the player whose move it currently is) or “yours”, the probes work with high accuracy on games not seen in training.
The evidence for the second claim is that if we edit the residual stream until the probe’s outputs change, the model’s own output at the end of layer 7 becomes consistent with legal moves that are accessible from the new board state.
However, we don’t yet understand what’s going on in the remaining black boxes. In particular, although it would be interesting if Othello-GPT emergently learned to implement them via algorithms with relatively short description lengths, the evidence so far doesn’t rule out the possibility that they could be implemented via a bag of heuristics instead.
Project goal
Our goal in this project was simply to figure out what’s going on in the remaining black boxes.
Results on box #1: Board reconstruction
A circuit for how the model computes if a cell is blank or not blank
WRT question 1a, we found a mechanistic circuit that Othello-GPT uses to compute if squares are blank or not blank in its internal representation of the board state. The circuit, described here (15p.), is used by Othello-GPT across a test set of 50 games that we looked at, although we didn’t check that Othello-GPT uses it exclusively. The main points are that
An example of a logical rule for how the model computes if a cell is “mine” or “yours”
Wrt question 1b, we conjecture that Othello-GPT computes whether cells are “mine” or “yours” by aggregating many heuristic rules, rather than implementing a crisp algorithm with a short description length. We’ll provide evidence for this claim throughout the post. As a first piece of evidence, we find an example of a logical rule that Othello-GPT appears to implement in layers 0+1 along with a mechanistic explanation of how it does this. The rule and circuit that computes it are described here (10p.). The main points are that
Intra-layer phenomenology
We also studied whether the model internally represents each board square as “blank,” “mine” or “yours” across layers in many sample moves and games, as measured by applying the linear probe to the residual stream in each layer[4]. For example, Figure 1 shows the model’s internally assigned probability that each of the 64 board squares is “yours” at move 14 of game 7[5] (where the legend gives the ground-truth state of each square, and “accessible” squares are adjacent to currently filled squares but not legal).
Across different games and move numbers, this visualization shows that the model frequently up- and down-weights the internal representation of board squares. This is consistent with what we would expect if the model was aggregating a large number of heuristics that are statistically-but-not-always correct (such as the rule that we found above)[6].
Results on box #2: Valid move prediction
Direct logit attribution (Logit Lens)
Direct logit attribution indicates how the prediction of valid moves evolves across layers in the residual stream. Specifically, we apply the unembedding matrix to intermediate activations of the residual stream. Figure 2 shows a typical logit evolution for a particular move in a particular game. We see that the model gradually promotes legal moves and suppresses illegal ones across layers. Accessible squares seem to play a special role, as they tend to have higher logits than other illegal moves. We suspect this is an artifact of the model learning the heuristic “there is a neighboring occupied square to the square considered as a next move”, which is a necessary but not sufficient condition for a move to be legal.
For context, the sufficient rule for valid moves in Othello is that moves to empty squares adjacent to straight or diagonal lines of opponents’ pieces that end with one’s own piece are valid. We’ll call these configurations board patterns from now on. Figure 3 shows three example patterns on the board that make a move on G1 valid.
Board Pattern Neurons
Neel Nanda found that MLP layer 5 has a high causal effect on three adjacent squares in a particular game (see “MLP layer contributions” in his post). Motivated by that, we investigate whether MLP neurons indicate that a pattern is present. We treat MLP neurons as classifiers, resolving in true if the neuron activation during the forward pass is above a threshold.
Indeed, MLP neurons in the second half of the network correspond to groups of patterns. We find 610 neurons that predict the union of patterns with an F1-score > 0.99 across 60k board states. A good predictor for the union of patterns predicts each individual pattern with high recall (the neuron is active if the board state is present) and the union of patterns with high precision (any of the patterns is present if the neuron is active). Figure 4 shows an example of two neurons and the union of board states they predict with high F1. We only consider neurons that correspond to patterns which all promote the same move (note that for a single neuron the green square is always at the same location in Figure 4)[7] and call those board pattern neurons.
There are 1036 board patterns in the game of Othello that are relevant for making a valid move. For each cell on the board, there are 15-18 patterns that make a move on that cell valid. In layer 4, 5, and 6 alone and only restricting to single move neurons, we find that 75.2 % of all patterns are classified by any pattern neuron with an F1-score above 0.99. Relaxing the restriction to all neurons with an F1-score above 0.9, we find 90.6 % of all patterns are classified.
We performed ablations on all pattern neurons to check for causal relevance. For each neuron, we construct a set of games that contain any pattern the neuron corresponds to. Remember, pattern neurons only correspond to a single valid move. We measure the change in probability (after softmax on output logits) for predicting the single move the corresponding patterns make legal, in addition to the change in probability for all other tokens. We don’t find a significant amount of pattern neurons in layers 0-2. In layers 3-6, the ablation changes the probability by an average of -1.5% for the target square, and 0.03% for all other squares on the board. These results suggest that pattern neurons in layers 3-5 predominantly promote legal moves on the associated squares.
Ablating pattern neurons in the final MLP layer 7 greatly increases the probability by an average of 15% for a given square. This indicates that our layer 7 pattern neurons are acting to suppress, not promote, legal moves. In addition to that, the decoder vectors of Layer 7 neurons show almost exclusively a highly negative attribution of below -0.8 to the logit of the corresponding move. We hypothesize that this behavior arises from the implicit training objective to predict a uniform distribution over all legal moves (introduced by training on random legal moves).
Clock Neurons
We observed that a number of neurons fire more based on move number than on which moves were played. We hypothesize that these neurons play a role in upweighting or down weighting the likelihood of tokens based on the time in the game. This is a useful heuristic for predicting valid moves. For example, tokens corresponding to edges and corners are more likely to be legal moves towards the end of the game[8]. It is very rare for these tokens to appear early, and impossible in the first few moves. We find evidence that these neurons are responding to the positional encoding to have a measure of number. Many examples of neurons that fire as a function of move number can be found in Appendix 2 of Jack’s research sprint final report. Clock neurons could be further evidence that Othello-GPT uses a set of probabilistic heuristics to reckon the likelihood of the board state, and of which moves are legal. However, it would be interesting to better understand how they're used by the model.
Suppression behavior
Our anecdotal investigations leave the impression that the heuristic rules encoded in the attention and MLP layers often cancel each other out. Heuristic rules are not always correct individually. So other rules/neurons can come into play that correct the errors. Some of this happens in parallel, so it is not necessarily fair to say that one corrects another. In the big picture, heuristics are adding up such that the probabilities of either valid or invalid eventually overrules the other.
For example, in our discussion of how Othello-GPT computes if a cell is mine vs. yours, the circuit for the logical rule “If A4 is played AND B4 is not blank AND C4 is not blank, update B4+C4+D4 towards “theirs” mistakenly fires if B4 or C4 is “mine” instead of “theirs” . When this happens, the model takes longer to compute the “correct” state of cells B4 + C4, but eventually reaches the right conclusion in later layers. See page 5 of the linked note, especially footnote 4, for more on this point.
Future Work
There are many possible directions for future work. We will follow up by automating the discovery of logical rule circuits and interpretable neurons in Othello-GPT and attempt to reimplement Othello-GPT by hand using the discovered rules[9]. This would add evidence that Othello-GPT computes an internal model of the board as an intermediate representation for legal move prediction.
The “bag of heuristics” hypothesis, if correct, could explain the fact that Othello-GPT is imperfect (i.e., Li et al find an error rate of 0.01%, where the top-1 prediction is actually not a legal move). A follow-up would be to investigate the errors made by Othello-GPT. Perhaps incorrect predictions correspond to rare edge cases that are not handled well by learned heuristics. How does this compare to the processes that lead to hallucinations in other LLMs? It is interesting that even with millions of parameters and thousands of rules, Othello-GPT still makes errors that a simple logical Othello algorithm would not.
Additionally, we are interested in Othello-GPT as a toy model to better understand SAEs or other unsupervised tools for interpretability.
One worry in using Othello-GPT as a toy model is that it may not be representative of a typical LLM. There’s a sense in which Othello-GPT seems much “too large” for the problem that it’s trying to solve, giving it the capacity to memorize many heuristics[10]. Perhaps a smaller model would be forced to learn features in superposition -- or even nontrivial algorithms -- in a way more representative of a typical LLM. So as a final direction, it could be interesting to train transformers of different size on Othello and see how (if) features change as a function of the model size.
Acknowledgements
We thank Sam Marks, Wes Gurnee, Jannik Brinkmann, Lovis Heindrich and Neel Nanda for helpful comments on experiment design and the final post.
As a 1d tensor of moves [‘C3’, ‘C4’, ‘D5’, ‘C6’, …] converted to integer tokens.
As a 2d tensor of shape [seq_len, 61] corresponding to logits for what the model thinks are legal moves at each point in the game.
Humans also do something like this, but resolve box #1 by serially updating their representation of the board on each token in the sequence. LLMs only have num_layers steps of serial computation available so can’t be doing this.
Note that the linear probes were trained on residual layer 6. Perhaps we would get somewhat different results if we trained a new probe for each layer.
The probe output is an (n_board_squares x 3[mine, yours, empty]) tensor. We apply softmax across the dimension [mine, yours, empty], and report the softmax score for 'yours'.
From such visualizations, we also found that although the model mainly finalizes the internal board state around layer 5 and decides which moves are legal in the last two layers, there’s no sharp boundary between the two phases (e.g. the model has some idea which moves are legal if we unembed the residual stream in very early layers).
We observe neurons that have a non-zero activation for every move in every game. They are perfect classifiers for the union of all possible board patterns. To avoid catching these neurons as pattern neurons we filtered for neurons that are good classifiers only for the union of patterns that make a single move valid.
Though perhaps not in the last few moves, when almost every square is filled.
See e.g. the “Artificial artificial neural network” in Curve Circuits.
For example, the same model size can be used to learn chess which has a nearly 10^100x larger game tree.