Wikitag Contributions
Thanks for sharing this, I believe this kind of work is very promising. Especially, it pushes us to be concrete.
I think some of the characteristics you note are necessary side effects of fast parallel computation. Take this canonical constant-depth adder from pg 6 of "Introduction to Circuit Complexity":
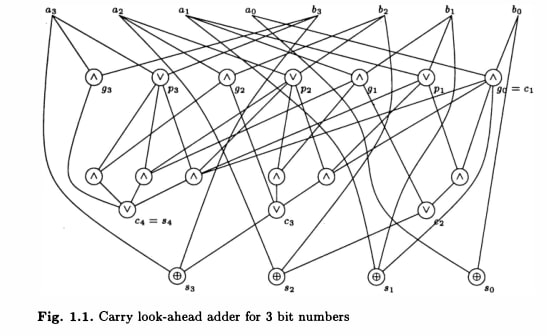
Imagine the same circuit embedded in a neural network. Individual neurons are "merely" simple Boolean operations on the input - no algorithm in sight! More complicated problems often have even messier circuits, with redundant computation or false branches that must be suppressed.
Or imagine a typical program for checking legal moves, some nested for loops. If you actually compile and run such a program you will see the processor perform a long series of local checks. Without the source code any "algorithmness" that remains is in the order those checks are performed in. Now imagine porting that same program to a parallel architecture, like a transformer or the brain. With the checks occurring in parallel there's no obvious systematicity and the whole thing could be mistaken for a mass of unrelated local computations, the algorithm totally obscured. Even more so if the medium is stochastic.
Actually this relates to a problem in circuit complexity - the notion of algorithm itself becomes more subtle. Since circuits are of fixed finite size, they can only accept one size of input. So, in order to solve a task at any size (as Turing machines do) a different circuit is required for each n. But then what's to keep each circuit in the family from being wildly different? How could such an infinitely varied family represent a crisp, succinct algorithm? Besides, this arbitrariness lends a sort of unchecked power, for instance the ability to solve the halting problem! (e.g. by hard coding every answer for each n). To tame this, the notion of "uniform complexity" is introduced. A series of circuits is uniform iff the circuits themselves can be generated by a Turing machine. So an "algorithm" is a finite description of a fast parallel circuit for every size.
This seems like it may apply directly for the case of OthelloGPT. If the list of "heuristics" permit a short generating description, they may indeed represent a crisp algorithm - only implemented in parallel. It would be v. interesting if gradient descent preferred such solutions since the generating rule is only ever implicit. If gradient descent had such a preference it could substitute directly for a more traditional notion of algorithm in many arguments (e.g. about generalization/reasoning/world modeling). Really, any idea of which sort of circuits gradient descent prefers in this case could help illuminate how "deep learning works" at all.
I was trying to make a more specific point. Let me know if you think the distinction is meaningful -
So there are lots of "semi-rigorous" successes in Deep Learning. One I understand better than muP is good old Xavier initialization. Assuming that the activations at a given layer are normally distributed, we should scale our weights like 1/sqrt(n) so the activations don't diverge from layer to layer (since the sum of independent normals scales like sqrt(n)). This is exactly true for the first gradient step, but can become false at any later step once the weights are no longer independent and can "conspire" to blow up the activations anyway. So not a "proof" but successful in practice.
My understanding of muP is similar in that is "precise" only if certain correlations are well controlled (I'm fuzzy here). But still v. successful in practice. But the proof isn't airtight and we still need that last step - checking "in practice".
This is very different from the situation within statistical learning itself, which has many beautiful and unconditional results which we would very much like to port over to deep learning. My central point is that in the absence of a formal correspondence, we have to bridge the gap with evidence. That's why the last part of my comment was some evidence I think speaks against the intuitions of statistical learning theory. I consider Xavier initialization, muP, and scaling laws, etc. as examples where this bridge was successfully crossed - but still necessary! And so we're reduced to "arguing over evidence between paradigms" when we'd prefer to "prove results within a paradigm"
This does a great job of importing and translating a set of intuitions from a much more established and rigorous field. However, as with all works framing deep learning as a particular instance of some well-studied problem, it's vital to keep the context in mind:
Despite literally thousands of papers claiming to "understand deep learning" from experts in fields as various as computational complexity, compressed sensing, causal inference, and - yes - statistical learning, NO rigorous, first-principles analysis has ever computed any aspect of any deep learning model beyond toy settings. ALL published bounds are vacuous in practice.
It's worth exploring why, despite strong results in their own settings, and despite strong "intuitive" parallels to deep learning, this remains true. The issue is that all these intuitive arguments have holes big enough to accommodate, well, the end of the world. There are several such challenges in establishing a tight correspondence between "classical machine learning" and deep learning, but I'll focus on one that's been the focus of considerable effort: defining simplicity.
This notion is essential. If we consider a truly arbitrary function, there is no need for a relationship between the behavior on one input and the behavior on another - the No Free Lunch Theorem. If we want our theory to have content (that is, to constrain the behavior of a Deep Learning system whatsoever) we'll need to narrow the range of possibilities. Tools from statistical learning like the VC dimension are useless as is due to overparameterization, as you mention. We'll need a notion of simplicity that captures what sorts of computational structures SGD finds in practice. Maybe circuit size, or minima sharpness, or noise sensitivity... - how hard could it be?
Well no one's managed it. To help understand why, here are two (of many) barrier cases:
- Sparse parity with noise. For an input bitstring x, y is defined as the xor of a fixed, small subset of indices. E.g if the indices are 1,3,9 and x is 101000001 then y is 1 xor 1 xor 1 = 1. Some small (tending to zero) measurement error is assumed. Though this problem is approximated almost perfectly by extremely small and simple boolean circuits (a log-depth tree of xor gates with inputs on the chosen subset), it is believed to require an exponential amount of computation to predict even marginally better than random! Neural networks require exponential size to learn it in practice.
Deep Learning Fails - The protein folding problem. Predict the shape of a protein from its amino acid sequence. Hundreds of scientists have spent decades scouring for regularities, and failed. Generations of supercomputers have been built to attempt to simulate the subtle evolution of molecular structure, and failed. Billions of pharmaceutical dollars were invested - hundreds of billions were on the table for success. The data is noisy and multi-modal. Protein language models learn it all anyway.
Deep Learning Succeeds!
For what notion is the first problem complicated, and the second simple?
Again, without such a notion, statistical learning theory makes no prediction whatsoever about the behavior of DL systems on new examples. If a model someday outputted a sequence of actions which caused the extinction of the human race, we couldn't object on principle, only say "so power-seeking was simpler after all". And even with such a notion, we'd still have to prove that Gradient Descent tends to find it in practice and a dozen other difficulties...
Without a precise mathematical framework to which we can defer, we're left with Empirics to help us choose between a bunch of sloppy, spineless sets of intuitions. Much less pleasant. Still, here's a few which push me towards Deep Learning as a "computationally general, pattern-finding process" rather than function approximation:
- Neural networks optimized only for performance show surprising alignment with representations in the human brain, even exhibiting 1-1 matches between particular neurons in ANNs and living humans. This is an absolutely unprecedented level of predictivity, despite the models not being designed for such and taking no brain data as input.
- LLM's have been found to contain rich internal structure such as grammatical parse-trees, inference-time linear models, and world models. This sort of mechanistic picture is missing from any theory that considers only i/o
- Small changes in loss (i.e. function approximation accuracy) have been associated with large qualitative changes in ability and behavior - such as learning to control robotic manipulators using code, productively recurse to subagents, use tools, or solve theory of mind tasks.
I know I've written a lot, so I appreciate your reading it. To sum up:
- Despite intuitive links, efforts to apply statistical learning theory to deep learning have failed, and seem to face substantial difficulties
- So, we have to resort to experiment where I feel this intuitive story doesn't fit the data, and provide some challenge cases
Personally, I think approaches like STaR (28 March 2022) will be important: bootstrap from weak chain-of-thought reasoners to strong ones by retraining on successful inner monologues. They also implement "backward chaining": training on monologues generated with the correct answer visible.
The most relevant paper I know of comes out of data privacy concerns. See Extracting Training Data from Large Language Models, which defines "k-eidetic memorization" as a string that can be elicited by some prompt and appears in at most k documents in the training set. They find several examples of k=1 memorization, though the strings appear repeatedly in the source documents. Unfortunately their methodology is targeted towards high-entropy strings and so is not universal.
I have a related question I've been trying to operationalize. How well do GPT-3's memories "generalize"? In other words, given some fact in the training data, how far out of the source distribution can GPT-3 "gain information" from that fact?
E.g. training: "Ixlthubs live in the water." Test: does this affect the predicted likelihood of "Ixlthubs live in the Pacific"? What about "Ixlthubs cannot survive on land"? I'd consider this another interesting measure of sample efficiency/generalization performance. I'm attempting to put together a proposal for the BigScience project (some set of synthetic facts to sprinkle throughout the data), but it's my first try at something like this and slow going.
See also "Evaluating Large Language Models Trained on Code", OpenAI's contribution. They show progress on the APPS dataset (Intro: 25% pass, Comp: 3% pass @ 1000 samples), though note there was substantial overlap with the training set. They also only benchmark up to 12 billion params, but have also trained a related code-optimized model at GPT-3 scale (~100 billion).
Notice that technical details are having a large impact here:
- GPT-3 saw a relatively small amount of code, only what was coincidentally in the dataset, and does poorly
- GPT-J had Github as a substantial fraction of its training set
- The dataset for Google's 137-billion model is not public but apparently "somewhat oversampled web pages that contain code". They also try fine-tuning on a very small dataset (374 items).
- Codex takes a pre-trained GPT-3 model and fine-tunes on 159 GB of code from Github. They also do some light prompt engineering. Overall, they show progress on APPS
- OpenAI's largest model additionally uses a BPE tokenization optimized for code, and may have other differences. It has not yet been publicly benchmarked
There is no state saving or learning at test time. The prompts were prepended to the API calls, you could see it in the requests
I think the appeal of symbolic and hybrid approaches is clear, and progress in this direction would absolutely transform ML capabilities. However, I believe the approach remains immature in a way that the phrase "Human-Level Reinforcement Learning" doesn't communicate.
The paper uses classical symbolic methods and so faces that classic enemy of GOFAI: super-exponential asymptotics. In order to make the compute more manageable, the following are hard-coded into EMPA:
- Direct access to game state (unlike the neural networks, which learned from pixels)
- The existence of walls, and which objects are walls
- The 14 possible object interactions (That some objects are dangerous, that some can be pushed, some are walls, etc)
- Which object is the player, and what type of player (Shooter or MovingAvatar), and which objects are the player's bullets
- The form of the objective (always some object count == 0)
- That object interactions are deterministic
- That picking up resources is good
- The physics of projectile firing: reward was directly transported from a simulation of what a fired projectile hit, obviating the need to plan over that long time horizon
- etc, etc, etc
Additionally, the entire algorithm is tuned to their own custom dataset,. None of this would be feasible for Atari games, or indeed the GVGAI competition, whose video game descriptive language they use to write their own environments. There's a reason they don't evaluate on any of the many existing benchmarks.
I come across a paper like this every once in a while: "The Revenge of GOFAI". Dileep George et al's Recursive cortical networks. Deepmind's Apperception engine. Tenenbaum's own Omniglot solver. They have splashy titles and exciting abstracts, but look into the methods section and you'll find a thousand bespoke and clever shortcuts, feature engineering for the modern age. It's another form of overfitting, it doesn't generalize. The super-exponential wall remains as sheer ever and these approaches simply cannot scale.
I'll reiterate that any progress in these areas would mean substantially more powerful, more explainable models. I applaud these researchers for their work on a hard and important problem. However, I can't consider these papers to represent progress. Instead, I find them aspirational, like the human mind itself: that our methods might someday truly be this capable, without the tricks. I'm left hoping and waiting for insight of a qualitatively different sort.
I think this is a very interesting discussion, and I enjoyed your exposition. However, the piece fails to engage with the technical details or existing literature, to its detriment.
Take your first example, "Tricking GPT-3". GPT is not: give someone a piece of paper and ask them to finish it. GPT is: You sit behind one way glass watching a man at a typewriter. After every key he presses you are given a chance to press a key on an identical typewriter of your own. If typewriter-man's next press does not match your prediction, you get an electric shock. You always predict every keystroke, even before he starts typing.
In this situation, would a human really do better? They might well begin a "proper continuation" after rule 3 only to receive a nasty shock when the typist continues "4. ". Surely by rule 11 a rule 12 is ones best guess? And recall that GPT in its auto-regressive generation mode experiences text in exactly the same way as when simply predicting; there is no difference in its operation, only in how we interpret that operation. So after 12 should come 13, 14... There are several other issues with the prompt, but this is the most egregious.
As for Winograd, the problem of surface associations mimicking deeper understanding is well known. All testing today is done on WinoGrande which is strongly debiased and even adversarially mined (see in particular page 4 figure 1). GPT-3 0-shot scores (70%) well below the human level (94%) but also well above chance (50%). For comparison, BERT (340 million param) 0-shot scores 50.2%.
There are also cases, like multiplication, where GPT-3 unequivocally extracts a deeper "world model", demonstrating that it is at least possible to do so as a language model.
Of course, all of this is likely to be moot! Since GPT-3's release, a primary focus of research has been multimodality, which provides just the sort of grounding you desire. It's very difficult to argue that CLIP, for instance, doesn't know what an avocado looks like, or that these multimodal agents from Deepmind aren't grounded as they follow natural language instructions (video, top text is received instruction).
In all, I find the grounding literature interesting but I remain unconvinced it puts any limits on the capabilities even of the simplest unimodal, unagentic models (unlike, say, the causality literature).
I think the best argument for a "fastest-er" timeline would be that several of your bottlenecks end up heavily substituting against each other or some common factor. A researcher in NLP in 2015 might reasonably have guessed it'd take decades to reach the level of ChatGPT - after all, it would require breakthroughs in parsing, entailment, word sense, semantics, world knowledge... In reality these capabilities were all blessings of scale.
o1 may or may not be the central breakthrough in this scenario, but I can paint a world where it is, and that world is very fast indeed. RL, like next word prediction, is "mechanism agnostic" - it induces whatever capabilities are instrumental to maximizing reward. Already, "back-tracking" or "error-correcting" behavior has emerged, previously cited by LeCun and others as a fundamental block. In this world RL applied to "Chains of Action" strongly induces agentic structures like adaptability, tool use, note caching, goal-directedness, and coherence. Gradient descent successfully routes around any weaknesses in LLMs (as I suspect it does for weaknesses in our LLM training pipelines today). By the time we reach the same engineering effort in post-training that we've dedicated to pretraining, it's AGI. Well, given the scale of OpenAI's investment, we should be able to rule on this scenario pretty quickly.
I'd say I'm skeptical of the specifics (RL hasn't demonstrated this kind of rich success in the past) but more uncertain about the outline (How well could e.g. fast adaptation trade off against multimodality, gullibility, coherence?)