Very nice post, thanks for writing it.
Your options are numbered when you refer to them in the text, but are listed as bullet points originally. Probably they should also be numbered there!
Now we can get down to the actual physics discussion. I have a bag of fairly unrelated statements to make.
-
The "center of mass moves at constant velocity" thing is actually just as solid as, say, conservation of angular momentum. It's just less famous. Both are consequences of Noether's theorem, angular momentum conservation arising from symmetry under rotations and the center of mass thing arising from symmetry under boosts. (i.e. the symmetry that says that if two people fly past each other on spaceships, there's no fact of the matter as to which of them is moving and which is stationary)
-
Even the fairly nailed down area of quantum mechanics in an electromagnetic field, we make a distinction between mechanical momentum (which appears when calculating kinetic energy) and the canonical momentum (for Heisenberg). Canonical momentum has the operator while mechanical momentum is .
-
Minkowski momentum is, I'm fairly sure, the right answer for the canonical momentum in particular. An even faster proof of Minkowski is to just note that the wavelength is scaled by and so gets scaled by a factor of .
-
The mirror experiments are interesting in that they raise the question of what happens when we put an airgap between the mirror and the fluid. If the airgap is large, we get the vacuum momentum, , since the index of refraction for air is nearly 1. If the airgap gets taken to 0, then we're back to . What happens in between?
-
I will say that overall, option 1 looks pretty good to me.
Edit: Removed redundant video link (turned out to already be in original post).
Numbering the options properly is a good idea, done.
To answer your points:
- This is interesting. Symmetry under rotations gives us conservation of angular momentum. Symmetry under translations conservation of linear momentum. You are saying symmetry under boosts gives conservation of centre of mass velocity. Although in "normal" situations (billiard balls colliding) conservation of centre of mass velocity is a special case of as conservation of linear momentum - which I suppose is why I have not heard of it before. I need to look at this more as I find I am still confused. Intuitively I feel like if translation symmetry is doing momentum for us boost symmetry should relate to a quantity with an extra time-derivative in it somewhere.
There is no symmetry under angular boosts, which I imagine is why fly-wheels (or gyroscopes) allow for an "internal reaction drive" for angular velocity. - I did not know that the kinetic and canonical momentum had different values in other fields. That makes option (1) more believable.
- Yes, the k-vector (wavevector) certainly extends by a factor of . So if you want your definition of "momentum" to be linear in wavevector then you are stuck with Minkowski.
I believe, that at the interface between the water and the air we will have a partial reflection of the light. The reflected component of the light has an evanescent tail associated with it that tunnels into the air gap. If we had more water on the other side of the air gap then the evanescent tail would be converted back into a propagating wave, and the light would not reflect from the first water interface in the first place. As the evanescent tail has a length of the order of a wavelength this means that random gaps between the atoms in water or glass don't mess with the propagating light wave, as the wavelength is so much longer than those tiny gaps they do not contribute.
Applying this picture to your question, I think we would expect to interpolate smoothly between the two momentum values as the air gap size was changed, with the interpolation function an exponential with decay distance equal to the length of our evanescent wave.
Thanks for reading. Enjoy your option (1)!
Years ago I heard from someone, roughly, that "optics is no longer science, just a field of engineering, because there are no open questions in optics anymore, we now 'merely' learn the 'science' of optics to become better engineers".
(This was in a larger discussion about whether and how long it would take for anything vaguely similar to happen to "all of physics", and talking about the state of optics research was helpful in clarifying whether or not "that state of seeming to be fully solved" would count as a "fully solved" field for other fields for various people in the discussion.)
In searching just now, I find that Stack Exchange also mentions ONLY the Abraham-Minkowki question as an actual suggestion about open questions in optics... and it is at -1, with four people quibbling with the claim! <3
Thank you for surprising me in a way that I was prepared to connect to a broader question about the the sociology of science and the long run future of physics!
Thank you very much, that sounds like a fascinating wider discussion. Personally, I suspect the Abraham-Minkowski question is only unusual in the sense that it is a known unknown. I think the unknown unknowns are probably much larger in scope. Although it is probably quite dependent on where exactly you draw the physics/engineering boundary.
it is a maximally aggressive violation of the uniform motion of the centre of mass of an isolated system
To me, it seems like this thing you have noticed is an airtight open-and-shut proof. I’m not sure why you’re treating it as merely suggestive.
If the fibre-optic loop (and whatever light is inside it) is in configuration X and time t1, and it’s in the exact same configuration X at time t2, then obviously the time-average momentum of the fibre-optic loop (and whatever light is inside it), over the (t1, t2) interval, is zero, right?
My thoughts on this are not going to be fully coherent, because I am in the process of possibly changing my mind.
I agree that if we take the uniform motion of centre of mass as an absolute principle then the weird light-in-circles machine does not work. However, I had never before encountered this principle, and (to me) it still carries the "I learned about this last week, how much do I trust it?" penalty. But, even accepting it, that doesn't explain why the machine fails. Does it remain the case that the actual mechanical momentum and energy transport directions are opposite in the right metamaterial (as claimed in, for example: https://journals.aps.org/pra/abstract/10.1103/PhysRevA.75.053810 ), but the machine fails for some other reason (eg. recoils on the interfaces)? Showing the machine to be impossible while leaving this unanswered doesn't get to the roots of my various related confusions, I still don't know whether energy flow and momentum can 'really' point opposite directions, or whether it's all just an accounting trick.
The uniform motion of centre of mass implies other things. For example, it means anything like a portal from the game "portal" is impossible as the centre of mass would change discontinuously as something went through the portal. [We can even "re-skin" of the photon loop by instead having a train with portals, so it can keep reusing the same track on our space ship repeatedly].
I agree that you can confidently believe that something won’t work because of some high-level principle, but still be curious for a nuts-and-bolts lower-level explanation of why it doesn’t work. That’s a perfectly healthy and fun and pedagogical activity. A classic example is questions in the genre “Why does this particular proposal for a perpetual machine not actually work?” Another is “What’s the flaw in this apparent proof that 0=1?”
I was just saying that we should be confident about the high-level principle here, not that there’s anything wrong with being curious about the thing that you’re curious about. :)
I agree that if we take the uniform motion of centre of mass as an absolute principle then the weird light-in-circles machine does not work. However, I had never before encountered this principle, and (to me) it still carries the "I learned about this last week, how much do I trust it?" penalty.
Start from the fact that the fundamental laws of physics are the same regardless of where you are. Then Noether’s theorem gets us from there to conservation of momentum. And then conservation of momentum implies uniform motion of the center of mass, right? (I think that second step involves spatial integration to get from a local continuity equation to a global conservation law, and so general relativity might or might not mess up that part, not sure. But anyway, we’re assuming flat space here.)
"And then conservation of momentum implies uniform motion of the center of mass, right?" - This is the step I am less than 100% on. Certainly it does for a collection of billiard balls. But, as soon as light is included things get less clear to me. It has momentum, but no inertial mass. Plus, as an admittedly weird example, the computer game "portal" has conservation or momentum, but not uniform motion of the centre of mass. Which means at the very least the two can logically decouple.
Plus, as an admittedly weird example, the computer game "portal" has conservation or momentum, but not uniform motion of the centre of mass. Which means at the very least the two can logically decouple.
That's related to what I wrote here:
I think that second step involves spatial integration to get from a local continuity equation to a global conservation law, and so general relativity might or might not mess up that part, not sure. But anyway, we’re assuming flat space here.
The spatial integration step, to get from local properties (continuity equation for momentum density) to global properties (center of mass motion), can get screwed up by weird topology (e.g. teleportation portals), just like it can get screwed up by curved spacetime. You do have to assume that spacetime is normal flat Minkowski space.
Certainly it does for a collection of billiard balls. But, as soon as light is included things get less clear to me. It has momentum, but no inertial mass.
Maybe this link is a proof? It kinda looks right but I didn’t check it super-carefully. It uses the stress-energy tensor which applies to both matter and electromagnetic waves. Note the part where they integrate over space and set the boundary term at infinity to zero—that part doesn’t work with curved space or wormholes.
It's also trivial to make a perpetual motion machine with Portal portals. Just have a portal in the floor that teleports you to the ceiling directly above it, then drop a ball into it. It'll fall forever, accelerating until it hits terminal velocity (at which point all the gravitational potential energy goes to heating the air it falls through).
If you don't want to just throw out conservation of energy, using a portal to "lift" things would have to take the same amount of energy as lifting it through normal space does.
Yes, you could fix it by making the portal pay for lifting. An alternative fix would be to let gravity go through portals, so the ball feels the Earth's gravity by the direct route and also through the portal. Which I think makes the column between the two portals zero G, with gravity returning towards normal as you move radially. This solution only deals with the steady-state though, at the moment portals appear or disappear the gravitational potential energy of objects (especially those near the portal) would step abruptly.
Its quite a fun situation to think about.
As far as I understand, "a photon in a medium" is a quasiparticle. Actual photons always travel at the speed of light, and the "photon" that travels through glass at a lower speed is the sum of an incredibly complicated process that cancels out perfectly into something that can be described as one or several particles if you squint a little because the energy of the electromagnetic field excitation can't be absorbed by the transparent material and because of preservation of momentum.
The model of the photon "passing by atoms and plucking them" is a lie to children, an attempt to describe a quantum phenomenon in classically comprehensible terms. As such, what "the momentum of the quasiparticle" is depends on what you consider to be part of the quasiparticle, or which parts of the quasiparticle(s) you measure when doing an experiment.
Specifically, for the mirror-in-a-liquid, when light hits the liquid it is refracted. That refraction makes the angle of the path of the light more steep, which means the mirror has to reflect momentum that is entering at a more steep angle, and so the momentum the mirror measured is multiplied by the refractive index. At the quasiparticle level, when hitting the liquid interface, the light interacts with the quasiparticle phonon [sic] field of the liquid, exchanging momentum to redirect the quasiparticle light, and the mirror has to reflect both the quasiparticle light and the phonon field, resulting in the phonons being included with "the momentum of the light".
However, for the light-through-a-glass-fiber, you are measuring the momentum of the phonons as part of the not-light, because the phonons are part of the medium, so part of the glass fiber getting nudged by the light beam.
I'm not sure how this works out in rigorous calculation, but this is my intuition pump for a [1]-ish answer.
Yes, you are certainly right it is a quasiparticle. People often use the word polariton to name it (eg https://www.sciencedirect.com/science/article/pii/S2666032620300363#bib1 ).
I think you might have muddled the numbering? It looks like you have written an argument in favor of either [2] or [3] (which both hold that the momentum of the full polariton is larger than the momentum of the photonic part alone - in the cartoon of the original post whether or not the momentum "in the water" is included), then committed to [1] instead at the end. This may be my fault, as the order I numbered the arguments in the summary at the end of the post didn't match the order they were introduced, and [2] was the first introduced. (In hindsight this was probably a bad way to structure the post, sorry about that!)
" "passing by atoms and plucking them" is a lie to children " - I personally dislike this kind of language. There is nothing wrong with having mental images that help you understand what is going on. If/when those images need to be discarded then I don't think belittling them or the people who use them is helpful. In this case the "plucking" image shows that at any one time some of the excitation is in the material, which is the same thing you conclude.
[In this case I think the image is acceptably rigorous anyway, but lets not litigate that because which mental images are and are not compatible with a quantum process is a never ending rabbit hole.]
Thank you very much for reading and for your thoughts. If I am correct about the numbering muddle it is good to see more fellow [2/3]'ers.
I have such a strong intuitive opposition to the Internal Reaction Drive that I agree with your conclusion that we should update away from any theory which allows it. Then again, perhaps it is impossible to build such a drive for the merely practical reason that any material with a positive or negative index of refraction will absorb enough light to turn the drive into an expensive radiator.
Especially given the recent Nobel prize announcement, I think the most concerning piece of information is that there are cultural forces from within the physics community discouraging people from trying to answer the question at all.
Abraham was a complete hack who never got anything right in his whole career
I like this quote about him, by Born and von Laue in his obituary, which might be saying the same thing but more poetically:
He loved his absolute aether, his field equations, his rigid electron, just as a youth loves his first flame, whose memory no later experience can extinguish.
Note however, that the principle being broken (uniform motion of centre of mass) is not at all one of the "big principles" of physics, especially not with the extra step of converting the photon energy to mass. I had not previously heard of the principle, and don't think it is anywhere near the weight class of things like momentum conservation.
I found these sentences surprising. To me, the COM moving at constant velocity (in an inertial frame) is Newton's first law, which is one of the big principles (and I also have a mental equality between that and conservation of momentum).
I guess we can also reach your conclusion in that thought experiment arguing from conservation of momentum directly (though I guess the argument I'll give just contains a proof of one direction of the equivalence to the conservation of momentum as a step). Ignoring relativity for a second, we could go into the center of mass frame as the particle approaches the piece of glass from the left, then note that the momentum in this frame needs to zero forever (by conservation of momentum), then note $\int p \text{d}t=m\delta(x)$, where $\delta(x)$ is the distance moved by the center of mass, from which $\delta(x)=0$. I would guess that essentially the same argument also works when relativistic things like photons are involved (and when fields or quantum stuff is involved), as long as one replaces the center of mass by the center of energy ( https://physics.stackexchange.com/questions/742770/centre-of-energy-in-special-relativity ).
One thing that worries me about that thought experiment more than [whether Newton's first law carries over to this context] is the assumption that (in ideal conditions) photons do not lose any energy to the material — that they don't end up redshifted or something. (If photons got redshifted as they go through, then the photons would lose some energy and the block would end up with some momentum and heat, obviously causing issues with the broader argument.) Still, I guess it's probably fine to say that frequency/energy of the light is indeed conserved ( https://physics.stackexchange.com/questions/810869/why-does-the-energy-and-thus-frequency-of-a-photon-entering-glass-stay-constan ), but I unfortunately don't atm understand how to think about a light packet (or something) going through a (potentially moving) material well enough to decide for myself atm. (ChatGPT tells me of some standard argument involving the displacement field, but I haven't decided if I'll trust that argument in this context yet. I also tried to see whether such an effect would be higher-order in some parameter even if it existed but I didn't see a good reason why that would be the case.)
A second thing that worries me about this argument even more is whether it even makes sense to talk about individual photons passing through materials — I think the argument doesn't make sense if photon number is not conserved before vs after a light pulse enters a material (here I'm thinking of the light pulse having small horizontal extent compared to the material). But I really haven't thought very carefully about this. (Also, I'd like to point out that if some kind of light packet number were conserved and we are operating with a notion of momentum such that all of it can be attributed to wave packets, then momentum conservation implies the momentum attributed to a given packet stays constant. But I guess some of it might be more naturally attributed to stuff in the block at some point. I'd need to think more about what kind of partition would be most natural.)
I consider momentum conservation a "big principle.", and Newtons 3 laws indeed set out momentum conservation. However, I believe uniform centre of mass motion to be an importantly distinct principle. The drive loop thing would conserve momentum even if it were possible. Indeed momentum conservation is the principle underpinning the assumed reaction forces that make it work in the first place. To take a different example, if you had a pair of portals (like from the game "portal") on board your spaceship, and ran a train between them, you could drive the train backwards, propelling your ship forwards, and thereby move while conserving total momentum, only to later put the train's breaks on and stop. I am not asking you to believe in portals, I am just trying to motivate that weird hypotheticals can be cooked up where the principle of momentum conservation decouples from the principle of uniform centre of mass motion. The two are distinct principles.
Abraham supporters do indeed think you can use conservation of momentum to work out which way the glass block moves in that thought experiment, showing that (because the photon momentum goes down) the block must move to the right. Minkowksi supporters also think you can use conservation of momentum to work out how the glass block moves, but because they think the photon momentum goes up the block must move to the left. The thing that is at issue is the question of what expression to use to calculate the momentum, both sides agree that whatever the momentum is it is conserved. As a side point, a photon has nonzero momentum in all reference frames, and that is not an aspect of relativity that is sensibly ignored.
You are actually correct that the photon does have to red-shift very slightly as it enters the glass block. If the glass was initially at rest, then after the photon has entered the photon has either gained or lost momentum (depending on Abraham or Minkowski), in either case imparting the momentum difference onto the glass block. The kinetic energy of the glass block is given by where p is the momentum the block has gained, and m is the block's mass. The photon's new frequency is then given by (by conservation of energy) where was its initial frequency. In practice a glass block will have a very gigantic mass compared to , but at least in principle the photon does red shift.
Going into the full gory detail for Abraham.
Abraham:
Photon momentum before entering glass
Photon momentum after entering glass (note, new frequency , not the old one)
Change in photon momentum
The same momentum goes into the glass, so
We can re-arrange to put the c^2 in the denominator next to the mass of the glass block. So that the change in the frequency/energy of the photon is scaled by a term that has something to do with the refractive index, along with how the photon energy compares to the rest mass energy of the glass block (). So, as previously said, this is negligible for a glass block that weighs any reasonable amount.
The Minkowski version is almost the same derivation, except the division by refractive index becomes a multiplication, giving:
Playing with these quadratic equations, to solve for , you find that the Abraham version never breaks. In contrast, if you assume it is possible to have a glass block with a reasonably high refractive index, but arbitrarily small mass, then Minkowski eventually breaks and starts giving an imaginary frequency. This maybe says something vaguely negative about Minkowski, but a block of material with a high refractive index but negligible mass is such an unrealistic setup that I don't think failing in that case is too embarrassing for the Minkowski equation.
here's a picture from https://hansandcassady.org/David%20J.%20Griffiths-Introduction%20to%20Electrodynamics-Addison-Wesley%20(2012).pdf :
Given 12.72, uniform motion of the center of energy is equivalent to conservation of momentum, right? P is const <=> dR_e/dt is const.
(I'm guessing 12.72 is in fact correct here, but I guess we can doubt it — I haven't thought much about how to prove it when fields and relativistic and quantum things are involved. From a cursory look at his comment, Lubos Motl seems to consider it invalid lol ( in https://physics.stackexchange.com/a/3200 ).)
That said, the hypothetical you give is cool and I agree the two principles decouple there! (I intuitively want to save that case by saying the COM is only stationary in a covering space where the train has in fact moved a bunch by the time it stops, but idk how to make this make sense for a different arrangement of portals.) I guess another thing that seems a bit compelling for the two decoupling is that conservation of angular momentum is analogous to conservation of momentum but there's no angular analogue to the center of mass (that's rotating uniformly, anyway). I guess another thing that's a bit compelling is that there's no nice notion of a center of energy once we view spacetime as being curved ( https://physics.stackexchange.com/a/269273 ). I think I've become convinced that conservation of momentum is a significantly bigger principle :). But still, the two seem equivalent to me before one gets to general relativity. (I guess this actually depends a bit on what the proof of 12.72 is like — in particular, if that proof basically uses the conservation of momentum, then I'd be more happy to say that the two aren't equivalent already for relativity/fields.)
I think the point about angular momentum is a very good way of gesturing at how its possibly different. Angular momentum is conserved, but an isolated system can still rotate itself, by spinning up and then stopping a flywheel (moving the "center of rotation").
Thank for finding that book and screenshot. Equation 12.72 is directly claiming that momentum is proportional to energy flow (and in the same direction). I am very curious how that intersects with claims common in metamaterials (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.75.053810 ) that the two can flow in opposite directions.
In my post the way I cited Lubos Motl's comment implicitly rounded it off to "Minkowski is just right" (option [6]), which is indeed his headline and emphasis. But if we are zooming in on him I should admit that his full position is a little more nuanced. My understanding is that he makes 3 points:
(1) - Option [1] is correct. (Abraham gives kinetic momentum, Minkowski the canonical momentum)
(2) - In his opinion the kinetic momentum is pointless and gross, and that true physics only concerns itself with the canonical momentum.
(3) - As a result of the kinetic momentum being worthless its basically correct to say Minkowski was "just right"(option [6]). This means that the paper proposing option [1] was a waste of time (much ado about nothing), because the difference between believing [1] and believing [6] only matters when doing kinetics, which he doesn't care about. Finally, having decided that Minkowski was correct in the only way that he thinks matters, he goes off into a nasty side-thing about how Abraham was supposedly incompetent.
So his actual position is sort of [1] and [6] at the same time (because he considers the difference between them inconsequential, as it only applies to kinetics). If he leans more on the [1] side he can consider 12.72 to be valid. But why would he bother? 12.72 is saying something about kinetics, it might as well be invalid. He doesn't care either way.
He goes on to explicitly say that he thinks 12.72 is invalid. Although I think his logic on this is flawed. He says the glass block breaks the symmetry, which is true for the photon. However, the composite system (photon + glass block) still has translation and boost symmetry, and it is the uniform motion of the center of mass of the composite system that is at stake.
re redshift: Sorry, I should have been clearer, but I meant to talk about redshift (or another kind of energy loss) of the light that comes out of the block on the right compared to the light that went in from the left, which would cause issues with going from there being a uniformly-moving stationary center of mass to the conclusion about the location of the block. (I'm guessing you were right when you assumed in your argument that redshift is 0 for our purposes, but I don't understand light in materials well enough atm to see this at a glance atm.)
And the loss mechanism I was imagining was more like something linear in the distance traveled, like causing electrons to oscillate but not completely elastically wrt the 'photon' inside the material.
Anyway, in your argument for the redshift as the photon enters the block, I worry about the following:
- can we really think of 1 photon entering the block becoming 1 photon inside the block, as opposed to needing to think about some wave thing that might translate to photons in some other way or maybe not translate to ordinary photons at all inside the material (this is also my second worry from earlier)?
- do we know that this photon-inside-the-material has energy ?
The microscopic picture that Mark Mitchison gives in the comments to this answer seems pretty: https://physics.stackexchange.com/a/44533 — though idk if I trust it. The picture seems to be to think of glass as being sparse, with the photon mostly just moving with its vacuum velocity and momentum, but with a sorta-collision between the photon and an electron happening every once in a while. I guess each collision somehow takes a certain amount of time but leaves the photon unchanged otherwise, and presumably bumps that single electron a tiny bit to the right. (Idk why the collisions happen this way. I'm guessing maybe one needs to think of the photon as some electromagnetic field thing or maybe as a quantum thing to understand that part.)
I presented the redshift calculation in terms of a single photon, but actually, the exact same derivation goes through unchanged if you replace every instance of with and with . Where and are the energy of a light pulse before and after it enters the glass. There is no need to specify whether the light pulse is a single photon a big flash of classical light or anything else.
Something linear in the distance travelled would not be a cumulatively increasing red shift, but instead an increasing loss of amplitude (essentially a higher cumulative probability of being absorbed). This is represented using a complex valued refractive index (or dielectric constant) where the real part is how much the wave slows down and the imaginary part is how much it attenuates per distance. There is no reason in principle why the losses cannot be arbitrarily close to zero at the wavelength we are using. (Interestingly, the losses have to be nonzero at some wavelength due to something called the Kramers Kronig relation, but we can assume they are negligible at our wavelength).
Related: In mathematics, people are similarly labeled "cranks" when they disagree with today's consensus over certain foundational assumptions involving set theory and infinity. E.g. Cantor's diagonal argument. This attitude is toxic, because it isn't just saying "He is wrong" but "He is a crackpot, shun him!" It's a toxic way of silencing dissent.
Diagonal argument is not an assumption. You can, of course, disagree with any of the assumptions it relies on, and some mathematicians do so.
Some reject the axiom of infinity, and the use of actual infinities in general. Others reject the axiom schema of specification, or rather put some limits on the formulas it can be used with. (There may be other objections I haven't heard of.) These are not referred to as crackpots. They are choosing a different collection of axioms -- i.e. their "sets" are not the same as Cantor's "sets" -- and they can show the exact step where Cantor's diagonal argument fails to apply in their system.
I think the label crackpot is applied to people who vocally disagree with the argument, but can't pinpoint the place where it fails; in other words they have a strong opinion on something they don't understand.
.
I also think it's fair to say "I disagree with the conclusions of Cantor's diagonal argument, although I can't explain where exactly it fails, because these things are too abstract for me -- it's just that the outcome feels wrong according to my intuition, so there is probably a step I would disagree with, even if I can't tell which one it is".
Such people might even be happy to learn about Skolem's paradox, which used to drive "the opposite camp" crazy. "There are countable models of ZF set theory that satisfy the theorem that there are uncountable sets." -- which at first sight seems like absolute nonsense, but it's a logical consequence of following the axioms.
Nonetheless, modern set theorists are okay with this, too. So the problem is not with disagreeing with the outcomes per se, but with not being able to play the game according to its rules.
Let me explain. I get the following impression. When making basically any other argument in philosophy of mathematics, people are generally highly disinterested, but as soon as the debate touches on issues involving transfinite set theory, like diagonalization, at least people online (on blogs, Wikipedia, Stack Exchange etc, though journals might be similar) are quick to heavily downvote comments and declare people to be "fringe" or "cranks". Even though they have opinions that were completely mainstream until a hundred years ago, and were defended by a number of well-known mathematicians and respectable philosophers like Wittgenstein.
To give a more specific example: Adding a "criticism" or "controversy" section to certain Wikipedia articles on topics around infinity in set theory seems almost as impossible as writing a Wikipedia article covering certain taboo research involving race and IQ.
The only way to argue in a different direction is to word things very carefully and conservatively to not step outside the narrow Overton window. Optimally one shouldn't be directly arguing for anything and instead just engage in explaining arguments other respectable people like Weyl or Wittgenstein have hopefully already made. Failing that, one should always introduce statements with hedges like "From the perspective of finitism, (diagonalization / ...) is of questionable validity because..." However, just saying directly "(Diagonalization / ...) is of questionable validity because..." is seen as beyond the pale, cranky, or otherwise unacceptable.
I think the reason for these hostilities is that in these disagreements there is an implicit battle going on over where to draw the line between mathematics (the land of definitive facts) and philosophy of mathematics (where nothing is certain and diverse positions may be defended). The reason why hedging a statement with "from the perspective of finitism, ..." makes it more acceptable, is that this phrase places it in the realm of philosophy, where things may be questioned.
For example, in mathematics land, two sets have the same size iff there is a definable one-to-one correspondence. Full stop. Anyone who disagrees is a flat-Earther.
But in philosophy-of-mathematics land, this same thesis is called Hume's principle. When referred to by this name, disagreement is suddenly very much allowed. Not only that, the principle is generally seen as resting on a somewhat shaky ground, or anyway being in need of further justification. The only reason these two inconsistent perspectives on the same topic can co-exist in Wikipedia is that they simply don't acknowledge each other. But if someone were to propose to merge the articles, the philosophy perspective would likely lose.
Regarding these points:
Diagonal argument is not an assumption. You can, of course, disagree with any of the assumptions it relies on, and some mathematicians do so.
I'm really not aware of any assumptions one can disagree with here while still being perceived as respectable. The most one can say is something like "Finitists might argue that given any way to construct the infinite table, the rows must approach infinity faster than the columns, in which case the diagonal number is always on the table" or something like that. But even this would be suspect and in any case not constitute a specific assumption one is permitted to disagree with.
Some reject the axiom of infinity, and the use of actual infinities in general.
But these assumptions are only directly related to Cantor's power set argument ("Cantor's theorem"), which is different from his diagonal argument. The former involves (power) sets, the latter real numbers. The latter is also not directly related to Skolem's paradox.
There is a "Controversy over Cantor's theory" article in Wikipedia. Plus articles on finitism, etc.
opinions that were completely mainstream until a hundred years ago, and were defended by a number of well-known mathematicians and respectable philosophers like Wittgenstein.
Some respected scientists of the past have defended elan vital or aether. And yet, if someone did the same today, they wouldn't get any respect for that. One could say that elan vital and aether are now outside the Overton window, but there are good reasons for that.
one should always introduce statements with hedges like "From the perspective of finitism, (diagonalization / ...) is of questionable validity because..." However, just saying directly "(Diagonalization / ...) is of questionable validity because..." is seen as beyond the pale, cranky, or otherwise unacceptable.
Well yes, if you use different axioms, you get different results. Using axioms X, Y, Z, statement S is true; using axioms A, B, C, statement S is false. So if there is an article explaining how XYZ implies S, saying "however, from the perspective ABC, S is false" makes sense, but saying merely "however, S is false" is confusing. Are you saying that XYZ does not imply S? That would be wrong. Or are you saying that you disagree with XYZ and we should use ABC instead? Then say it clearly.
If you want to argue that two sets that have a 1:1 correspondence do not have the same size, start by saying what you actually mean by "size"? (Do you see the repeating pattern here? It is the unclear argumentation that is often a problem. Not merely disagreeing with some definition, but using words in an unusual way without bothering to explain that. Perhaps without even being aware that different definitions can lead to different outcomes.) You can successfully argue that a 2-inch line does not have the same size as a 1-inch line, but you have to make it clear that you are talking about length rather than about cardinality.
But these assumptions [axiom of infinity] are only directly related to Cantor's power set argument ("Cantor's theorem"), which is different from his diagonal argument.
The diagonal argument assumes that you write down the real numbers. But how could you write down the decimal representation of 1/3, if you are not allowed to use infinitely many 3's? More importantly, what are you going to do about uncomputable numbers, if you can neither provide the algorithm that returns the digits on demand, nor assume that the infinite sequence of their digits simply exists?
So now you are making a list of computable numbers (or something like that) rather than the list of real numbers. And Cantor's diagonal argument still finds a number that was not included in the original list.
There is a "Controversy over Cantor's theory" article in Wikipedia.
Well, just read the introduction. It says nothing about the controversy and instead presupposes that Cantor is correct:
Cantor's theorem implies that there are sets having cardinality greater than the infinite cardinality of the set of natural numbers.
That is, the introduction asserts that Cantor's power set argument is correct and doesn't mention any criticisms, despite the title of the article. Even later it mentions Skolem nowhere, nor any criticism of the diagonal argument. Absurdly enough, the article neutrality header even claims that the article is biased in the anti-Cantor direction, when clearly the opposite is the case.
Plus articles on finitism, etc.
Yes, as I said previously: Under the term "finitism" these positions are allowed, because this places them merely in the philosophy of mathematics bin, but not in mathematics articles in general.
Some respected scientists of the past have defended elan vital or aether. And yet, if someone did the same today, they wouldn't get any respect for that. One could say that elan vital and aether are now outside the Overton window, but there are good reasons for that.
This analogy is inappropriate. Finitism is not like élan vital. In fact, finitism doesn't say anything specific (like élan vital or aether) exists, but that something doesn't exist (or isn't required to assume to exist), namely the actual infinite. And it is hardly the case that infinitism is a scientific fact now while finitism is disproved. So finitism is nothing like the examples you gave; finitists today are not cranks like defenders of élan vital would be. Or do you think otherwise?
Well yes, if you use different axioms, you get different results. Using axioms X, Y, Z, statement S is true; using axioms A, B, C, statement S is false. So if there is an article explaining how XYZ implies S, saying "however, from the perspective ABC, S is false" makes sense, but saying merely "however, S is false" is confusing. Are you saying that XYZ does not imply S? That would be wrong. Or are you saying that you disagree with XYZ and we should use ABC instead? Then say it clearly.
If only it were that simple. It is not clear what axioms Cantor's diagonal argument uses. It is largely informal. Which axioms do you think it relies on?
If you want to argue that two sets that have a 1:1 correspondence do not have the same size, start by saying what you actually mean by "size"?
That's not the relevant question. The question is what we (humans in general) commonly mean with something being infinite. Finitists say potential infinity (or unboundedness) is the answer, infinitists say we mean something stronger. There are various arguments for and against, and that's precisely the disagreement between finitism and infinitism. In the case of potential infinity, size comparisons are done via comparisons of rates of growth of sequences, not via mappings between unordered sets. Two quantities have the same size if they "approach infinity" at the same rate. This notion of size is used all the time in calculus. (Which has the distinction of having a lot of real world applications, unlike transfinite set theory.) And it doesn't introduce new exotic properties, like that a proper subset can have the same "size" as the original set, which never happens for finite quantities.
You can successfully argue that a 2-inch line does not have the same size as a 1-inch line, but you have to make it clear that you are talking about length rather than about cardinality.
This doesn't answer the question of whether it makes more sense to call a line with "infinite" length "unboundedly long" or "of actual infinite (countable? uncountable?) length". I would argue the former makes sense, the latter doesn't, because it isn't clear what "countably infinite length", or the like, would mean.
But these assumptions [axiom of infinity] are only directly related to Cantor's power set argument ("Cantor's theorem"), which is different from his diagonal argument.
The diagonal argument assumes that you write down the real numbers. But how could you write down the decimal representation of 1/3, if you are not allowed to use infinitely many 3's? More importantly, what are you going to do about uncomputable numbers, if you can neither provide the algorithm that returns the digits on demand, nor assume that the infinite sequence of their digits simply exists?
The axiom of infinity is only about actual infinity. It is not required for potential infinity. Even without the axiom of infinity, there is no largest set with some finite size. Finitism, despite its (misleading) name, doesn't say there are no infinities, it just disagrees with infinitism about the meaning of "infinite", as I emphasized above. So infinite decimal expansions are not ruled out. (The actual rejection of any infinite quantities is called ultrafinitism.)
So now you are making a list of computable numbers (or something like that) rather than the list of real numbers. And Cantor's diagonal argument still finds a number that was not included in the original list.
Why? Cantor assumes we have an infinite table of decimal digits. Under finitism, this means both the number of columns and rows are "infinite", that is, they are unbounded, they grow without bound. The diagonal number would only not be on the table if the number of columns grows at least as fast as the number of rows. Which wouldn't be the case for a lexicographic ordering. E.g. for base 10, if the number of columns/digits grows with , the number of rows grows with . So for any rectangular table, the diagonal number is on the table, for any . The table is only square for the unary number system, but with those the diagonal argument doesn't work in the first place, as no digits can be swapped.
I'll try to rephrase it as I understood it (the objection against the diagonal argument):
.
Actual infinities do not exist. We only have sequences that can be extended without limits.
If you see the diagonal not as a finished object, but as a sequence that keeps growing, then for any (finite) length of that diagonal (i.e. what an infinitist would call a "prefix" of the diagonal), you can find a row, usually much lower in the table, that actually contains the negation of that (unfinished) sequence. ("Negation" = when you change every digit to something different.)
That is, yes you can have a(n unfinished) table that contains the negation of its own (every unfinished part of) diagonal.
.
My issue with this answer is that you seem to say "this table contains the negation of its own diagonal", but then you keep changing your mind about where exactly it is. Like, at the moment we only get five columns, you can point at a row 678 and say "this row contains the negation of the diagonal (so far)". But when we later get to 678 columns, and obviously the digit at [678, 678] cannot be a negation of itself, you say "actually, it is the row 123456789 that contains the negation of the (first 678 digits of) the diagonal". And of course, once we get to 123456789 columns, you will have to change your mind again. And again.
So it's like... the negation of the diagonal supposedly is there, but... not at any specific place?
.
Also, if we say that actual infinities are not real, then what are we actually trying to prove by the diagonal argument? That real numbers between 0 and N grow faster than integers between 0 and N? That the number of all subsets of N items grows faster than N? Those statements still seem true to me.
So it’s like… the negation of the diagonal supposedly is there, but… not at any specific place?
Why should this be a problem? On this view, there is no “the diagonal”; there are only diagonals of particular tables for particular values of n, which each have their own negations.
I guess one could similar argue that there is no "the table"; there are only finite tables that are gradually expanded rightwards and downwards... and whether they contain their anti-diagonals, that kinda depends on whether they expand downwards much faster than they expand rightwards.
There are probably other strange consequences, such as inability to say whether two real numbers are equal or not; all you can say is "so far, the digits I have checked do match", but by that logic π actually equals 22/7, at least at the beginning; and 3×(1/3) could or count not be 1, no one knows.
And the question of whether there are more real numbers than integers reduces to "there is only a finite amount of each already written, so it depends on whether the guy who writes down the real numbers is faster than the guy who writes down the integers". Does this resemble the math as we know it?
If someone bites the bullet and says "yeah, the math where you can't figure out how much is 3×(1/3) is philosophically preferable to math with infinities (because infinities do not really exist in nature, and frankly neither does perfect equality)", I can respect that. But I would like people to say all of that up front, rather than hide behind "but there are problems with Cantor's definition". There are problems with every definition, you just have to pick your poison.
The bullet-biting here is just “‘real numbers’ are fake”. That makes most of the questions you cite moot.
What are real numbers then? On the standard account, real numbers are equivalence classes of sequences of rationals, the finite diagonals being one such sequence. I mean, "Real numbers don't exist" is one way to avoid the diagonal argument, but I don't thinks that's what cubefox is going for.
consensus over certain foundational assumptions involving set theory and infinity.
Are you referring to things like the Axiom of Choice (which is obviously true), the well-ordering principle (obviously false), and Zorn's lemma (who can say)?
Yeah, that stuff is weird.
1(The joke here is that, given the other axioms of ZF set theory, each of these three things can be used to prove the other two - they're either all true or all false, regardless of how plausible or implausible they might seem on their own.)
Another analogy is with a ball rolling on two surfaces crossing the boundary. The first very little friction, then second a bit more.
From AI:
"The direction in which the ball veers when moving from a smooth to a rough surface depends on several factors, especially the initial direction of motion and the orientation of the boundary between the two surfaces. Here’s a general outline of how it might behave:
- If Moving at an Angle to the Boundary:
- Suppose the ball moves diagonally across the boundary between the smooth and rough surfaces (i.e., it doesn’t cross perpendicularly).
- When it hits the rough surface, frictional resistance increases more on the component of motion along the boundary line than on the perpendicular component.
- This causes the ball to veer slightly toward the rougher surface, meaning it will change direction in a way that aligns more closely with the boundary.
This is similar to a light ray entering water. So is the physics the same? (on second reading, its not so clear, if you put a golf ball from a smooth surface to a rough one, what happens to the angle at the boundary?)
Well in this case, the momentum of the ball clearly won't increase, instead it will be constantly losing momentum and if the second surface was floating it would be pushed so as to conserve momentum. Unlike for light however if it then re-enters the smooth surface it will be going slower. It seems the ball would lose momentum at both transition boundary. (however if the rough surface was perfectly floating, then perhaps it would regain it)
Anyway for a rough surface that is perfectly floating, it seems the ball gives some momentum to the rough surface when it enters it, (making it have velocity) then recovers it and returns the rough surface to zero velocity when it exits it. In that case the momentum of the ball decreases while travelling over the rough surface.
Not trying to give answers here, just add to the confusion lol.
1I read about better analogy long time ago: use two wheels on an axle instead of single ball, then refraction come out naturally. Also I think instead of difference in friction it is better to use difference in elevation, so things slow down when they go to an area of higher elevation and speed back up going down.
Yes that does sound better, and is there an equivalent to total internal refraction where the wheels are pushed back up the slope?
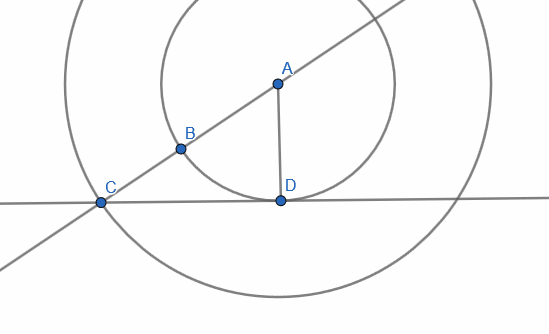
I tried to derive it, turned out to be easy: BC is wheel pair, CD is surface, slow medium above. AC/Vfast=AB/Vslow and for critical angle D touches small circle (inner wheel is on the verge of getting out of medium) so ACD is right triangle, so AC*sin (ACD)= AD (and AD same as AB) so sin(ACD) = AB/AC= Vslow/Vfast. Checking wiki it is the same angle (BC here is wavefront so velocity vector is normal to it). Honestly I am a bit surprised this analogy works so well.
Cool, that was my intuition. GPT was absolutely sure in the golf ball analogy however that it couldn't happen. That is the ball wouldn't "reflect" off the low friction surface. Tempted to try and test somehow
I think that most people underestimate how many scientific mysteries remain, even on questions that sound basic.
My favourite candidate for "the most basic thing that is still unknown" is the momentum carried by light, when it is in a medium (for example, a flash of light in glass or water).
If a block of glass has a refractive index of n, then the light inside that block travels n times slower than the light would in vacuum. But what is the momentum of that light wave in the glass relative to the momentum it would have in vacuum?"
In 1908 Abraham proposed that the light's momentum would be reduced by a factor of n. This makes sense on the surface, n times slower means n times less momentum. This gives a single photon a momentum of ℏω/nc. For ω the angular frequency, c the speed of light and ℏ the reduced Planck constant.
In 1909 Minkowski proposed that actually, the momentum of the same energy worth of light in a material is increased by a factor of n relative to vacuum. This gives a single photon momentum of ℏωn/c.
Which was right? It's still not settled. Not really. A lot of papers will tell you that the "Abraham Minkowski Controversy" is now resolved, but they won't all agree on how it has been resolved. At least three mutually incompatible resolutions have been published. New papers claiming a resolution, or else knocking holes in the old resolutions, are still coming out.
In the rest of this post am going to sketch out why this is a complicated problem, and how some of the proposed solutions work.
An Analogy: The Runner
Why is the momentum of light in glass complicated?
Consider a runner running (as is usual) on land, with some speed c. On their route the runner encounters a region of knee-high water. While travelling through the water our runner travels at a reduced speed of c/n. Now, we ask, what is the momentum of the runner while they are moving through the water?
If we take the mass of everything inside the runner's skin, and multiply it by their velocity then clearly this has fallen by a factor of n relative to their momentum outside the water. However, as the runner wades they will kick a parcel of water along in front of their knees. The total momentum associated with the fact that the runner is in motion is not entirely contained inside their skin.
Suppose that we place an obstacle in the runner's path. They collide with it and come to a complete stop. During the collision we record the impulse on our obstacle and infer the runner's momentum. Clearly, in the process of stopping the runner, we have also stopped the water that they were kicking along with them, so that the momentum such an experiment would detect is not simply c/n, but some higher value, including the water parcel. Indeed, it is not possible to run through water without pushing the water around, so whenever we compare the situation of the runner to the counter-factual where they are standing still, we need to include the momentum of that pushed water. The collision experiment is comparing exactly those states.
What if we posited imaginary "ghost water" that phased through the runner? Then we could avoid thinking about the momentum of the water and keep things simple. Yes, we could. But the ghost water also wouldn't slow the runner down, so that is just the same as the runner on land example.
In the context of the photon in glass we have the momentum in the electric and magnetic fields (like the momentum inside the runner's skin). A photon in glass "plucks" the electron orbitals of the atoms as it passes them by, depositing some amount of energy and momentum into the matter that then springs back out into the electric field a moment later. That momentary retention is the cause of the light slowing down in the first place (or at least, the momentary retention in the time domain Fourier Transforms into the frequency domain as the slow-down).
So, is it just as simple as "The Abraham momentum (/n) describes the electromagnetic field exclusively, while the Minkowski momentum (×n) also includes the part "in the water?"" - That is one position.[1] But alternative theories exist. A similar, competing theory claims claims that Abraham's momentum is the momentum fully in electromagnetic fields, and that some other expression [1/2×(n+1/n) - the direct average of Minkowski and Abraham] gives the total momentum including that in the material response [2].
What is momentum anyway?
I first encountered the Abraham-Minkowski controversy when I was trying to answer a question about recoil. I was considering an idealised thought experiment [3] and to know if it would work I needed to know how recoil worked as light changes medium. When light goes into or out of some piece of glass, which way does the glass get shoved by the recoil, and by how much? This is a basic Newtonian problem, but to answer it one needs to know what to use for the momentum of the light when it is in glass.
Another context in which people worry about momentum is the Heisenberg Uncertainty Principle. You can't know the location and momentum of a photon at the same time, and the more you know one, the less you can know the other.
The Abraham momentum "feels more like" its trying to work with Newton, while Minkowski is Heisenberg's friend. This is basically the short version of the paper by Stephen Barnet[4], where it is argued that the Abraham momentum is the answer to the question "What do I put in Newton's second law to calculate recoil?" and the Minkowski one answers the question "I am doing Heisenberg Uncertainty for a photon in glass, what do I use?"
While I am not convinced by the argument, I think it is getting one thing importantly right, and that is that it asks people to think about what they want to use the number (or vector) they are calculating for. A question of the type "What is X" becomes increasingly difficult to answer as more and more emphasis is put on the "is".
"What is the momentum?"
"What is the momentum?"
"What is the momentum?"
"What *is* the momentum?"
By asking what we want the number for we sidestep that particular rhetorical spiral, and keep ourselves arguing about physics, not definitions. ["Momentum" as a term is arguably over-loaded with too many definitions [5].]
Group Velocity vs Phase Velocity
In a material the phase velocity (how quickly the phase-fronts of the electromagnetic field propagate) and group velocity (how quickly the energy of the field propagates) are not necessarily equal, and these two velocities imply two refractive indices, np and ng which are the slowdown factors of the two relative to vacuum. That same paper from the last section tells you to use ng in Abraham's form (dividing) for kinetic momentum and np in Minkowski's (multiplying) for the momentum that goes with the uncertainty principle.
A Clean-Cut Proof of Abraham's Result
There is a nice, simple, way of motivating that Abraham should be right. Get a glass block, throw a photon at it (from the left). For simplicity assume that the photon transmits through the block without reflection at either edge (this can be achieved using either anti-reflection coatings or post-selecting on a photon that transmits). We will also assume the glass block is rigid, so that it can be moved but doesn't support any vibrational modes (no wobbling like jelly). We also assume the glass block is on a frictionless table so is able to slide either left or right.
As the photon enters the glass block either its momentum falls (Abraham), or increases (Minkwoski). If the photon momentum falls then the glass block starts sliding left to right by momentum conservation. If instead, the momentum increases the glass block starts sliding right to left. In either case, the photon will soon exit the block from the other side and return the block to a standstill. In total the glass will have either shifted slightly left or right depending on which momentum equation is correct.
Usually in physics, for an isolated system, the centre of mass moves at a constant rate. The photon and glass block together constitute an isolated system, and energy-mass equivalence can be used to give the photon a contribution to the centre of mass. The general principle that the centre of mass moved a constant rate can only be satisfied by the glass block moving left to right, and only by it moving by exactly the distance predicted by the Abraham momentum.
Going back to our runner example, the slight shift of the block from left to right can be thought of as the splash as the runner leaves the water.
Putting the water centre of mass slightly to the right. (Although this may be taking the analogy too far). In contrast, Minkowski's momentum would have us believe the glass block gets moved in the opposite direction (towards the light source). So it is not only failing to quantitively satisfy the principle that centre of mass transport should be conserved in an isolated system, but is making a qualitatively opposite prediction, that the glass moves in the opposite direction. Note however, that the principle being broken (uniform motion of centre of mass) is not at all one of the "big principles" of physics, especially not with the extra step of converting the photon energy to mass. I had not previously heard of the principle, and don't think it is anywhere near the weight class of things like momentum conservation.
A variation on this experiment has been done. An optic fibre has a high-power flash of laser light exit from the end facet. As the laser flash leaves the glass (into air) its momentum increases (according to Abraham), which requires a reaction force against the fibre itself, propelling it backwards. So that when the light leaves the fibre springs back (video: https://journals.aps.org/prl/supplemental/10.1103/PhysRevLett.101.243601/Mvi_0025.avi). The spring-back is evidence of the Abraham version of the momentum.
One problem with this experiment is that light (by any definition) has very little momentum, so they had to put fairly high powers through a very small fibre. This means that other things (thermal expansion, static electricity etc) are pushing on the fibre as well, and we need to put some trust in estimates of how strong these competing effects are relative to the direct change in the light momentum. Also, if Minkowski was right the fibre would get tugged down, which (given some elasticity in the fibre) might look somewhat similar to it springing-back.
A Clean-Cut Proof of Minkowski's Result
There is a nice, simple, way of showing that Minkowski's result must be right. Get a mirror, put it in a liquid. Bounce a beam of light off the mirror, and measure the radiation pressure on said mirror as the light bounces off. Repeat for liquids of different refractive indices. Do the experiment, see that the force on the mirror increases with refractive index, as predicted by Minkowski [1]. Simple, and without the measurement uncertainties of the fibre experiment.
No, too simple. While the measurement uncertainties are very low in these experiments, there is a sub-controversy about how they are to be interpreted. Mirrors are characterised not just by the fraction of the optical energy that reflects back from them, but also by the phase-shift imposed on the reflected light wave. For a metal mirror its usually a ≈π phase shift, but any phase shift it possible with the right mirror. The contention is that the phase shift imposed by the mirror will effect the radiation pressure observed, and that all the studies to date saw the Minkowski result only because they all used mirrors with the phase shift π [6]. This paper claims that to get the real momentum you need to average over mirrors with different phase shifts. My own (possibly erroneous) read on this position is that we can imagine the photon is more like a swimmer or rowing boat than a runner, and that momentum is periodically exchanged between the medium and the boat at the optical frequency. The phase on reflection from the mirror (somehow) picks out at which point in the stroke cycle we interrupt and reflect the photon, and that at different points in the cycle different amounts of momentum are in the photon itself or the medium. The claim that one should average over different mirrors leads to the claim that the correct momentum is in fact the direct average of Abraham and Minkowksi.
(Other "pro-Minkwowski" experiments exist. For example by photons being absorbed by atoms in fluid).
Consensus
Consensus is a poor substitute for truth. But if you are interested in the more sociological aspects of science you may well be wondering which theory is "mainstream" and which is the one beloved by cranks and crackpots. My own impression is that engaging with the discussion at all (to advocate any position) is considered slightly cranky. I can't offer evidence for this claim, its all vibes. But it remains my impression. I think its because doing the sort of physics Einstein famously did (looking to replace foundational theories) is perceived partly as a status claim, so when someone comes up with a weird new theory to replace General Relativity it is not enough to label them "wrong" (assuming they are), but the extra label "crank" is appended. Taking any stance on Abraham-Minkowski lands you squarely in the foundational theory work. If I am right about this we have something wrong with our science culture, where people are pushed away from the places of genuine disagreement, which by any reasonable standard are the places most in need of study.
To summarise our options:
My Opinion
For my own position, I want any answer to the problem to offer me the tools needed to answer my original question about weird photon-rockets [3], and any "resolution" that fails to offer an answer to questions of that type isn't really a resolution at all.
At the moment, if I had to pick, I would take either option (3) or possibly (2). The mirrors-in-fluid experiments appear to falsify (1), (3), (5) and (7). [Although the proponents of (3) believe that we need to repeat these experiments with a range of mirrors with different reflection phases.] (4) is unfalsifiable, makes no predictions, and therefore worse than wrong. (6) is slain by the fibre experiment, and fails to engage with the fact that there surely is some distinction between the momentum in the EM field and in the full propagating wave. I have a vague sense that having separate momenta for kinetic and uncertainty related things as in (1) breaks something important somewhere. (Perhaps it allows some scheme to beat Heisenberg uncertainty on a particle's momentum by bouncing a photon in glass of it somehow.)
An important point against theory (2) is that, despite being the most obvious resolution, it was proposed most recently (2017), which strongly implies that the first few times anyone had the idea they thought there was something wrong with it. For example, despite looking like a modified version of (2) proposal (3) actually predates it by 13 years (2004) [2]. It's also unfortunate that the paper advocating most strongly for proposal (2) [1], is, in my opinion, using a model at wildly the wrong level of detail. For a disagreement on a fundamental issue like this you want simple, cartoon models (frictionless, spherical cows in a perfect vacuum). If some contingent detail (the fuzziness of the cows) is changing the answer, then the answer isn't getting to the root of the disagreement. So a minimum of fuzz is good. Mikko Partanen doesn't agree with my philosophy on this and they have a kitchen-sink theory overflowing with, possibly extraneous, detail. Pushing me more towards (3) are two recent (2023) papers that both have supporting evidence for it [9].
Final Thoughts
From the list of options above I have actually left out what appears to be a fairly common position. I have left it out because it is poisonous, and unhealthy. This position goes something like: "This was never a real issue, only mad people think it ever was. Don't worry, we physicists know what we are doing, nothing to see here!" You will not find this in a paper of course, but I see variations of this position in my google searches, and have heard it expressed in person.
There are many reasons this position is poisonous. First, it seems to take a stance against asking questions, and perhaps curiosity itself. Second, it fails to actually provide the answer. Which way do these people think the glass block slides as light propagates through it? Finally, it is simply false. People have disagreed on this issue, and continue to disagree. A disagreement in physics does not mean that we have a tribe of rabid insane "cranks" fighting an enlightened group of intelligent and respectable physicists. One day this issue will be resolved, most likely one of the proposals in front of us at the moment will prove to be the answer, or most of the answer. That will not make the people who studied this problem, on any side, retrospectively insane, bad physicists or unworthy of respect. There is something to see here, a genuine disagreement on something fundamental about how light works, and I think that is exciting, and worthy of curiosity.
"Photon mass drag and the momentum of light in a medium"
Mikko Partanen, Teppo Häyrynen, Jani Oksanen, and Jukka Tulkki
Phys. Rev. A 95, 063850 https://journals.aps.org/pra/abstract/10.1103/PhysRevA.95.063850
"Radiation pressure and the linear momentum of the electromagnetic field".
Masud Mansuripur, Optics Express 5376, (2004) https://opg.optica.org/oe/abstract.cfm?URI=OPEX-12-22-5375 . "Resolution of the Abraham-Minkowski Controversy", Masud Mansuripur, Optics Communications, 283, 1997-2005 (2010). https://wp.optics.arizona.edu/masud/wp-content/uploads/sites/32/2019/04/Resolution-of-Abraham-Minkowski-controversy.pdf
Specifically, some materials have (at some frequencies) a negative index of refraction. In these materials the light's momentum (for some value of momentum) points the opposite direction to that the light propagates. I was interested in whether it was hypothetically possible to use this to build an "Internal Reaction Drive". This would consist of a loop of transparent materials that is half made of negative refractive index materials, and half normal (positive index) materials. As photons travel around the loop in circles their momenta are always in the same direction. To boost my space-ship I fire my laser to inject extra photons into the loop, and the recoil accelerates my ship. The photons are the exhaust particles, but they never leave the ship. When I reach Alpha Centauri I can start harvesting the photons back out of my loop, which will slow the ship down and eventually bring me back to a standstill. To an external observer who couldn't see the inside workings it would look like a reactionless drive. To answer my original question, which was if this Internal Reaction Drive was in principle possible, you would need a definitive answer to the question "What is the momentum of light in matter?" (For use in Newtonian recoil calculations).
This is a sketch of the idea. The photons (yellow kites) go in circles, with propagation direction shown by the kite points. Their momenta (green allows) are in the same direction for most of the loop, so that the total resultant momentum increases as more photons are added. My current weakly held position is that despite appearing mad I think this might in-principle actually work, based mostly off the way momentum conservation of Cherenkov radiation in negative index materials works[10]. Note that, if Minkowski is "just right" then you don't even need negative refractive index materials. You just make the backward part of the loop a higher index material than the forward part. This way the photons have more momentum while going backwards, and also, averaging over time, spend more time travelling backwards that forwards. In contrast, Abraham (with positive index materials) doesn't allow this as the photons spend less time going in the direction in which they have more momentum, so the time average momentum of each as it loops comes to zero. As I find the proposal itself intrinsically somewhat implausible (it is a maximally aggressive violation of the uniform motion of the centre of mass of an isolated system), I think the fact Abraham is somewhat opposed to it working is a weak update in favour of something Abraham-like.
"Resolution of the Abraham-Minkowski Dilemma", Stephen M. Barnett, Phys. Rev. Lett. 104, 070401. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.104.070401
"Radiation Pressure on Submerged Mirrors: Implications for the Momentum of Light in Dielectric Media", Masud Mansuripur. https://opg.optica.org/oe/fulltext.cfm?uri=oe-15-5-2677&id=130623
"Momentum of an electromagnetic wave in dielectric media" Robert N. C. Pfeifer, Timo A. Nieminen, Norman R. Heckenberg, and Halina Rubinsztein-Dunlop. Rev. Mod. Phys. 79, 1197 https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.79.1197
Ad hominem attacks on people 100 years dead on stack exchange! Photons have no electromagnetic charge, but are emotionally charged particles. https://physics.stackexchange.com/questions/3189/is-the-abraham-minkowski-controversy-resolved [Note the author of that answer seems to have got into enough arguments to have a RationalWiki page, which is not a thing I would wish on anybody.]
"Revealing light momentum in dielectric media through standing-wave radiation pressure", Gopal Verma, Vinod Kumar, and Wei Li. Phys. Rev. A 108, 043514 https://journals.aps.org/pra/abstract/10.1103/PhysRevA.108.043514 . Also see "Recoil momentum of an atom absorbing light in a gaseous medium and the Abraham-Minkowski debate", João G. L. Condé and Pablo L. Saldanha. Phys. Rev. A 108, 013511 https://journals.aps.org/pra/abstract/10.1103/PhysRevA.108.013511 who plot a line of best fit in fig.4 that looks like it might be suspiciously close to averaging the Minkowski and Abraham results (about half the gradient of the Minkowski line shown). Weirdly, they don't seem to know about proposal (3), so don't mention the fact they seem to have evidence for it.
"Flipping a photonic shock wave", Shuang Zhang and Xiang Zhang https://physics.aps.org/articles/v2/91#c1