TL;DR: Matryoshka SAEs are a new variant of sparse autoencoders that learn features at multiple levels of abstraction by splitting the dictionary into groups of latents of increasing size. Earlier groups are regularized to reconstruct well without access to later groups, forcing the SAE to learn both high-level concepts and low-level concepts, rather than absorbing them in specific low-level features. Due to this regularization, Matryoshka SAEs reconstruct less well than standard BatchTopK SAEs trained on Gemma-2-2B, but their downstream language model loss is similar. They show dramatically lower rates of feature absorption, feature splits and shared information between latents. They perform better on targeted concept erasure tasks, but show mixed results on k-sparse probing and automated interpretability metrics.
Note: There was also some excellent work on Matryoshka SAEs published by Noa Nabeshima last week. Our work was done independently and in parallel (we even used the same name!). This kind of parallel development provides a nice cross-validation of results - a natural replication in both directions. We believe our work offers complementary qualitative evaluation that further validates and expands upon Noa's findings. There are also some technical differences in our approaches, see the section “Comparison with Noa Nabeshima's MatryoshkaSAE”.
Summary
Matryoshka SAEs are a new variant of sparse autoencoders that train multiple nested SAEs of increasing size simultaneously. The key idea is to train multiple reconstruction objectives in parallel - each sub-SAE must reconstruct the input using only a nested subset of the total latents. The smallest SAE can only use the first few latents, forcing these to capture high-level features, while each larger SAE has access to progressively more latents.
We train them on Gemma-2-2B and evaluate their performance compared to standard BatchTopK SAEs on a range of SAE benchmarks.
Our key positive findings are:
While achieving worse reconstruction loss, Matryoshka SAEs achieve similar downstream cross-entropy loss, suggesting they learn more meaningful features.
- Matryoshka SAEs show dramatically lower rates of feature absorption rates and feature splits when investigating first-letter features compared to BatchTopK SAEs.
- Using Meta-SAEs we show that the latents of Matryoshka SAEs share less information and are more disentangled. This is confirmed by the fact that Matryoshka SAEs perform better on targeted concept erasure tasks.
Our main negative findings are:
- Matryoshka SAEs do not score better on k-sparse probing tasks. However, the results are somewhat confusing and we're not sure how to interpret these results.
- Automated interpretability techniques show only small differences in interpretability. Although the Matryoshka SAE latents in the first few nested sub-SAEs are slightly more interpretable than BatchTopK SAEs, the latents in the later groups are slightly less interpretable.
Together, these results suggest that Matryoshka SAEs represent a promising direction for improving the usability of SAEs, though further experimentation is needed to fully validate their potential.
Code for training our MatryoshkaSAEs can be found at https://github.com/bartbussmann/matryoshka_sae
Feature absorption and composition
Recent work on SAEs has uncovered some concerning issues around how SAEs learn features from LLMs. The core issue is that, while we want SAEs to be a useful interpretability tool, we can’t measure that directly and instead optimize the imperfect proxy of sparsity. In particular, two related problems have emerged: feature absorption and composition.
For example, consider a latent that typically fires on all words starting with the letter E, and a latent that fires on the word "elephant". When the second latent fires (i.e. word “elephant” is the input), both latents fire, which is redundant as elephant implies starts with E, so it could be sparser. Instead, the information (i.e. decoder vector) of "starts-with-E" gets absorbed by a token-specific latent that responds primarily to variations of "Elephant", and the “starts with E” latent gets warped to instead activate on “starts with E except for the world elephant”.
This can occur whenever there is a pair of hierarchical features A and B, where B implies A (i.e. if B is present then A is present but not vice versa).
Similarly, in our meta-SAE work, we found that the decoder vector of a latent representing "Einstein" might also contain the directions for more fundamental features like "scientist", "Germany" and "famous person", instead of these features having dedicated latents, which makes it hard to analyse these high-level features in isolation.
We believe that this is downstream of the sparsity constraint - if two features frequently co-occur then the SAE is incentivised to make a combined latent for when both are present, even if they have no semantic relationship. For example, when representing colored shapes, instead of learning separate latents for "blue" and "square", the SAE might learn a combined "blue square" latent. This allows it to use one active latent instead of two for the same reconstruction.
What are Matryoshka SAEs?
Matryoshka representation learning, as introduced by Kusupati et al., aims to learn nested representations where lower-dimensional features are embedded with higher-dimensional ones, similar to how Russian Matryoshka dolls nest inside each other. The key idea is to explicitly optimize for good representation at multiple scales simultaneously.
We adapt this approach to the context of sparse autoencoders, which means that we can nest multiple sizes of dictionaries in each other. This means that the largest autoencoder uses all latents to reconstruct the input, another autoencoder uses only the first half of the latents, a third uses only the first quarter, etc. etc.
The losses of these nested autoencoders get summed together. This means that the first latents will get used in all losses, whereas the last latent only gets used in a single loss term. This incentivizes the SAE to use the first latents to represent broadly applicable and general features, whereas the later latents can be used for more specific and less frequent features.
In this post, we use the BatchTopK activation function for both our Matryoshka SAE and baseline SAEs. BatchTopK is a variant of the TopK activation function, where rather than keeping the top K activations on each token and setting the rest to zero, in a batch of size B, we keep the top B x K activations across all tokens and set the rest to zero. This enforces an average sparsity of K while allowing the number of latents firing per token to vary. The Matryoshka SAE latent activations and loss are calculated as follows:
Where is the set of nested dictionary sizes. In our experiments, we use a Matryoshka SAE with a maximum dictionary size of 36864, which consists of five nested sub-SAEs. This means that in our case .
During inference, we replace BatchTopK with a batch-independent global threshold, following the methodology detailed in our BatchTopK post. As a result, whether a latent in one sub-SAE fires can depend on latents in other sub-SAEs during training, but during inference the activations of the five sub SAEs can be calculated independently. This leads to an interesting property: once a large MatryoshkaSAE is trained, you can choose to use only a subset of the latents for inference. This flexibility allows you to run a smaller version of the SAE when you have limited compute available, or the smaller SAE contains all relevant latents.
We trained this Matryoshka SAE with an average L0 of 32 on the residual stream activations from layer 8 of Gemma2-2B, using 500M tokens sampled from The Pile.
Code for training our MatryoshkaSAEs can be found at https://github.com/bartbussmann/matryoshka_sae
Comparison with Noa Nabeshima's MatryoshkaSAE
We developed this work in parallel and independently from Noa Nabeshima's work. Therefore it is interesting to compare the two approaches.
- During training, Noa randomly samples the groups of latents from a truncated pareto distribution, whereas we use a fixed group size in line with the original Matryoshka representation learning paper. We suspect that using a fixed group size leads to more stable training and faster convergence. Noa's approach is kind of a continuous version of Matryoshka representations, where each extra latent implies an extra group of latents, which might have the advantage of less hyperparameters and no need to manually (and somewhat arbitrarily) set the group size and number of groups. Furthermore, this may prevent feature absorption to happen within a group of latents.
- We use the BatchTopK activation function, which usually leads to significantly better reconstruction performance than vanilla SAEs.
- We do not reorder the latents during or after training, but instead rely on gradient descent to order the latents in their optimal sub-SAE.
Evaluating the MatryoshkaSAE
Although we only trained a single Matryoshka SAE, each of the nested SAEs was optimized to have a good sparse reconstruction, and can be evaluated individually.
Below we show the reconstruction performance of the different sub-SAEs: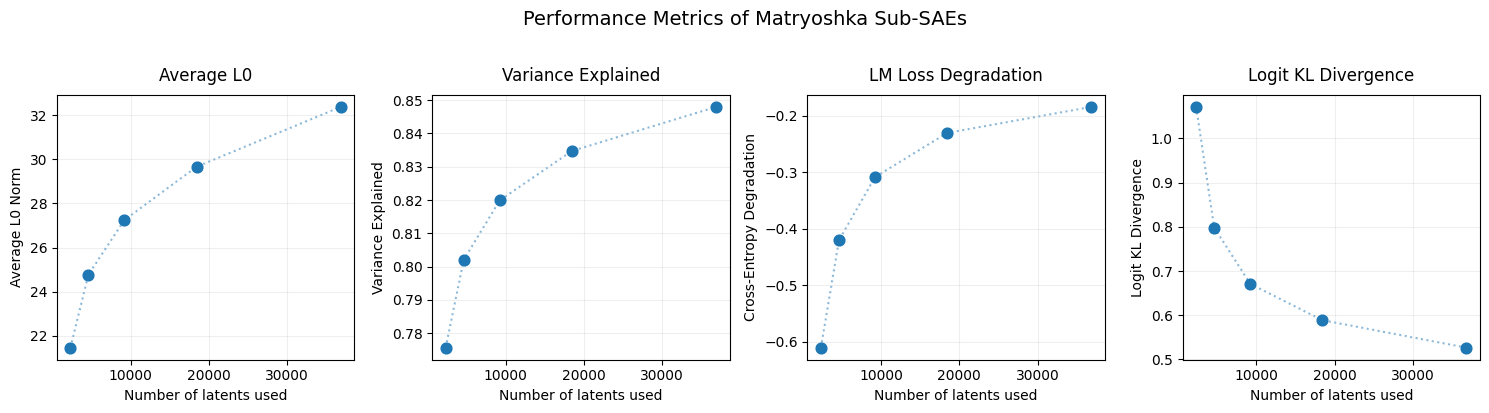
The sub-SAE with only the first 2304 latents uses approximately two-thirds of the active latents! This isn't that surprising given that these are used in five loss-terms, whereas the last 18k latents are only used in one of the loss-terms. Below we show the average frequency of activation of each latent. The five nested groups of latents are clearly visible with different levels of sparsity. Note that unlike Noa Nabeshima, we did not reorder the latents during or after training.
Reconstruction performance
To fairly compare the performance of MatryoshkaSAEs with normal BatchTopK, we train five BatchTopK SAEs with similar dictionary sizes (2304, 4608, 9216, 18432, 36864) and average L0s (22, 25, 27, 29, 32). We evaluate the SAEs on 4096 sequences of length 128 (524288 tokens).
As expected, standard BatchTopK achieves better reconstruction performance (in terms of MSE and variance explained) since feature absorption helps to minimize the number of active latents. However, surprisingly, the MatryoshkaSAE achieves similar downstream cross-entropy loss at the largest dictionary sizes! We find this surprising, our best interpretation is that the Matryoshka SAE learns more meaningful features that better capture the language model's internal representations that are used for the next-token prediction, even though it reconstructs the activations less accurately.
Feature absorption and splitting
To evaluate feature absorption, we use the first-letter task methodology from Chanin et al., as implemented in SAEBench. This approach detects absorption by identifying individual latents that both dominate the feature representation and align strongly with the probe direction. The absorption rate measures what fraction of probe true positives get absorbed into single latents rather than being represented distributionally.
The results reveal a striking contrast between the two architectures: Matryoshka SAEs consistently maintain very low absorption rates (around 0.03) even as dictionary size increases, while BatchTopK SAEs show dramatically increasing absorption with size, reaching rates of approximately 0.29 for the larger models!
We also analyze feature splitting - the tendency for a single conceptual feature to be distributed across multiple latents. Using the same tasks - identifying the first letter of a token - we use k-sparse probing to detect splitting by measuring when additional latents significantly improve classification performance. Here too, the architectures show markedly different behavior: first-letter features remain almost entirely unified in Matryoshka SAEs, while frequently splitting across multiple latents in BatchTopK SAEs.
Feature composition
To analyze the degree of feature composition occurring in our models, we conduct an experiment using meta-SAEs trained on the decoder matrices of both architectures. For each (sub-)SAE, we train a meta-SAE with a dictionary size one-quarter that of its input SAE and an average of only 4 active meta-latents. By measuring how well these meta-SAEs can reconstruct the original decoder matrices, we gain insight into the compositional nature of the learned features. The key intuition is that if a smaller meta-SAE can explain a large portion of variance in the decoder directions, it suggests the original features are being composed from a more compact set of basic building blocks, corresponding to high-level features that got absorbed into latents for lower level features.
The results reveal a clear difference between the architectures: meta-SAEs explain substantially more variance in BatchTopK SAE decoder directions compared to Matryoshka SAE directions. This suggests that Matryoshka SAE latents are more disentangled, with less shared information between them. This aligns with our architectural intuition - the nested structure of Matryoshka SAEs forces smaller sub-SAEs to learn broad, general features, while BatchTopK SAEs tend to fragment these general features and share them across multiple specialized latents through splitting and absorption.
Sparse probing
We also evaluate the capability of the SAEs to be used as concept probes. We use three different metrics. The first method, k-sparse probing, examines representation quality through classification tasks. This approach selects the k most informative latents and tests how well they encode features through simple linear probes on a range of tasks. The second method, Targeted Probe Perturbation (TPP), measures how well an SAE can isolate individual concepts without affecting others. The third method, Spurious Correlation Removal (SCR), measures how effectively an SAE separates correlated features by identifying and ablating spurious correlations in biased datasets. For more information about these metrics, see SAEBench.
Looking at the results, we see that the k-sparse probing results are mixed. We would have expected the Matryoshka SAE performance to increase monotonically with dictionary size, as the smaller SAEs are subsets of the larger SAEs. Given that this is not the case, we suspect that the feature selection is not optimal and we are not sure how to interpret the results.
The TPP results paint a clearer picture. Matryoshka SAEs consistently outperform BatchTopK SAEs across nearly all dictionary sizes and number of ablated latents, demonstrating superior concept isolation capabilities. This indicates that Matryoshka SAEs learn more disentangled representations where individual concepts can be targeted more precisely.
For SCR, we observe that Matryoshka SAEs become increasingly effective at removing unwanted correlations as dictionary size grows. In contrast, BatchTopK SAEs maintain relatively consistent SCR performance regardless of dictionary size.
Taken together, these results are a bit ambiguous but suggest that Matryoshka SAEs tend to learn more modular, disentangled features compared to BatchTopK SAEs. The hierarchical training appears to encourage cleaner separation between concepts, resulting in less information shared between different latent dimensions.
Interpretability
Finally, we look at the interpretability of the latents. For this, we use the automated interpretability implementation in SAEBench. The automated interpretability evaluation quantifies SAE feature interpretability using gpt4o-mini as an LLM judge through a two-phase process. First, in the generation phase, the system collects SAE activations from webtext sequences, selecting high-activation examples and sampling additional weighted sequences. These are formatted with highlighted tokens and used to prompt an LLM to generate feature explanations. In the scoring phase, a test set combining top activations, weighted samples, and random sequences is presented to an LLM judge along with the feature explanations. The judge predicts which sequences would activate each feature, with the prediction accuracy determining the final interpretability score. This approach builds on established methodologies from Bills et al. and EleutherAI.
Looking at the interpretability scores, we see an interesting pattern emerge. The early nested sub-SAEs actually perform slightly better than their BatchTopK counterparts in terms of interpretability. However, this advantage doesn't hold for the later groups of latents, which show somewhat lower interpretability scores. These differences are relatively subtle and may just be noise - all models achieve scores between 0.84 and 0.88 - but they hint at an interesting hypothesis: perhaps the later latents, which need to coordinate with the smaller nested sub-SAEs to represent features, are learning latents that are harder for automated interpretability techniques to understand.
Conclusion and future work
Our evaluation of Matryoshka SAEs reveals an interesting trade-off. While they achieve lower reconstruction performance than BatchTopK SAEs, they demonstrate several key advantages: dramatically reduced feature absorption and composition, and cleaner separation between concepts. Intuitively, Matryoshka SAEs are regularized to stop them properly exploiting phenomena like feature absorption to maximize sparsity, which should harm performance. The fact that MSE is damaged much more than cross-entropy loss, where the change is ambiguous, suggests that the performance hit may be small, as cross-entropy loss seems closer to what we care about.Their nested structure also provides practical flexibility, allowing compute/performance trade-offs during inference. These results suggest that Matryoshka SAEs are a promising direction.
Perhaps most importantly, Matryoshka SAEs seem to better align with our intuitive goals for interpretable representations - having general features built upon by more specific ones in a progressive sequence. This natural ordering of features from general to specific could be helpful as we scale up interpretability research.
Several directions warrant further investigation:
- Qualitative investigation: Investigate case studies of feature absorption, splitting or composition in normal SAEs and compare them to Matryoshka SAEs - have they changed as anticipated? Do Matryoshka SAEs learn concepts systematically not learnt in SAEs of a similar size, and vice versa?
- Architectural tweaks: What is the effect of latent sorting that Noa uses on the benchmarks? What about the random selection of group sizes vs fixed group sizes? Should the smallest sub-SAE get gradients from all losses, or should the losses from larger sub-SAEs be stopped? Should we set an individual average TopK for each sub-SAE or does the global approach as used in this post make more sense?
- Further investigation of Sparse Probing: How is it possible that adding more latents to the sparse probing task actually hurts performance? Is it overfitting and not selecting the optimal latents?
- Human interpretability: Is the effect of less interpretable latents in the later groups of the Matryoshka SAE due to automated interpretability techniques, or do these replicate when using human judges?
- Hyperparameter investigations: What is the best number of nested sub-SAEs? What are their sizes?
While there's more work ahead, we believe that Matryoshka SAEs represent a meaningful step toward better monosemantic representations.
Acknowledgements
Thanks to Matthew Wearden for providing research management support and feedback during this project. Thanks to Tom White (@dribnet) for first planting the seed of applying Matryoshka representations to SAEs. We would also like to thank Adam Karvonen for excellent discussions about Matryoshka SAEs and his help with running the SAEBench evaluations. Thanks to Callum McDougall for making the feature absorption explainer and giving permission to use it in this post.
This work is done in the extension phase of MATS 6.0 under the mentorship of Neel Nanda. Bart and Patrick are grateful for the funding of AI Safety Support, which made our MATS extension program and this research possible.
Contribution Statement
Bart Bussmann implemented the architecture, conducted the experimental work, and wrote the initial draft of this post. Patrick Leask participated in early conceptual discussions about the Matryoshka SAE approach and provided input during shared project meetings. Neel Nanda provided mentorship throughout the project, contributing to implementation and experimental design decisions, and helped with editing and framing the blog post.