This post will be about the main points of evidence for the existence of dark matter. To evaluate whether a competing theory to dark matter is plausible, it's important to know what the actual arguments in favor of dark matter are in more detail than just "dark matter is the stuff you have to add to get galactic rotation curves to work out". A competitor has to address the strongest arguments in favor of the existence of dark matter, not just the weaker fare like galactic rotation curves.
So, when reading some hot new arxiv paper about dark matter or the lack thereof, it is fairly useful to know the top five lines of evidential support for dark matter (in my own personal estimation, others may differ). This lets you at least check whether the result is directly addressing the major cruxes that the case for dark matter rests upon, or just picking off one particular piece of evidence and sweeping the rest under the rug, even if you lack the full technical ability to evaluate the claimed result.
This post will be saving the best for last, so if you're not going to read the whole thing, skip down to sections 4 and 5.
Also, what exactly is meant when the term "dark matter" is used in this post? Anything with mass (so it's affected by gravity and gravitationally influences other things) which does not interact via the electromagnetic force. Electrons, protons, nuclei, and atoms emphatically do not count. Black holes, neutrinos, WIMPS (weakly interacting massive particles), and axions would count under this definition. The last two are theoretical, the first two are very much established. Of course, it would be a massive cop-out to go "neutrinos exist, therefore dark matter does", so "dark matter" will be used with a followup connotation of "and whatever the heck is (we don't know yet), there must be 5x more of it in the universe than matter made of atoms or atom parts, no way around that whatsoever"
Point 1: Galactic Rotation Curves
The story begins with galaxy rotation curves, which were the original motivation for postulating dark matter in the first place. Given a point gravitational mass, it's pretty simple to calculate the velocity of something orbiting around it, depending only on how far away the object is orbiting and how much mass is in the central point. Stuff orbiting further out from a point mass will be orbiting at a lower velocity.
With a bit more work, given a disc of mass, you can calculate the velocity of something orbiting around or within it. For this, the graph of orbital velocity vs distance from the center of the disc first rises, then falls. Orbital velocities are low in the center because stuff orbiting near the center of the disc isn't orbiting around very much mass, and orbital velocities are low at the outside of the disc, because you get closer to being able to approximate things by the situation "your distant object is orbiting around a central point mass", which, as previously discussed, already exhibits the "stars on further-out orbits move more slowly" behavior.
Computing this in practice requires knowledge of two things, however. First, you need to know how fast the stars in the galaxy are orbiting around the center. Second, you need to know the radial distribution of mass in the disc or ellipse.
It's pretty easy to tell how fast stars in a galaxy are orbiting around the center, for suitably chosen galaxies. Stars have emission and absorption lines at very specific frequencies measured to very high accuracy, which only depend on details of atomic physics that don't change in different galaxies. So, as an example, you could pick an edge-on spiral galaxy, and look at the position of the absorption lines in the center of the galaxy. Then, you can look at the two edges of the galaxy, and in one edge, the emission/absorption line will be shifted to higher frequencies (the side of the galaxy that is rotating towards you), and in the other edge which is rotating away from you, the line will be shifted to lower frequencies, and with this you can accurately measure the rotational velocity of stars around the center of the galaxy.
But what about figuring out the radial distribution of mass? Well, for stars, by looking at a bunch of binary stars in the Milky Way, and stellar evolution models, we have an accurate idea how the color of a star corresponds to its mass and luminosity, so if you know how far away a galaxy is, and it has a spectrum corresponding to a bunch of orange K-type stars, you can use how bright the galaxy is, how far away it is, and the luminosity-to-mass relationship for K-type stars to figure out about how much stellar mass is there. It's more complicated than that because there's many different types of stars, but it can be done.
Of course, stars aren't all the mass we know of. In fact, they often make up a rather small portion of the visible mass in a galaxy. There are also clouds of hot ionized hydrogen, which emit high-frequency light, UV and up. And clouds of monoatomic hydrogen can be picked out in the radio spectrum from their characteristic 21-cm radio waves. Similarly, clouds of diatomic hydrogen, , have their own characteristic spectral lines. Just check the luminosity of those vs the distance of the galaxy, and you can figure out about how much gas of the various types there is.
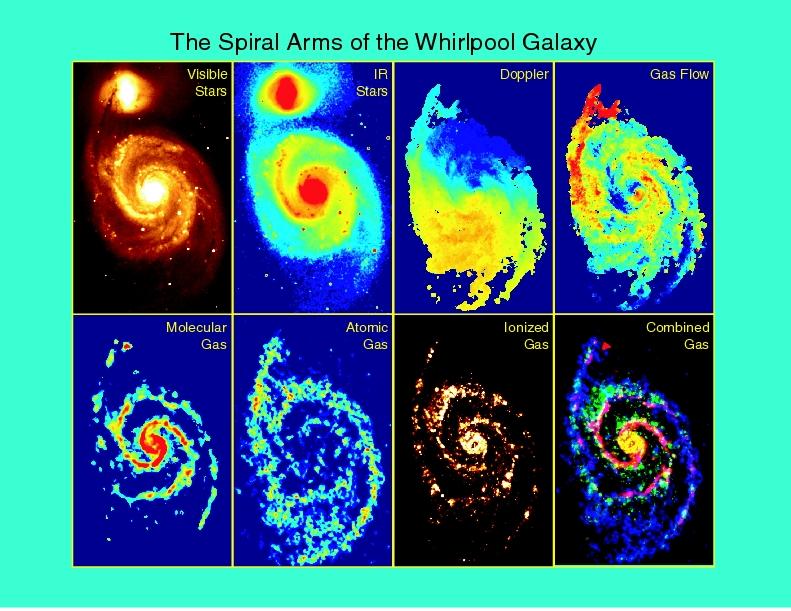
Of course, this might not account for all the mass in a galaxy, there might be some stuff that was missed. But we can try adding up all the mass that we see and where we see it, and check that against the orbital velocity of the stars to see if we found everything or missed some stuff.
And, lo and behold, if you check the speed at which stars orbit in galaxies, it does not exhibit the expected behavior. Yes, orbital velocities are low in the center, but towards the outskirts, where you'd expect most of the mass to be more towards the middle of the galaxy so the stars should be slowing down in their orbits, they're either orbiting just as fast or even speeding up slightly. We can check even further out by looking at the 21 cm line of cold monoatomic hydrogen, and it's still rotating fast. Which would all be accounted for by the galaxy being embedded in a big cloud of mass.

On its own, this isn't terribly convincing. The estimates of the rotation curves rely on us managing to account for all the matter we saw. So maybe there are just big clouds of hydrogen that we haven't managed to find yet. Yes, there's a bunch of missing mass, but jumping from that to concluding that it isn't made of atoms is quite a stretch. Or maybe a full GR (General Relativity) treatment of the galaxy would account for things? Or maybe this is pointing towards a change in the laws of gravity itself on large scales? More on these options later.
For now, I'll observe something quite interesting. While most galaxies have rotation curves like this which indicate that there's about 6x more mass there than can be seen (on average), this number certainly isn't uniform across the universe. It's a good average for galaxy clusters, but the ratio experiences a lot more variation as the galaxy gets smaller, with the most extreme cases being found in dwarf galaxies. There are some dwarf galaxies where the visible matter pretty much accounts for the galactic rotation curve, and some dwarf galaxies where the rotation curves seem to indicate that there's >100x more matter there than was observed. So, whatever explanation you invoke to account for galactic rotation curves, it should hopefully account for the existence of the occasional dwarf galaxy where what you see is what you get.
I count this as one of the weaker pieces of evidence in favor of dark matter, partially because it was the piece of evidence that lead to dark matter being postulated in the first place. It does no good to go "look at how dark matter perfectly accounts for galactic rotation curves" when this evidence was what lead to dark matter being promoted to a live hypothesis in the first place.
The other reason why it's one of the weaker pieces of evidence is that dark matter isn't a perfect fit, just a pretty good one. Pretty much every competitor theory to dark matter starts out with trying to replicate the galactic rotation curves, and so they also do a fairly good job at it.
Simulations of galactic evolution are quite hard, and the existence of an extended dark matter halo does account for the rotation curves quite well (as it was supposed to do), but there's two predictions from these simulations which reality doesn't quite seem to bear out.
The first is the cuspy halo problem. The simulations seem to indicate that there should be a considerable overabundance of dark matter in the core of a galaxy, where empirically it looks more like a uniform distribution given how the stars are moving in there. The best explanation I've seen is this paper which indicates it's a computational artifact of the algorithms used in the simulations to get a massive N-body physics problem down from interactions per timestep to computations per timestep, though I lack the technical expertise necessary to fully evaluate said paper.
The second is the dwarf galaxy problem. The simulations seem to indicate that there should be about 50x more dwarf galaxies around a galaxy than actually seem to exist. From searching harder, we have found more ultra-dim dwarf galaxies around the Milky Way than were thought to exist at the time, and these new ones seem to have very high ratios of dark matter in them by how the stars are moving. So, one of the proposed explanations is that maybe there are in fact a whole bunch of dwarf-galaxy-sized lumps of dark matter around our galaxy that have so little gas and stars associated with them that we don't know they're there.
A second possible explanation to the dwarf galaxy problem is warm dark matter. Roughly, if we assume dark matter is made up of a bunch of particles, we've got three possibilities. The first is that they're going near light-speed, as neutrinos do. This is hot dark matter. Or they could be traveling at fairly low velocities, like <10 percent of lightspeed. This is cold dark matter. Or they could be something in the middle, ie, warm dark matter. If all your particles are going super-fast and only interact via gravitation, they would form an enormous spread-out fluffy mass, while if all your particles aren't going fast at all, gravitation can draw them into much smaller, clumpier, and denser structures.
Hot dark matter is ruled out (well, technically, neutrinos are a form of hot dark matter, but they don't account for anywhere near the 5x mass excess), as the size of its clumps would be considerably larger than a galaxy, and simulations of galaxy formation with the dark matter being hot don't produce anything like what we see today. So that rules out neutrinos as a possibility, because if they made up most of the dark matter, you wouldn't get galaxies looking like they currently do.
Cold dark matter, being much more clumpy, produces that profusion of dwarf galaxies which may or may not exist. So, if the dark matter is warm, it would smooth things out enough to still correctly account for what occurs at the scale of a big galaxy, but not a tiny little dwarf galaxy, as the stuff is moving too fast to form structures of that small size. From talking to someone in the field, apparently cold dark matter is favored, though I'm not entirely sure why. It has a lot more particle candidates from theoretical physics than warm dark matter does, but there's probably some other reason I missed.
So, for dark matter vs competitors, galactic rotation curves don't settle it, as all the competitors for dark matter try to explain those rotation curves as well. There's also some unsolved issues where dark matter accounts for galactic rotation curves, but the simulations don't quite match up with what we see, what with their cuspy halos and profusion of dwarf galaxies. But then we get into meatier fare.
Point 2: Large-scale Universe Structure
We can run simulations of what the large-scale structure of the universe would look like, starting from the conditions a few thousand years after the Big Bang. Just throw in different amounts of regular matter (hydrogen-helium gas mix), light, dark energy, and matter which doesn't interact with electromagnetism, introduce some overdensities and underdensities of the magnitude and spacing we see in the Cosmic Microwave Background, and run it with General Relativity (this is more tractable than giving galactic formation the full GR treatment). Then just compare against the observed large-scale structure of the universe, to rule out combinations of these components. We should get a match with the pattern of voids and filaments and their densities and spacing we observe in the universe.
Well, first, how do we know the large-scale structure of the universe? Lots of large-scale automated deep-sky surveys, with redshift as a fairly accurate distance proxy, calibrated against type Ia supernova.
There's also another neat trick with hydrogen gas. If you have some super-bright source of high-energy radiation, like a quasar (the brightest things in the universe), and the light passes through a cloud of neutral hydrogen gas, the hydrogen gas will absorb a particular frequency of UV light. Also, the expansion of the universe doesn't just redshift light because the galaxy is traveling away from us, it also redshifts light because the light literally stretches out due to the expansion of space over the course of its journey across the universe.
So, if you've got a quasar, and the light passes through a cloud of hydrogen gas, that particular UV frequency of light will get absorbed, making a spectral line. Then, if the light keeps going and redshifting and runs into another cloud of hydrogen gas in its travels, the old UV spectral line will have been redshifted down, and light which used to be above that particular spectral line will get redshifted to line up with that frequency of light. So now, looking at the quasar spectrum, there are two absorption lines, the lower one for when the light first went through a cloud of hydrogen, and the higher one for when the light more recently went through a hydrogen cloud. Although, usually, there's a lot more than two lines. By looking at how deep the absorption lines are in the spectrum, and where they are, you can build up a picture of how much cold hydrogen gas is at what distances along the line-of-sight between us and the quasar.

So, how do the simulations do at reproducing what we see in the universe around us? Well, first-up, this is an opportunity to falsify the usual picture of dark matter. If a 5-to-1 ratio of dark matter to hydrogen/helium gas doesn't replicate the large-scale structure of the universe, the theory dies right here.
Since I'm citing this as a piece of evidence, it obviously must have passed. In fact, this was known as a problem early on, that for the standard accounting of known mass in the universe, it wasn't enough to permit large clusters and walls of galaxies to form. The ordinary matter would be too spread out and you'd just get little clumps of galaxies instead of the larger superclusters and walls. That was another reason dark matter was an attractive hypothesis, because if there's a lot more mass in the universe, you could get enough mass for large-scale structure formation. The dark matter would gravitate into clumps, which would provide a big gravitational well for the ordinary matter to accrete at the bottom of and form galaxies. At the time, this wasn't super-detailed, the more detailed computer simulations and large-scale surveys of the cosmos (which, again, could have falsified dark matter being in 5x abundance) came afterwards.
This is not accounted for by just gravitoelectromagnetic effects. Modified gravity theories also have a hard time explaining this one. It still leaves open the possibility that maybe there's just a whole boatload of extra hydrogen and helium out there that we just haven't spotted yet for whatever reason.
So that's the second line of evidence, large-scale simulations of the universe most accurately replicate its structure with about 6x more matter than is currently accounted for.
Point 3: Galactic Cluster Lensing
And now we get into the third thing, to further drive the nail into gravity-based competitors.
One of Einstein's famous original predictions was of the magnitude of displacement of the image of a star from its usual position during a solar eclipse, due to gravitational lensing from the sun. GR passed with flying colors. So, another concievable test that you can carry out for dark matter (once you gain a Hubble Telescope to play around with) is to find a bunch of galaxy clusters which are big enough to have gravitational lensing effects, and see how much of a dent they make in the images of the background galaxies. If it indicates that there's 6x more matter than you see, then that's another test passed.
Much of the visible mass in a galactic cluster is in the form of hot plasma which emits X-rays and UV light, from the galaxies moving around and running into each other at high speed which heats up their surrounding gas. This can be weighed by checking the plasma luminosity, and using the spectra to infer temperature of the gas and how brightly it should be glowing, and then if you know far away the galactic cluster is, you can solve for the amount of plasma present.
A bunch of studies on this are carried out using weak lensing, which looks at subtle distortions of the background galaxies, but there are galactic clusters with far more spectacular instances of gravitational lensing, as pictured below.

And, what do you know, the gravitational lensing of galaxy clusters all indicate a mass about 6x more than the hot gas and stars and every other detectable source of mass would indicate. Again, this is another thing that modified gravity theories really struggle to deal with. They ace the galactic rotation curves, but don't do so well with galaxy cluster dynamics.
Point 4: The Bullet Cluster
And while we're on the topic of galaxy clusters, there's also the Bullet Cluster. Which wasn't exactly an advance prediction, but it's another thing that's really hard for competitors to explain, while the standard picture of dark matter makes perfect sense of it.
Pretty much, the Bullet cluster is a pair of galaxy clusters that rammed into each other. Stars are very widely spaced. If the Milky Way and Andromeda collided, there would only be about one stellar collision in the whole interaction, IIRC. So the stars should mostly just go through each other. If dark matter mostly doesn't interact with itself, the dark matter blobs should just go through each other. The same cannot be said for the hot ionized plasma which makes up much of the mass in a galactic cluster, however. The particles in it are charged, and would, with high probability, get slowed down and heated up from ramming into a galactic-cluster-sized blob of hot plasma heading the other way.
And so, we can view the cluster in X-rays to see where most of the visible mass, including stars, is. And we can check the subtle gravitational lensing of background galaxies to see where the actual mass is. And now... check out the following image. Pink is the X-ray emitting gas, purple is where the mass is according to background gravitational lensing.

Explain this with modified gravity.
This also weighs against the "maybe it's just a bunch of ordinary hydrogen and helium in some gas form we can't see" hypothesis, because it's rather hard to shoot two galaxy-cluster-sized blobs of gas of each other and have them pass straight through each other.
Point 5: The CMB Power Spectrum
And now we come to my personal favorite piece of evidence. The Bullet cluster is usually taken as the most spectacular line of evidence for dark matter, but the CMB power spectrum is what lets us conclusively rule out that dark matter is anything born of atoms.
This was very much an advance prediction. The detailed measurements of the pattern of ripples in the cosmic microwave background (CMB) radiation, in enough detail to get the following graph, were not around at the time dark matter was postulated. It came in around 2000 and later, mostly from the WMAP probe, and was then refined by the Planck probe.

Roughly, this graph is telling you the magnitude of the fluctuations on different scales of the cosmic microwave background. On the far left of this graph, it's plotting the amplitude of CMB variations over larger regions of space, where the cosmic microwave background looks pretty uniform. On the far right of this graph, it's plotting the amplitude of CMB variations on the smallest scales. It says that most of the fluctuations in the CMB are accounted for on the scale of about 1 degree. This spectrum encodes information about what was going in the early universe, the characteristic length scale on which the universe had ripples during its formation.

The positioning of the first peak tells you about the curvature of the universe. It's the dominant length scale on which the universe has clumps or voids. This can be measured now, from large-scale universe structure. If the first peak was shifted to the left or right, it would correspond to the major fluctuation scale of the universe looking bigger/smaller at early times than it does now, which is characteristic of large-scale universe curvature. The universe, as near as we can tell, looks flat (ie, like , euclidean 3-space) on large scales. The curvature of the universe depends on what it has in it. A universe with a whole bunch of matter/energy in it would be positively curved. The energy in empty space which would account for the cosmological constant (whatever the hell it comes from), accounts for 69% (plus or minus 0.6%) of the total mass-energy budget you need for a flat universe. And, you guessed it, for the remaining known mass, you don't get anywhere near the 31% necessary.
But this isn't the only way that you can check up on dark matter with the CMB power spectrum! In the early universe, everything was hot and dense and there was a lot of radiation/light around. So, matter which interacts with radiation would heat up and expand back again if it started compressing, while matter which doesn't interact with light but does interact with gravity wouldn't have that effect. Having different amounts of ordinary atomic matter vs dark matter early on in the universe produces different characteristic patterns in the spectrum, with ordinary atomic matter tending to enhance the even-numbered peaks, and dark matter tending to enhance the odd-numbered ones.
And, lo and behold, the CMB power spectrum (particularly the second and third peaks) perfectly fits with ~5% of the universe's mass-energy being accounted for by matter, and ~26% of the universe's mass-energy being accounted for by dark matter, summing up to 31%.
This is how we know dark matter can't be anything made of atoms. Early on in the universe, it was more of a very hot homogenous soup, so everything made of atoms in the current day was in the form of a hot dense soup of gas way back when. So this is directly measuring the proportion of "matter made of atoms" to "??? stuff that has gravity but doesn't interact with light". And it fits!
From an advance-prediction standpoint, we get something else interesting. The CMB ripples seemed to indicate that there was more baryonic (hydrogen and helium) matter in the universe that had previously been accounted for around galaxies, which was promptly dubbed the "Missing Baryon problem". It was a bit tricky to account for, because much of it was in the form of incredibly wispy warm hydrogen in great streamers between the galactic clusters and in the voids, but by 2020, the last missing 30% of the CMB-indicated hydrogen and helium was accounted for and the missing baryon problem was solved.
Conclusion:
So, the five main lines of support for dark matter are: galactic rotation curves, accurately replicating the large-scale structure of the universe in simulations, the extra mass still being present when you look at galaxy cluster lensing, the bullet cluster having the mass and the visible gas in different locations, and finally, perfectly accounting for the pattern of ripples in the cosmic microwave background in two different ways.
So, this should hopefully provide some background on why dark matter is widely accepted to be a Thing, and furnish some useful heuristics on reading a paper on competitors to dark matter for explaining things. If they only talk about galactic rotation curves and don't try to explain the CMB spectrum and Bullet Cluster, you can safely throw the paper in the trash, as these are the two major hurdles that the dark matter competitors fail to clear. Conversely, if there's a paper proposing an alternative to dark matter that manages to explain the CMB power spectrum and the Bullet Cluster, it's now safe to take it more seriously. It's the astrophysics equivalent of Scott Aaronson's heuristics on whether a P vs NP proof is worth taking seriously.
But what even is dark matter, anyways? Well... there are a lot of possibilities, and it would be premature to conclude that it's any particular one of them, or even that we won't get hit with something out of left field. The basic constraints we know are: It's affected by gravity and has gravity. It doesn't interact through electromagnetism, otherwise it wouldn't be consistent with the CMB spectra. If it does interact through the weak or strong force, the interaction will be really weak, because we've built a bunch of big particle detectors to check for dark matter with appreciable weak or strong force interactions and haven't come up with shit. Dark matter shouldn't be hot/travel at a sizeable chunk of the speed of light, because otherwise the large-scale structure of the universe would be too uniform and galaxies wouldn't have the structure they do, which rules out neutrinos. And you should be able to fire two big lumps of it at each other and have them pass straight through each other, because the Bullet Cluster is a thing.
Hopefully this post was informative.
Thank you. The multipole moment chart is cited frequently and I was always wondering what it would look like in counterfactual worlds without DM. Therefore I am especially grateful for your explanations:
Can you provide a link to read up further on this? Preferably not a summary but the actual research article.