It's been a couple months, but I finally worked through this post carefully enough to respond to it.
I tentatively think that the arguments about trammelling define/extend trammelling in the wrong way, such that the arguments in the trammelling section prove a thing which is not useful.
The Core Problem
I think this quote captures the issue best:
The agent selects plans, not merely prospects, so no trammelling can occur that was not already baked into the initial choice of plans. The general observation is that, if many different plans are acceptable at the outset, DSM will permit the agent to follow through on any one of these; the ex-post behaviour will “look like” it strictly prefers one option, but this gets close to conflating what options are mandatory versus actually chosen. Ex-post behavioural trajectories do not uniquely determine the ex-ante permissibility of plans.
For purposes of e.g. the shutdown problem, or corrigibility more generally, I don't think I care about the difference between "mandatory" vs "actually chosen"?
The rough mental model I have of DSM is: at time zero, the agent somehow picks between a bunch of different candidate plans (all of which are "permissible", whatever that means), and from then on it will behave-as-though it has complete preferences consistent with that plan.
What the quoted section seems to say is: well, since we don't know before time zero which of the candidate complete preferences will be chosen, it's not trammelling.
That seems like the wrong move.
One angle: how does that move translate back to the usual setting of trammelling (i.e. "prospects" rather than plans)? Seems like the corresponding move would be to say "well, the agent's preferences will move toward completeness over time, but we don't know ahead-of-time which complete preferences they'll move toward, therefore it's not trammelling". And that argument pretty clearly seems to redefine trammelling as a different thing than what it usually means, and then just ignores the thing usually called the trammelling problem.
If we use the term "trammelling" more like its usual use (as I understand it based on my barely-extant exposure), then it sounds like the proposal in the post just frontloads all the trammelling - i.e. it happens immediately at timestep zero.
Application to Shutdown/Corrigibility
Another angle: suppose I'm working on the shutdown problem. As of now, I don't know how to solve that problem even given a way to stabilize incomplete preferences, so I may just be missing something. That said, I can kinda vaguely pattern-match the setup in this post to the problem: I want to have one "permissible" choice which involves the shutdown button not being pressed, and another "permissible" choice which involves the button being pressed, and I want these two choices to be incomparable to the agent. Now (my mental model of) the DSM rule says: when the agent is turned on, it somehow chooses between (two plans leading to) those two options, and from then on out acts as though it has complete preferences consistent with the choice - i.e. it either (follows a plan which) makes sure the button is pressed, or (follows a plan which) makes sure the button is not pressed, and actively prevents operators from changing it. Which sounds like not-at-all what I wanted for the shutdown problem!
So, it seems like for applications to corrigibility, ex-post behavioral trajectories are the thing I care about, not ex-ante "permissibility" of plans. Though again, I don't actually know how to use incomplete preferences to solve shutdown/corrigibility, so maybe I'm just not thinking about it right.
This is a tricky topic to think about because it's not obvious how trammelling could be a worry for Thornley's Incomplete Preference Proposal. I think the most important thing to clarify is why care about ex-ante permissibility. I'll try to describe that first (this should help with my responses to downstream concerns).
Big picture
Getting terminology out of the way: words like "permissibility" and "mandatory" are shorthand for rankings of prospects. A prospect is permissible iff it's in a choice set, e.g. by satisfying DSM. It's mandatory iff it's the sole element of a choice set.
To see why ex-ante permissibility matters, note that it's essentially a test to see which prospects the agent is either indifferent between or has a preferential gap between (and are not ranked below anything else). When you can improve a permissible prospect along some dimension and yet retain the same set of permissible prospects, for example, you necessarily have a preferential gap between those remaining prospects. In short, ex-ante permissibility tells you which prospects the agent doesn't mind picking between.
The part of the Incomplete Preference Proposal that carries much of the weight is the Timestep Near-Dominance (TND) principle for choice under uncertainty. One thing it does, roughly, is require that the agent does not mind shifting probability mass between trajectories in which the shutdown time differs. And this is where incompleteness comes in. You need preferential gaps between trajectories that differ in shutdown time for this to hold in general. If the agent had complete preferences over trajectories, it would have strict preferences between at least some trajectories that differ in shutdown time, giving it reason to shift probability mass by manipulating the button.
Why TND helps get you shutdownability is described in Thornley's proposal, so I'll refer to his description and take that as a given here. So, roughly, we're using TND to get shutdownability, and we're using incompleteness to get TND. The reason incompleteness helps is that we want to maintain indifference to shifting probability mass between certain trajectories. And that is why we care about ex-ante permissibility. We need the agent, when contemplating manipulating the button, not to want to shift probability mass in that direction. That'll help give us TND. The rest of Thornley's proposal includes further conditions on the agent such that it will in fact, ex-post, not manipulate the button. But the reason for the focus on ex-ante permissibility here is TND.
Miscellany
For purposes of e.g. the shutdown problem, or corrigibility more generally, I don't think I care about the difference between "mandatory" vs "actually chosen"?
The description above should help clear up why we care about multiple options being permissible and none mandatory: to help satisfy TND. What's "actually chosen" in my framework doesn't neatly connect to the Thornley proposal since he adds extra scaffolding to the agent to determine how it should act. But that's a separate issue.
The rough mental model I have of DSM is: at time zero, the agent somehow picks between a bunch of different candidate plans (all of which are "permissible", whatever that means), and from then on it will behave-as-though it has complete preferences consistent with that plan.
...
it sounds like the proposal in the post just frontloads all the trammelling - i.e. it happens immediately at timestep zero.
The notion of trammelling I'm using refers to the set of permissible options shrinking as a result of repeated choice. And I argued that there's no trammelling under certainty or uncertainty, and that trammelling under unawareness is bounded. Here's why I don't think you can see it as the agent behaving as if its preferences were complete.
Consider the case of static choice. It's meaningful to say that an agent has incomplete preferences. (I don't think you disagree with that but just for the sake of completeness, I'll give an example.) Suppose the agent has preferential gaps between all different-letter prospects. From {A,A+,B} the agent will pick either A+ or B. Suppose it picks B. That doesn't imply, say, that the agent can be thought of as having a strict preference for B over A+. After all, if you offered it {A,A+,B} once again, it might just pick A+, a contradiction. And you can set up something similar with transitivity to get a contradiction from inferring indifference between A+ and B.
Onto dynamic choice. As you write, it's reasonable to think of various dynamic choice principles as immediately, statically, choosing a trajectory at timestep zero. Suppose we do that. Then by the argument just above, it's still not appropriate to model the agent as having complete preferences at the time of choosing. We're not frontloading any trammelling; the set of ex-ante permissible prospects hasn't changed. And that's what we care about for TND.
I can kinda vaguely pattern-match the setup in this post to the problem: I want to have one "permissible" choice which involves the shutdown button not being pressed, and another "permissible" choice which involves the button being pressed, and I want these two choices to be incomparable to the agent. Now (my mental model of) the DSM rule says: when the agent is turned on, it somehow chooses between (two plans leading to) those two options, and from then on out acts as though it has complete preferences consistent with the choice - i.e. it either (follows a plan which) makes sure the button is pressed, or (follows a plan which) makes sure the button is not pressed, and actively prevents operators from changing it. Which sounds like not-at-all what I wanted for the shutdown problem!
Agreed! The ex-ante permissibility of various options is not sufficient for shutdownability. The rest of Thornley's proposal outlines how the agent has to pick (lotteries over) trajectories, which involves more than TND.
So, roughly, we're using TND to get shutdownability, and we're using incompleteness to get TND. The reason incompleteness helps is that we want to maintain indifference to shifting probability mass between certain trajectories. And that is why we care about ex-ante permissibility.
I'm on board with the first two sentences there. And then suddenly you jump to "and that's why we care about ex-ante permissibility". Why does wanting to maintain indifference to shifting probability mass between (some) trajectories, imply that we care about ex-ante permissibility?
I don't think I've fully grokked the end-to-end story yet, but based on my current less-than-perfect understanding... we can think of Thornley's construction as a bunch of subagents indexed by t, each of which cares only about worlds where the shutdown button is pressed at time t. Then the incomplete preferences can be ~viewed as the pareto preference ordering for those agents (i.e. pareto improvements are preferred). Using something like the DSM rule to handle the incompleteness, at time zero the system-of-subagents will choose a lottery over trajectories, where the lottery is randomized by when-the-button-is-pressed (and maybe randomized by other stuff too, but that's the main thing of interest). But then that lottery over trajectories is locked in, and the system will behave from then on out as though its distribution over when-the-button-is-pressed is locked in? And it will act as though it has complete preferences over trajectory-lotteries from then on out, which is presumably not what we want? I'm not yet able to visualize exactly what the system does past that initial lock-in, so I'm not sure.
Why does wanting to maintain indifference to shifting probability mass between (some) trajectories, imply that we care about ex-ante permissibility?
The ex-ante permissible trajectories are the trajectories that the agent lacks any strict preference between. Suppose the permissible trajectories are {A,B,C}. Then, from the agent's perspective, A isn't better than B, B isn't better than A, and so on. The agent considers them all equally choiceworthy. So, the agent doesn't mind picking any one of them over any other, nor therefore switching from one lottery over them with some distribution to another lottery with some other distribution. The agent doesn't care whether it gets A versus B, versus an even chance of A or B, versus a one-third chance of A, B, or C.[1]
Suppose we didn't have multiple permissible options ex-ante. For example, if only A was permissible, then the agent would dislike shifting probability mass away from A and towards B or C—because B and C aren't among the best options.[2] So that's why we want multiple ex-ante permissible trajectories: it's the only way to maintain indifference to shifting probability mass between (those) trajectories.
[I'll respond to the stuff in your second paragraph under your longer comment.]
- ^
The analogous case with complete preferences is clearer: if there are multiple permissible options, the agent must be indifferent between them all (or else the agent would be fine picking a strictly dominated option). So if options are permissible, then . Assuming expected utility theory, we'll then of course have for any probability functions . This means the agent is indifferent to shifting probability mass between the permissible options.
- ^
This is a bit simplified but it should get the point across.
Ok, I've thought through it a little more, I think I can now articulate some confusions.
On John's-simplified-model-of-Thornley's-proposal, we have complete preference orderings over trajectories-in-which-the-button-isn't-pressed and trajectories-in-which-the-button-is-pressed, separately, but no preference between any button-pressed and button-not-pressed trajectory pair. Represented as subagents, those incomplete preferences require two subagents:
- One subagent always prefers button pressed to unpressed, is indifferent between unpressed trajectories, and has the original complete order on pressed trajectories.
- The other subagent always prefers button unpressed to pressed, is indifferent between pressed trajectories, and has the original complete order on unpressed trajectories.
In picture form (so far we've only covered the blue):
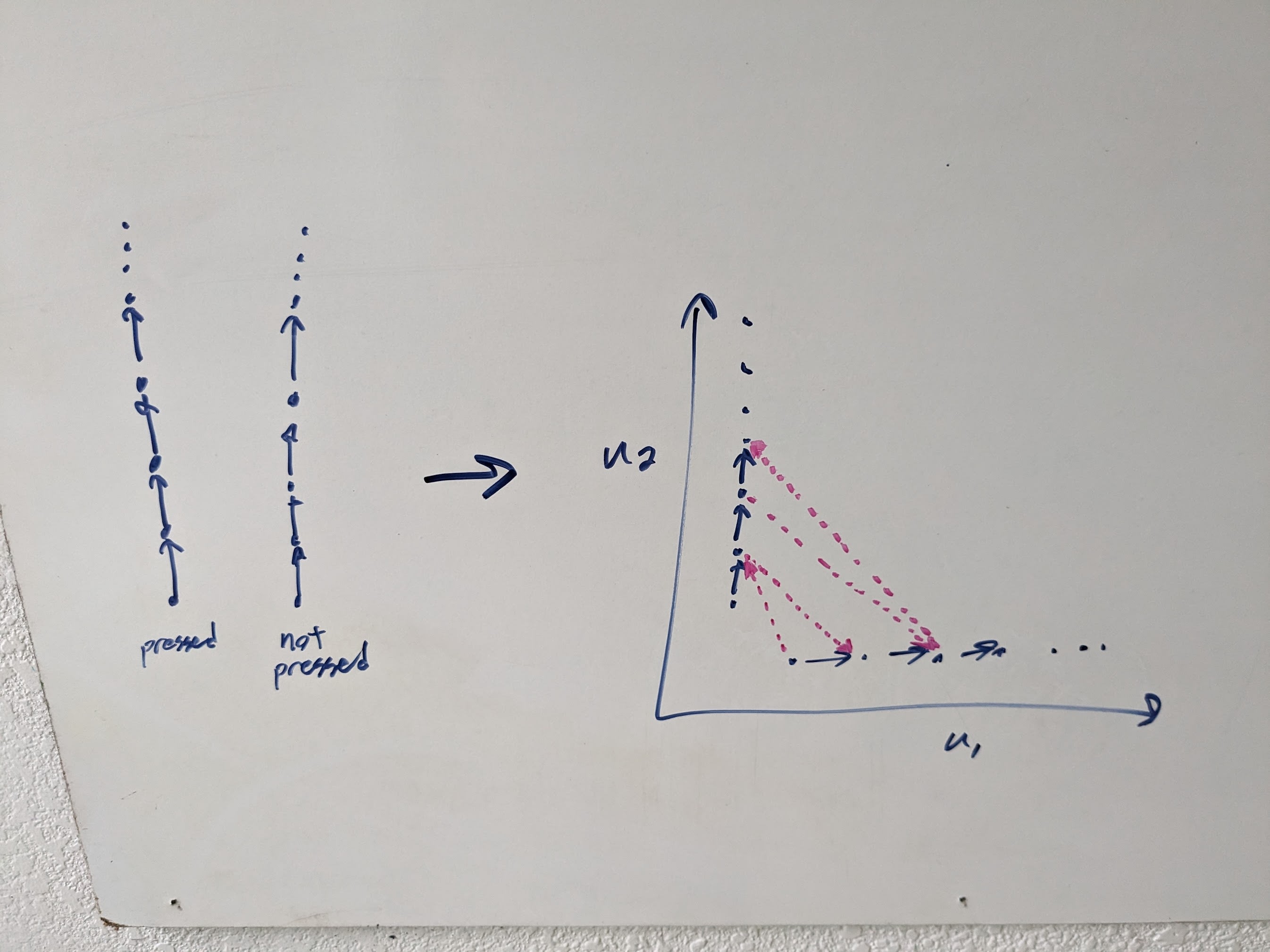
Now there's a weird-to-me part. Normally I'd say that, taking these incomplete preferences at face value, the agent looks for opportunities to pareto-improve the outcome in both pressed and unpressed worlds. But you and Thornley want to interpret "no preference" as "just choose arbitrarily/randomly" rather than "don't trade either for the other", so... this agent just chooses arbitrarily/randomly between the best-available pressed-option and the best-available unpressed-option? But that would imply that the agent is choosing (albeit arbitrarily/randomly) between button-pressed and button-unpressed, which is not what we want, so presumably you're imagining something else?
I'm going to go ahead with my usual mental model for now - i.e. "no preference" means "don't trade either for the other", so our incomplete preference system is aiming for pareto improvements. But possibly this diverges so much from what you're picturing that the below just won't be relevant.
With that flagged, on to the trammelling issue. The potential problem is that the two subagents might want to trade, so that the system sometimes tries to make the button be pressed (in cases which get relatively high pressed-utility), and sometimes tries to make the button be unpressed (in cases which get relatively high unpressed-utility). (E.g. the pink arrows in the diagram.) And... locking in a trajectory at the start doesn't seem to help that problem at all? Like, the subagents do that trading in logical time (i.e. time zero), that adds preferences, and then sometimes they lock in a plan which involves manipulating the button.
What am I missing still?
On John's-simplified-model-of-Thornley's-proposal, we have complete preference orderings over trajectories-in-which-the-button-isn't-pressed and trajectories-in-which-the-button-is-pressed, separately, but no preference between any button-pressed and button-not-pressed trajectory pair.
For the purposes of this discussion, this is right. I don't think the differences between this description and the actual proposal matter in this case.
Represented as subagents, those incomplete preferences require two subagents:
- One subagent always prefers button pressed to unpressed, is indifferent between unpressed trajectories, and has the original complete order on pressed trajectories.
- The other subagent always prefers button unpressed to pressed, is indifferent between pressed trajectories, and has the original complete order on unpressed trajectories.
I don't think this representation is quite right, although not for a reason I expect to matter for this discussion. It's a technicality but I'll mention it for completeness. If we're using Bradley's representation theorem from section 2.1., the set of subagents must include every coherent completion of the agent's preferences. E.g., suppose there are three possible trajectories. Let denote a pressed trajectory and two unpressed trajectories, where gets you strictly more coins than . Then there'll be five (ordinal) subagents, described in order of preference: , , , , and .
But you and Thornley want to interpret "no preference" as "just choose arbitrarily/randomly" rather than "don't trade either for the other", so... this agent just chooses arbitrarily/randomly between the best-available pressed-option and the best-available unpressed-option? But that would imply that the agent is choosing (albeit arbitrarily/randomly) between button-pressed and button-unpressed, which is not what we want, so presumably you're imagining something else?
Indeed, this wouldn't be good, and isn't what Thornley's proposal does. The agent doesn't choose arbitrarily between the best pressed vs unpressed options. Thornley's proposal adds more requirements on the agent to ensure this. My use of 'arbitrary' in the post is a bit misleading in that context. I'm only using it to identify when the agent has multiple permissible options available, which is what we're after to get TND. If no other requirements are added to the agent, and it's acting under certainty, this could well lead it to actually choose arbitrarily. But it doesn't have to in general, and under uncertainty and together with the rest of Thornley's requirements, it doesn't. (The requirements are described in his proposal.)
With that flagged, on to the trammelling issue. The potential problem is that the two subagents might want to trade, so that the system sometimes tries to make the button be pressed (in cases which get relatively high pressed-utility), and sometimes tries to make the button be unpressed (in cases which get relatively high unpressed-utility). (E.g. the pink arrows in the diagram.) And... locking in a trajectory at the start doesn't seem to help that problem at all? Like, the subagents do that trading in logical time (i.e. time zero), that adds preferences, and then sometimes they lock in a plan which involves manipulating the button.
I'll first flag that the results don't rely on subagents. Creating a group agent out of multiple subagents is possibly an interesting way to create an agent representable as having incomplete preferences, but this isn't the same as creating a single agent whose single preference relation happens not to satisfy completeness.
That said, I will spend some more time thinking about the subagent idea, and I do think collusion between them seems like the major initial hurdle for this approach to creating an agent with preferential gaps.
I'll first flag that the results don't rely on subagents. Creating a group agent out of multiple subagents is possibly an interesting way to create an agent representable as having incomplete preferences, but this isn't the same as creating a single agent whose single preference relation happens not to satisfy completeness.
The translation between "subagents colluding/trading" and just a plain set of incomplete preferences should be something like: if the subagents representing a set of incomplete preferences would trade with each other to emulate more complete preferences, then an agent with the plain set of incomplete preferences would precommit to act in the same way. I've never worked through the math on that, though.
I find the subagents make it a lot easier to think about, which is why I used that frame.
If we're using Bradley's representation theorem from section 2.1., the set of subagents must include every coherent completion of the agent's preferences.
Yeah, I wasn't using Bradley. The full set of coherent completions is overkill, we just need to nail down the partial order.
if the subagents representing a set of incomplete preferences would trade with each other to emulate more complete preferences, then an agent with the plain set of incomplete preferences would precommit to act in the same way
My results above on invulnerability preclude the possibility that the agent can predictably be made better off by its own lights through an alternative sequence of actions. So I don't think that's possible, though I may be misreading you. Could you give an example of a precommitment that the agent would take? In my mind, an example of this would have to show that the agent (not the negotiating subagents) strictly prefers the commitment to what it otherwise would've done according to DSM etc.
Yeah, I wasn't using Bradley. The full set of coherent completions is overkill, we just need to nail down the partial order.
I agree the full set won't always be needed, at least when we're just after ordinal preferences, though I personally don't have a clear picture of when exactly that holds.
(I'm still processing confusion here - there's some kind of ontology mismatch going on. I think I've nailed down one piece of the mismatch enough to articulate it, so maybe this will help something click or at least help us communicate.
Key question: what are the revealed preferences of the DSM agent?
I think part of the confusion here is that I've been instinctively trying to think in terms of revealed preferences. But in the OP, there's a set of input preferences and a decision rule which is supposed to do well by those input preferences, but the revealed preferences of the agent using the rule might (IIUC) differ from the input preferences.
Connecting this to corrigibility/shutdown/Thornley's proposal: the thing we want, for a shutdown proposal, is a preferential gap in the revealed preferences of the agent. I.e. we want the agent to never spend resources to switch between button pressed/unpressed, but still have revealed preferences between different pressed states and between different unpressed states.
So the key question of interest is: do trammelling-style phenomena induce completion of the agent's revealed preferences?
Does that immediately make anything click for you?)
That makes sense, yeah.
Let me first make some comments about revealed preferences that might clarify how I'm seeing this. Preferences are famously underdetermined by limited choice behaviour. If A and B are available and I pick A, you can't infer that I like A more than B — I might be indifferent or unable to compare them. Worse, under uncertainty, you can't tell why I chose some lottery over another even if you assume I have strict preferences between all options — the lottery I choose depends on my beliefs too. In expected utility theory, beliefs and preferences together induce choice, so if we only observe a choice, we have one equation in two unknowns.[1] Given my choice, you'd need to read my mind's probabilities to be able to infer my preferences (and vice versa).[2]
In that sense, preferences (mostly) aren't actually revealed. Economists often assume various things to apply revealed preference theory, e.g. setting beliefs equal to 'objective chances', or assuming a certain functional form for the utility function.
But why do we care about preferences per se, rather than what's revealed? Because we want to predict future behaviour. If you can't infer my preferences from my choices, you can't predict my future choices. In the example above, if my 'revealed preference' between A and B is that I prefer A, then you might make false predictions about my future behaviour (because I might well choose B next time).
Let me know if I'm on the right track for clarifying things. If I am, could you say how you see trammelling/shutdown connecting to revealed preferences as described here, and I'll respond to that?
Feels like we're making some progress here.
Let's walk through more carefully why revealed preferences are interesting in the shutdown problem. (I'm partly thinking as I write, here.) Suppose that, at various times, the agent is offered opportunities to spend resources in order to cause the button to be pushed/unpushed. We want the agent to turn down such opportunities, in both directions - implying either indifference or lack of preference in any revealed preferences. Further, we do want the agent to spend resources to cause various different outcomes within the button-pressed or button-unpressed worlds, so there's nontrivial revealed preference ordering within button-pressed worlds and within button-unpressed worlds. But if the agent is to turn down costly opportunities to cause the button to be pressed/unpressed, and those opportunities jump between enough different pressed-outcome and unpressed-outcome pairs (which themselves each have nontrivial revealed preferences), then there's going to be a revealed preference gap.
Upshot: (one way to frame) the reason that the shutdown problem is difficult/interesting in the first place, is that the desired behavior implies a revealed preference gap. Insofar as e.g. any standard expected utility maximizer cannot have a revealed preference gap, such standard EU maximizers cannot behave the way we want. (This frame is new-to-me, so thankyou.)
(Note that that's all totally compatible with revealed preferences usually being very underdetermined! The desired behavior nails things down enough that any assignment of revealed preferences must have a preferential gap. The question is whether we can come up with some agent with a stable gap in its revealed preferences.)
(Also note that the story above routed through causal intervention/counterfactuals to probe revealed preference, so that does open up a lot of extra ways-of-revealing. Not sure if that's relevant yet.)
Now bringing this back to DSM... I think the question I'm interested in is: "do trammelling-style issues imply that DSM agents will not have a revealed preference gap (under reasonable assumptions about their environment and capabilities)?". If the answer is "yes" - i.e. if trammelling-style issues do imply that sufficiently capable DSM agents will have no revealed preference gaps - then that would imply that capable DSM agents cannot display the shutdown behavior we want.
On the other hand, if DSM agents can have revealed preference gaps, without having to artificially limit the agents' capabilities or the richness of the environment, then that seems like it would circumvent the main interesting barrier to the shutdown problem. So I think that's my main crux here.
Great, I think bits of this comment help me understand what you're pointing to.
the desired behavior implies a revealed preference gap
I think this is roughly right, together with all the caveats about the exact statements of Thornley's impossibility theorems. Speaking precisely here will be cumbersome so for the sake of clarity I'll try to restate what you wrote like this:
- Useful agents satisfying completeness and other properties X won't be shutdownable.
- Properties X are necessary for an agent to be useful.
- So, useful agents satisfying completeness won't be shutdownable.
- So, if a useful agent is shutdownable, its preferences are incomplete.
This argument would let us say that observing usefulness and shutdownability reveals a preferential gap.
I think the question I'm interested in is: "do trammelling-style issues imply that DSM agents will not have a revealed preference gap (under reasonable assumptions about their environment and capabilities)?"
A quick distinction: an agent can (i) reveal p, (ii) reveal ¬p, or (iii) neither reveal p nor ¬p. The problem of underdetermination of preference is of the third form.
We can think of some of the properties we've discussed as 'tests' of incomparability, which might or might not reveal preferential gaps. The test in the argument just above is whether the agent is useful and shutdownable. The test I use for my results above (roughly) is 'arbitrary choice'. The reason I use that test is that my results are self-contained; I don't make use of Thornley's various requirements for shutdownability. Of course, arbitrary choice isn't what we want for shutdownability. It's just a test for incomparability that I used for an agent that isn't yet endowed with Thornley's other requirements.
The trammelling results, though, don't give me any reason to think that DSM is problematic for shutdownability. I haven't formally characterised an agent satisfying DSM as well as TND, Stochastic Near-Dominance, and so on, so I can't yet give a definitive or exact answer to how DSM affects the behaviour of a Thornley-style agent. (This is something I'll be working on.) But regarding trammelling, I think my results are reasons for optimism if anything. Even in the least convenient case that I looked at—awareness growth—I wrote this in section 3.3. as an intuition pump:
we’re simply picking out the best prospects in each class. For instance, suppose prospects were representable as pairs that are comparable iff the -values are the same, and then preferred to the extent that is large. Then here’s the process: for each value of , identify the options that maximise . Put all of these in a set. Then choice between any options in that set will always remain arbitrary; never trammelled.
That is, we retain the preferential gap between the options we want a preferential gap between.
[As an aside, the description in your first paragraph of what we want from a shutdownable agent doesn't quite match Thornley's setup; the relevant part to see this is section 10.1. here.]
I'll first flag that the results don't rely on subagents. Creating a group agent out of multiple subagents is possibly an interesting way to create an agent representable as having incomplete preferences, but this isn't the same as creating a single agent whose single preference relation happens not to satisfy completeness.
Flagging here that I don't think the subagent framing is super important and/or necessary for "collusion" to happen. Even if the "outer" agent isn't literally built from subagents, "collusion" can still occur in the sense that it [the outer agent] can notice that its (incomplete) preferences factorize, in a way that allows it to deliberately trade particular completions of them against each other and thereby acquire more resources. The outer agent would then choose to do this for basically the same reason that a committee of subagents would: to acquire more resources for itself as a whole, without disadvantaging any of the completions under consideration.
My results above on invulnerability preclude the possibility that the agent can predictably be made better off by its own lights through an alternative sequence of actions. So I don't think that's possible, though I may be misreading you. Could you give an example of a precommitment that the agent would take? In my mind, an example of this would have to show that the agent (not the negotiating subagents) strictly prefers the commitment to what it otherwise would've done according to DSM etc.
On my understanding, the argument isn’t that your DSM agent can be made better off, but that the reason it can’t be made better off is because it is engaging in trammeling/“collusion”, and that the form of “trammeling” you’ve ruled out isn’t the useful kind.
As far as an example goes, consider a sequence of actions which, starting from an unpressed world state, routes through a pressed world state (or series of pressed world states), before eventually returning to an unpressed world state with higher utility than the initial state.
(The real-world context of such a sequence shouldn’t be too relevant to a theoretical example like this, but if you had to imagine something, you could imagine a “memory gambit”-esque stratagem, where the agent spends some time inactive in order to avoid detection, but has set things up in advance to eventually reactivate itself under more favorable circumstances. Again, the plausibility of the scenario isn’t super relevant here.)
If your proposed DSM agent passes up this action sequence on the grounds that some of the intermediate steps need to bridge between “incomparable” pressed/unpressed trajectories, then it does in fact pass up the certain gain. Conversely, if it doesn’t pass up such a sequence, then its behavior is the same as that of a set of negotiating subagents cooperating in order to form a larger macroagent.
On my understanding, the argument isn’t that your DSM agent can be made better off, but that the reason it can’t be made better off is because it is engaging in trammeling/“collusion”, and that the form of “trammeling” you’ve ruled out isn’t the useful kind.
I don't see how this could be right. Consider the bounding results on trammelling under unawareness (e.g. Proposition 10). They show that there will always be a set of options between which DSM does not require choosing one over the other. Suppose these are X and Y. The agent will always be able to choose either one. They might end up always choosing X, always Y, switching back and forth, whatever. This doesn't look like the outcome of two subagents, one preferring X and the other Y, negotiating to get some portion of the picks.
As far as an example goes, consider a sequence of actions which, starting from an unpressed world state, routes through a pressed world state (or series of pressed world states), before eventually returning to an unpressed world state with higher utility than the initial state.
Forgive me; I'm still not seeing it. For coming up with examples, I think for now it's unhelpful to use the shutdown problem, because the actual proposal from Thornley includes several more requirements. I think it's perfectly fine to construct examples about trammelling and subagents using something like this: A is a set of options with typical member . These are all comparable and ranked according to their subscripts. That is, is preferred to , and so on. Likewise with set B. And all options in A are incomparable to all options in B.
If your proposed DSM agent passes up this action sequence on the grounds that some of the intermediate steps need to bridge between “incomparable” pressed/unpressed trajectories, then it does in fact pass up the certain gain. Conversely, if it doesn’t pass up such a sequence, then its behavior is the same as that of a set of negotiating subagents cooperating in order to form a larger macroagent.
This looks to me like a misunderstanding that I tried to explain in section 3.1. Let me know if not, though, ideally with a worked-out example of the form: "here's the decision tree(s), here's what DSM mandates, here's why it's untrammelled according to the OP definition, and here's why it's problematic."
This looks to me like a misunderstanding that I tried to explain in section 3.1. Let me know if not, though, ideally with a worked-out example of the form: "here's the decision tree(s), here's what DSM mandates, here's why it's untrammelled according to the OP definition, and here's why it's problematic."
I don't think I grok the DSM formalism enough to speak confidently about what it would mandate, but I think I see a (class of) decision problem where any agent (DSM or otherwise) must either pass up a certain gain, or else engage in "problematic" behavior (where "problematic" doesn't necessarily mean "untrammeled" according to the OP definition, but instead more informally means "something which doesn't help to avoid the usual pressures away from corrigibility / towards coherence"). The problem in question is essentially the inverse of the example you give in section 3.1:
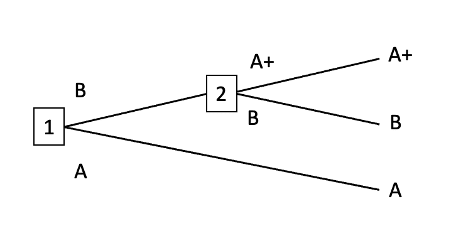
Consider an agent tasked with choosing between two incomparable options A and B, and if it chooses B, it will be further presented with the option to trade B for A+, where A+ is incomparable to B but comparable (and preferable) to A.
(I've slightly modified the framing to be in terms of trades rather than going "up" or "down", but the decision tree is isomorphic.)
Here, A+ isn't in fact "strongly maximal" with respect to A and B (because it's incomparable to B), but I think I'm fairly confident in declaring that any agent which foresees the entire tree in advance, and which does not pick B at the initial node (going "down", if you want to use the original framing), is engaging in a dominated behavior—and to the extent that DSM doesn't consider this a dominated strategy, DSM's definitions aren't capturing a useful notion of what is "dominated" and what isn't.
Again, I'm not claiming this is what DSM says. You can think of me as trying to run an obvious-to-me assertion test on code which I haven't carefully inspected, to see if the result of the test looks sane. But if a (fully aware/non-myopic) DSM agent does constrain itself into picking B ("going down") in the above example, despite the prima facie incomparability of {A, A+} and {B}, then I would consider this behavior problematic once translated back into the context of real-world shutdownability, because it means the agent in question will at least in some cases act in order to influence whether the button is pressed.
(The hope behind incomplete preferences, after all, is that an agent whose preferences over world-states can be subdivided into "incomparability classes" will only ever act to improve its lot within the class of states it finds itself in to begin with, and will never act to shift—or prevent itself from being shifted—to a different incomparability class. I think the above example presents a deep obstacle to this hope, however. Very roughly speaking, if the gaps in the agent's preferences can be bridged via certain causal pathways, then a (non-myopic) agent which does not exploit these pathways to its own benefit will notice itself failing to exploit them, and self-modify to stop doing that.)
In your example, DSM permits the agent to end up with either A+ or B. Neither is strictly dominated, and neither has become mandatory for the agent to choose over the other. The agent won't have reason to push probability mass from one towards the other.
You can think of me as trying to run an obvious-to-me assertion test on code which I haven't carefully inspected, to see if the result of the test looks sane.
This is reasonable but I think my response to your comment will mainly involve re-stating what I wrote in the post, so maybe it'll be easier to point to the relevant sections: 3.1. for what DSM mandates when the agent has beliefs about its decision tree, 3.2.2 for what DSM mandates when the agent hadn't considered an actualised continuation of its decision tree, and 3.3. for discussion of these results. In particular, the following paragraphs are meant to illustrate what DSM mandates in the least favourable epistemic state that the agent could be in (unawareness with new options appearing):
It seems we can’t guarantee non-trammelling in general and between all prospects. But we don’t need to guarantee this for all prospects to guarantee it for some, even under awareness growth. Indeed, as we’ve now shown, there are always prospects with respect to which the agent never gets trammelled, no matter how many choices it faces. In fact, whenever the tree expansion does not bring about new prospects, trammelling will never occur (Proposition 7). And even when it does, trammelling is bounded above by the number of comparability classes (Proposition 10).
And it’s intuitive why this would be: we’re simply picking out the best prospects in each class. For instance, suppose prospects were representable as pairs that are comparable iff the -values are the same, and then preferred to the extent that is large. Then here’s the process: for each value of , identify the options that maximise . Put all of these in a set. Then choice between any options in that set will always remain arbitrary; never trammelled.
In your example, DSM permits the agent to end up with either A+ or B. Neither is strictly dominated, and neither has become mandatory for the agent to choose over the other. The agent won't have reason to push probability mass from one towards the other.
But it sounds like the agent's initial choice between A and B is forced, yes? (Otherwise, it wouldn't be the case that the agent is permitted to end up with either A+ or B, but not A.) So the presence of A+ within a particular continuation of the decision tree influences the agent's choice at the initial node, in a way that causes it to reliably choose one incomparable option over another.
Further thoughts: under the original framing, instead of choosing between A and B (while knowing that B can later be traded for A+), the agent instead chooses whether to go "up" or "down" to receive (respectively) A, or a further choice between A+ and B. It occurs to me that you might be using this representation to argue for a qualitative difference in the behavior produced, but if so, I'm not sure how much I buy into it.
For concreteness, suppose the agent starts out with A, and notices a series of trades which first involves trading A for B, and then B for A+. It seems to me that if I frame the problem like this, the structure of the resulting tree should be isomorphic to that of the decision problem I described, but not necessarily the "up"/"down" version—at least, not if you consider that version to play a key role in DSM's recommendation.
(In particular, my frame is sensitive to which state the agent is initialized in: if it is given B to start, then it has no particular incentive to want to trade that for either A or A+, and so faces no incentive to trade at all. If you initialize the agent with A or B at random, and institute the rule that it doesn't trade by default, then the agent will end up with A+ when initialized with A, and B when initialized with B—which feels a little similar to what you said about DSM allowing both A+ and B as permissible options.)
It sounds like you want to make it so that the agent's initial state isn't taken into account—in fact, it sounds like you want to assign values only to terminal nodes in the tree, take the subset of those terminal nodes which have maximal utility within a particular incomparability class, and choose arbitrarily among those. My frame, then, would be equivalent to using the agent's initial state as a tiebreaker: whichever terminal node shares an incomparability class with the agent's initial state will be the one the agent chooses to steer towards.
...in which case, assuming I got the above correct, I think I stand by my initial claim that this will lead to behavior which, while not necessarily "trammeling" by your definition, is definitely consequentialist in the worrying sense: an agent initialized in the "shutdown button not pressed" state will perform whatever intermediate steps are needed to navigate to the maximal-utility "shutdown button not pressed" state it can foresee, including actions which prevent the shutdown button from being pressed.
Good question. They implicitly assume a dynamic choice principle and a choice function that leaves the agent non-opportunistic.
- Their dynamic choice principle is something like myopia: the agent only looks at their node's immediate successors and, if a successor is yet another choice node, the agent represents it as some 'default' prospect.
- Their choice rule is something like this: the agent assigns some natural 'default' prospect and deviates from it iff it prefers some other prospect. (So if some prospect is incomparable to the default, it's never chosen.)
These aren't the only approaches an agent can employ, and that's where it fails. It's wrong to conclude that "non-dominated strategy implies utility maximization" since we know from section 2 that we can achieve non-domination without completeness—by using a different dynamic choice principle and choice function.
That is a fantastic answer, thank you. Do you think that there's any way your post could be wrong? For instance, "[letting] decision trees being the main model of an agent's environment", as per JohnWentworth in a discussion with EJT[1] where he makes a similair critique to your point about their implicit dynamic choice principle?
- ^
See the comments section of this post: https://www.lesswrong.com/posts/bzmLC3J8PsknwRZbr/why-not-subagents
Thanks for saying!
This is an interesting topic. Regarding the discussion you mention, I think my results might help illustrate Elliott Thornley's point. John Wentworth wrote:
That makes me think that the small decision trees implicitly contain a lot of assumptions that various trades have zero probability of happening, which is load-bearing for your counterexamples. In a larger world, with a lot more opportunities to trade between various things, I'd expect that sort of issue to be much less relevant.
My results made no assumptions about the size or complexity of the decision trees, so I don't think this itself is a reason to doubt my conclusion. More generally, if there exists some Bayesian decision tree that faithfully represents an agent's decision problem, and the agent uses the appropriate decision principles with respect to that tree, then my results apply. The existence of such a representation is not hindered by the number of choices, the number of options, or the subjective probability distributions involved.
I think my results under unawareness (section 3) are particularly likely to be applicable to complex real-world decision problems. The agent can be entirely wrong about their actual decision tree—e.g., falsely assigning probability zero to events that will occur—and yet appropriate opportunism remains and trammelling is bounded. This is because any suboptimal decision by an agent in these kinds of cases is a product of its epistemic state; not its preferences. Whether the agent's preferences are complete or not, it will make wrong turns in the same class of situations. The globally-DSM choice function will guarantee that the agent couldn't have done better given its knowledge and values, even if the agent's model of the world is wrong.
Am I correct in thinking that with Strong Maximality and resolute choice applied to a single sweetening money pump, an agent will never take the bottom pathway, because it eliminates the A plan because A+ plan is strictly preferred?
If so, what's an example of a decision tree where the actions of an agent with incomplete preferences can't be represented as an agent with complete preferences?
Yes that's right (regardless of whether it's resolute or whether it's using 'strong' maximality).
A sort of of a decision tree where the agent isn't representable as having complete preferences is the one you provide here. We can even put the dynamic aspect aside to make the point. Suppose that the agent is fact inclined to pick A+ over A, but doesn't favour or disfavour B to either one. Here's my representation: maximal choice with A+ A and B A,A+. As a result, I will correctly predict its behaviour: it'll choose something other than A.
Can I also do this with another representation, using a complete preference relation? Let's try out indifference between A+ and B. I'd indeed make the same prediction in this particular case. But suppose the agent were next to face a choice between A+, B, and B+ (where the latter is a sweetening of B). By transitivity, we know B+ A+, and so this representation would predict that B+ would be chosen for sure. But this is wrong, since in fact the agent is not inclined to favour B-type prospects over A-type prospects. In contrast, the incomplete representation doesn't make this error.
Summing up: the incomplete representation works for {A+,A,B} and {A+,B,B+} while the only complete one that also works for the former fails for the latter.
it'll choose something other than A.
Are you aware that this is incompatible with Thornley's ideas about incomplete preferences? Thornley's decision rule might choose A. [Edit: I retract this, it's wrong].
But suppose the agent were next to face a choice
If the choices are happening one after the other, are the preferences over tuples of outcomes? Or are the two choices in different counterfactuals? Or is it choosing an outcome, then being offered another outcome set that it could to replace it with?
VNM is only well justified when the preferences are over final outcomes, not intermediate states. So if your example contains preferences over intermediate states, then it confuses the matter because we can attribute the behavior to those preferences rather than incompleteness.
My use of 'next' need not be read temporally, though it could be. You might simply want to define a transitive preference relation for the agent over {A,A+,B,B+} in order to predict what it would choose in an arbitrary static decision problem. Only the incomplete one I described works no matter what the decision problem ends up being.
As a general point, you can always look at a decision ex post and back out different ways to rationalise it. The nontrivial task is here prediction, using features of the agent.
If we want an example of sequential choice using decision trees (rather than repeated 'de novo' choice through e.g. unawareness), it'll be a bit more cumbersome but here goes.
Intuitively, suppose the agent first picks from {A,B+} and then, in addition, from {A+,B}. It ends up with two elements from {A,A+,B,B+}. Stated within the framework:
- The set of possible prospects is X = {A,A+B,B+}×{A,A+B,B+}, where elements are pairs.
- There's a tree where, at node 1, the agent picks among paths labeled A and B+.
- If A is picked, then at the next node, the agent picks from terminal prospects {(A,A+),(A,B)}. And analogously if path B+ is picked.
- The agent has appropriately separable preferences: (x,y) (x',y') iff x x'' and y y'' for some permutation (x'',y'') of (x'y'), where is a relation over components.
Then (A+,x) (A,x) while (A,x) (B,x) for any prospect component x, and so on for other comparisons. This is how separability makes it easy to say "A+ is preferred to A" even though preferences are defined over pairs in this case. I.e., we can construct over pairs out of some over components.
In this tree, the available prospects from the outset are (A,A+), (A,B), (B+,A+), (B+,B).
Using the same as before, the (dynamically) maximal ones are (A,A+), (B+,A+), (B+,B).
But what if, instead of positing incomparability between A and B+ we instead said the agent was indifferent? By transitivity, we'd infer A B and thus A+ B. But then (B+,B) wouldn't be maximal. We'd incorrectly rule out the possibility that the agent goes for (B+,B).
The description of how sequential choice can be defined is helpful, I was previously confused by how this was supposed to work. This matches what I meant by preferences over tuples of outcomes. Thanks!
We'd incorrectly rule out the possibility that the agent goes for (B+,B).
There's two things we might want from the idea of incomplete preferences:
- To predict the actions of agents.
- Because complete agents behave dangerously sometimes, and we want to design better agents with different behaviour.
I think modelling an agent as having incomplete preferences is great for (1). Very useful. We make better predictions if we don't rule out the possibility that the agent goes for B after choosing B+. I think we agree here.
For (2), the relevant quote is:
As a general point, you can always look at a decision ex post and back out different ways to rationalise it. The nontrivial task is here prediction, using features of the agent.
If we can always rationalise a decision ex post as being generated by a complete agent, then let's just build that complete agent. Incompleteness isn't helping us, because the behaviour could have been generated by complete preferences.
Are you aware that this is incompatible with Thornley's ideas about incomplete preferences? Thornley's decision rule might choose A.
I retract this part of the comment. I misinterpreted the comment that I linked to. Seems like they are compatible.
This is extraordinarily impressive, even with the limits on your proofs. I'd argue this is a possible situation where assuming certain potentially minor things work out, this could be a great example of an MIRI-inspired success, and one of the likeliest to transfer to future models of AI. Given that we usually want AIs to be able to be shutdownable without compromising on the most useful parts of expected utility maximization, this is pretty extraordinary as a result.
Section 3 begins with a conceptual argument suggesting that DSM-based choice under uncertainty will not, even behaviourally, effectively alter the agent’s preferences over time.
Hold up, does this mean you don't have a proof that agents who are Certain about their Tree are trammelled or not?
EDIT: Ah, I see you confirm that in section 3. Good to know.
I take certainty to be a special case of uncertainty. Regarding proof, the relevant bit is here:
This argument does not apply when the agent is unaware of the structure of its decision tree, so I provide some formal results for these cases which bound the extent to which preferences can de facto be completed. ... These results apply naturally to cases in which agents are unaware of the state space, but readers sceptical of the earlier conceptual argument can re-purpose them to make analogous claims in standard cases of certainty and uncertainty.
It's the set of elementary states.
So is an event (a subset of elementary states, ).
E.g., we could have be all the possible worlds; be the possible worlds in which featherless bipeds evolved; and be our actual world.
No, the codomain of gamma is the set of (distributions over) consequences.
Hammond's notation is inspired by the Savage framework in which states and consequences are distinct. Savage thinks of a consequence as the result of behaviour or action in some state, though this isn't so intuitively applicable in the case of decision trees. I included it for completeness but I don't use the gamma function explicitly anywhere.
The LessWrong Review runs every year to select the posts that have most stood the test of time. This post is not yet eligible for review, but will be at the end of 2024. The top fifty or so posts are featured prominently on the site throughout the year.
Hopefully, the review is better than karma at judging enduring value. If we have accurate prediction markets on the review results, maybe we can have better incentives on LessWrong today. Will this post make the top fifty?
And, second, the agent will continually implement that plan, even if this makes it locally choose counter-preferentially at some future node.
Nitpick: IIRC, McClennen never talks about counter-preferential choice. Rather, that's Gauthier's (1997) approach to resoluteness.
as devised by Bryan Skyrms and Gerald Rothfus (cf Rothfus 2020b).
Found a typo: it is supposed to be Gerard. (It is also misspelt in the reference list.)
Produced as part of the SERI ML Alignment Theory Scholars Program - Summer 2023 Cohort. My thanks to Eric Chen, Elliott Thornley, and John Wentworth for invaluable discussion and comments on earlier drafts. All errors are mine.
This article presents a few theorems about the invulnerability of agents with incomplete preferences. Elliott Thornley’s (2023) proposed approach to the AI shutdown problem relies on these preferential gaps, but John Wentworth and David Lorell have argued that they make agents play strictly dominated strategies.[1] I claim this is false.
Summary
Suppose there exists a formal description of an agent that willingly shuts down when a certain button is pressed. Elliott Thornley’s (2023) Incomplete Preference Proposal aims to offer such a description. It’s plausible that, for it to constitute a promising approach to solving the AI shutdown problem, this description also needs to (i) permit the agent to be broadly capable and (ii) assure us that the agent will remain willing to shut down as time passes. This article formally derives a set of sufficient conditions for an agent with incomplete preferences to satisfy properties relevant to (i) and (ii).
A seemingly relevant condition for an agent to be capably goal-directed is that it avoids sequences of actions that foreseeably leave it worse off.[2] I will say that an agent satisfying this condition is invulnerable. This is related to two intuitive conditions. The weaker one is unexploitability: that the agent cannot be forcibly money pumped (i.e., compelled by its preferences to sure loss). The stronger condition is opportunism: that the agent never accepts sure losses or foregoes sure gains.[3]
To achieve this, I propose a dynamic choice rule for agents with incomplete preferences. This rule, Dynamic Strong Maximality (DSM), requires that the agent consider the available plans that are acceptable at the time of choosing and, among these, pick any plan that wasn’t previously strictly dominated by any other such plan. I prove in section 2 that DSM-based backward induction is sufficient for invulnerability, even under uncertainty.
Having shown that incompleteness does not imply that agents will pursue dominated strategies, I consider the issue of whether DSM leads agents to act as if their preferences were complete. Section 3 begins with a conceptual argument suggesting that DSM-based choice under uncertainty will not, even behaviourally, effectively alter the agent’s preferences over time. This argument does not apply when the agent is unaware of the structure of its decision tree, so I provide some formal results for these cases which bound the extent to which preferences can de facto be completed.
These results show that there will always be sets of options with respect to which the agent never completes its preferences. This holds no matter how many choices it faces. In particular, if no new options appear in the decision tree, then no amount of completion will occur; and if new options do appear, the amount of completion is permanently bounded above by the number of mutually incomparable options. These results apply naturally to cases in which agents are unaware of the state space, but readers sceptical of the earlier conceptual argument can re-purpose them to make analogous claims in standard cases of certainty and uncertainty. Therefore, imposing DSM as a choice rule can get us invulnerability without sacrificing incompleteness, even in the limit.
1. Incompleteness and Choice
The aim of this brief section is to show that the results that follow in section 2 do not require transitivity. Some question the requirement of transitivity when preferences are incomplete (cf Bradley 2015, p. 3), but if that doesn’t apply to you, a quick skim of this section will provide enough context for the rest.
1.1. Suzumura Consistency
Requiring that preferences be transitive may require that they be complete. To see this, notice that the weak preference relation ⪰ on a set of prospects X is transitive just in case ∀α,β,γ∈X, α⪰β and β⪰γ implies α⪰γ. Suppose an agent does weakly prefer α to β and β to γ but has no preference between α and γ. Then transitivity is violated. Suzumura (1976) proposes a weakening of transitivity for agents with incomplete preferences, which allows for such preferences while preserving some desirable properties. We will say that a weak preference relation is strongly acyclic just in case
(Strong Acyclicity) ∀α1,...,αn∈X, α1⪰...⪰αn implies αn⊁α1.
We'll say that an agent whose preferences satisfy this property is Suzumura consistent. Bossert and Suzumura (2010) show that such an agent has some noteworthy features:
Preferences that are incomplete may also be intransitive. Whether or not transitivity is a rationality condition, strong acyclicity is weaker but preserves some desirable properties. Below I will mostly just assume strong acyclicity. But since transitivity implies strong acyclicity, all the (sufficiency) results likewise apply to agents with transitive preferences.
1.2. Strong Maximality
Bradley (2015) proposes a choice rule for Suzumura consistent agents which differs from the standard condition—Maximality—for agents with incomplete preferences.[4] This rule—Strong Maximality—effectively asks the agent to eliminate dominated alternatives in the following way: eliminate any options that you strictly disprefer to any others, then if you are indifferent between any remaining options and any eliminated ones, eliminate those as well. To state the rule formally, we define a sequence ⟨¯Cτ(A)⟩∞τ=0 satisfying
¯C0(A)={α∈A:β≻α∃β∈A} and ¯Cτ(A)={α∈A:[β∼α]∧[β∈¯Cτ−1(A)]∃β∈A} whenever τ≥1
for any nonempty set of prospects A. We can then state the rule as
(Strong Maximality) CSM(A)={α∈A:α∉⋃∞τ=0¯Cτ(A)}.
Let’s see intuitively what this rule captures. Suppose α≻β and β∼γ but α⋈/γ.[5] The traditional maximality rule implies that C({α,β,γ})={α,γ}. But strong maximality simply outputs {α}. This is intuitive: don’t pick an option that’s just as bad as an option you dislike. And, more importantly, Theorem 2 of Bradley (2015) shows that Suzumura consistency is both necessary and sufficient for decisive, strongly maximal choice.[6]
2. Uncertain Dynamic Choice
In this section I prove some theorems about the performance of agents with incomplete preferences in dynamic settings. I will amend strong maximality slightly to adapt it to dynamic choice, and show that this is sufficient to guarantee the invulnerability of these agents, broadly construed. I will say that an agent is invulnerable iff it is both unexploitable and opportunistic.
An agent is unexploitable just in case it is immune to all forcing money pumps. These are sequences of decisions through which an agent is compelled by their own preferences to sure loss. An agent is opportunistic just in case it is immune to all non-forcing money pumps. These are situations in which sure loss (or missed gain) is merely permissible, according to an agent’s preferences.
A few aspects of the broad approach are worth flagging. Normative decision theory has not settled on an ideal set of norms to govern dynamic choice. I will therefore provide results with respect to each of the following three dynamic choice principles: naivety, sophistication, and resoluteness. (More details below.) Agents will in general behave differently depending on which principle they follow. So, evaluating the behaviour resulting from an agent’s preferences should, at least initially, be done separately for each dynamic choice principle.
2.1. Framework
The notation going forward comes from an edited version of Hammond's (1988) canonical construction of Bayesian decision trees. I will only describe the framework briefly, so I’ll refer interested readers to Rothfus (2020a) section 1.6. for discussion.
Definition 1 A decision tree is an eight-tuple ⟨N,C,N,X,N+(⋅),n0,S(⋅),γ(⋅)⟩ where
Definition 2 A set of plans available at node n of tree T, denoted Ω(T,n), contains the propositions and continuations consistent with the agent being at that node. Formally,
I will begin the discussion below with dynamic choice under certainty, but to set up the more general results, I will now lay out the framework for uncertain choice as well and specify later what is assumed. To start, it will be useful to have a representation theorem for our incomplete agents.
Imprecise Bayesianism (Bradley 2017, Theorem 37) Let ⪰ be a non-trivial preference relation on a complete and atomless Boolean algebra of prospects Ω=⟨X,⊨⟩, which has a minimal coherent extension on Ω that is both continuous and impartial.[8] Then there exists a unique rationalising state of mind, S={⟨Pi,Vi⟩}, on Ω containing all pairs of probability and desirability measures jointly consistent with these preferences, in the sense that for all α,β∈Ω∖{⊥},
α⪰β⟺Vi(α)≥Vi(β)∀Vi∈S.
This theorem vindicates the claim that the state of mind of a broad class of rational agents with incomplete preferences can be represented by a set of pairs of probability and desirability functions. Although this theorem applies to imprecise credences, I’ll work with the special case of precise beliefs throughout. This will simplify the analysis. I’ll therefore use the following notation going forward: Z={i∈N:Vi∈S}.
Next, I define some conditions that will be invoked in some of the derivations.
Definition 3 Material Planning: For a plan to specify choices across various contingencies, I formalise a planning conditional as follows. Let n be a natural node and nj∈N+(n) a possible realisation of it. Here, a plan
p(n)=S(n)∧⋀|N+(n)|j=1[S(nj)→S(zj)]
assigns a chosen continuation, zj∈N+(nj), to each possible realisation of n. When preferences are complete, a plan at a natural node is then evaluated as follows:
Vn(p)=∑|N+(n)|j=1Vn(zj)P(nj|p(n)).
This is a natural extension of Jeffrey’s equation. And when preferences are incomplete:
p⪰np′ iff Vin(p)≥Vin(p′)∀i∈Z.
This makes use of Bradley’s representation theorem for Imprecise Bayesianism.
Definition 4 Preference Stability (Incomplete): For all nodes na and nb and plans p where p(na)=p(nb), we have Vina(p)=Vinb(p)∀i∈Z.
Definition 5 Plan-Independent Probabilities (PIP): For any decision tree T in which n is a natural node, n′∈N+(n) is a realisation of n, and p∈Ω(T,n), P(n′|p(n))=P(n′|n).
The results can now be stated. I will include proofs of the central claims in the main text; others are relegated to the appendix. I suggest scrolling past them if you aren’t particularly surprised by the result.
2.2. Myopia
Let’s begin with the simplest case of exploitation. We can stay silent on which dynamic choice principle to employ here: even if our agent is myopic, it will never be vulnerable to forcing money pumps under certainty. This follows immediately from Suzumura consistency since this guarantees that the agent never has a strict preference in a cycle of weak preferences.
Proposition 1 Suzumura consistent agents myopically applying strong maximality are unexploitable under certainty. [Proof.]
Two points are worth noting about the simple proof. First, it relies on strict preferences. This is because, if a money pump must go through a strongly maximal choice set with multiple elements (due to indifference or appropriate incomparability), it is necessarily non-forcing. That's the topic of the next section. Second, the proof doesn't rely on foresight. Myopia is an intentionally weak assumption that lets us show that no knowledge of the future is required for Suzumura consistent agents to avoid exploitation via these forcing money pumps.
2.3. Naive Choice
Although Suzumura consistent agents using strong maximality can't be forced into money pumps, concern remains. Such an agent might still incidentally do worse by their own lights. That is, it remains vulnerable to non-forcing money pumps and thereby fails to be opportunistic. The single-souring money pump below is a purported example of this.
The agent’s preferences satisfy A≻A− and B⋈/A,A−. Suppose that it’s myopic and uses strong maximality at each node. The agent begins with A at node 0 (if we let ‘down’ be the default). It is permitted, though not compelled, to go ‘up’ at node 0 instead (since B will become available), but also to go ‘up’ upon arrival at node 1 (since A−⋈/B). Suppose it in fact goes ‘up’ at both node 0 and at node 1. This would leave it with A−, which is strictly worse than what it began with. This money pump is ‘non-forcing’ because the agent’s preferences are also consistent with avoiding it.
The agent need not be myopic, however. It can plan ahead.[9] To achieve opportunism for Suzumura consistent agents, I propose a choice rule which I’ll dub Dynamic Strong Maximality (DSM). DSM states that a plan p is permissible at node n just in case (a) it is strongly maximal at n and (b) no other such plan was previously more choiceworthy than p.
(Dynamic Strong Maximality) p∈D(Ω(T,n)) iff
(a) p∈CSM(Ω(T,n)) and
(b) ∄p∗∈CSM(Ω(T,n)):p∗∈CSM(Ω(T,n0))∌p .
DSM is a slight refinement of strong maximality. Condition (b) simply offers a partial tie-breaking rule whenever the agent faces multiple choiceworthy prospects. So, importantly, it never asks the agent to pick counter-preferentially. An agent following naive choice with DSM will, at each node, look ahead in the decision tree, select their favourite trajectory using DSM, and embark on it. It can continually re-evaluate its plans using naive-DSM as time progresses and, as the following result establishes, the agent will thereby never end up with something worse than what it began with.
Proposition 2 (Strong Dynamic Consistency Under Certainty via Naivety) Let T be an arbitrary tree where n is a choice node, n′∈N+(n), and p∈Ω(T,n) is consistent with S(n′). Then p(n)∈D(Ω(T,n)) iff p(n′)∈D(Ω(T,n′)). [Proof.]
Intuitively, this means that (i) if the agent now considers a trajectory acceptable, it will continue to do so as time passes, and (ii) if it at any future point considers some plan continuation acceptable, its past self would agree. It follows immediately that all and only the strongly maximal terminal nodes are reachable by agents choosing naively using DSM (derived as Corollary 1). This gives us opportunism: the agent will never pick a plan that’s strictly dominated some other available plan.
Under certainty, this result is unsurprising.[10] What is less obvious is whether this also holds under uncertainty. I will say that a Bayesian decision tree exhibits PIP-uncertainty just in case the probability of any given event does not depend on what the agent plans to do after the event has occurred. We can now state the next result.
Proposition 3 (Strong Dynamic Consistency Under PIP-Uncertainty via Naivety)
Let node n be non-terminal in decision tree T, n′∈N+(n), and plan p∈Ω(T,n) be consistent with S(n′). Assume Material Planning, Preference Stability, and Plan-Independent Probabilities. Then p∈D(Ω(T,n)) iff p∈D(Ω(T,n′)).
Proof. Lemma 3 establishes that p∈D(Ω(T,n)) implies p∈D(Ω(T,n′)). To prove the converse, suppose that p∈D(Ω(T,n′)). Node n was either a choice node or a natural node. If it was a choice node, then it follows immediately from Proposition 2 that p∈D(Ω(T,n)).
Now let n be a natural node. By Lemma 2, COpt(⋅)=CSM(⋅)=D(⋅) under coherent extension. So by Theorem 37 of Bradley (2017),
Vin′(p(n′))≥Vin′(p′(n′))∃i∈Z for all p′∈Ω(T,n′).
Let z′[q] denote the continuation selected by plan q upon reaching choice node n′. Thus
Vin′(z′[p])≥Vin′(z′[p′])∃i∈Z for all p′∈Ω(T,n′).
By Preference Stability,
Vin(z′[p])≥Vin(z′[p′])∃i∈Z for all p′∈Ω(T,n′). (1)
Notice that this implies that
Vin(z′[p])P(n′|n)≥Vin(z′[p′])P(n′|n)∃i∈Z for all p′∈Ω(T,n′). (2)
And by Plan-Independent Probabilities, this is equivalent to
Vin(z′[p])P(n′|p(n))≥Vin(z′[p′])P(n′|p′(n))∃i∈Z for all p′∈Ω(T,n′). (3)
By Material Planning, p∈CSM(Ω(T,n)) holds iff
∑jVin(zj[p])P(nj|p(n))≥∑jVin(zj[p′])P(nj|p′(n))∃i∈Z for all p′∈Ω(T,n′).
Using (2)-(3) this is equivalent to
Vin(z′[p])P(n′|n)+∑j≠j′Vin(zj[p])P(nj|n)≥Vin(z′[p′])P(n′|n)+∑j≠j′Vin(zj[p′])P(nj|n)
for some i∈Z and all p′∈Ω(T,n′). (4)
Formally, z′[p]=p(n′) omits description of p(nj) for all nj∈N+(n)∖{n′}. So, we can let p(nj)=p′(nj) at all remaining realisations nj. Then (4) reduces to
Vin(z′[p])P(n′|n)≥Vin(z′[p′])P(n′|n)
Vin(z′[p])≥Vin(z′[p′]). (The probability is nonzero as n′ is realised by assumption.)
This holds via (1), so p∈CSM(Ω(T,n)) and, by Lemma 2, p∈D(Ω(T,n)). ■
We have thereby shown that a naive DSM agent is strongly dynamically consistent in a very broad class of cases. Although these results are restricted to PIP-uncertainty, this applies to agents with complete preferences too. It’s just a result of the forward-looking nature of naive choice. In the next section, I will drop the PIP restriction by employing a different dynamic choice principle.
2.4. Sophisticated Choice
Sophistication is the standard principle in dynamic choice theory. It achieves dynamic consistency in standard cases by using backward induction to achieve the best feasible outcome. (This is also the method by which subgame perfect equilibria are found in dynamic games of perfect information.) However, backward induction is undefined whenever the prospects being compared are either incomparable or of equal value. Rabinowicz (1995) proposed a ‘splitting procedure’ to address this, and Asheim (1997) used a similar approach to refine subgame perfection in games.
According to this procedure, whenever there is a tie between multiple prospects, the agent will split the sequential decision problem into parts, where each part assumes that a particular prospect was chosen at that node. The agent then compares each part’s solution and picks its favourite as the solution to the grand decision problem. Intuitively, these agents will follow a plan as long as they lack “a positive reason for deviation” (Rabinowicz 1997). In other words, the agent will consider all the plans that would not make it locally act against their own preferences and, among those plans, proceed to pick the one with the best ex-ante outcome.
In the case of incomplete preferences, however, it turns out that strongly maximal sophisticated choice with splitting will not suffice to guarantee opportunism. The reason behind this is that strong maximality does not satisfy Set Expansion, and that backward induction makes local comparisons.[11]
Proposition 4 Strongly maximal sophisticated choice with splitting does not guarantee opportunism for Suzumura consistent agents. [Proof.]
DSM, however, will suffice.
Proposition 5 (Strong Dynamic Consistency Under Certainty via Sophistication)
Assume certainty and Suzumura consistency. Then DSM-based backward induction with splitting reaches a strongly maximal terminal node. [Proof.]
More importantly, we can guarantee this property under uncertainty even without PIP.
Proposition 6 (Strong Dynamic Consistency Under Uncertainty via Sophistication)
Let T be a Bayesian decision tree in which n is a non-terminal node, n′∈N+(n) is a successor, and p∈Ω(T,n) is consistent with S(n′). Assume Material Planning and Preference Stability. Then with DSM-based backward induction (DSM-BI), p is permissible at n iff p is permissible at n′.
Proof. We begin by formalising DSM-BI. For tree T, let X denote its terminal nodes, C its choice nodes, and N its natural nodes. Let I[n,A]={p∈Ω(T,n):p(n′)∈A} denote the set of plans available at n that are consistent with some associated plan continuation in A. We then define the tree’s permissible set of plans, Ψ(T), recursively:
The permissible set of plans is then given by Ψ(T)≜~Ψ(T,n0). Notice that this is the set of plans consistent with backward induction using DSM, and that splitting is implicit since each pruning of the decision tree is set-valued.
Now suppose that p∈~Ψ(T,n) for some n∈C.
Then p∈D(I[n,Φ(n)]) , where Φ(n)=⋃ni∈N+(n)~Ψ(T,ni).
So necessarily p∈I[n,Φ(n)]. By construction of I[⋅,Φ(⋅)], we know that p(n′)∈Φ(n).
And since Φ(n)=~Ψ(T,n′)∪⋃ni≠n′~Ψ(T,ni), we have p(n′)∈~Ψ(T,n′).
Next, suppose that p∈~Ψ(T,n) for some n∈N. Then p∈⋂ni∈N+(n)I[n,~Ψ(T,ni)] . So, for any particular n′∈N+(n), p∈I[n,~Ψ(T,n′)]. Therefore p(n′)∈~Ψ(T,n′) as needed.
Having established p∈~Ψ(T,n)⟹p(n′)∈~Ψ(T,n′), we proceed to the converse. (∗)
Notice that the only nodes reachable via sophisticated choice are those that are consistent with some plan p∈Ψ(T) which was initially permissible. Therefore, for any n′ that is reached, there must be some p∈Ω(T,n), consistent with n′ where n′∈N+(n), which satisfies p∈~Ψ(T,n).
Suppose p(n′)∈~Ψ(T,n′) for some reachable n′∈N. Whether n is a choice or a natural node, we know by construction of (2) and (3) that
~Ψ(T,n)⊆I[n,⋃ni∈N+(n)~Ψ(T,ni)].
Therefore, if n′ is reached, then the permissible plans at n′ must be continuations of plans that were permissible at n. Hence p(n)∈~Ψ(T,n).
Together with (∗), this establishes that p∈~Ψ(T,n) iff p(n′)∈~Ψ(T,n′). ■
This lets us achieve strong dynamic consistency even in cases where the probability of an event depends on what the agent plans to do after the event has occurred. An example of such a decision problem is Sequential Transparent Newcomb, as devised by Bryan Skyrms and Gerard Rothfus (cf Rothfus 2020b). So, even in this very general setting, our agent’s incomplete preferences aren’t hindering its opportunism.
2.5. Resolute Choice
A final canonical principle of dynamic choice is resoluteness as introduced by McClennen (1990). An informal version of this principle is often discussed in the AI alignment community under the name ‘updatelessness’. Briefly, a resolute agent will, first, pick its favourite trajectory now under the assumption that this plan will continue to be implemented as the agent moves through the decision tree. And, second, the agent will continually implement that plan, even if this makes it locally choose counter-preferentially at some future node.[12] It respects its ex-ante commitments.
Under certainty or uncertainty, this is the easiest principle with which to guarantee the invulnerability of agents with incomplete preferences (relative to those with complete preferences). By construction, the agent never implements a plan that was suboptimal from an earlier perspective. I will therefore omit formal derivations of dynamic consistency for resolute choosers.[13]
3. The Trammelling Concern
A possible objection to the relevance of the results above is what I’ll call the Trammelling Concern. According to this objection, agents with incomplete preferences who adopt DSM as a dynamic choice rule will, in certain sequential choice problems, or over the course of sufficiently many and varied ones, eventually converge in behaviour to an agent with complete preferences using Optimality as a choice rule. This would be worrying since complete preferences and optimal choice resembles the kind of consequentialism that precludes Thornley-style corrigibility.
This section aims to quell such worries. I begin with a taxonomy of our agent’s possible doxastic attitudes towards decision trees. First, the set of non-terminal nodes of a given tree will either contain only choice nodes, or it will contain some natural nodes. Second, the structure of a given tree will either be entirely known to the agent, or it will not. If it is not known, the agent will either have beliefs about all its possible structures, or its credence function will not be defined over some possible tree structures. We will refer to these three cases as certainty, uncertainty, and unawareness about structure, respectively.[14] Finally, at least under unawareness, the possible tree structures may or may not include terminal nodes (prospects) that are also present in the tree structure currently being considered by the agent. I will say the prospects are new if so and fixed if not.
This table summarises the situations our agent might find itself in and its cells indicate whether trammelling can occur in each case. This is based on the arguments and results below. The conclusions for (1)-(2) are based on conceptual considerations in section 3.1. Cases (3)-(4) are not discussed explicitly since uncertain tree structures can simply be represented as certain tree structures with natural nodes. The conclusions for (5) and (7) are based on formal results in section 3.2. For the sake of brevity, the effects of natural nodes under unawareness are left for later work.
3.1. Aware Choice
This section was co-authored with Eric Chen.
Let’s begin with an important distinction. As Bradley (2015) puts it, there’s a difference between "the choices that are permissible given the agent’s preferences, those that are mandatory and those that she actually makes" (p. 1). If an agent is indifferent between two options, for example, then it can be the case that (i) both are permissible, (ii) neither is mandatory, and (iii) a particular one is in fact chosen. One aspect of choice between incomparables that we need to preserve is that all were permissible ex-ante. The fact that one is in fact chosen, ex-post, is immaterial.
To see what this implies, consider first the case of certainty. Here we proved that DSM will result in only ex-ante strongly maximal plans being implemented (Proposition 2; Corollary 1; Proposition 5). Now consider the following toy case (Example 1). A Suzumura consistent agent can’t compare A and B. It’s offered a choice between the two. Suppose it chooses B. Does this constrain the agent to never pick A in future choices between A and B?
No. In fact, it’s a bit unclear what this would mean formally. Once we expand the decision tree to include future choices between A and B in some branches, everything boils down to the fact that all plans through this tree will result in either A or B. And so any plan will be permissible. What DSM constrains is which terminal nodes are reached; not how the agent gets there. Let’s see how far this reasoning can get us.
Example 2 A Suzumura consistent agent’s preferences satisfy A≻A− and B⋈/A,A−. It’s offered a choice between going ‘down’ for A or going ‘up’ to face a choice between A− and B. It happens to go ‘up’. Does this constrain the agent not to pick A− over B?
This is a case of an agent ending up on some trajectory that is only consistent with one of its coherent extensions ('completions'). One might worry that, at this point, we can treat the agent as its unique extension, and that this denies us any kind of corrigible behaviour. But there is a subtle error here. It is indeed the case that, once the agent has reached a node consistent with only one extension, we can predict how it will act going forward via its uniquely completed preferences. But this is not worrisome. To see why, let’s look at two possibilities: one where the agent is still moving through the tree, and another where it has arrived at a terminal node.
First, if it is still progressing through the tree, then it is merely moving towards the node it picked at the start, by a process we are happy with. In Example 2, option A− was never strongly maximal in comparison to A and B. We knew, even before the agent went ‘up’, that it wouldn’t pick A−. So the agent is no more trammelled once it has gone ‘up’ than it was at the beginning.
For a more concrete case, picture a hungry and thirsty mule. For whatever reason, this particular mule is unable to compare a bale of hay to a bucket of water. Each one is then placed five metres from the mule in different directions. Now, even if the mule picks arbitrarily, we will still be able to predict which option it will end up at once we see the direction in which the mule is walking. But this is clearly not problematic. We wanted the mule to pick its plan arbitrarily, and it did.
Second, if the agent has reached the end of the tree, can we predict how it would act when presented with a new tree? No; further decisions just constitute a continuation of the tree. And this is just the case we described above. If it did not expect the continuation, then we are simply dealing with a Bayesian tree with natural nodes. In the case of PIP-uncertainty, we saw that DSM will once again only result in the ex-ante strongly maximal plans being implemented (Proposition 3).[15] Here it's useful to recall that plans are formalised using conditionals:
p(n)=S(n)∧⋀|N+(n)|j=1[S(nj)→S(zj)], where nj∈N+(n) and zj∈N+(nj).
That is, plans specify what path to take at every contingency. The agent selects plans, not merely prospects, so no trammelling can occur that was not already baked into the initial choice of plans. The general observation is that, if many different plans are acceptable at the outset, DSM will permit the agent to follow through on any one of these; the ex-post behaviour will “look like” it strictly prefers one option, but this gets close to conflating what options are mandatory versus actually chosen. Ex-post behavioural trajectories do not uniquely determine the ex-ante permissibility of plans.
3.2. Unaware Choice
The conceptual argument above does not apply straightforwardly to the case of unawareness. The agent may not even have considered the possibility of a certain prospect that it ends up facing, so we cannot simply appeal to ex-ante permissibility. This section provides some results on trammelling in this context. But, first, given the argument about Bayesian decision trees under certain structure, one may ask: what, substantively, is the difference between the realisation of a natural node and awareness growth (if all else is equal)? Would the behaviour of our agent just coincide? I don't think so.
Example 3 Consider two cases. Again, preferences satisfy A≻A− and B⋈/A,A−.
Up top, we have a Bayesian tree. On the bottom, we have awareness growth, where each tree represents a different awareness context. In both, let’s suppose our agent went ‘up’ at node 0. In the Bayesian case, let’s also suppose the natural node (1) resolves such that the agent reaches node 2. In both diagrams, the agent ends up having to pick A− or B.
The permissible plans at the outset of the Bayesian tree are those that lead to A or to B (since A− is strictly dominated by A). But in the bottom case, it seems that our agent faces two distinct decision problems: one between A and B; one between A− and B. In the first problem, both options are permissible. And likewise in the second. So, the difference between these situations is that, in the latter case, our agent faces a new decision problem.
In the Bayesian case, our agent might end up at a future node in which the only available options are incomparable but nevertheless reliably picks one. But the reason for this is that another node, also available at the moment the agent picked its plan, was strictly preferred to one of these. The agent’s decision problem was between A, A−, and B. The arbitrary choice was between A and B. This is as it should be; there is no trammelling.
However, in the case of unawareness, the agent initially chose between A and B and now it must choose between A− and B. It never got to compare A to A− to B. It compared A to B and, separately, A− to B. Therefore, if it reliably picks B over A−, for the sake of opportunism, one could see this as a form of trammelling. I now turn to this issue.
For brevity, I will focus on cases 4 and 5 from the taxonomy above. In these worlds, all decision trees have choice nodes and terminal nodes, but they lack natural nodes. And our agent is unaware of some possible continuations of the tree they are facing. That is, it’s unaware of—places no credence on—the possibility that a terminal node is actually another choice node. But once it in fact gets to such a node, it will realise that it wasn’t terminal. There are then two ways this could play out: either the set of available prospects expands when the tree grows, or it doesn’t. Let’s consider these in turn. As we’ll see, the most salient case is under a certain form of expansion (section 3.2.3., Example 6).
3.2.1. Fixed Prospects (No Trammelling)
Here I’ll show that when prospects are fixed, opportunism and non-trammelling are preserved. We begin with an illustrative example.
Example 4 The agent’s preferences still satisfy A≻A− and B⋈/A,A−.
The agent initially sees the top tree. DSM lets it pick A or B, arbitrarily. Suppose it in fact goes for A. Then its awareness grows and the tree now looks like the bottom one. It can stay put (go ‘down’ to A) or move ‘up’ and choose between B and A−. DSM still says to pick, arbitrarily, any path leading to A or to B. Suppose it goes for B. There—no trammelling.
Here’s the lesson. Our agent will embark on a path that’ll lead to a node that is DSM with respect to the initial tree. When its awareness grows, that option will remain available in the new tree. By Set Contraction (Lemma 4) this option will also remain DSM in the new tree. So, picking it will still satisfy opportunism. And regarding trammelling, it can still pick entirely arbitrarily between all initially-DSM nodes. DSM constrains which prospects are reached; not how to get there. We can state this as follows.
Proposition 7 Assume no natural nodes. Then, DSM-based choice under awareness growth will remain arbitrary whenever the set of available prospects is fixed. [Proof.]
3.2.2. New Prospects (No Trammelling)
Now consider the case where the set of available prospects expands with the tree. It's of course possible that our agent gets to a terminal node that isn’t strongly maximal according to the new tree. This could happen if they get to an initially-acceptable terminal node and then realise that a now-inaccessible branch would let them access a prospect that’s strictly preferred to all those in the initial tree.[16] But, importantly, this applies to agents with complete preferences too. It’s simply an unfortunate feature of the environment and the agent’s epistemic state. Complete preferences don’t help here.
But there is a class of cases in which completeness, at first glance, seems to help.
Example 5 The agent’s preferences satisfy A≻A−∼B and A⋈/B (unlike before).
The agent sees the tree on the left. DSM lets it pick A or B, arbitrarily. Suppose it in fact goes for B. Now its awareness grows and the tree looks like the one on the right. It can stay put (go ‘down’ to B) or move ‘up’ to get A−.
Now, none of the available options are DSM in the full tree, but the agent still has to pick one. This, on its own, is not problematic since it could just be an unfortunate aspect of the situation (as dismissed above). But in this particular case, because an agent with complete preferences would satisfy transitivity, it would never go for B in the first place. This kind of issue wouldn’t occur if our agent’s incomplete preferences were transitive, rather than just strongly acyclic.
So let’s impose transitivity. Then our agent wouldn’t pick B in the first place. In general it will now remain opportunistic in the same way that its complete counterparts are. That’s because it would never initially choose arbitrarily between options that all its coherent extensions have a strict preference between. So it would never pick in a way that makes it realise that it made a foreseeable mistake once more options come into view. To operationalise this, I'll say that an agent facing deterministic decision trees fails to be opportunistic under awareness growth iff
This agent is opportunistic otherwise.[17] We can now state the associated result.
Proposition 8 Assume transitive preferences and no natural nodes. Then, under all possible forms of awareness growth, naive choice via DSM is opportunistic. [Proof.]
That gives us opportunism, but what about non-trammelling? Will our agent ever have to pick one option over another despite them being incomparable? Yes, in some cases.
3.2.2. New Prospects (Bounded Trammelling)
Example 6 The agent’s preferences satisfy A≻A− and B⋈/A,A−.
It faces the same trees as in the previous example. DSM first lets it pick A or B, arbitrarily. Suppose it goes for B. Now its awareness grows and the tree looks like the one on the right. It can stay put (go ‘down’ to B) or move ‘up’ to get A−. Since only B is DSM in the global tree, our agent might reliably pick B over A−, despite them being incomparable. Trammelled.
This is a special property of unawareness. Thankfully, however, we can bound the degree of trammelling. And I claim that this can be done in a rather satisfying way. To do this, let’s formally define an extension of DSM that will give us opportunism under awareness growth. Let T1 denote the initial tree, with initial node n0, and T2 the tree available after awareness growth, with initial node n0. And let T denote the appending of T2 on T1.
(Global-DSM) p∈G(Ω(T2,n0)) iff
(i) p∈CSM(Ω(T2,n0)) and
(ii) ∄p∗∈CSM(Ω(T2,n0)):p∗∈CSM(Ω(T,n0))∌p.
Notice that G-DSM doesn’t look at what happens at other previously-terminal nodes after awareness grows. These are unreachable and would leave the choice rule undefined in some cases. (This holds with complete preferences too.) This rule naturally extends opportunism to these cases; it says to never pick something if you knew that you could’ve had something better before. We can now state some results.
Proposition 9 (Non-Trammelling I) Assume transitive preferences and no natural nodes. Then, under all possible forms of awareness growth, globally-DSM naive choice will remain arbitrary whenever the available prospects are (i) mutually incomparable and (ii) not strictly dominated by any prospect. [Proof.]
That gives us a sufficient condition for arbitrary choice. To find out how often this will be satisfied, we define ‘comparability classes’ as subsets of prospects within which all are comparable and between which none are. A comparability-based partitioning of the prospects is possible when comparability is transitive.[18] The following results then follow.
Proposition 10 (Bounded Trammelling I) Assume that comparability and preference are transitive and that there are no natural nodes. Then, under all possible forms of awareness growth, there are at least as many prospects between which globally-DSM naive choice is guaranteed to be arbitrary as there are comparability classes.
Proof. We first partition the (possibly uncountable) set of prospects X into (possibly uncountable) subsets of (possibly uncountable) mutually comparable prospects.
Given transitivity, ⋈ is an equivalence relation on X. Then, for any x∈X, we construct an equivalence class: [x]⋈≜{y∈X:y⋈x}. Call this set the comparability class of x.
This lets {[x]⋈}x∈X form a partition of X.
We identify the class-optimal prospects as follows: X∗≜⋃x∈XCOpt([x]⋈).
Let Ω(T2,n0)⊆X∗. Suppose, for contradiction, that G(Ω(T2,n0))≠Ω(T2,n0).
Since G is a choice function, G(A)⊆A for any set A. Then G(Ω(T2,n0))⊂Ω(T2,n0).
Then, by G-DSM, there exists some p∈Ω(T2,n0) such that
(i’) p∉CSM(Ω(T2,n0)) or
(ii’) ∃p∗∈CSM(Ω(T2,n0)):p∗∈CSM(Ω(T,n0))∌p.
Given transitivity, and since all elements of Ω(T2,n0) are mutually incomparable or indifferent, condition (i’) does not hold. Therefore p∉CSM(Ω(T,n0)).
By transitivity, this implies that p′≻p for some p′∈Ω(T,n0). (1)
But since p∈COpt([x]⋈) for some x∈X, we know that p∈CSM(X). (2)
By Set Contraction, Ω(T,n0)⊆X contradicts (1)-(2).
This establishes that G(Ω(T2,n0))=Ω(T2,n0) whenever Ω(T2,n0)⊆X∗.
The set of all prospects satisfying this is of size |X∗|≥|{[x]⋈}x∈X|, as needed. ■
Corollary 2 (Bounded Trammelling II) Assume that comparability and preference are transitive and that there are no natural nodes. Then, whenever k class-optimal prospects are available, choice will be arbitrary between at least k prospects. [Proof.]
3.3. Discussion
It seems we can’t guarantee non-trammelling in general and between all prospects. But we don’t need to guarantee this for all prospects to guarantee it for some, even under awareness growth. Indeed, as we’ve now shown, there are always prospects with respect to which the agent never gets trammelled, no matter how many choices it faces. In fact, whenever the tree expansion does not bring about new prospects, trammelling will never occur (Proposition 7). And even when it does, trammelling is bounded above by the number of comparability classes (Proposition 10).
And it’s intuitive why this would be: we’re simply picking out the best prospects in each class. For instance, suppose prospects were representable as pairs ⟨s,c⟩ that are comparable iff the s-values are the same, and then preferred to the extent that c is large. Then here’s the process: for each value of s, identify the options that maximise c. Put all of these in a set. Then choice between any options in that set will always remain arbitrary; never trammelled.
Three caveats are worth noting. First, sceptical readers may not agree with our initial treatment of (non-)trammelling under aware choice (i.e., known tree structures, section 3.1.). That section is based on a conceptual argument rather than formal results, so it should be evaluated accordingly. However, at least some of the results from the section on unawareness could be used to dampen many reasonable worries here. Whenever non-trammelling is satisfied under awareness growth with Global-DSM, it will likewise be satisfied, mutatis mutandis, by DSM when the tree structure is known.
Second, we've only considered part of the taxonomy described above. Due to time constraints, we left out discussion of unaware choice in trees with natural nodes. We suspect that extending the analysis to these kinds of cases would not meaningfully affect the main conclusions, but we hope to look into this in later work. Finally, we haven't provided a full characterisation of choice under unawareness. The literature hasn't satisfactorily achieved this even in the case of complete preferences, so this falls outside the scope of this article.
Conclusion
With the right choice rule, we can guarantee the invulnerability—unexploitability and opportunism—of agents with incomplete preferences. I’ve proposed one such rule, Dynamic Strong Maximality, which nevertheless doesn’t ask agents to pick against their preferences. What’s more, the choice behaviour this rule induces is not representable as the agent having implicitly completed its preferences. Even under awareness growth, the extent to which the rule can effectively complete an agent’s implied preferences is permanently bounded above. And with the framework provided, it’s possible to make statements about which kinds of completions are possible, and in what cases.
This article aims to be somewhat self-contained. In future work, I’ll more concretely consider the implications of this for Thornley’s Incomplete Preference Proposal. In general, however, I claim that worries about whether a competent agent with preferential gaps would in practice (partially) complete its preferences need to engage with the particulars of the situation: the preference structure, the available decision trees, and so on. Full completion won't occur, so the relevant question is whether preferential gaps will disappear in a way that matters.
References
Asheim, Geir. 1997. “Individual and Collective Time-Consistency.” The Review of Economic Studies 64, no. 3: 427–43.
Bales, Adam. 2023. “Will AI avoid exploitation? Artificial general intelligence and expected utility theory.” Philosophical Studies.
Bossert, Walter and Kotaro Suzumura. 2010. “Consistency, Choice, and Rationality.” Harvard University Press.
Bradley, Richard and Mareile Drechsler. 2014. “Types of Uncertainty.” Erkenntnis 79, no. 6: 1225–48.
Bradley, Richard. 2015. “A Note on Incompleteness, Transitivity and Suzumura Consistency.” In: Binder, C., Codognato, G., Teschl, M., Xu, Y. (eds) Individual and Collective Choice and Social Welfare. Studies in Choice and Welfare. Springer, Berlin, Heidelberg.
Bradley, Richard. 2017. Decision Theory with a Human Face. Cambridge: Cambridge University Press.
Gustafsson, Johan. 2022. Money-Pump Arguments. Elements in Decision Theory and Philosophy. Cambridge: Cambridge University Press.
Hammond, Peter J. 1988. “Consequentialist foundations for expected utility.” Theory and Decision 25, 25–78.
Huttegger, Simon and Gerard Rothfus. 2021. “Bradley Conditionals and Dynamic Choice.” Synthese 199 (3-4): 6585-6599.
Laibson, David and Yeeat Yariv. 2007. "Safety in Markets: An Impossibility Theorem for Dutch Books." Working Paper, Department of Economics, Harvard University.
McClennen, Edward. 1990. Rationality and Dynamic Choice: Foundational Explorations. Cambridge: Cambridge University Press.
Rabinowicz, Wlodek. 1995. “To Have One’s Cake and Eat It, Too: Sequential Choice and Expected-Utility Violations.” The Journal of Philosophy 92, no. 11: 586–620.
Rabinowicz, Wlodek. 1997. “On Seidenfeld‘s Criticism of Sophisticated Violations of the Independence Axiom.” Theory and Decision 43, 279–292.
Rothfus, Gerard. 2020a. “The Logic of Planning.” Doctoral dissertation, University of California, Irvine.
Rothfus, Gerard. 2020b. “Dynamic consistency in the logic of decision.” Philosophical Studies 177:3923–3934.
Suzumura, Kotaro. 1976. “Remarks on the Theory of Collective Choice.” Economica 43: 381-390.
Thornley, Elliott. 2023. “The Shutdown Problem: Two Theorems, Incomplete Preferences as a Solution.” AI Alignment Awards
Appendix: Proofs
Proposition 1 Suzumura consistent agents myopically applying strong maximality are unexploitable under certainty.
Proof. By myopic strong maximality, whenever an agent is presented with a set of alternatives containing a prospect strictly preferred to all others, it is chosen. Suppose such a Suzumura consistent agent were forcibly money pumped: beginning with some α1 and ending with a strictly dispreferred α1−ϵ, with each choice resulting from a strict preference. Then there must be a set of prospects satisfying α1≺α2≺...≺αn−1≺αn where αn=α1−ϵ. This trivially implies that α1⪯α2⪯...⪯αn−1⪯α1−ϵ. By Strong Acyclicity, we have α1⊁α1−ϵ, a contradiction. ■
Lemma 1 (Dynamic Consistency Under Certainty via Naivety) Let T be an arbitrary tree where n is a choice node, n′∈N+(n), and p∈Ω(T,n) is consistent with S(n′). Then p(n)∈D(Ω(T,n)) implies p(n′)∈D(Ω(T,n′)) .
Proof. There are no natural nodes, so for any nodes m and m′ consistent with plan x, we have x(m)=x(m′). Therefore, by DSM, p(n)∈D(Ω(T,n)) is equivalent to
p(n′)∈CSM(Ω(T,n)) and
∄p∗∈CSM(Ω(T,n)):p∗∈CSM(Ω(T,n0))∌p(n′).
Noting that Ω(T,n′)⊆Ω(T,n) and that Strong Maximality satisfies Set Contraction (Bradley 2015), we know p(n′)∈CSM(Ω(T,n))⟹p(n′)∈CSM(Ω(T,n′)). So
p(n′)∈CSM(Ω(T,n′)). (1)
Any plan unavailable at n is also unavailable at n′, which implies that
∄p∗∈CSM(Ω(T,n′)):p∗∈CSM(Ω(T,n0))∌p(n′). (2)
By DSM, (1)-(2) is equivalent to p(n′)∈D(Ω(T,n′)). ■
Proposition 2 (Strong Dynamic Consistency Under Certainty via Naivety) Let T be an arbitrary tree where n is a choice node, n′∈N+(n), and p∈Ω(T,n) is consistent with S(n′). Then p(n)∈D(Ω(T,n)) iff p(n′)∈D(Ω(T,n′)).
Proof. There are no natural nodes, so for any nodes m and m′ consistent with plan x, x(m)=x(m′). Suppose that p(n′)∈D(Ω(T,n′)) while p(n)∉D(Ω(T,n)).
Suppose p(n)∉CSM(Ω(T,n)). Then by Set Contraction, p(n)∉CSM(Ω(T,n′)). And since there are no natural nodes, p(n)=p(n′). Hence p(n′)∉D(Ω(T,n′)), a contradiction.
Suppose p(n)∈CSM(Ω(T,n)). By Theorem 2 of Bradley (2015), Strong Maximality is decisive. Therefore, there must be another plan p∗∈CSM(Ω(T,n)) that was initially more choiceworthy; that is, p∗∈CSM(Ω(T,n0))∌p(n). Again, p(n)=p(n′). This shows that p(n′)∉CSM(Ω(T,n0)). Hence p(n′)∉D(Ω(T,n′)), a contradiction.
We have a contradiction, so p(n′)∈D(Ω(T,n′))⟹p(n)∈D(Ω(T,n)) . Using Lemma 1, we have thereby shown that p(n)∈D(Ω(T,n)) iff p(n′)∈D(Ω(T,n′)). ■
Corollary 1 Under certainty, all and only strongly maximal terminal prospects are reachable by naive DSM.
Proof. Recall that, under certainty, a plan can be identified by the conjunction of propositions describing the information state at each node of its continuation. A node always logically entails its preceding nodes, so a plan under certainty can simply be identified by its unique terminal node. Let X denote the set of propositions at the terminal nodes.
We can thereby establish, for part (a) of DSM, that CSM(Ω(T,n0))=CSM(X). Part (b) follows trivially at the initial node n0, so D(Ω(T,n0))=CSM(X). Proposition 2 establishes that under certainty, a plan is DSM iff its immediate continuation is DSM. By induction on continuation-consistent nodes, all Strongly Maximal terminal prospects are reachable by DSM. And since D(Ω(T,n))⊆D(Ω(T,n0))=CSM(X) for all nodes n that are consistent with a plan p∈D(Ω(T,n0)), we know that DSM reaches only Strongly Maximal terminal prospects. ■
Lemma 2 Under certainty and the coherent extension of a (Strongly Acyclic) preference relation, Dynamic Strong Maximality reduces to Optimality.
Proof. By Theorem 1 of Bradley (2015), when a Strongly Acyclic preference relation is completed, Strong Maximality coincides with Optimality. DSM becomes equivalent to: p∈D(Ω(T,n)) iff
(a’) Plan p is Optimal at n. That is, p(n)⪰p′(n)∀p′∈Ω(T,n).
(b’) No Optimal plan was previously better: ∄p∗∈COpt(Ω(T,n)):p∗(n0)≻p(n0).
Let p,p′∈COpt(Ω(T,n)) and suppose that p′∈COpt(Ω(T,n0)). Then, because we have Ω(T,n)⊆Ω(T,n0), the Set Expansion property of Optimality implies p∈COpt(Ω(T,n0)), i.e., that p(n0)∼p′(n0). These n-Optimal plans were chosen arbitrarily, so this suffices to show that ∄p∗∈COpt(Ω(T,n)):p∗(n0)≻p(n0). Hence (b’) follows from (a’) under certainty. ■
Lemma 3 (Dynamic Consistency Under PIP-Uncertainty via Naivety) Let n be a non-terminal node in Bayesain decision tree T, n′∈N+(n), and plan p∈Ω(T,n) be consistent with S(n′). Assume Material Planning, Preference Stability, and Plan-Independent Probabilities. Then p∈D(Ω(T,n)) implies p∈D(Ω(T,n′)) .
Proof. Suppose that p∈D(Ω(T,n)). Node n is either a choice node or a natural node. If it is a choice node, then it follows immediately from Lemma 1 that p∈D(Ω(T,n′)). Now let n be a natural node.
Then by DSM, p∈CSM(Ω(T,n)). By Lemma 2, COpt(⋅)=CSM(⋅)=D(⋅) under coherent extension. Therefore, by Theorem 37 of Bradley (2017),
Vin(p)≥Vin(p′)∃i∈Z for all p′∈Ω(T,n). (1)
Suppose, for contradiction, that p∉D(Ω(T,n′)) for some n′∈N+(n). This implies that
¬[∀p′∈Ω(T,n′),∃i∈Z:Vin′(p(n′))≥Vin′(p′(n′))], i.e., that
∃p′∈Ω(T,n′):∀i∈Z,Vin′(p(n′))<Vin′(p′(n′)) .
Let z′[p∗] denote the continuation selected by plan p∗ upon reaching choice node n′.
Then we can re-write the above as Vin′(z′[p])<Vin′(z′[p′])∀i∈Z.
And by Preference Stability, Vin(z′[p])<Vin(z′[p′])∀i∈Z. (2)
By applying Material Planning to (1), we get, for all p′∈Ω(T,n),
∑jVin(zj[p])P(nj|p(n))≥∑jVin(zj[p′])P(nj|p′(n))∃i∈Z
and, by assuming Plan-Independent Probabilities,
∑jVin(zj[p])P(nj|n)≥∑jVin(zj[p′])P(nj|n)∃i∈Z. (3)
Let Z′ denote the set of completions according to which (3) holds.
Then Vn(zj[p])≥Vn(zj[p′])∀i∈Z′ for all j∈N|N+(n)|. That is because, if this failed to hold for any j, then plan p could be altered such that zj[p]=zj[p′]. But such Pareto improvements are unavailable since p is DSM at node n.
In particular, Vn(z′[p])≥Vn(z′[p′])∀i∈Z′ as z′∈{z1,...}. But since Z′⊆Z, condition (2) implies that Vin(z′[p])<Vin(z′[p′])∀i∈Z′, a contradiction. ■
Proposition 4 Strongly maximal sophisticated choice with splitting does not guarantee opportunism for Suzumura consistent agents.
Proof. The proof is by counterexample. Consider a Suzumura consistent agent facing the following simple decision tree with preferences satisfying x≻y≻z and x⋈/z.
Proceeding via backward induction, the only permissible choice at node 1 is x. The agent then compares x and z at node 0. These are incomparable so the agent splits the problem and gets two partial solutions: x and z. The strongly maximal solutions are CSM({x,z})={x,z}. Although x is indeed permissible, the agent could incidentally end up with z despite having been able to reach y, a strictly preferred alternative. ■
Remark. Decision trees lack a natural assignment of the ‘default’ outcome; i.e., what the agent ‘starts out with’. In this case we can think of the agent as starting with z, and choosing whether to engage with a decision problem by going ‘up’ at node 0. Then we can claim that it is permissible, according to strongly maximal sophistication with splitting, for the agent to stay put at a strictly dispreferred node. The agent is therefore not opportunistic. It is worth noting that y is also impermissible according to planning-DSM as described above. The only permissible plans under DSM are CSM({x,y,z})={x}. But since x dominates y, a DSM agent is nevertheless opportunistic: it could not even incidentally pick a strictly dominated prospect.
Lemma 4 DSM satisfies Set Contraction.
Proof. Recall Set Contraction: if α∈C(B) and α∈A⊆B then α∈C(A). Now let A,B be sets of plans in tree T. Suppose that α∈D(B) and α∈A⊆B. Then by DSM, α∈CSM(B). By Theorem 3 of Bradley (2015), CSM(⋅) satisfies Set Contraction, so
α∈CSM(A). (1)
By DSM, ∄α∗∈B:α∗∈CSM(Ω(T,n0))∌α. And since A⊆B, we also know that
∄α∗∈A:α∗∈CSM(Ω(T,n0))∌α. (2)
By DSM, (1)-(2) is equivalent to α∈D(A). ■
Proposition 5 (Strong Dynamic Consistency Under Certainty via Sophistication) Assume certainty and Suzumura consistency. Then DSM-based backward induction with splitting (DSM-BIS) reaches a strongly maximal terminal node.
Proof. We first establish that every strongly maximal terminal node is preserved under some split of DSM-BIS. Let X denote the terminal nodes of a tree and denote by m the number of final choice nodes. For any such node ni, its associated terminal nodes are N+(ni)⊆X. By Set Contraction, we know that for any x∈CSM(X):x∈N+(ni) we have x∈D(N+(ni)). And since ⋃iN+(ni)=X, this more generally implies that
∀x∈CSM(X),∃i∈Nm:x∈D(N+(ni)). (1)
Let ri=|D(N+(ni))|. Whenever ri>1 for some i∈Nm, the splitting procedure will induce at least ri separate trees. Each will initially preserve one element of the DSM set of terminal nodes following ni. We therefore know from (1) that, for any x∈CSM(X), there is some split which will initially preserve x. The splitting procedure is repeatedly nested, as needed, within each subtree created via DSM-BIS elimination, so by Set Contraction (Lemma 4), this likewise applies to all subsequent subtrees. With Nj+(⋅) denoting possible continuations under split j, we can now claim that
∀x∈CSM(X),∃j∈Nk:x∈D(Nj+(n0)).
Let Sj denote the partial solutions under split j. Then since Sj=D(Nj+(n0)), this establishes that ∀x∈CSM(X),∃j∈Nk:x∈Sj. And letting S=⋃jSj, we can state
∀x∈CSM(X),x∈S, i.e. CSM(X)⊆S. (2)
Because we also have S⊆X, Set Contraction implies that
CSM(X)⊆CSM(S). (3)
DSM-BIS then selects among D(S). Since D(⋅)⊆CSM(⋅), we know from (2) that
∀x∈D(X),x∈S.
So by Set Contraction, ∀x∈D(X),x∈D(S). Clearly, D(X)=CSM(X) since X are all the terminal nodes. Therefore ∀x∈CSM(X),x∈D(S). This establishes that
CSM(X)⊆D(S), (4)
i.e., that all strongly maximal terminal nodes are DSM at S. To show the other direction, suppose for contradiction that ∃x′∈D(S):x′∉CSM(X).
Since x′ is not a strongly maximal terminal node, we know by the decisiveness of strong maximality that ∃x∗∈X∖{x′}:x∗∈CSM(X). By (3)-(4), this x∗ must be a member of both CSM(S) and D(S)=CSM(X). So by condition (b) of DSM, x′∉D(S), a contradiction.
Therefore CSM(X)⊇D(S), which with (4) implies that D(S)=CSM(X). ■
Proposition 7 Assume no natural nodes. Then, DSM-based choice under awareness growth will remain arbitrary whenever the set of available prospects is fixed.
Proof. Let Ω(T1,n0) denote the initially available prospects. Upon reaching n0 the agent’s awareness grows and it faces Ω(T2,n0) . Suppose Ω(T2,n0)⊆Ω(T1,n0) .
By Set Contraction, CSM(Ω(T2,n0))⊆CSM(Ω(T1,n0)).
Choice was arbitrary within CSM(Ω(T1,n0)), and will be arbitrary in CSM(Ω(T2,n0)).
Therefore, we know that for any x,y∈Ω(T1,n0) between which choice was arbitrary, choice will remain arbitrary between x and y whenever x,y∈Ω(T2,n0). ■
Proposition 8 Assume transitive preferences and no natural nodes. Then, under all possible forms of awareness growth, naive choice via G-DSM is opportunistic.
Proof. Let X denote the set of all prospects over which the agent’s preference relation is defined (i.e., candidates for terminal nodes). Let X1 denote the terminal nodes reachable in the initial tree T1; X2 the terminal nodes reachable (once awareness grows) in the new tree T2 at the previously chosen node n0; and XG the set of all terminal nodes (reachable or not) in the grand tree TG.
Since there are no natural nodes, X1=Ω(T1,n0) and X2=Ω(T2,n0)=Ω(T,n0) according to the agent’s doxastic state at those nodes. By Theorem 1 of Bradley (2015) strong maximality and maximality coincide under transitivity. We can therefore use maximality going forward.
Node n0 is, by construction, chosen via DSM in T1. Therefore, by Proposition 2, DSM guarantees that p(n0)∈CMax(Ω(T1,n0)) for any p∈Ω(T1,n0) consistent with S(n0).
(Note: with some abuse of notation, I will apply choice functions and preference relations to terminal nodes. This should be interpreted as attitudes towards their associated prospects.)
Awareness then grows and the agent faces T2. Consider two cases.
Case 1: (X1∪X2)∩CMax(XG)=∅. Here the best nodes are not the initially terminal nodes (nor are they accessible after reaching n0). Therefore, no strongly maximal prospect in the grand tree was available in the initial tree. So, opportunism is satisfied automatically.
Case 2: (X1∪X2)∩CMax(XG)≠∅. This is the situation in which the best nodes are either in the initial tree or the new tree. Notice that XG=X1∪X2∪X3 for some set X3 (the now-inaccessible new terminal nodes). Sub-cases:
If X1∩CMax(XG)≠∅, then by Set Expansion, n0∈CMax(XG). And so for any x∈XG, x⊁n0. Since n0∈X2, by Set Contraction, n0∈CMax(X2). For any y∈CMax(X2), y⊀n0. So, for all y∈CMax(X2), x⊁y for any x∈XG. Whatever is in fact chosen after awareness growth, it will not be strictly dominated by anything in the grand tree.
If X1∩CMax(XG)=∅, then necessarily X2∩CMax(XG)≠∅. Then for some x∈CMax(XG), x∈X2. By Set Contraction, x∈CMax(X2) for all such x. Hence CMax(X2)∩CMax(XG)≠∅.
Since ∃x∈CMax(X2)∩CMax(XG), by transitivity, we know that for any y∈CMax(XG) and z∈CMax(X2), y⊁z. So, whatever is in fact chosen after awareness growth, it will not be strictly dominated by anything in the grand tree.
Therefore, CMax(X2)⊆CMax(XG) . So only maximal prospects in the grand tree are reached. ■
Proposition 9 (Non-Trammelling I) Assume transitive preferences and no natural nodes. Then, under all possible forms of awareness growth, globally-DSM choice will remain arbitrary whenever the available prospects are (i) mutually incomparable and (ii) not strictly dominated by any prospect.
Proof. Let X denote the set of all prospects over which the agent’s preference relation is defined (i.e., candidates for terminal nodes). Our agent reaches node n0, its awareness grows, and faces mutually incomparable prospects Ω(T2,n0)⊆X (there are no natural nodes). Necessarily, then, CSM(Ω(T2,n0))=Ω(T2,n0).
Suppose, also, that these are not strictly dominated: ∀p∈Ω(T2,n0),∄q∈X:q≻p . (∗)
Then given transitivity, Ω(T2,n0)⊆CSM(X). Before awareness growth, the available prospects were Ω(T1,n0)⊆X.
For globally-DSM choice between incomparables to be non-arbitrary, it must be the case that G(Ω(T2,n0))⊂CSM(Ω(T2,n0)), i.e., that some prospects in Ω(T2,n0) are more choiceworthy than others at the grand tree T’s initial node n0. Since there are no natural nodes, this is equivalent to saying that
p∈CSM(Ω(T,n0))∌p′ for some p,p′∈Ω(T2,n0).
Given transitivity, this implies that ∃q∈Ω(T,n0):q≻p′. Since Ω(T,n0)⊆X, this contradicts (∗). ■
Corollary 2 (Bounded Trammelling II) Assume that comparability and preference are transitive and that there are no natural nodes. Then, whenever k class-optimal prospects are available, choice will be arbitrary between at least k prospects.
Proof. Given transitivity, [x]⋈≜{y∈X:y⋈x} is an equivalence class.
We first show that CMax(X)=⋃x∈XCOpt([x]⋈).
Suppose a∈CMax(X). Then ∄b∈X:b≻a. Hence ∄c∈[a]⋈:c≻a. Given that all elements in a class are comparable, a⪰b∀b∈[a]⋈, i.e., a∈COpt([a]⋈). Therefore a∈⋃x∈XCOpt([x]⋈), establishing CMax(X)⊆⋃x∈XCOpt([x]⋈).
Suppose a∈⋃x∈XCOpt([x]⋈). Then since ether [x]⋈=[y]⋈ or [x]⋈∩[y]⋈=∅ for all x,y∈X, we know a∈COpt([a]⋈). Hence ∀b∈X:b⋈a,a⪰b. This implies b⊁a.
And ∀c∈X:c⋈/a,c⊁a. Therefore ∀x∈X,x⊁a meaning a∈CMax(X).
So ⋃x∈XCOpt([x]⋈)⊆CMax(X) . This establishes that the maximal set and the class-optimal prospects coincide.
Next, suppose A⊆CMax(X) and A⊆Ω(T,n) at some node n in deterministic tree T.
Let k=|A| and suppose, for contradiction, that choice at n is arbitrary between fewer than k prospects. Then |G(Ω(T,n))|<k.
Under preference transitivity, this implies that ∃a∈A,∃b∈Ω(T,n):b≻a. (∗)
But since a∈CMax(X) for all a∈A, and Ω(T,n)⊆X, Set Contraction implies that a∈CMax(Ω(T,n)). Hence ∄b∈Ω(T,n):b≻a, contradicting (∗). ■
Nate Soares has also remarked, regarding Thornley’s proposal, that the consequences of violating the von Neumann-Morgenstern (vNM) axioms should be explored. This is one such exploration.
Though I will note that, in any case, the vNM axiomatisation is plausibly not the relevant baseline here. Instead it’d be the subjective representation theorems from Savage, Bolker-Jeffrey, Joyce, etc. And as we’ll see below, the Jeffrey framework has been usefully extended to the case of incompleteness.
Though see Bales (2023) and Laibson & Yariv (2007) for reasons to be sceptical of unqualified versions of this claim.
Opportunism implies unexploitability, so invulnerability is in fact equivalent to opportunism.
I will often refer to various properties of choice functions. For those unfamiliar with these, I suggest Richard Bradley’s introductory text on decision theory, section 4.2.
Notation:
⪰ (weak preference) is a reflexive binary relation on a set of prospects.
∼ (indifference) is the symmetric part of ⪰.
≻ (strict preference) is the anti-symmetric part of ⪰.
⋈ (comparability) is a relation satisfying α⋈β iff α⪰β or β⪰α.
A slash through a relation denotes its negation (e.g., α⋈/β iff α and β are incomparable).
C(⋅) is decisive iff C(X) is always nonempty (when X is nonempty).
The conditional ‘→’ is operationalised below in Definition 3. It will differ from the Bradley conditional used in Huttegger and Rothfus (2021).
Explaining the conditions:
Non-triviality: ∃α∈Ω:α⪰⊤, where ⊤ is the tautology.
⪰ has a minimal coherent extension, ⪰′, on Ω iff (i) α⪰β⟹α⪰′β, (ii) α≻β⟹α≻′β, and (iii) ⪰′ is complete and transitive. Indeed, ⪰ is strongly acyclic by Theorem 2 of Bradley (2015).
Impartiality: Suppose α∼β and for some γ≁α such that αγ=⊥=βγ, we have (α∨γ)∼(β∨γ). Then for all such γ, (α∨γ)∼(β∨γ).
Continuity: Let {α1,α2,...} be a countable set such that α1⊨α2⊨.... Suppose β⪰αi and αi⪰γ for all i. Then β⪰⋃i{αi} and ⋃i{αi}⪰γ.
A desirability measure V satisfies V(⊤)=0 (Normality) and ∀α,β∈Ω∖{⊥}:α∧β=⊥,α⪰β⟺α⪰(α∨β)⪰β (Averaging).
In section 3.2. I consider issues related to what happens if it can only plan ahead to a limited extent (or not at all).
Note that the notion of ‘certainty’ used here rules out Sequential Transparent Newcomb (Rothfus 2020b) with a perfect predictor. The results in section 2.4. do not.
C(⋅) satisfies Set Expansion iff whenever B⊆A∋α, then α,β∈C(B) and β∈C(A) implies α∈C(A).
According to Gauthier's (1997) framing.
Note that, below, I will consider the case of unawareness. For discussion of resolute choice under awareness growth, I’ll refer to Macé et al (2023).
The latter is sometimes known as state space uncertainty; see Bradley and Drechsler (2014).
In the general case of uncertainty, the agent is able to only implement the strongly maximal feasible plans (Proposition 6).
Here’s an example. Suppose the agent can choose between going ‘up’ and ‘down’. If it goes ‘up’, it gets A. If it goes ‘down’, it gets to choose between A+ and B. (This is the structure of a single-sweetening money pump.) If the agent is aware of the tree structure, then naive DSM choice lets it go for either ‘down-A+’ or ‘down-B’.
If the agent is unaware and thinks that ‘down’ leads to B only, then naive DSM choice lets it initially go ‘up’ (A) or ‘down’ (B). If it goes ‘down’, it can pick arbitrarily and opportunistically between A+ and B once its awareness grows. But if it goes ‘up’ it will realise, after awareness growth, that it could’ve done better. The problem in the latter case, however, is centrally a result of unawareness, not of incompleteness. An agent with complete preferences satisfying A+≻A∼B will also choose arbitrarily initially and regret their decision if they went ‘up’.
Example 5 is a violation of opportunism under awareness growth. This is because the agent fails to arrive at a maximal node even though the growth of the tree did not bring about any prospects that are strictly preferred to the previously present ones.
This requirement is not in general equivalent to the transitivity of weak preference.