This is a linkpost for https://arxiv.org/abs/2210.10760
Scaling Laws for Reward Model Overoptimization
15Sam Marks
2leogao
7jacob_cannell
2leogao
3Adam Jermyn
2Jacob_Hilton
1Adam Jermyn
3Charlie Steiner
2leogao
2Thomas Kwa
2leogao
2Algon
2leogao
New Comment
Excellent work!
I had previously expected that training with KL-regularization would not be equivalent to early stopping in terms of its effects on RM overfitting, so I'm quite interested to see evidence otherwise. Two questions related to this:
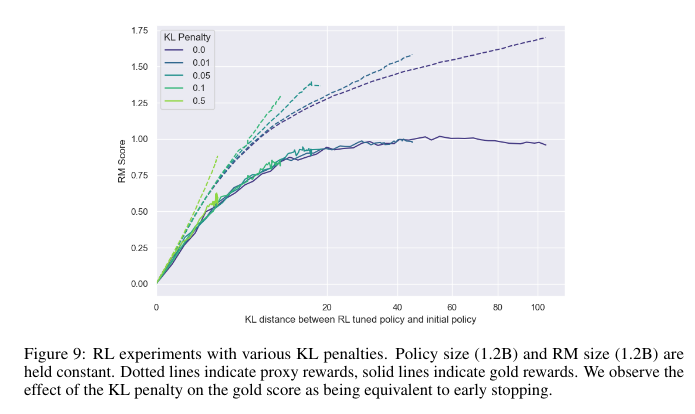
- In figure 9 of the paper (copied below), it looks like, from the perspective of the proxy RM, training with KL-regularization does not have the same effect as early stopping. This is pretty shocking to me: looking at only the gold RM lines of figure 9, you'd be tempted to guess that RL with KL penalty learns approximately the same policies as RL with early stopping; but in fact, these different training processes result in learning different policies which the gold RM happens to be indifferent between! Do you have any thoughts about what's going on here? (I'll note this seems to suggest that the RL with KL penalty <=> early stopping comparison should break down in the limit of proxy RM size and data, since if the proxy RM is very large and trained on a lot of data, then it should be a close approximation to the gold RM, in which case better KL-efficiency for the proxy RM should imply the same for the gold RM. But of course assuming that the proxy RM is much smaller than the gold RM is a more appropriate assumption in practice.)
- You mention some evidence that your results on the effects of KL penalties are especially sensitive to hyperparameters -- would you be willing to go into more detail?
Thanks!
- I don't really have a great answer to this. My guess is that it's related to the fact that the higher penalty runs do a bunch more steps to get to the same KL, and those extra steps do something weird. Also, it's possible that rather than the gold RM scores becoming more like the proxy RMs with more params/data; perhaps the changed frontier is solely due to some kind of additional exploitation in those extra steps, and evaporates when the RMs become sufficiently good.
- Mostly some evidence of other hyperparameters not leading to this behaviour, but also observing this behaviour replicated in other environments.
I found this in particular very interesting:
One can think of overfitting as a special case of Goodhart’s law where the proxy is the score on some finite set of samples, whereas our actual objective includes its generalization properties as well.
When we train on dataset X and deploy on actual data Y, that is just one level of proxy. But if you train a proxy utility function on some dataset X and then use that to train a model on dataset Y and finally deploy on actual data Z, we now have a two levels of proxy: mismatch between the proxy and the real utility function, and the standard train-test mismatch between Y and Z.
Still this analogy suggests that regularization is also the general solution to Goodharting? There is a tradeoff of course, but as you simplify the proxy utility function you can reduce overfitting and increase robustness. This also suggests that perhaps the proxy utility function should be regularized/simplified beyond that which just maximizes fit to the proxy training.
That sounds accurate. In the particular setting of RLHF (that this paper attempts to simulate), I think there are actually three levels of proxy:
- The train-test gap (our RM (and resulting policies) are less valid out of distribution)
- The data-RM gap (our RM doesn't capture the data perfectly
- The intent-data gap (the fact that the data doesn't necessarily accurately reflect the human intent (i.e things that just look good to the human given the sensors they have, as opposed to what they actually want).
Regularization likely helps a lot but I think the main reason why regularization is insufficient as a full solution to Goodhart is that it breaks if the simplest generalization of the training set is bad (or if the data is broken in some way). In particular, there are specific kinds of bad generalizations that are consistently bad and potentially simple. For instance I would think of things like ELK human simulators and deceptive alignment as all fitting into this framework.
(I also want to flag that I think in particular we have a very different ontology from each other, so I expect you will probably disagree with/find the previous claim strange, but I think the crux actually lies somewhere else)
This is really interesting, and answered a number of questions I had about fine-tuning/RLHF. I have a few more questions though (please feel free to ignore ones that are a ton of work/not worth answering in your view):
- In the caption to Figure 9 you say "We observe the effect of the KL penalty on the gold score as being equivalent to early stopping." Is this something you quantified? It's a little hard to visually make the comparison between e.g. Figure 9 and Figure 1b. Basically what I'm wondering is: Is a non-penalized model stopped at KL distance d equivalent (on the Gold RM) to a penalized model that converged to the same distance?
- Similar to (1), I'd be really interested in seeing the KL distance between an early-stopped model and a KL-penalized model (putting the early stopping threshold at the distance that the penalized model converges to). Are they close to each other (suggesting they've learned something similar, and are different from the pretrained model in the same way)?
- How much does RL reduce the entropy of the output? If you made Figure 1 with "output entropy" on the horizontal rather than KL distance would you see something similar?
Anyway, this is super cool stuff and I'm really glad to see this because I feel uneasy at how little we understand what RL/fine-tuning is doing to models relative to how much it seems to matter for performance...
- We are just observing that the gold RM score curves in Figure 9 overlap. In other words, the KL penalty did not affect the relationship between KL and gold RM score in this experiment, meaning that any point on the Pareto frontier could be reached using only early stopping, without the KL penalty. As mentioned though, we've observed this result to be sensitive to hyperparameters, and so we are less confident in it than other results in the paper.
- I don't have this data to hand unfortunately.
- I don't have this data to hand, but entropy typically falls roughly linearly over the course of training, sometimes slightly faster towards the start, and typically moving around more than KL. So I'd expect the graph to look somewhat similar, but for it to be noisier and for the functional form to not fit as well.
I haven't run many ensembling experiments so I don't have a very confident prediction. However, my guess is that it will do a lot worse if done the naive way (training each RM on a different split/shuffling of data, with max likelihood), simply because ensembling doesn't seem to work very well. I suspect it may be possible to do something fancy but I haven't looked too deeply into it.
1I thought the KL divergence is only locally a distance. You need to modify it to the JS divergence to get a distance function. Why did you choose this as a measure vs. model size and episode count? Intuitively, it isn't a crazy idea, but I'm wondering if there was something idea that made is preferable to other measures.
Unrelatedly, I don't think your interpretation of various terms in your scaling laws as a measure of goodharting makes sense. It's like, I don't see why goodharting effects should be so neatly seperable. I'll have to think up an example to see if I can explain myself properly.
Either way, this is cool work.
We mostly used KL divergence just because this is what prior works use to measure the amount of optimization done with RL. KL also has the property that it puts a hard constraint on how much the logits can change. There also isn't any particular need for it to be a distance function.
I think there is at least some subset of Regressional Goodhart (where the proxy is the gold + some noise distribution satisfying the assumptions of appendix A) that can be cleanly separated out, but I agree that the rest is a bit blurry.
TL;DR: Reward model (RM) overoptimization in a synthetic-reward setting can be modelled surprisingly well by simple functional forms. The coefficients also scale smoothly with scale. We draw some initial correspondences between the terms of the functional forms and the Goodhart Taxonomy. We suspect there may be deeper theoretical reasons behind these functional forms, and hope that our work leads to a better understanding of overoptimization.
Some other results:
If you're interested in the intersection of alignment theory and empirical research, we're hiring! We want to gain insight on things like Goodhart's Law, ELK, and inner alignment via experiments on large language models. Shoot me (leogao) a DM if you're interested.
Select figures from the paper