It is widely understood that statistical correlation between two variables ≠ causation. But despite this admonition, people are routinely overconfident in claiming correlations to support particular causal interpretations and are surprised by the results of randomized experiments, suggesting that they are biased & systematically underestimating the prevalence of confounds/common-causation. I speculate that in realistic causal networks or DAGs, the number of possible correlations grows faster than the number of possible causal relationships. So confounds really are that common, and since people do not think in DAGs, the imbalance also explains overconfidence.
Full article: http://www.gwern.net/Causality
If we allow cycles, then there are three possibilities for an edge between a pair of vertices in a directed graph: no edge, or an arrow in either direction. Since a graph of n vertices has n choose 2 pairs, the total number of DAGs of n vertices has an upper bound of 3^(n choose 2). This is much smaller than n^n.
edit: the last sentence is wrong.
Gwern, thanks for writing more, I will have more to say later.
It is much larger.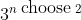 =
= 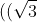 ^{n-1})^n), and
^{n-1})^n), and
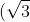 ^{n-1}) is much larger than n.
^{n-1}) is much larger than n.
3^(10 choose 2) is about 10^21.
Since the nodes of these graphs are all distinguishable, there is no need to factor out by graph isomorphism, so 3^(n choose 2) is the exact number.