Thanks for writing such a thorough article! I’d be interested in seeing how LVPMs work in practice, but I must admit I’m coming from a position of extreme skepticism: Given how complicated real-world situations like the Russia/Ukraine war are, I’m skeptical a latent variable model can provide any marginal price efficiency over a simple set of conditional and unconditional markets.
My suspicion is that if a LVPM were created for a question like “Will China invade Taiwan by 2030?” that most of the predictive power would come from people betting directly on the latent variable rather than from any model-provided updates as a result of people betting on indicator variables. The number, type, and conditional dependency graph of indicator variables is too complicated to capture in a simple model and would function worse than human intuition, imho.
Other thoughts:
- For LVPM to be useful, you’d probably want to add/remove indicator variables in real-time. What would be the process for doing this be? What is the payout of someone who bet before certain indicator variables were added? (This is sort of similar to the problems Manifold has faced in determining payouts for free-response markets.)
- Price efficiency will suffer if you can’t sell your position before resolution or can’t provide liquidity in the form of a limit order or AMM liquidity provision. I think all of these problems are solvable in theory, but may require a good deal more mathematical cleverness.
- Making a compelling UI for a LVPM is a hard problem.
- I can't make any guarantees, but the first step to getting a prototype of this up and running on Manifold (or elsewhere) would be creating a typescript npm package with the market logic. You might be able to convince me to work on this at our next hackathon...
Thanks for the reply!
Given how complicated real-world situations like the Russia/Ukraine war are, I’m skeptical a latent variable model can provide any marginal price efficiency over a simple set of conditional and unconditional markets.
When you say "a simple set of conditional and unconditional markets", what do you have in mind?
Edit: I mean for a specific case such as the Russia/Ukraine war, what would be some conditional and unconditional markets that could be informative? (I understand how conditional and unconditional markets work in principle, I'm more interested in how it would practically compete with LVPMs.)
My suspicion is that if a LVPM were created for a question like “Will China invade Taiwan by 2030?” that most of the predictive power would come from people betting directly on the latent variable rather than from any model-provided updates as a result of people betting on indicator variables. The number, type, and conditional dependency graph of indicator variables is too complicated to capture in a simple model and would function worse than human intuition, imho.
So I am not 100% sure what you are referring to here. When you are talking about "model-provided updates as a result of people betting on indicator variables", I can think of two things you might be referring to:
- If someone bets directly on a market , i.e. changing to a new value, then (using some math) we can treat this as evidence to update , using the fact that we know .
- If someone bets on a conditional market , then the parameters of this conditional market may change, which in a sense constitutes an update as a result of people betting on indicator variables.
- (Possibly something else?)
Your language makes me think you are referring to 1, and I agree that this will plausibly be of limited value. I'm most excited about 2 because it allows people to better aggregate information about the plausible outcomes, while taking correlations into account.
- For LVPM to be useful, you’d probably want to add/remove indicator variables in real-time. What would be the process for doing this be? What is the payout of someone who bet before certain indicator variables were added? (This is sort of similar to the problems Manifold has faced in determining payouts for free-response markets.)
You can treat the addition or removal of an indicator as a trade performed by the market owner. The payout for a person for a trade does not depend on any trades that happen after the person's . (This follows from the fact that we describe the payoffs as a function of the probabilities just before and just after .) So the owner of the market can add and remove however many indicator variables they want without any trouble.
- Price efficiency will suffer if you can’t sell your position before resolution or can’t provide liquidity in the form of a limit order or AMM liquidity provision. I think all of these problems are solvable in theory, but may require a good deal more mathematical cleverness.
I think the part of my scoring counts as an AMM liquidity provision? I might be misunderstanding what AMM liquidity provision means.
To scale up the liquidity, one can multiply this expression by the expression by some constant so there is a deeper pool of liquidity.
Of course, a consequence of this is that the person creating the latent variable market has to provide enough liquidity to cover this, i.e. to create a market with a starting state , they would have to pay . In practice I would assume is like 1, so it reduces to , which for e.g. a predicting uniform distribution over would be where is the number of indicators.
- Making a compelling UI for a LVPM is a hard problem.
At first glance this seems true; my UI seems to have confused people. However, I am not a designer.
I should probably repeat my request for a designer to work with.
- I can't make any guarantees, but the first step to getting a prototype of this up and running on Manifold (or elsewhere) would be creating a typescript npm package with the market logic. You might be able to convince me to work on this at our next hackathon...
Hm, this sounds like a task that would be relatively isolated from the rest of your codebase, and therefore something I could do independently without learning much of Manifold Market's code? I would be up for programming this. Do you have any examples of similar modules in your codebase right now that I can look at, to see what interface it should provide?
When you say "a simple set of conditional and unconditional markets", what do you have in mind?
Unconditional: "Will China invade Taiwan by 2030?"; Conditional: "If China experiences a recession any time before 2030, will China invade Taiwan by 2030?"
Your language makes me think you are referring to 1, and I agree that this will plausibly be of limited value.
Isn't estimating from most of the value of LVPMs?!
I think the part of my scoring counts as an AMM liquidity provision?
Yes, that's correct; if the market creator is willing to issue these payouts, then they are playing the role of AMM.
The question is how to add third-party liquidity provision to this system, i.e. where users can inject and remove liquidity from the market to increase payouts for traders (ideally while being compensated for their efforts).
Hm, this sounds like a task that would be relatively isolated from the rest of your codebase, and therefore something I could do independently without learning much of Manifold Market's code?
That's the idea. You can see some example code for our Uniswap-style AMM here, but honestly, any well-designed api would be fine. What I'd like is: 1. A typescript interface that defines the current state of a LVPM at any given point, 2. Betting function: Given a bet on some variable and the current market state, return the new market state and user position, 3. Resolution function: given the current market state, the final outcome of the market, and a list of user positions, return a list of all the user payouts.
Unconditional: "Will China invade Taiwan by 2030?"; Conditional: "If China experiences a recession any time before 2030, will China invade Taiwan by 2030?"
...
Isn't estimating from most of the value of LVPMs?!
Kind of. The point is to estimate . However, the value is not supposed to come from automatically estimating , but rather from providing an objective way of scoring manual predictions about P(Y) when we don't have an objective definition of .
I agree that if the goal was to automatically predict from , structures of conditional prediction markets seems better. See also the "Latent variable markets vs combinatorial markets" section of my post; there are some cases where e.g. is more interesting.
So basically, yes, the value of LVPMs comes from estimating , but the way we estimate is by having people make predictions on . All the elaborate has the primary purpose of providing a way to objectively score predictions on , and a secondary purpose of providing information/common knowledge about the domain of applicability of the concept.
Yes, that's correct; if the market creator is willing to issue these payouts, then they are playing the role of AMM.
One thing I guess I should note is that the market maker only has to pay the first person. To clarify how this works, suppose the market maker creates a market with initial state , and a first trader then updates this state to , and a second trader then updates the state to . Assuming for simplicity that the initial distribution is uniform over , when the market resolves to a specific , we can then read the payoffs here:
- The second trader gets a payout of .
- The first traders gets a payout of .
- The market maker paid for making the market, which we can think of them as getting a payout of to make the signs of the expressions all aligned.
If we add all of these payouts up, we get , which in general is a nonpositive number[1], and so the market will never give a greater payout than what is put in. Essentially what happens is that each trader pays off the next trader, guaranteeing that it all adds up. (This won't require the individual traders to pay any huge amount of money, because they are always paying relative to , which accounts for most of the pool.)
The question is how to add third-party liquidity provision to this system, i.e. where users can inject and remove liquidity from the market to increase payouts for traders (ideally while being compensated for their efforts).
I think if people add some additional liquidity, one can just find a new scale factor on the payoffs that continues to make everything add up?
That's the idea. You can see some example code for our Uniswap-style AMM here, but honestly, any well-designed api would be fine. What I'd like is: 1. A typescript interface that defines the current state of a LVPM at any given point, 2. Betting function: Given a bet on some variable and the current market state, return the new market state and user position, 3. Resolution function: given the current market state, the final outcome of the market, and a list of user positions, return a list of all the user payouts.
Thanks! I'll take a look.
I'm thinking I should maybe implement LVPMs based on latent class analysis rather than item response theory because it is easier to design an interface for and get an intuition for (since LCA literally just enumerates the set of possible outcomes).
- ^
though presumably often rather than just , because as the close date nears, \vec x is going to be better and better known, and so the probaility is going to move towards 1
I can't see anything that pins down the latent variable other than Schelling point inertia. Or do interpretations that support correlation intrinsically get favored?
If I understand your question correctly, then yes, interpretations that support correlation intrinsically get favored.
Strictly speaking, there is a sense in which we can entirely ignore when understanding what the latent variable markets are doing. A latent variable market over a set of variables is really trying to predict their join distribution . If these variables are all "getting at the same thing" from different angles, then they will likely "fall within a subspace", and it is this subspace that the LVPMs are characterizing.
For instance consider the following plot of a probability distribution:
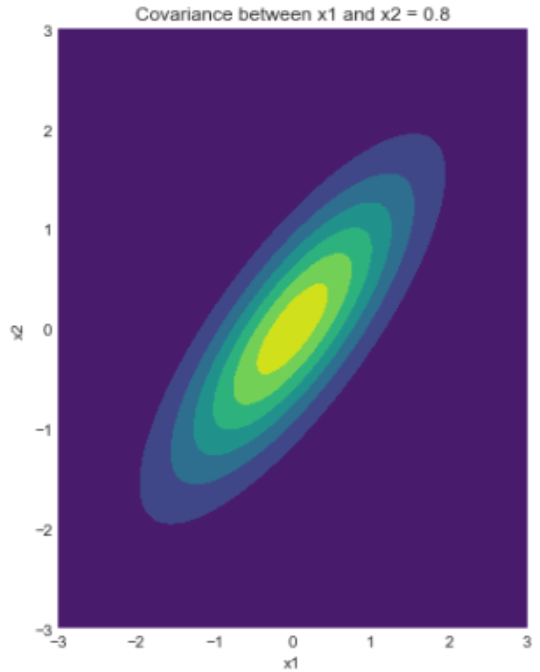
There is a ridge where x1 and x2 are similar in magnitude, and most of the probability mass is distributed along that ridge. It is unlikely for x1 to be 1 while x2 is -1, or vice versa.
The LVPMs characterize this ridge of high probability, so an LVPM on a probability distribution like the above would likely range from "x1 and x2 are both low" to "x1 and x2 are both high".
If you are familiar with principal component analysis, it may be helpful to think of LVPMs as doing a similar thing.
So if I'm understanding correctly, you're saying a LVPM market Y could be displayed without a title, and traders would still converge toward finding the joint probability distribution function? So instead of making a LVPM titled "Will Ukraine do well in defense against Russia?", I could make a LVPM that says "Hey, here are a bunch of existing objective questions that may or may not be correlated, have at it", and it would be just as functional?
If so that's pretty neat. But what stops Trader1 from interpreting Y as "Will Ukraine do well in defense against Russia?" while Trader2 treats it as "Will Russia do well in the invasion of Ukraine?" IIUC, these two traders would make nearly opposite trades on the conditional probabilities between each X and Y.
So if I'm understanding correctly, you're saying a LVPM market Y could be displayed without a title, and traders would still converge toward finding the joint probability distribution function? So instead of making a LVPM titled "Will Ukraine do well in defense against Russia?", I could make a LVPM that says "Hey, here are a bunch of existing objective questions that may or may not be correlated, have at it", and it would be just as functional?
Yep.
If so that's pretty neat. But what stops Trader1 from interpreting Y as "Will Ukraine do well in defense against Russia?" while Trader2 treats it as "Will Russia do well in the invasion of Ukraine?" IIUC, these two traders would make nearly opposite trades on the conditional probabilities between each Xi and Y.
So this is in fact true: LVPMs will not be totally unique, but instead have symmetries where some options do equally well. The exact type of symmetry depends on the kind of market, but they mainly look like what you describe here: swapping around the results such that yes becomes no and no becomes yes.
The way I usually handle that problem is by picking one of the indicators as a "reference indicator" and fixing it to have a specific direction of relationship with the outcome. If the reference indicator cannot be flipped, then all the other indicators have to have a fixed direction too. (One could also do something more nuanced, e.g. pick many reference indicators.)
I don't know whether this is necessary for humans. I mainly do this with computers because computers have no inherent idea which direction of the LV is most natural for humans.
I don't know if it would be a problem for people. It's not something that happens iteratively; while you can flip all the parameters at once and still get a good score, you cannot continuously change from one optimum to an opposite optimum without having a worse score in the middle. So if it is an issue, it will probably mainly be an issue with trolls.
So this is in fact true: LVPMs will not be totally unique, but instead have symmetries where some options do equally well. The exact type of symmetry depends on the kind of market, but they mainly look like what you describe here: swapping around the results such that yes becomes no and no becomes yes.
I'm not a savvy trader by any means, but this sets off warning bells for me that more savvy traders will find clever exploits in LVPMs. You can't force anyone to abide by the spirit of the market's question, they will seek the profit incentive wherever it lies.
(I feel somewhat satisfied that the "question reversal" symmetry is ruled out by the market maker restricting the possible PDF space (in half along one specified dimension, IIUC). I'm curious how that would be practically implemented in payouts.)
I worry about these other possible symmetries or rotations, which I can't yet wrap my head around. I would love an illustrating example showing how they work and why we should or shouldn't worry about them.
I'm not a savvy trader by any means, but this sets off warning bells for me that more savvy traders will find clever exploits in LVPMs. You can't force anyone to abide by the spirit of the market's question, they will seek the profit incentive wherever it lies.
Hmm I'm not sure what exploits you have in mind. Do you mean something like, they flip the meaning of the market around, and then people who later look at the market get confused and bet in the opposite direction of what they intended? And then the flipper can make money by undoing their bets?
Or do you mean something else?
I feel somewhat satisfied that the "question reversal" symmetry is ruled out by the market maker restricting the possible PDF space (in half along one specified dimension, IIUC).
Yep, in half along one specified dimension.
I'm curious how that would be practically implemented in payouts.
There's a few different ways.
If someone bets to set the market state to a that flips the fixed dimension, the market implementation could just automatically replace their bet with so it doesn't flip the dimension. The payouts are symmetric under flips, so they will get paid the same regardless of whether they bet or .
Alternatively you could just forbid predictions in the UI that flip the fixed dimension.
I worry about these other possible symmetries or rotations, which I can't yet wrap my head around. I would love an illustrating example showing how they work and why we should or shouldn't worry about them.
Flipping is the only symmetry that exists for unidimensional cases.
If you have multiple dimensions, you have a whole continuum of symmetries, because you can continuously rotate the dimensions into each other.
Thanks for being patient with my questions. I'm definitely not solid enough on these concepts yet to point out an exploit or misalignment. It would be super helpful if you fill out your LVPM playground page in the near future with a functional AMM to let people probe at the system.
Flipping is the only symmetry that exists for unidimensional cases.
If you have multiple dimensions, you have a whole continuum of symmetries, because you can continuously rotate the dimensions into each other.
What do you mean by unidimensional cases? So like if the binary LVPM is made up of binary markets to , I would have called that an N-dimensional case, since the PDF is N-dimensional. How many symmetries and "possible convergences" does this have?
Thanks for being patient with my questions.
No problem, answering questions is the point of this post. 😅
It would be super helpful if you fill out your LVPM playground page in the near future with a functional AMM to let people probe at the system.
The playground page already has this. If you scroll down to the bottom of the page, you will see this info:
To play with the payout and get an intuition for it, you can use the checkboxes below. Your bets have currently cost proportional to 0 Mana, and if the outcome below happens, you get a payout proportional to 0 Mana, for a total profit proportional to 0 Mana.
- Japan hyperinflation by 2030?
- US hyperinflation by 2030?
- Ukraine hyperinflation by 2030?
If you make bets, then the numbers in this section get updated with the costs and the payouts.
But I guess my interface probably isn't very friendly overall, even if it is there. 😅
What do you mean by unidimensional cases? So like if the binary LVPM is made up of binary markets to , I would have called that an N-dimensional case, since the PDF is N-dimensional. How many symmetries and "possible convergences" does this have?
I am talking about the dimensionality of , not the dimensionality of .
In the markets I described in the post and implemented for my demo, is always one-dimensional. However, it is possible to make more advance implementations where can be multidimensional. For instance in the uncertainty about the outcome of the Ukraine war, there is probably not just a Ukraine wins <-> Russia wins axis, but also a war ends <-> war continues axis.
I really liked this post when I read it, even though I didn't quite understand it to my satisfaction (and still don't).
As far as I understand the post, it proposes a concrete & sometimes fleshed-out solution for the perennial problem of asking forecasting questions: How do I ask a forecasting question that actually resolves the way I want it to, in retrospective, and doesn't just fall on technicalities?
The proposed solution is latent variables and creating prediction markets on them: The change in the world (e.g. AI learning to code) is going to affect a bunch of different variables, so we set up a prediction market for each of those, and then (through some mildly complicated math) back out the actual change in the latent variable, not just the technicalities on each of the markets.
This is pretty damn great: It'd allow us to more quickly communicate changes in predictions about the world to people and read prediction market changes more easily. The downside is that betting on such markets would be more complicated and effortful, and especially for non-subsidized markets that is often a breaking point. (Many "boring" Metaculus questions receive <a few dozen predictions.)
I'm pretty impressed by this work, and wish there was some efforts at integration into existing platforms. Props to tailcalled for writing code and an explanation for this post. I'll give it +4, maybe even +9, because it represents genuine progress on a tricky intellectual question.
Prediction markets are good at eliciting information that correlates with what will be revealed in the future, but they treat each piece of information independently. Latent variables are a well-established method of handling low-rank connections between information, and I think this post does a good job of explaining why we might want to use that, as well as how we might want to implement them in prediction markets.
Of course the post is probably not entirely perfect. Already shortly after I wrote it, I switched from leaning towards IRT to leaning towards LCA, as you can see in the comments. I think it's best to think of the post as staking out a general shape for the idea, and then as one goes to implementing it, one can adjust the details based on what seems to work the best.
Overall though, I'm now somewhat less excited about LVPMs than I was at the time of writing it, but this is mainly because I now disagree with Bayesianism and doubt the value of eliciting information per se. I suspect that the discourse mechanism we need is not something for predicting the future, but rather for attributing outcomes to root causes. See Linear Diffusion of Sparse Lognormals for a partial attempt at explaining this.
Insofar as rationalists are going to keep going with the Bayesian spiral, I think LVPMs are the major next step. Even if it's not going to be the revolutionary method I assumed it would be, I would still be quite interested to see what happens if this ever gets implemented.
I don't know of a neat way to achieve this with latent variable markets. So I guess it won't be supported?
Actually, I suppose one could use gradient descent to figure out a trade that gives the largest guaranteed profit, and then implement that trade? That would be sort of like selling one's shares. I don't know how well that would work in practice though. I suspect it would work OK?
Bayesian networks support latent variables, and so allowing general Bayesian networks can be considered a strict generalization of allowing latent variables, as long as one remembers to support latent variable in the Bayesian network implementation.
Correct me if I'm wrong, but I believe this isn't necessarily true.
The most general Bayesian network prediction market implementation I'm aware of is the SciCast team's graphical model market-maker. Say a trader bets up a latent variable -- and this correctly increases the probability of its child variables (which all resolve True).
Under your model you would (correctly, IMO) reward the trader for this, because you are scoring it for the impact it has on the resolved variables. But under their model, another trader can come and completely flip , while also adjusting each conditional probability -- without affecting the overall score of the model, but screwing over the first trader completely because the first trader just owns some stocks which are now worth much less.
Your linked paper is kind of long - is there a single part of it that summarizes the scoring so I don't have to read all of it?
Either way, yes, it does seem plausible that one could create a market structure that supports latent variables without rewarding people in the way I described it.
Epistemic status: I am probably misunderstanding some critical parts of the theory, and I am quite ignorant on technical implementation of prediction markets. But posting this could be useful for my and others' learning.
First question. Am I understanding correctly how the market would function. Taking your IRT probit market example, here is what I gather:
(1) I want to make a bet on the conditional market P(X_i | Y). I have a visual UI where I slide bars to make a bet on parameters a and b; (dropping subscript i) however, internally this is represented by a bet on a' = a sigma_y and P(X) = Phi(b'/sqrt(a'+1)), b' = b + a mu_y. So far, so clear.
(2) I want to bet on the latent market P(Y). I make bet on mu_Y and sigma_y, which is internally represented by a bet on a' and P(X). In your demo, this is explicit: P(Y) actually remains a standard normal distribution, it is the conditional distributions that shift.
(3) I want to bet on the unconditional market P(X_i), which happens to be an indicator variable for some latent variable market I don't really care about. I want to make a bet on P(X_i) only. What does exactly happen? If the internal technical representation is a database row [p_i, a'] changing to [p_new, a'], then I must be implicitly making a bet on a' and b' too, as b' derived from a and P(X) and P(X) changed. In other words, it appears I am also making a bet on the conditional market?
Maybe this is OK if I simply ignore the latent variable market, but I could also disagree with it: I think P(X) is not correlated with the other indicators, or the correlation structure implied by linear probit IRT model is inadequate. Can I make a bet of form [p_i, NA] and have it not to participate in the latent variable market structure? (Ie when the indicator market resolves, p_i is taken into account for scoring, NA is ignored while scoring Y).
Thus, I can launch a competing latent variable market for the same indicators? How can I make a bet against a particular latent structure in favor of another structure? A model selection bet, if you will.
Context for the question: In my limited experience of latent variable models for statistical inference tasks, the most difficult and often contested question is whether the latent structure you specified is good one. The choice of model and interpretations of it are very likely to get criticized and debated in published work.
Another question for discussion.
It seems theoretically possible to obtain individual predictors' bets / predictions on X_1 ... X_k, without presence of any latent variable market, impute for the missing values if some predictors have not predicted on all k indicators, and then estimate a latent variable model on this data. What is the exact benefit of having the latent model available for betting? If fit a Bayesian model (non-market LVM with indicator datapoints) and it converges, from this non-market model, I would obtain posterior distribution for parameters and compute many of the statistics of interest.
Presumably, if there is a latent "ground truth" relationship between all indicator questions and the market participants are considering them, the relationship would be recovered by such analysis. If the model is non-identifiable or misspecified (= such ground truth does not exist / is not recoverable), I will have problems fitting it and with the interpretation of fit. (And if I were to run a prediction market for a badly specified LVM, the market would exhibit problematic behavior.)
By not making a prediction market for the latent model available, I won't have predictions on the latent distribution directly, but on the other hand, I could try to estimate several different without imposing any of their assumptions about presumed joint structure on the market. I could see this beneficial, depending on how the predictions on Y "propagate" to indicator markets or the other way around (case (3) above).
Final question for discussion: Suppose I run a prediction market using the current market implementations (Metaculus or Manifold or something else, without any LVM support), where I promise to fit a particular IRT probit model at time point t in future and ask for predictions on the distribution of posterior model parameters estimates when I fit the model. Wouldn't I obtain most of the benefits of "native technical implementation" of a LVM market ... except that updating away any inconsistencies between the LVM prediction market estimate and individual indicator market will be up to to individual market participants? The bets on this estimated LVM market at least should behave as any other bets, right? (Related: which should be the time point t when I promise to fit the model and resolve the market? t = when the first indicator market resolves? when the last indicator market resolves? arbitrary fixed time point T?)
(1) I want to make a bet on the conditional market P(X_i | Y). I have a visual UI where I slide bars to make a bet on parameters a and b; (dropping subscript i) however, internally this is represented by a bet on a' = a sigma_y and P(X) = Phi(b'/sqrt(a'+1)), b' = b + a mu_y. So far, so clear.
Yep.
(Or maybe not a and b, but some other parameterization; I would guess the most intuitive UI is still an open question.)
(2) I want to bet on the latent market P(Y). I make bet on mu_Y and sigma_y, which is internally represented by a bet on a' and P(X). In your demo, this is explicit: P(Y) actually remains a standard normal distribution, it is the conditional distributions that shift.
Yep.
(3) I want to bet on the unconditional market P(X_i), which happens to be an indicator variable for some latent variable market I don't really care about. I want to make a bet on P(X_i) only. What does exactly happen? If the internal technical representation is a database row [p_i, a'] changing to [p_new, a'], then I must be implicitly making a bet on a' and b' too, as b' derived from a and P(X) and P(X) changed. In other words, it appears I am also making a bet on the conditional market?
Maybe this is OK if I simply ignore the latent variable market, but I could also disagree with it: I think P(X) is not correlated with the other indicators, or the correlation structure implied by linear probit IRT model is inadequate. Can I make a bet of form [p_i, NA] and have it not to participate in the latent variable market structure? (Ie when the indicator market resolves, p_i is taken into account for scoring, NA is ignored while scoring Y).
Thus, I can launch a competing latent variable market for the same indicators? How can I make a bet against a particular latent structure in favor of another structure? A model selection bet, if you will.
Context for the question: In my limited experience of latent variable models for statistical inference tasks, the most difficult and often contested question is whether the latent structure you specified is good one. The choice of model and interpretations of it are very likely to get criticized and debated in published work.
Good question! This is actually a problem that I didn't realize at the time I started promoting LVPMs, though I did realize it somewhere along the way, albeit underestimating it and expecting it to solve itself, though somewhere along the way I realized that I had underestimated it. I still think it is only a very minor problem, but lemme give my analysis:
There are multiple ways to implement this type of bet, and your approach of changing [p_old, a'] to [p_new, a'] is only one of them; it was the one I favored earlier on, but there's an alternate approach that others have favored, and in fact there's a first approach that I've now come to favor. Let's take all of them.
The approach described by my post/by you: Assuming that we change the internal representation in the database from [p_old, a'] to [p_new, a'], this is equivalent to making a bet on the latent variable market that only affects b. So essentially you would be making a bet that b has higher probability across the entire latent variable.
As part of my initial push, I made the mistake of assuming that this was equivalent to just making a bet on X without the latent variable market, but then later I realized I was mixing up negative log probs and logits (you are making a bet that b has higher logit across the latent variable, but a prediction market without latent variables would be making a bet that b has higher negative log probabilities, not higher logits).
Conventional approach: I think the approach advocated by e.g. Robin Hanson is to have one grand Bayes net structure for all of the markets that anyone can make predictions on, and then when people make a prediction on only a subset of the structure, such as an indicator variable, then that bet is treated as virtual evidence which is used to update the entire Bayesian network.
This is basically similar in consequences to what you describe: if people make a bet on some indicator variable, they make implied bets on lots of other things too. However the implied bets are more complicated and less risky to the better than the version described in my post. (When I had written the post, I hadn't realized those complexities.)
In order to make a model selection bet, you would bet directly on the Bayes net structure that hangs around all of the markets, rather than betting on X directly.
I think the conventional approach has traditionally mainly struggled because it's had to deal with making Bayesian updates on a huge Bayes net. I would prefer something more atomic/discrete, and I would not be surprised if Manifold Markets would prefer something more atomic/discrete too. Treating it as Bayesian updates is also a bit of a problem for certain latent variable models, since e.g. if you fix the distribution of your latent variable to be Gaussian, then there are certain Bayesian updates that you cannot exactly do.
My new preferred approach: Rather than thinking of the LVPM as sharing parameters with the indicator markets (i.e. the model), I'd probably be inclined to give it separate parameters (i.e. a model). Of course then the trouble is that we could enter into an inconsistent state where the probabilities implied by the LVPM do not equal the probabilities from the indicator markets.
Ideally to minimize confusion and maximize information flow, we would like to go from an inconsistent state to a consistent state as quickly as possible. I think this could be done with an arbitrage bot (it seems like most of the time this would probably be +EV, so the bots should remain solvent), though perhaps the market should offer users to automatically make the arbitrage bets themselves so they can benefit from the presence of the latent variables.
I expect to give an update on this later with more formal derivations, likely together with my implementation of latent class markets for Manifold.
It seems theoretically possible to obtain individual predictors' bets / predictions on X_1 ... X_k, without presence of any latent variable market, impute for the missing values if some predictors have not predicted on all k indicators, and then estimate a latent variable model on this data. What is the exact benefit of having the latent model available for betting? If fit a Bayesian model (non-market LVM with indicator datapoints) and it converges, from this non-market model, I would obtain posterior distribution for parameters and compute many of the statistics of interest.
Presumably, if there is a latent "ground truth" relationship between all indicator questions and the market participants are considering them, the relationship would be recovered by such analysis. If the model is non-identifiable or misspecified (= such ground truth does not exist / is not recoverable), I will have problems fitting it and with the interpretation of fit. (And if I were to run a prediction market for a badly specified LVM, the market would exhibit problematic behavior.)
By not making a prediction market for the latent model available, I won't have predictions on the latent distribution directly, but on the other hand, I could try to estimate several different without imposing any of their assumptions about presumed joint structure on the market. I could see this beneficial, depending on how the predictions on Y "propagate" to indicator markets or the other way around (case (3) above).
Strictly speaking, it's an empirical question how well this would work.
I could certainly imagine programmatically fitting a latent variable model to prediction market data, assuming that there is a fixed set of outcomes and the users mainly disagree about the latent variable values. However, it seems to me that this would run into massive problems due to e.g. Kelly betting where people don't update the probabilities all the way to match their beliefs. You could probably attempt to model the participant's risk aversion etc., but I have a hard time believing that it would work.
Final question for discussion: Suppose I run a prediction market using the current market implementations (Metaculus or Manifold or something else, without any LVM support), where I promise to fit a particular IRT probit model at time point t in future and ask for predictions on the distribution of posterior model parameters estimates when I fit the model. Wouldn't I obtain most of the benefits of "native technical implementation" of a LVM market ... except that updating away any inconsistencies between the LVM prediction market estimate and individual indicator market will be up to to individual market participants? The bets on this estimated LVM market at least should behave as any other bets, right?
Asking for predictions about the parameters of the model would make it more like a method of moments estimator than a maximum likelihood estimator, right? Or maybe not, it seems kind of hard to predict how exactly it would go.
Regardless, I don't think this is an unreasonable idea to experiment with, but I think there are two challenges:
- As mentioned, I'm pretty skeptical of the notion that you can fit LV models to prediction market predictions and have it work well.
- If you don't have LVPM support, the UI for making predictions would probably be even worse than the UI I made.
I think if this was somehow changed to be maximum likelihood, and if those two challenges were removed, then you would get something close to "My new preferred approach".
P(→Xi)=∑jpj∏iXiqi,j+(1−Xi)(1−qi,j)
Maybe I'm missing something, but if we are estimating the P(Xi), how can we also have Xi on RHS? and what is the adjustment +(1−Xi)(1−qi,j). why is that there?
Maybe I'm missing something, but if we are estimating the P(Xi), how can we also have Xi on RHS?
These probabilities are used for scoring predictions over the observed variables once the market resolves, so at that point we "don't need" P(Xi) because we already know what Xi is. The only reason we compute it is so we can reward people who got the prediction right long ago before Xi was known.
and what is the adjustment +(1−Xi)(1−qi,j). why is that there?
Xiqi,j+(1−Xi)(1−qi,j) is equivalent to "qi,j if Xi = 1; otherwise 1-qi,j if Xi = 0". It's basically a way to mathematize the "contigency table" aspect.
I've been pushing for latent variables to be added to prediction markets, including by making a demo for how it could work. Roughly speaking, reflective latent variables allow you to specify joint probability distributions over a bunch of observed variables. However, this is a very abstract description which people tend to find quite difficult, which probably helps explain why the proposal hasn't gotten much traction.
If you are familiar with finance, another way to think of latent variable markets is that they are sort of like an index fund for prediction markets, allowing you to make overall bets across multiple markets. (Though the way I've set them up in this post differs quite a bit from financial index funds.)
Now I've just had a meeting with some people working at Metaculus, and it helped me understand what sorts of questions people might have about latent variables for prediction markets. Therefore, I thought it would be a good idea to write this post, both so the people at Metaculus have it as a reference if they want to implement it, and so that others who might be interested can learn more.
As a further note, I have updated my demo with more descriptions. It now attempts to explain the meaning of the market (e.g. "The latent variable market works by having a continuum of possible latent outcomes, ..."), as well has how different kinds of evidence might map to different predictions (e.g. "If you think you have seen evidence that narrows down the distribution of outcomes relative to the market beliefs, ..."). Furthermore, I have updated the demo to be somewhat nicer and somewhat more realistic, though it is still somewhat crude. I would be interested in hearing more feedback in the comments.
I should note that if you are interested in implementing latent variables in practice for prediction markets, I am very interested in helping with that. I have an "Offers" section at the end of the post, where I offer advice, code and money for the project.
Use cases
There are a number of situations where I think latent variables are extremely helpful:
These are still quite abstract, so I am going to give some concrete examples of how they could apply. For this section, I will be treating latent variables "like magic"; I will describe the interface people use to interact with them, but I will be ignoring the mathematics underlying them. If you would like to learn about the math, skip to the technical guide.
Detecting and adjusting for random measurement error
Example: AI learning to code
Suppose you want to know whether AI will soon learn to code better than a human can. Maybe you can find four prediction markets on it with different criteria:
Without latent variables: These all seem like reasonable proxies for whether AI has learned to code. However, it is unclear how accurate they all are. If the prediction markets give each of them a decades-wide distribution, but with a 5 year gap between each of the means, does that mean that:
Both of these are compatible with the prediction market distributions. The first case corresponds to the assumption of a 100% correlation between the different outcomes, while the latter case corresponds to the assumption of a 0% correlation between the different outcomes.
The way we should think of the market in practice depends very much on the degree of correlation. If they are highly correlated, we can take successes in benchmarks to be a fire alarm for imminent practical changes due to AI, and we can think of AI capabilities in a straightforward unidimensional way, where AI becomes better across a wide variety of areas over time. However, if they are not very correlated, then it suggests that we have poor concepts, bad resolution criteria, or are paying attention to the wrong things.
Realistically I bet it is going to be in between those extremes. Obviously the correlation is not going to be 0%, since all the markets depend on certain shared unknowns, like how difficult programming is going to be for AI, or how much investment the area is going to receive. However, it is also not going to be 100%, because each outcome also hasunique unknowns. Bloggers regularly end up making a wrong call, benchmarks may turn out to be easier or harder than expected, and so on. Even seemingly solid measures like engineer count may fail, if the meaning of the software engineer job changes a lot. But knowing where exactly the degree of correlation falls between the extremes seems like an important question.
With latent variables: We can think of this as being a signal/noise problem. There is some signal you want to capture (AI coding capabilities). However, every proxy you can come up with for the signal has some noise.
Latent variables separate the signal and the noise. That is, you find (or create) a latent variable market that includes all of these outcomes, or more. This market contains a probability distribution for the noiseless/"true" version of the question, "When will AI code as well as humans do?". Furthermore, it also contains conditional distributions, P(When will AI beat the best humans at a specific programming benchmark?|When will AI code as well as humans do?).
How does the market know what the distributions will be? It spreads the task out to its participants:
Of course this is just a vague qualitative explanation. See the technical guide for more.
This sort of market also lets you learn something about the amount of measurement error there is. For instance, if the market says that all of your indicators are almost entirely independent, then that implies that there is too much measurement error for them to be useful. On the other hand, if the market says that they are closely correlated, then that seems to suggest that you don't have much to worry about with regards to measurement error. If you care, then you can use this information to figure out how many indicators are needed to make the resolution of the overall question quite objective (though latent variable markets work even if there is so much noise that the answer to the overall question is subjective).
Summary on measurement error
In prediction markets, you have to specify fairly objective outcomes, so that people can use those outcomes for predictions. However, these objective outcomes might be imperfect representations of what you really intended to learn about.
If you are betting on the markets, this can lead to the actual resolution of a question being the opposite of what the resolution should have been in spirit. Furthermore, since you can know ahead of time that this might happen, this incentivizes you to make less confident predictions, as you cannot rely on the resolution being correct. If someone else wishes to use these predicted probabilities in practice, they can't take the predictions at face value, but have to take distortions in the market predictions into account.
Latent variables reduce this problem by having multiple resolution criteria, and then separating the distribution of the true underlying reality from the relationship between the underlying reality and the resolution criteria.
Abstracting over conceptually related yet distinct variables, and ranking the importance of different pieces of information
Example: Ukraine defense performance
Prediction markets contain various predictions about outcomes that seem relevant for Ukraine's performance in the defense against Russia. For instance, Manifold Markets has the following questions:
Clearly these sorts of markets say something about Ukraine's performance. However, also clearly, they are too narrow to be taken as The Final Truth About The War. Instead, they are components and indicators of how well things are going, in terms of military strength/government capacity, ally support, etc..
There's in a sense an abstract aggregate of "all the things which might help or hurt Ukraine performance", and when I look up predictions about the Ukraine war, I am mainly interested in the distribution of this abstract aggregate, not so much about the specific questions, because it is the abstract aggregate that tells me what to expect with many other questions further out in the future. (Maybe if you were Ukranian, this would be somewhat different, e.g. someone who has a lot of hryvnia might care a lot about hyperinflation.)
Without latent variables: We can look up the probabilities for these questions, and they give us some idea of how well it is going for Ukraine overall. However, these probabilities don't characterize abstract things about Ukraine's performance very well. For instance, they cannot distinguish between the following two possibilities:
Again, I bet it is going to be somewhere between the extremes, but I don't know where on that continuum it will fall.
With latent variables: We can find a latent variable market that contains tons of questions about Ukraine's defense performance. This allows you to get predictions for the entire range of possible outcomes, in a sense acting as an "index fund" for how well Ukraine will do. You can get predictions for what happens if Ukraine's defense goes as well as expected, but also predictions for what happens if it goes realistically better than expected, or realistically worse than expected. You can even sample from the distribution, to get a list of scenarios with different outcomes.
The underlying principle is basically the same as for measurement error, but let's take a couple of example of how the betting works anyway.
The latent variable markets also tell you what to pay attention to. Realistically, some of the concrete variables are going to be very noisy. For instance, maybe we expect control of Crimea to flip multiple times, and that who exactly controls it depends on subtle issues of timing between strikes. In that case, maybe the market doesn't think that control of Crimea will be all that correlated with other distant outcomes, and that would probably make me not pay very much attention to news about Crimea.
Summary of abstraction
Again, in prediction markets you have to specify fairly objective outcomes. In order to define an outcome objectively, it is helpful to make it about something concrete and narrow. However, you probably usually don't care so much about concrete and narrow things - instead you care about things that have widespread, long-range implications.
This doesn't mean prediction markets are useless, because concrete and narrow things will often be correlated with factors that have long-range implications. However, those correlations are often not perfect; there may be tons of contextual factors that matter for which things exactly happen, or there may be multiple ways of achieving the same result, or similar.
This can be addressed with abstraction; we can consider the concrete variables to be instances or indicators of some underlying trend. As long as these concrete variables are sufficiently correlated, this underlying trend becomes a useful way to think about and learn about the world. Latent variables provide a way specify distributions involving this underlying trend.
Once you have this distribution, latent variables also provide a way of ranking different concrete variables by the degree to which they correlate with the latent variable. This might be useful, e.g. to figure out what things are worth paying attention to.
Better conditional markets
Example: Support of Taiwan in War
Without latent variables: There's strong tensions between China and Taiwan, to the point where China might go to war with Taiwan soon. However, it hasn't happened yet. If China goes to war with Taiwan, we might want to know what will happen - e.g. whether the US will support Taiwan in the war, or whether the war will escalate to nukes, or various other questions.
To know what will happen under some condition, one can use conditional prediction markets. These markets only resolve when the condition is met, which should make their probability estimate match the actual conditional probability given the condition. So you could for instance have a resolution criterion of "If China declares war on Taiwan, will the US provide weapons to support Taiwan?".
However, this sort of criterion could become a problem; for instance, Putin didn't declare war on Ukraine when Russia invaded Ukraine, so maybe China also wouldn't declare war on Taiwan. You could perhaps fix that by using a different criterion, but it is hard to do this correctly.
Also, even if you come up with a criterion that looks good now, what will you do if it starts to look worse later? For instance, maybe China at first looks like they would do conventional war, so you create a criterion based on this (say, based on the number of Chinese ships attacking Taiwan), but then later it looks like they will fire a nuke; what happens to your conditional market then?
With latent variables: You can use a latent variable to define war between China and Taiwan. This already solves part of the issue, as it deals with the measurement error and abstraction described in the previous sections.
But further, if the type of attack that China is likely to do on Taiwan changes, then the market for the latent variable will automatically update the criteria for the latent variable, and therefore you get automatic updates in the condition for the Taiwan market. People who make bets on the conditional market will also have more opportunity to notice that something fundamental has changed, because the parameters of the latent markets will have changed accordingly.
Summary of markets conditional on latents
So as usual, prediction markets require you to specify objective criteria, which may be excessively narrow. This problem is compounded when you do conditional markets: you have to specify objective criteria not just for the outcome, but also for the condition in which the market should apply. Further, if things change so the condition is no longer relevant, you often have no way of changing the condition.
Latent variables assist with this. First, a latent variable can be used to adjust for measurement error or abstract criteria to be more generally applicable, as described in the previous section. But second, if things change so the previous condition no longer applies, latent variables will automatically update to address new conditions.
Technical guide
Prerequisites: This guide assumes that you are comfortable with probability theory, prediction markets and calculus. It also does not go into very much detail in describing what latent variables are, so I hope you got an intuition for them in the previous text.
In their simplest incarnation, reflective latent variables are a way of factoring a joint probability distribution P(X0,X1,…,Xn). Here, X0,X1,…,Xn are known as the indicators of the latent variable, and in prediction markets they would be the concrete markets such as "Will Ukraine have control over Crimea by the end of 2023?" that have been mentioned above. If you are familiar with Bayesian networks, reflective latent variables correspond to the following Bayesian network:
Mathematically, the latent variable works by "pretending" that we have a new variable Y, and that the joint probability distribution can be factorized as
P(X0,X1,…,Xn)=∫YP(Y)∏iP(Xi|Y)[3]
If Y is a discrete latent variable, the integral would be a sum.
A probability distribution like P(X0,X1,…,Xn) in principle has exponentially many degrees of freedom (one degree of freedom for each combination of the Xs), whereas a latent variable model factorizes it into having linearly many degrees of freedom (a constant amount of degrees of freedom for P(Y), plus a linear amount of degrees of freedom for P(Xi|Y)). I think this makes it feasible for users of a prediction market to get an overview of and make predictions on the latent variable.
Types of latent variables
The main distinction between different kinds of latent variable models is whether Xi and Y are continuous or discrete. This affects the models that can be used for P(Y) and P(Xi|Y), which has big implications for the use of the models. There are four commonly used types of latent variable models, based on this consideration:
It seems like a prediction market should support both continuous and discrete indicators for latent variable models. Luckily, it is perfectly mathematically possible to mix and match, such that some indicators are treated as discrete (as implied by IRT and LCA), while other indicators are treated as continuous (as implied by FA and MM). This just requires a bit of a custom model, but I don't think it seriously complicates the math, so that is not a big concern.
Rather, the important distinction is between models where the latent variable is continuous, versus models where the latent variable is discrete. Since there is only one latent variable in a given latent variable market, one cannot simply mix and match.[4] Basically, the different between the two kinds of markets are:
I think one benefit of LCA/MM is that it is likely much more intuitive to users. Sketching out different abstract scenarios seems like the standard way for people to make predictions. However, I think some benefits of IRT/FA are that many phenomena have an inherent continuity to them, as well as that they are more likely to update naturally with new evidence, and require fewer parameters. More on that in the Design section.
Implementation for item response theory
My implementation of latent variable markets used item response theory, so it is item response theory that I have most thoroughly thought through the math for. I think a lot of the concrete math might generalize to other cases, but also a lot might not.
Item response theory has two components:
In terms of parameters, the most straightforward way we could parameterize the IRT model is with 2+2n parameters:
This is not the only representation that can be used, and it is not the one I used behind the scenes in my implementation. However, it is a useful representation for understanding the probability theory, and it can often be useful to switch to different representations to make the coding simpler.
Betting: In order to make a bet, one can change the parameters (μY, σY, →ai, →bi) of the market. I support several different types of bets in my implementation, because there are several different types of information people might want to add to the market.
A big part of the value in latent variable markets is in the ability to change the latent distribution (μY,σY) to some new distribution (μ′Y,σ′Y). For instance, if one has observed some information that narrows down the range of plausible outcomes, one might want to change the distribution to a narrower one, such as(μ′Y,σ′Y)=(μY+x,σY−x). (In my mockup I implemented this via buttons, but for a nice UI one could probably let people freely drag around the latent variable distribution, rather than dealing with clunky buttons. See the "Design decisions" section for more.)
Another type of bet that people could make is a conditional bet, changing (ai,bi) to update the relationship between the latent variable and the outcome of interest. However, I think the nature of the (ai,bi) parameters might be counterintuitive because they are quite abstract, so I instead did a change of variables to (o+2,i,o−2,i)=(2ai+bi,−2ai+bi), with (o+2,i,o−2,i) representing the logits for the outcome when the latent variable is high and low respectively. Furthermore I converted them back to probabilities in the interface to make them more interpretable to users.
Scoring bets: The betting interface described above gives a way for people's bets to change the parameters of the market. However, that requires a scoring rule in order to give people incentives to select good parameters. I used the log scoring rule in order to give people payoffs.
That is, if you change the parameters (μY, σY, →ai, →bi) from ϕ to θ, and the markets resolved to →X, you would get a score and a net payout of logP(→X|θ)−logP(→X|ϕ).
To ensure that the payout is always positive (perhaps more relevant for Manifold than Metaculus), I split this score up in two steps. When performing the bid, you pay max→QlogP(→Q|ϕ)−logP(→Q|θ). Then when the market resolves, you get a payout of logP(→X|θ)−logP(→X|ϕ)+max→QlogP(→Q|ϕ)−logP(→Q|θ).
When you expand out P(→X|ψ), you get a nasty integral. I solved this integral numerically.
Integration with existing markets: The math that handles latent variables includes certain parameters (μY, σY, →ai, →bi). However, these are not necessarily the parameters we want to store in the database of the prediction market. For one, (μY, σY, →ai, →bi) are redundant and can be simplified. But for two, the prediction market already stores certain parameters in the database (P(Xi)), and it would be nice if we could keep those, to Make Illegal States Unrepresentable.
So we want to find some set of parameters to add to the database, next to P(Xi), which are equivalent in expressive power to (μY, σY, →ai, →bi).
First, the parameters μY and σY can be eliminated by changing P(Y) to a standard Gaussian distribution (i.e. with μ=0 and σ=1) and transforming a′i=aiσY, and b′i=bi+aiμY.
Now we have 2n parameters. Given these 2n parameters, we can use a constraint to eliminate the b′is, namely:
P(Xi)=∫11+e−a′iY−b′iP(Y)dY
I don't know of a closed form for solving the above equation for b′i, so I cheated. Rather than using a logistic curve P(X|Y=y)=11+e−ay−b, we can use a probit curve P(X|Y=y)=Φ(ay+b), where Φ is the CDF for the unit normal distribution. Φ has a similar shape to the logistic sigmoid function, but it more rapidly goes to 0 and 1 in the tails.
Importantly, we can rephrase the probit model to P(X|Y=y)=P(ay+b+ε>0), for ε∼N(0,1). Then we can scale ay+b+ε down by a factor of √a2+1, which preserves the probability that the expression exceeds 0. However, importantly, by scaling it down, it means that if we marginalize over Y (and Y has a unit normal distribution), then aY+ε√a2+1 will have a unit normal distribution, and so:
P(X)=P(aY+b+ε>0)=P(b√a2+1+aY+ε√a2+1>0)=P(b√a2+1+ε>0)=Φ(b√a2+1)
Or in other words, b=Φ−1(P(X))√a2+1.
(In my actual implementation, I then cheated some more to switch back to a logit model, but that was mainly because I didn't want to code up Φ and Φ−1 in Javascript. I suspect that using a probit model instead of a logit model is the best solution.)
To recap, if the database for the market just stores P(Xi) and a′i, we can recover b′i=Φ−1(P(Xi))√a′i2+1, μY=0, σY=1.
(In my implementation I did two further changes. First, I shifted μY and σY to better represent the distribution of logits implied by the market, in order to make the market history more meaningful. I think something like this is probably a good idea for implementing latent variable markets in practice, but my implementation was fairly simplistic. Secondly, rather than storing a′i, I stored λi=a′i√a′i2+1, called the standardized loading, which is essentially the correlation between the latent variable and the observed variable, and so takes values in the interval (−1,1).)
Signal to noise ratio: At the bottom of my market, I plot what I call the "signal:noise ratio" of the market. It looks like this:
It might be kind of confusing, so let me explain. The key to understanding how to think about this is to consider how things look after all the markets resolve.
Without loss of generality, assume that all the markets had a positive ai, so that a YES resolution aligns with the latent variable being higher, and a NO resolution aligns with the latent variable being lower. (If any of the markets instead had a negative ai, we can invert the resolution criterion for that market to give it a positive ai.)
Consider the amount of indicator markets which resolved yes, which I will call ^Y. This amount will presumably be highly correlated with the "true" value of Y. (That is, the number of YES-resolving markets about how whether Ukraine has done well in the war will be a good indicator of whether Ukraine has done well in the war.) But we should also expect there to be some noise, due to random distinctions between the resolution criteria and the latent variables.
The signal:noise ratio measures the amount of correlation between ^Y and Y, relative to the amount of noise in ^Y that is unrelated to Y. More specifically, for a given level y of Y, we can use the market parameters to compute s(y)=ddyE[^Y|Y=y], representing the signal or sensitivity to the true level of Y, as well as compute n(y)=StDev[^Y|Y=y], representing the amount of noise in the market resolution. The signal-to-noise ratio then plots s(y)n(y) as a function of y.
More formally, we have ^Y=∑iXi. We can then derive s(y) by:
s(y)=ddyE[^Y|Y=y]=∑iddyP[Xi|Y=y]=∑iddy11+e−aiy−bi=∑iai(11+e−aiy−bi)2
(assuming we use a logistic model; if we instead use a probit model, a different derivation would be used)
To derive n(y), we can make use of the fact that the variance of independent variables commutes with sums, and that the Bernoulli distribution with probability p has variance p(1−p) to compute:
n(y)2=Var(^Y|Y=y)=∑iVar[Xi|Y=y]=∑i1(1+e−aiy−bi)(1+eaiy+bi)
So then overall, the signal-to-noise ratio for the market is:
f(y)=∑iai(11+e−aiy−bi)2√∑i1(1+e−aiy−bi)(1+eaiy+bi)
I expect that it will generally be considered good practice to ensure that the signal-to-noise ratio is reasonably high (maybe 1.0 or more), so that the bets are not too noisy. One of the advantages of latent variable markets is that they provide a mechanism to reach agreement on the signal-to-noise ratio ahead of market resolution, by using formulas like this. One can then improve the signal-to-noise ratio by creating more indicator markets covering more aspects of the outcome in question. Asymptotically, the signal-to-noise ratio goes at roughly O(√n) where n is the number of indicator markets.
(If you want to look up more about this in the literature, the keyword to search for is "test information function". That said, when working with test information functions, usually people work with other ways of quantifying things than I am doing here, so it doesn't translate directly.)
Basics of latent class models
The above gives the guts of my implementation of item response theory. However, this is not the only possible latent variable model, so I thought I should give some information about another kind of model too, called latent class models. This won't be as comprehensive because I haven't actually implemented it for prediction markets and so there might be random practical considerations that come up which I won't explain here.
In a latent class model, Y takes value in a fixed set of k classes, which for the purposes of this section I will treat as numbers Y∈{0,1,…,k−1}, but remember that semantically these classes are not simply numbers but might be assigned high-level meanings such as "AI FOOM" or "Ukraine kicks Russia out of its territory".
A latent class model has two kinds of parameters:
Like with the item response theory model, the latent class model could use log scoring in order to incentivize predictions, which requires us to have a formula for the probability of an outcome given the market parameters. This formula is:
P(→Xi)=∑jpj∏iXiqi,j+(1−Xi)(1−qi,j)
Design decisions
While thinking about and developing latent variable markets, I've also come with some thoughts for the design tradeoffs that can be made. I thought I might as well drop some of them here. Obviously these are up for reevaluation, but they would probably be a good starting point.
Types of latent variable markets
As mentioned before, there are multiple types of latent variable models, e.g.:
Since prediction markets typically support both discrete and continuous markets, it seems logical that there should be support for both discrete and continuous indicators.
Ideally there should also be support for both discrete and continuous latents, but it might be nice to get a better understanding for the tradeoffs.
Who chooses the number of outcomes for the discrete latent?
A discrete latent variable requires some set of outcomes, which someone has to choose. Maybe the person creating the latent variable market should choose them? For instance, maybe someone creating a latent variable market on the Ukraine war might choose two outcomes, which they label as "Ukraine wins" and "Russia wins"?
But what if a predictor thinks that it will end in a stalemate? If they were restricted to "Ukraine wins" and "Russia wins" as options, they would have to co-opt one of those to represent the stalemate outcome.
This can be fixed simply enough by letting everyone propose new outcomes. But that raises the question of how letting everyone propose new outcomes should be handled in the UI:
This is part of what makes me disprefer discrete latent variable markets. If there was a solution to this, maybe discrete latent variable markets would be superior to continuous ones.
Other assorted thoughts
Latent variable markets vs combinatorial markets
Latent variable markets aren't the only prediction market extension people have considered. The most general approach would be to allow people to make bets using arbitrary Bayesian networks, a concept called combinatorial prediction markets.
Bayesian networks support latent variables, and so allowing general Bayesian networks can be considered a strict generalization of allowing latent variables, as long as one remembers to support latent variable in the Bayesian network implementation.
In principle I love the idea of combinatorial prediction markets, but I think it makes the interface much more complex, and I think a large chunk of the value would be provided by the relatively simpler notion of latent variables, so unless there's rapid plans in the works to implement fully combinatorial prediction markets, I would recommend focusing primarily on latent variable markets.
Furthermore, insofar as we consider latent variable markets desirable for reducing measurement error, we might prefer conditional markets to always be conditional on a latent variable market, rather than a simple objective criteria. So when applying creating Bayesian networks to link different markets, it might make sense to favor linking latent variables to each other, rather than working with object-level markets. (In psychology, this is the distinction between a measurement model and the structural model.) If so, one can think of latent variable markets as being a "first step" towards more general combinatorial markets.
Number of indicator markets
When working with latent variable models, I tend to think that one should require at least 3 indicators. The reason is that the latent variable is underdetermined by 2 indicators. For instance, you could either have X0=Y, and therefore have P(X1|Y)=P(X1|X0). Or vice versa. Essentially, what goes wrong is that if X0 and X1 are imperfectly correlated with each other, then there is no rule for deciding which one is "more correlated" with Y, the latent variable.
However, more generally, it is advisable to have a bunch of indicators. When you have only a few indicators, it is quite subjective what the "true value" of the latent variable should be. But as you add more and more indicators, it gets pinned down better and better.
Creating latent variable markets
When creating latent variable markets, it seems like it would be advisable to create an option to include preexisting indicator markets into the latent variable, to piggyback off their efforts.
However, since it is valuable to have many indicators for latent variable markets, maybe the interface for creating latent variable markets should also support creating new associated indicator markets together with the latent variable market, in a quick and easy way.
Adding new indicators to markets
As a latent variable market is underway, new questions will arise, and old questions will be resolved. It seems to me that there's no reason not to just allow people to add questions to the latent variable markets
Multifactor latent variable models
Continuous latent variable models typically support having the latent variable Y be a vector →Y. This means that rather than having P(Xi|Y)=f(aiY+bi), you would have P(Xi|Y)=f(→ai⋅→Y+bi) for vector-valued ai.
I think multifactor latent variable models would be appealing as they can better model things of interest. For instance in the Ukraine war, there is not just the axis of whether Ukraine or Russia will win, but also the (orthogonal?) axis of how far the war will escalate - the nukes vs treaty axis.
I would recommend allowing multidimensionality in latent variable markets, except I don't know of any nice interfaces for supporting this. When I've worked with multidimensional latent variables, it has usually been with computer libraries that computed them for me. Manually fitting multidimensional latent variables sounds like a pain.
Selling bets on latent variable markets
On ordinary markets, if you've bought some shares, you can sell them again:
I don't know of a neat way to achieve this with latent variable markets. So I guess it won't be supported?
I'm not sure how big of a problem that would be.
If you changed your mind quickly enough for the market to not have moved much, you could buy shares in the opposite direction to offset your mistake. This would still mean that you have your money tied up in the market. (On Manifold Markets, that seems like no big deal because of the loan system. On Metaculus, that seems like no big deal because you don't have a fixed pool of money but instead a point system for predictions.)
If the market moves a lot, then you might not have any reasonable way to buy shares to offset your mistake without making overconfident predictions in the opposite direction too. But really that's just how prediction markets work in general, so again that doesn't seem like a big deal.
Offers
If anyone is interested in implementing latent variable markets, I offer free guidance.
I'm aware that Manifold Markets is open-source, and I've considered implementing latent variable markets in it. However, I don't have time to familiarize myself with a new codebase right now. That said, I am 100% willing to offer free snippets of code to handle the core of the implementation.
I am also willing to pay up to $10k for various things that might help get latent variable markets implemented.
Thanks to Justis Mills for providing proofreading and feedback.
Latent variables are approximately equivalent to PCA, and PCA is good for dimension-reduction (finding the most important axes of variation). So if you have a large, wildly varied pool of questions, you could throw a latent variable market at it to have people bet about what the most important uncertainty in this pool is. But that might be too complicated to apply in practice.
I think latent variable markets could also help deal with "missing data" or N/A resolutions? That is, suppose you want to make a prediction market about the future, but you can't think of any good criterion which won't have a significant chance of resolving N/A. In that case, you could use a bunch of different criteria that resolve as N/A under different conditions, and the latent variable market could allow you to see the overall pattern.
Or in less dense and more unambiguous but less elegant notation:
P(X0=x0,X1=x1,…,Xn=xn)=∫y(∏iP(Xi=xi|Y=y))p(Y=y)dy
This is not strictly 100% true, there are some more elaborate cases where one can combine them, but it doesn't seem worth the complexity to me.