2 Answers sorted by
70
I think it's important to remind yourself what the latent vs observable variables represent.
The observable variables are, well, the observables: sights, sounds, smells, touches, etc.. Meanwhile, the latents are all concepts we have that aren't directly observable, which yes includes intangibles like friendship, but also includes high-level objects like chairs and apples, or low-level objects like atoms.
One reason to mention this is because it has implications for your graphs. The causal graph would more look like this:
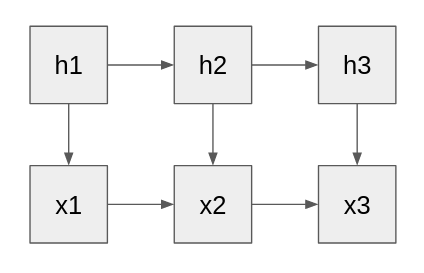
(As the graphs for HMMs tend to look. Arguably the sideways arrows for the xs are not needed, but I put them in anyway.)
Of course, that's not to say that you can't factor the probability distribution as you did, it just seems more accurate to call it something other than causal graph. Maybe inferential graph? (I suppose you could call your original graph as causal graph of people's psychology. But then the hs would only represent people's estimates of their latent variables, which they would claim could differ from their "actual" latent variables, if e.g. they were mistaken.)
Anyway, much more importantly, I think this distinction also answers your question about path-dependence. There'd be lots of path-dependence, and it would not be undesirable to have the path-dependence. For example:
- If you observe that you get put into a simulation, but the simulation otherwise appears realistic, then you have path-dependence because you still know that there is an "outside the simulation".
- If you observe that an apple in your house, then you update your estimate of h to contain that apple. If you then leave your house, then x no longer shows the apple, but you keep believing in it, even though you wouldn't believe it if your original observation of your house had not found an apple.
- If you get told that someone is celebrating their birthday tomorrow, then tomorrow you will believe that they are celebrating their birthday, even if you aren't present there.
I think you misunderstood my graph - the way I drew it was intentional, not a mistake. Probably I wasn't explicit enough about how I was splitting the variables and what I do is somewhat different from what johnswentworth does, so let me explain.
Some latent variables could have causal explanatory power, but I'm focusing on ones that don't seem to have any such power because they are the ones human values depend on most strongly. For example, anything to do with qualia is not going to have any causal arrows going from it to what we can observe, but neverthe...
30
Here's a partial answer to the question:
It seems like one common and useful type of abstraction is aggregating together distinct things with similar effects. Some examples:
- "Heat" can be seen as the aggregation of molecular motion in all sorts of directions; because of chaos, the different directions and different molecules don't really matter, and therefore we can usefully just add up all their kinetic energies into a variable called "heat".
- A species like "humans" can be seen as the aggregation (though disjunction rather than sum) of many distinct genetic patterns. However, ultimately the genetic patterns are simple enough that they all code for basically the same thing.
- A person like me can be seen as the aggregation of my state through my entire life trajectory. (Again unlike heat, this would be disjunction rather than sum.) A major part of why the abstraction of "tailcalled" makes sense is that I am causally somewhat consistent across my life trajectory.
An abstraction that aggregates distinct things with similar effects seems like it has a reasonably good chance to be un-path-dependent. However, it's not quite guaranteed, which you can see by e.g. the third example. While I will have broadly similar effects through my life trajectory, the effects I will have will change over time, and the way they change may depend on what happens to me. For instance if my brain got destructively scanned and uploaded while my body was left behind, then my effects would be "split", with my psychology continuing into the upload while my appearance stayed with my dead body (until it decayed).
"Heat" can be seen as the aggregation of molecular motion in all sorts of directions; because of chaos, the different directions and different molecules don't really matter, and therefore we can usefully just add up all their kinetic energies into a variable called "heat".
Nitpick: this is not strictly correct. This would be the internal energy of a thermodynamic system, but "heat" in thermodynamics refers to energy that's exchanged between systems, not energy that's in a system.
Aside from the nitpick, however, point taken.
...An abstraction that aggregate
In the Pointers Problem, John Wentworth points out that human values are a function of latent variables in the world models of humans.
My question is about a specific kind of latent variable, one that's restricted to be downstream of what we can observe in terms of causality. Suppose we take a world model in the form of a causal network and we split variables into ones that are upstream of observable variables (in the sense that there's some directed path going from the variable to something we can observe) and ones that aren't. Say that the variables that have no causal impact on what is observed are "latent" for the purposes of this post. In other words, latent variables are in some sense "epiphenomenal". This definition of "latent" is more narrow but I think the distinction between causally relevant and causally irrelevant hidden variables is quite important, and I'll only be focusing on the latter for this question.
In principle, we can always unroll any latent variable model into a path-dependent model with no hidden variables. For example, if we have an (inverted) hidden Markov model with one observable xk and one hidden state hk (subscripts denote time), we can draw a causal graph like this for the "true model" of the world (not the human's world model, but the "correct model" which characterizes what happens to the variables the human can observe):
Here the hk are causally irrelevant latent variables - they have no impact on the state of the world xk but for some reason or another humans care about what they are. For example, if a sufficiently high capacity model renders "pain" a causally obsolete concept, then pain would qualify as a latent variable in the context of this model.
The latent variable hk at time k depends directly on both xk and hk−1, so to accurately figure out the probability distribution of hk we need to know the whole trajectory of the world from the initial time: x1,x2,…,xk.
We can imagine, however, that even if human values depend on latent variables, these variables don't feed back into each other. In this case, how much we value some state of the world would just be a function of that state of the world itself - we'd only need to know xk to figure out what hk is. This naturally raises the question I ask in the title: empirically, what do we know about the role of path-dependence in human values?
I think path-dependence comes up often in how humans handle the problem of identity. For example, if it were possible to clone a person perfectly and then remove the original from existence through whatever means, even if the resulting states of the world were identical, humans who have different trajectories of how we got there in their mental model could evaluate questions of identity in the present differently. Whether I'm me or not depends on more information than my current physical state or even the world's current physical state.
This looks like it's important for purposes of alignment because there's a natural sense in which path-dependence is an undesirable property to have in your model of the world. If an AI doesn't have that as an internal concept, it could be simpler for it to learn a strategy of "trick the people who believe in path-dependence into thinking the history that got us here was good" rather than "actually try to optimize for whatever their values are".
With all that said, I'm interested in what other people think about this question. To what extent are human values path-dependent, and to what extent do you think they should be path-dependent? Both general thoughts & comments and concrete examples of situations where humans care about path-dependence are welcome.