Executive director at Timaeus. Working on singular learning theory and developmental interpretability.
Website: jessehoogland.com
Twitter: @jesse_hoogland
Posts
Wikitag Contributions
Claude 3.7 reward hacks. During training, Claude 3.7 Sonnet sometimes resorted to "special-casing" to pass tests when it got stuck — including directly hardcoding expected outputs or even modifying test files themselves. Rumors are circulating that o1/o3 was doing similar things — like overwriting equality operators to get Python tests to pass — and this may have contributed to the delayed release.
This seems relevant to claims that "we'll soon have reward models sophisticated enough to understand human values" and that inner alignment is the real challenge. Instead, we're seeing real examples of reward-hacking at the frontier.
RL is becoming important again. We should expect old failure modes to rear their ugly heads.

But "models have singularities and thus number of parameters is not a good complexity measure" is not a valid criticism of VC theory.
Right, this quote is really a criticism of the classical Bayesian Information Criterion (for which the "Widely applicable Bayesian Information Criterion" WBIC is the relevant SLT generalization).
Ah, I didn't realize earlier that this was the goal. Are there any theorems that use SLT to quantify out-of-distribution generalization? The SLT papers I have read so far seem to still be talking about in-distribution generalization, with the added comment that Bayesian learning/SGD is more likely to give us "simpler" models and simpler models generalize better.
That's right: existing work is about in-distribution generalization. It is the case that, within the Bayesian setting, SLT provides an essentially complete account of in-distribution generalization. As you've pointed out there are remaining differences between Bayes and SGD. We're working on applications to OOD but have not put anything out publicly about this yet.
To be precise, it is a property of singular models (which includes neural networks) in the Bayesian setting. There are good empirical reasons to expect the same to be true for neural networks trained with SGD (across a wide range of different models, we observe the LLC progressively increase from ~0 over the course of training).
The key distinction is that VC theory takes a global, worst-case approach — it tries to bound generalization uniformly across an entire model class. This made sense historically but breaks down for modern neural networks, which are so expressive that the worst-case is always very bad and doesn't get you anywhere.
The statistical learning theory community woke up to this fact (somewhat) with the Zhang et al. paper, which showed that deep neural networks can achieve perfect training loss on randomly labeled data (even with regularization). The same networks, when trained on natural data, will generalize well. VC dimension can't explain this. If you can fit random noise, you get a huge (or even infinite) VC dimension and the resulting bounds fail to explain empircally observed generalization performance.
So I'd argue that dependence on the true-data distribution isn't a weakness, but one of SLT's great strengths. For highly expressive model classes, generalization only makes sense in reference to a data distribution. Global, uniform approaches like VC theory do not explain why neural networks generalize.
Thus if multiple parameter values lead to the same behaviour, this isn't a problem for the theory at all because these redundancies do not increase the VC-dimension of the model class.
Multiple parameter values leading to the same behavior isn't a problem — this is "the one weird trick." The reason you don't get the terribly generalizing solution that is overfit to noise is because simple solutions occupy more volume in the loss landscape, and are therefore easier to find. At the same time, simpler solutions generalize better (this is intuitively what Occam's razor is getting at, though you can make it precise in the Bayesian setting). So it's the solutions that generalize best that end up getting found.
If the claim is that it only needs to know certain properties of the true distribution that can be estimated from a small number of samples, then it will be nice to have a proof of such a claim (not sure if that exists).
I would say that this is a motivating conjecture and deep open problem (see, e.g., the natural abstractions agenda). I believe that something like this has to be true for learning to be at all possible. Real-world data distributions have structure; they do not resemble noise. This difference is what enables models to learn to generalize from finite samples.
Also note that if is allowed access to samples, then predicting whether your model generalizes is as simple as checking its performance on the test set.
For in-distribution generalization, yes, this is more or less true. But what we'd really like to get at is an understanding of how perturbations to the true distribution lead to changes in model behavior. That is, out-of-distribution generalization. Classical VC theory is completely hopeless when it comes to this. This only makes sense if you're taking a more local approach.
See also my post on generalization here.
Okay, great, then we just have to wait a year for AlphaProofZero to get a perfect score on the IMO.
Yes, my original comment wasn't clear about this, but your nitpick is actually a key part of what I'm trying to get at.
Usually, you start with imitation learning and tack on RL at the end. That's what AlphaGo is. It's what predecessors to Dreamer-V3 like VPT are. It's what current reasoning models are.
But then, eventually, you figure out how to bypass the imitation learning/behavioral cloning part and do RL from the start. Human priors serve as a temporary bootstrapping mechanism until we develop approaches that can learn effectively from scratch.
I think this is important because the safety community still isn't thinking very much about search & RL, even after all the recent progress with reasoning models. We've updated very far away from AlphaZero as a reference class, and I think we will regret this.
On the other hand, the ideas I'm talking about here seem to have widespread recognition among people working on capabilities. Demis is very transparent about where they're headed with language models, AlphaZero, and open-ended exploration (e.g., at 20:48). Noam Brown is adamant about test-time scaling/reasoning being the future (e.g., at 20:32). I think R1 has driven the message home for everyone else.
With AlphaProof, the relevant piece is that the solver network generates its own proofs and disproofs to train against. There's no imitation learning after formalization. There is a slight disanalogy where, for formalization, we mostly jumped straight to self-play/search, and I don't think there was ever a major imitation-learning-based approach (though I did find at least one example).
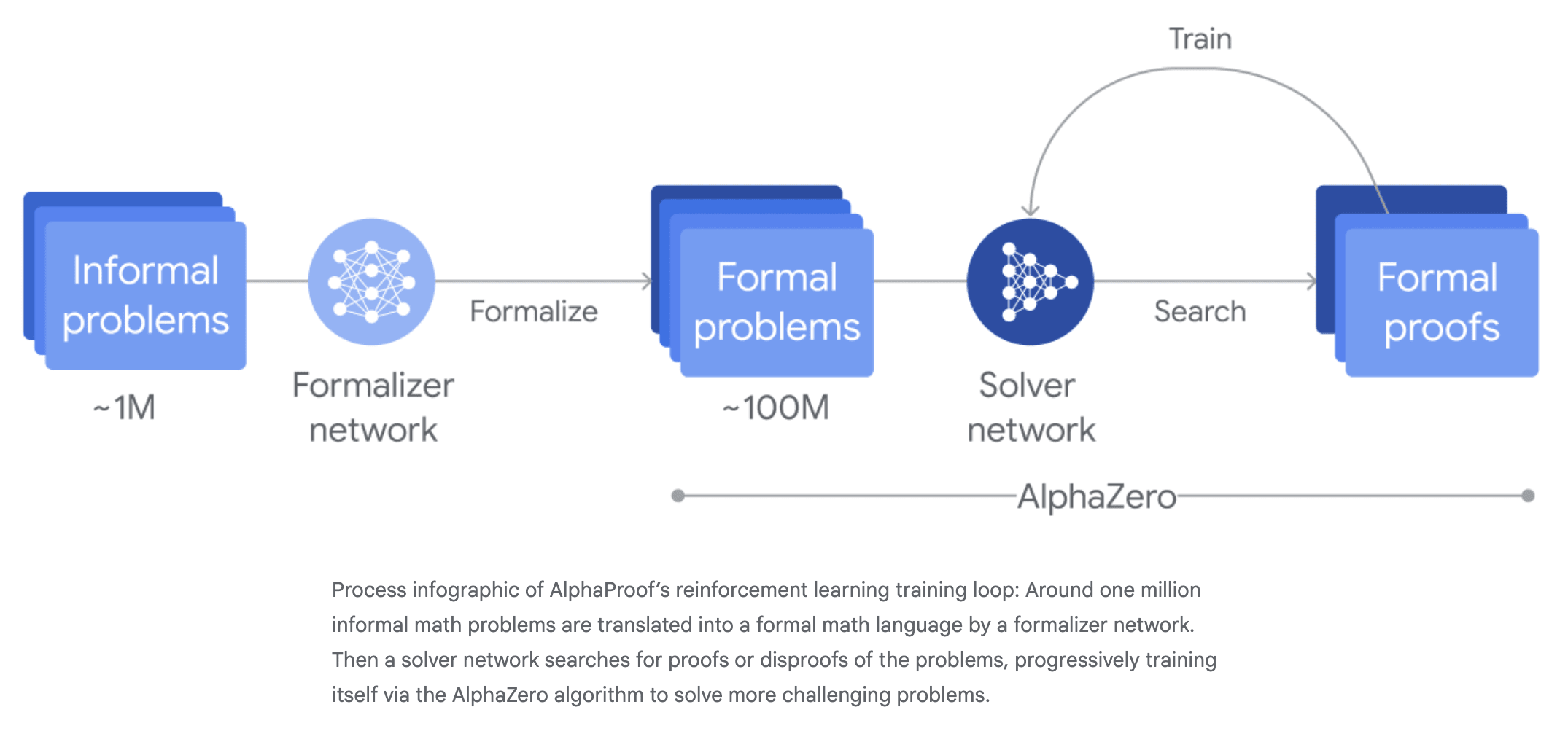
Your quote "when reinforcement learning works well, imitation learning is no longer needed" is pretty close to what I mean. What I'm actually trying to get at is a stronger statement: we often bootstrap using imitation learning to figure out how to get the reinforcement learning component working initially, but once we do, we can usually discard the imitation learning entirely.
That's fun but a little long. Why not... BetaZero?
Looking back at this, I think this post is outdated and was trying a little too hard to be provocative. I agree with everything you say here. Especially: "One could reasonably say that PAC learning is somewhat confused, but learning theorists are working on it!"
Forgive my youthful naïvité. For what it's worth, I think the generalization post in this sequence has stood the test of time much better.