Posts
Wikitag Contributions
Yes that's right (regardless of whether it's resolute or whether it's using 'strong' maximality).
A sort of of a decision tree where the agent isn't representable as having complete preferences is the one you provide here. We can even put the dynamic aspect aside to make the point. Suppose that the agent is fact inclined to pick A+ over A, but doesn't favour or disfavour B to either one. Here's my representation: maximal choice with A+ A and B A,A+. As a result, I will correctly predict its behaviour: it'll choose something other than A.
Can I also do this with another representation, using a complete preference relation? Let's try out indifference between A+ and B. I'd indeed make the same prediction in this particular case. But suppose the agent were next to face a choice between A+, B, and B+ (where the latter is a sweetening of B). By transitivity, we know B+ A+, and so this representation would predict that B+ would be chosen for sure. But this is wrong, since in fact the agent is not inclined to favour B-type prospects over A-type prospects. In contrast, the incomplete representation doesn't make this error.
Summing up: the incomplete representation works for {A+,A,B} and {A+,B,B+} while the only complete one that also works for the former fails for the latter.
Thanks. Let me end with three comments. First, I wrote a few brief notes here that I hope clarify how Independence and IIA differ. Second, I want to stress that the problem with the use of Dutch books in the articles is a substantial one, not just a verbal one, as I explained here and here. Finally, I’m happy to hash out any remaining issues via direct message if you’d like—whether it’s about these points, others I raised in my initial comment, or any related edits.
I don't apprecaite the hostility. I aimed to be helpful in spending time documenting and explaining these errors. This is something a heathy epistemic community is appreciative of, not annoyed by. If I had added mistaken passages to Wikipedia, I'd want to be told, and I'd react by reversing them myself. If any points I mentioned weren't added by you, then as I wrote in my first comment:
...let me know that some of the issues I mention were already on Wikipedia beforehand. I’d be happy to try to edit those.
The point of writing about the mistakes here is to make clear why they indeed are mistakes, so that they aren't repeated. That has value. And although I don't think we should encourage a norm that those who observe and report a problem are responsible for fixing it, I will try to find and fix at least the pre-existing errors.
I agree that there exists the dutch book theorem, and that that one importantly relates to probabilism
I'm glad we could converge on this, because that's what I really wanted to convey.[1] I hope it's clearer now why I included these as important errors:
- The statement that the vNM axioms “apart from continuity, are often justified using the Dutch book theorems” is false since these theorems only relate to belief norms like probabilism. Changing this to 'money pump arguments' would fix it.
- There's a claim on the main Dutch book page that the arguments demonstrate that “rationality requires assigning probabilities to events [...] and having preferences that can be modeled using the von Neumann–Morgenstern axioms.” I wouldn't have said it was false if this was about money pumps.[2] I would've said there was a terminological issue if the page equated Dutch books and money pumps. But it didn't.[3] It defined a Dutch book as "a set of bets that ensures a guaranteed loss." And the theorems and arguments relating to that do not support the vNM axioms.
Would you agree?
- ^
The issue of which terms to use isn't that important to me in this case, but let me speculate about something. If you hear domain experts go back and forth between 'Dutch books' and 'money pumps', I think that is likely either because they are thinking of the former as a special case of the latter without saying so explicitly, or because they're listing off various related ideas. If that's not why, then they may just be mistaken. After all, a Dutch book is named that way because a bookie is involved!
- ^
Setting asside that "demonstrates" is too strong even then.
- ^
It looks like OP edited the page just today and added 'or money pump'. But the text that follows still describes a Dutch book, i.e. a set of bets. (Other things were added too that I find problematic but this footnote isn't the place to explain it.)
I think it'll be helpful to look at the object level. One argument says: if your beliefs aren't probabilistic but you bet in a way that resembles expected utility, then you're succeptible to sure loss. This forms an argument for probabilism.[1]
Another argument says: if your preferences don't satisfy certain axioms but satisfy some other conditions, then there's a sequence of choices that will leave you worse off than you started. This forms an agument for norms on preferences.
These are distinct.
These two different kinds of arguments have things in common. But they are not the same argument applied in different settings. They have different assumptions, and different conclusions. One is typically called a Dutch book argument; the other a money pump argument. The former is sometimes referred to as a special case of the latter.[2] But whatever our naming convensions, it's a special case that doesn't support the vNM axioms.
Here's why this matters. You might read assumptions of the Dutch book theorem, and find them compelling. Then you read a article telling you that this implies the vNM axioms (or constitutes an argument for them). If you believe it, you've been duped.
- ^
(More generally, Dutch books exist to support other Bayesian norms like conditionalisation.)
- ^
This distinction is standard and blurring the lines leads to confusions. It's unfortunate when dictionaries, references, or people make mistakes. More reliable would be a key book on money pumps (Gustafsson 2022) referring to a key book on Dutch books (Pettigrew 2020):
"There are also money-pump arguments for other requirements of rationality. Notably, there are money-pump arguments that rational credences satisfy the laws of probability. (See Ramsey 1931, p. 182.) These arguments are known as Dutch-book arguments. (See Lehman 1955, p. 251.) For an overview, see Pettigrew 2020." [Footnote 9.]
check the edit history yourself by just clicking on the "View History" button and then pressing the "cur" button
Great, thanks!
I hate to single out OP but those three points were added by someone with the same username (see first and second points here; third here). Those might not be entirely new but I think my original note of caution stands.
Scott Garrabrant rejects the Independence of Irrelevant Alternatives axiom
*Independence, not IIA. Wikipedia is wrong (as of today).
I appreciate the intention here but I think it would need to be done with considerable care, as I fear it may have already led to accidental vandalism of the epistemic commons. Just skimming a few of these Wikipedia pages, I’ve noticed several new errors. These can be easily spotted by domain experts but might not be obvious to casual readers.[1] I can’t know exactly which of these are due to edits from this community, but some very clearly jump out.[2]
I’ll list some examples below, but I want to stress that this list is not exhaustive. I didn’t read most parts of most related pages, and I omitted many small scattered issues. In any case, I’d like to ask whoever made any of these edits to please reverse them, and to triple check any I didn’t mention below.[3] Please feel free to respond to this if any of my points are unclear![4]
False statements
The page on Independence of Irrelevant Alternatives (IIA) claims that IIA is one of the vNM axioms, and that one of the vNM axioms “generalizes IIA to random events.”
Both are false. The similar-sounding Independence axiom of vNM is neither equivalent to, nor does it entail, IIA (and so it can’t be a generalisation). You can satisfy Independence while violating IIA. This is a not a technicality; it’s a conflation of distinct and important concepts. This is repeated in several places.
- The mathematical statement of Independence there is wrong. In the section conflating IIA and Independence, it’s defined as the requirement that
for any and any outcomes Bad, Good, and N satisfying Bad≺Good. This mistakes weak preference for strict preference. To see this, set p=1 and observe that the line now reads N≺N. (The rest of the explanation in this section is also problematic but the reasons for this are less easy to briefly spell out.) The Dutch book page states that the argument demonstrates that “rationality requires assigning probabilities to events [...] and having preferences that can be modeled using the von Neumann–Morgenstern axioms.” This is false. It is an argument for probabilistic beliefs; it implies nothing at all about preferences. And in fact, the standard proof of the Dutch book theorem assumes something like expected utility (Ramsey’s thesis).
This is a substantial error, making a very strong claim about an important topic. And it's repeated elsewhere, e.g. when stating that the vNM axioms “apart from continuity, are often justified using the Dutch book theorems.”
- The section ‘The theorem’ on the vNM page states the result using strict preference/inequality. This is a corollary of the theorem but does not entail it.
Misleading statements
- The decision theory page states that it’s “a branch of applied probability theory and analytic philosophy concerned with the theory of making decisions based on assigning probabilities to various factors and assigning numerical consequences to the outcome.” This is a poor description. Decision theorists don’t simply assume this, nor do they always conclude it—e.g. see work on ambiguity or lexicographic preferences. And besides this, decision theory is arguably more central in economics than the fields mentioned.
- The IIA article’s first sentence states that IIA is an “axiom of decision theory and economics” whereas it’s classically one of social choice theory, in particular voting. This is at least a strange omission for the context-setting sentence of the article.
- It’s stated that IIA describes “a necessary condition for rational behavior.” Maybe the individual-choice version of IIA is, but the intention here was presumably to refer to Independence. This would be a highly contentious claim though, and definitely not a formal result. It’s misleading to describe Independence as necessary for rationality.
- The vNM article states that obeying the vNM axioms implies that agents “behave as if they are maximizing the expected value of some function defined over the potential outcomes at some specified point in the future.” I’m not sure what ‘specified point in the future’ is doing there; that’s not within the framework.
- The vNM article states that “the theorem assumes nothing about the nature of the possible outcomes of the gambles.” That’s at least misleading. It assumes all possible outcomes are known, that they come with associated probabilities, and that these probabilities are fixed (e.g., ruling out the Newcomb paradox).
Besides these problems, various passages in these articles and others are unclear, lack crucial context, contain minor issues, or just look prone to leave readers with a confused impression of the topic. (This would take a while to unpack, so my many omissions should absolutely not be interpreted as green lights.) As OP wrote: these pages are a mess. But I fear the recent edits have contributed to some of this.
So, as of now, I’d strongly recommend against reading Wikipedia for these sorts of topics—even for a casual glance. A great alternative is the Stanford Encyclopedia of Philosophy, which covers most of these topics.
- ^
I checked this with others in economics and in philosophy.
- ^
E.g., the term ‘coherence theorems’ is unheard of outside of LessWrong, as is the frequency of italicisation present in some of these articles.
- ^
I would do it myself but I don’t know what the original articles said and I’d rather not have to learn the Wikipedia guidelines and re-write the various sections from scratch.
- ^
Or to let me know that some of the issues I mention were already on Wikipedia beforehand. I’d be happy to try to edit those.
Two nitpicks and a reference:
an agent’s goals might not be linearly decomposable over possible worlds due to risk-aversion
Risk aversion doesn't violate additive separability. E.g., for we always get whether (risk neutrality) or (risk aversion). Though some alternatives to expected utility, like Buchak's REU theory, can allow certain sources of risk aversion to violate separability.
when features have fixed marginal utility, rather than being substitutes
Perfect substitutes have fixed marginal utility. E.g., always has marginal utilities of 1 and 2.
I'll focus on linearly decomposable goals which can be evaluated by adding together evaluations of many separate subcomponents. More decomposable goals are simpler
There's an old literature on separability in consumer theory that's since been tied to bounded rationality. One move that's made is to grant weak separability accross goups of objects---features---to rationalise the behaviour of optimising accross groups first, and within groups second. Pretnar et al (2021) describe how this can arise from limited cognitive resources.
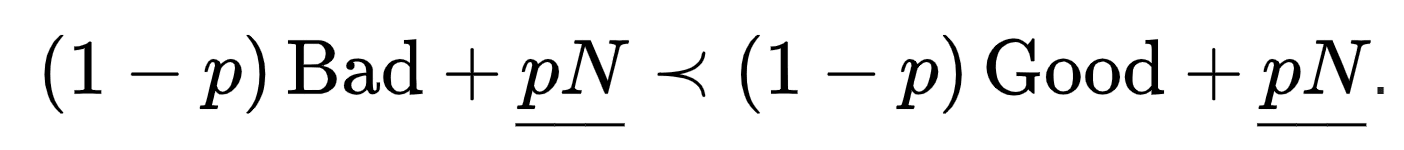
My use of 'next' need not be read temporally, though it could be. You might simply want to define a transitive preference relation for the agent over {A,A+,B,B+} in order to predict what it would choose in an arbitrary static decision problem. Only the incomplete one I described works no matter what the decision problem ends up being.
As a general point, you can always look at a decision ex post and back out different ways to rationalise it. The nontrivial task is here prediction, using features of the agent.
If we want an example of sequential choice using decision trees (rather than repeated 'de novo' choice through e.g. unawareness), it'll be a bit more cumbersome but here goes.
Intuitively, suppose the agent first picks from {A,B+} and then, in addition, from {A+,B}. It ends up with two elements from {A,A+,B,B+}. Stated within the framework:
Then (A+,x) ≻ (A,x) while (A,x) ⋈/ (B,x) for any prospect component x, and so on for other comparisons. This is how separability makes it easy to say "A+ is preferred to A" even though preferences are defined over pairs in this case. I.e., we can construct ≿ over pairs out of some ≿′ over components.
In this tree, the available prospects from the outset are (A,A+), (A,B), (B+,A+), (B+,B).
Using the same ≿′ as before, the (dynamically) maximal ones are (A,A+), (B+,A+), (B+,B).
But what if, instead of positing incomparability between A and B+ we instead said the agent was indifferent? By transitivity, we'd infer A ≻′ B and thus A+ ≻′ B. But then (B+,B) wouldn't be maximal. We'd incorrectly rule out the possibility that the agent goes for (B+,B).