Alright, I think we have an answer! The conjecture is false.

Counterexample: suppose I have a very-high-capacity information channel (N bit capacity), but it's guarded by a uniform random n-bit password. O is the password, A is an N-bit message and a guess at the n-bit password. Y is the N-bit message part of A if the password guess matches O; otherwise, Y is 0.

Let's say the password is 50 bits and the message is 1M bits. If A is independent of the password, then there's a $2^{-50}$ chance of guessing the password, so the bitrate will be about $2^{-50}$ * 1M $\approx$ $2^{-30}$, or about one-billionth of a bit in expectation.

If A "knows" the password, then the capacity is about 1M bits. So, the delta from knowing the password is a lot more than 50 bits. It's a a multiplier of $2^{50}$, rather than an addition of 50 bits.

This is really cool! It means that bits of observation can give a really ridiculously large boost to a system's optimization power. Making actions depend on observations is a potentially-very-big game, even with just a few bits of observation.

Credit to Yair Halberstadt in the comments for the attempted-counterexamples which provided stepping stones to this one.

Eliminating G

The standard definition of channel capacity makes no explicit reference to the original message $G$; it can be eliminated from the problem. We can do the same thing here, but it’s trickier. First, let’s walk through it for the standard channel capacity setup.

Standard Channel Capacity Setup

In the standard setup, $A$ cannot depend on $O$, so our graph looks like

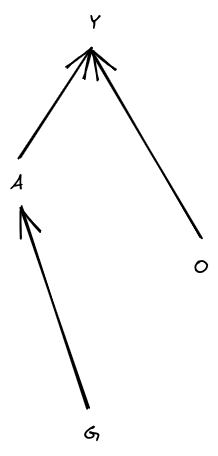
… and we can further remove $O$ entirely by absorbing it into the stochasticity of $Y$.

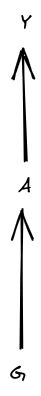
Now, there are two key steps. First step: if $A$ is not a deterministic function of $G$, then we can make $A$ a deterministic function of $G$ without reducing $I(G;Y)$. Anywhere $A$ is stochastic, we just read the random bits from some independent part of $G$ instead; $Y$ will have the same joint distribution with any parts of $G$ which $A$ was reading before, but will also potentially get some information about the newly-read bits of $G$ as well.

Second step: note from the graphical structure that $A$ mediates between $G$ and $Y$. Since $A$ is a deterministic function of $G$ and $A$ mediates between $G$ and $Y$, we have $I(G;Y)=I(A;Y)$.

Furthermore, we can achieve any distribution $P\left[A\right]$ (to arbitrary precision) by choosing a suitable function $A\left(G\right)$.

So, for the standard channel capacity problem, we have $P[G,A,Y]=P\left[G\right]P\left[A|G\right]P\left[Y|A\right]$, and we can simplify the optimization problem:

$\left({max}_{P\left[A|G\right]}I\right(G;Y\left)\right)=\left({max}_{P\left[A\right]}I\right(A;Y\left)\right)$

Note that this all applies directly to our conjecture, for the part where actions do not depend on observations.

That’s how we get the standard expression for channel capacity. It would be potentially helpful to do something similar in our problem, allowing for observation of $O$.

Our Problem

The step about determinism of $A$ carries over easily: if $A$ is not a deterministic function of $G$ and $O$, then we can change $A$ to read random bits from an independent part of $G$. That will make $A$ a deterministic function of $G$ and $O$ without reducing $I(G;Y)$.

The second step fails: $A$ does not mediate between $G$ and $Y$.

However, we can define a “Policy” variable

$\pi :=(o\mapsto A(G,o\left)\right)$

$\pi$ is also a deterministic function of $G$, and $\pi$ does mediate between G and Y. And we can achieve any distribution over policies (to arbitrary precision) by choosing a suitable function $A(G,O)$.

So, we can rewrite our problem as

$\left({max}_{P[A|G,O]}I\right(G;Y\left)\right)=\left({max}_{P\left[\pi \right]}I\right(\pi ;Y\left)\right)$

In the context of our toy example: $\pi$ has two possible values, $(o\mapsto o)$ and $(o\mapsto \overline{o})$. If $\pi$ takes the first value, then $Y$ is deterministically 0; if $\pi$ takes the second value, then $Y$ is deterministically 1. So, taking the distribution $P\left[\pi \right]$ to be 50/50 over those two values, our generalized “channel capacity” is at least 1 bit. (Note that we haven’t shown that no $P\left[\pi \right]$ achieves higher value in the maximization problem, which is why I say “at least”.)

Back to the general case: our conjecture can be expressed as

$\Delta =\left({max}_{P\left[\pi \right]}I\right(\pi ;Y\left)\right)-\left({max}_{P\left[A\right]}I\right(A;Y\left)\right)\le H\left(O\right)$

where the first optimization problem uses the factorization

$P[\pi ,O,Y]=P\left[\pi \right]P\left[O\right]P[Y|A=\pi (O),O]$

and the second optimization problem uses the factorization

$P[A,O,Y]=P\left[A\right]P\left[O\right]P[Y|A,O]$

I didn't think much about the mathematical problem, but I think that the conjecture is at least wrong in spirit, and that LLMs are good counterexample for the spirit. An LLM by its own is not very good at being an assistant, but you need pretty small amounts of optimization to steer the existing capabilities toward being a good assistant. I think about it as "the assistant was already there, with very small but not negligible probability", so in a sense "the optimization was already there", but not in a sense that is easy to capture mathematically.