Another illustrative example of the flexibility of the "market" idiom is its use in Logical Induction (summary).
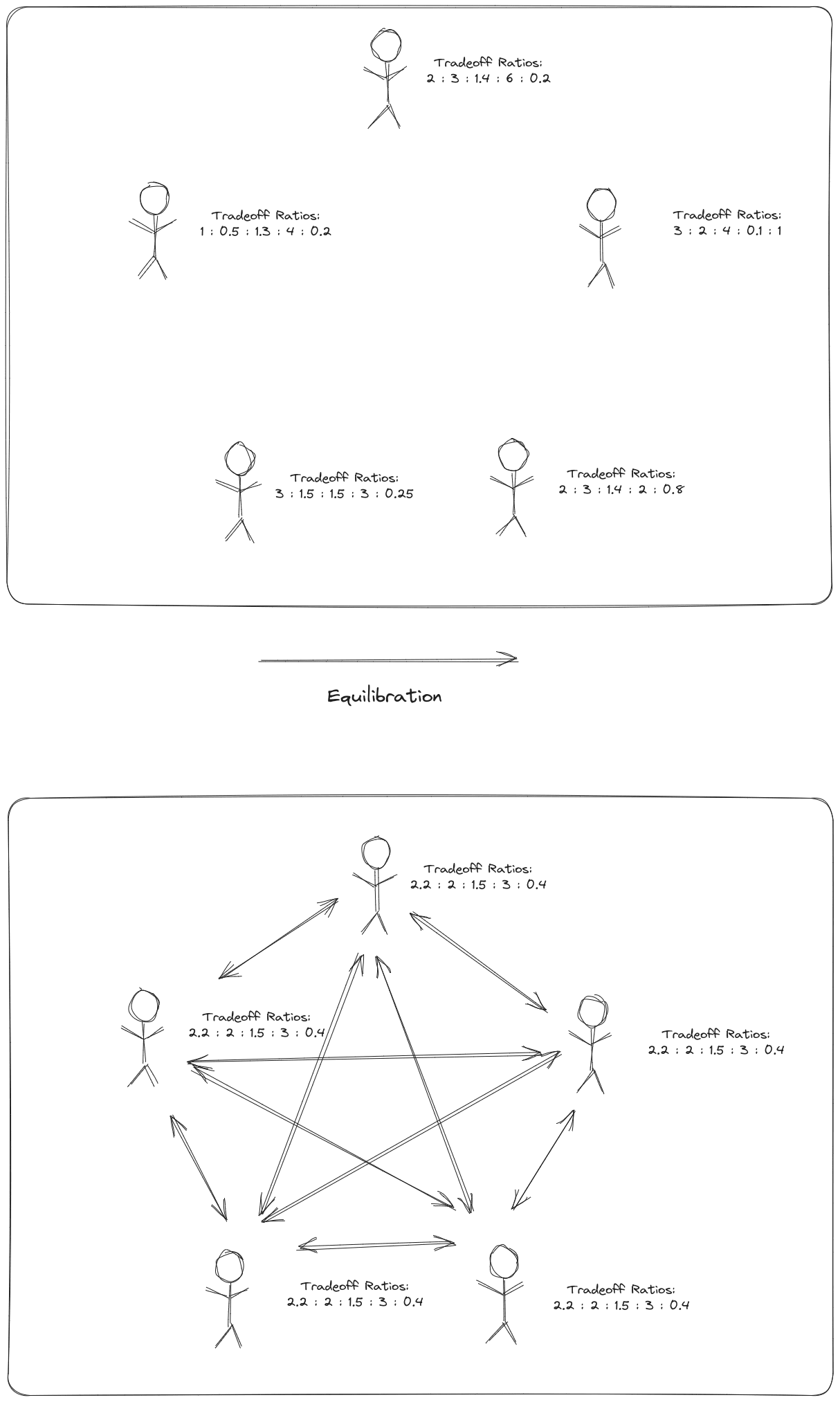
Markets can be viewed as a specific mathematical notion of "efficiency". If we have some set of functions to optimize (agent-specific utility functions or entropy to maximize, or future surprise to minimize, in the case of prediction markets) and some limited resources whose different allocations correspond to different values for this set of functions (production capacities, knowledge, compute), then saying that something is "a market" is equivalent to saying that these resources are distributed as optimally as possible, given all the resource constraints involved.
In a way, the phenomenon described by the Efficient Market Hypothesis isn't really a property of a market; it's what a market fundamentally is.
That's very interesting. I never thought about how the concepts of a market where humans trade goods can generalize to things like thermodynamics. Two thoughts though.
One is that, at least colloquially, I feel like when people talk about the term "market", it isn't implied that it is an efficient market. Like maybe some tribe of people trade amongst each other, but there are still pareto optimal trades that can be made, and so it isn't an efficient market. But we'd still call it a market.
And so secondly, I wonder is there is a better term for this sort of more general idea of market-like systems. I can't think of any and I don't particularly dislike the idea of calling them markets. Just thinking out loud.
"And that’s the core concept of a market: a bunch of subsystems at pareto optimality with respect to a bunch of goals."
The other key property is that the subsystems are able to reliably and voluntarily exchange the resources that relate to their goals. This is not always the case, especially in biological settings, because there is not always a way to enforce contracts- e.g. there needs to be a mechanism to prevent counter-parties from reneging on deals.
The anonymous referees for our paper Economic Drivers of Biological Complexity came up with this concise summary:
"Markets can arise spontaneously whenever individuals are able to engage in voluntary exchange and when
they differ in their preferences and holdings. When the individuals are people, it’s economics. When they’re
not it’s biology"
There are various ways nature overcomes the problems of contracts. One is to perform trade incrementally to gradually build trust. Alternatively, co-evolution can sometimes produce the equivalent of a secure payment system, as we discuss in our paper:
"an alternative solution to the problem of contracts is to “lock” the resource being traded in such a way that the only way to open it is to reciprocate. For example, if we view the fructose in fruit as a payment made by flora to fauna in return for seed dispersal, we see that is is very difficult (i.e. costly) for the frugivore to consume the fructose without performing the dispersal service, since it would become literally a 'sitting duck' for predators. By encapsulating the seed within the fructose, the co-evolution between frugivore and plant has resulted in the
evolution of a secure payment system".
Nope, voluntary exchange is not a key property. Indeed, the fact that we don't need that property is a key point of this post (and my older post Comparative Advantage is Not About Trade). One does need some process which tends to produce a pareto optimum, and voluntary exchange is one way that can happen, but it is certainly not the only way. So long as we have pareto optimality, we have the key properties, regardless of whether voluntary exchange is involved.
@johnswentworth ok but we can achieve Pareto optimal allocations using central planning, but one wouldn't normally call this a market?
Right, what I'd say there is that central planning when it achieves pareto optimality is behaviorally equivalent to a "market" in the sense that the post uses the term. (Indeed, it was roughly that observation which made "shadow prices" as an optimization technique such a politically-volatile topic in the USSR for a time.) Pareto optimality implies that the central planner has at least implicit prices, and behaves accordingly.
Thank you for sharing this insightful article! It was a refreshing take on economic concepts, especially the way it used the apples-and-bananas analogy. It's intriguing how these ideas extend beyond traditional economics, almost like how discussions on r/superstonk branch into unexpected territories. I appreciate the engaging read—looking forward to more thought-provoking insights!
yes if you take a particular side in the socialist calculation debate then a centrally-planned economy is isomorphic with "a market". And yes, if you ignore the Myerson–Satterthwaite theorem (and other impossibility results) then we can sweep aside the fact that most real-world "market" mechanisms do not yield Pareto-optimal allocations in practice :-)
There needs to be some variable level of exchange that can equilibriate with prices. It does not need to be euvoluntary, nor equal, nor completely free, but it needs to be SOMEHOW negotiable to find the point on the price curve.
Another way to show this is that there needs to be some competitive pressure - a tension between forces that creates/defines the equilibrium. Competition requires choice.
I suspect there's a difference in what "voluntary exchange" means in different contexts. In social contexts, it's about individual rights. In large-scale economics, it's just about the fact that the exchange curve curves downward.
@Dagon perhaps I should have place the emphasis on "transfer". The key thing is that we are able to reliably transfer ownership in exchange for renumeration and that the resource on which on goals are contingent at least needs to be excludable. If we cannot prevent arbitrary counter-parties consuming the resource in question without paying for it then we can't have a market for it.
1I don't think the emphasis should be on transfer, but on the contingency of transfer. In order for a transaction to be part of a market, as opposed to theft or other non-market transfer, the participants must have the choice NOT to make the transfer, if the exchange is not acceptable.
There are lots of variants and levels of optionality, leading to legitimate debates about "how much is this a market, vs a coerced behavior". But the core of markets and analyses of how they behave is that they are, on some scale and timeframe, voluntary.
If an arbitrary counter-party can consume the resource, this can be rephrased as destroying other agent's utility and this seems to be solved with threat-resistant ROSE values.
Not sure this is a totally correct application, though, because the consumer also gains some utility.
Checking my understanding:
If Alice and Bob have reached ideal levels of specialization, that implies they have equal marginal prices.
Alice and Bob having the same prices does not, by itself, imply they are optimally specialized. If you add in an additional assumption of non-increasing marginal returns (e.g. if doubling the amount of land devoted to apples will give you at most twice as many apples), then it implies optimality. Otherwise, Alice and Bob could be in a local maximum that is not a global maximum.
We are assuming that the marginal exchange is the same whether going upwards or downwards. This is a fairly natural assumption for a continuous system where you can make infinitesimal steps in either direction. In a discontinuous system, prices would need to be represented by something more complicated than a real number and basically you'd end up saying that Alice's and Bob's spreads of prices need to overlap, rather than that they need to be identical.
All correct?
I don't think the entropy example is a good one.
Nothing is given to the high temperature object to transfer energy to the low temperature object. So it can't be modelled as both being different agents with different tradeoffs where each agent is trying to maximize some function.
Instead I think it's a bog standard equilibrium.
Thanks for the post. I like how it gives several examples and then aims to find what's in common between them.
Recently I've been thinking that research can be seen as a kind of market where researchers specialize in research they have a comparative advantage in and trade insights by publishing and reading other researchers' work.
Economists have a very mathematically clean class of models of “markets”, and spill lots of ink arguing about how well this class of models applies to the markets of the real-world economy. I personally give relatively few shits about how well the mathematical notion of a market applies to real-world economic markets; I’m relatively more interested in applying the same models to systems in biology or ML/AI. They’re very generalizable models.
Unfortunately, the mathematical notion of a “market” tends to be presented in math-heavy econ courses, and the parts I’d consider most central typically see surprisingly little coverage in more conceptual intro courses. So, this post aims to explain what I consider the central concepts of the mathematical notion of a market, without all the associated notation and jargon and proofs, in a way which lends itself to generalization beyond economics.
The Story About Apples And Bananas
We’ve got two people, Alice and Bob. Each of them can produce two goods, apples and bananas. Alice can use her land to produce five tons of apples, or one ton of bananas, or some proportional combination of the two. Bob can use his land to produce five tons of apples or twenty tons of bananas, or some proportional combination of the two. Both want a varied diet of apples and bananas.
… and you remember from econ 101 roughly how this goes, right? If the two just produce food for themselves separately, then each grows a mix of apples and bananas. But then Alice’ opportunity cost for one apple is 1/5 = 0.2 tons of bananas, whereas Bob’s opportunity cost for one apple is 20/5 = 4 tons bananas. So, the two could produce a pareto gain of apples and bananas by specializing: Alice can specialize more toward apple production, Bob can specialize more towards banana production. For instance, if Alice shifts production toward 1 more ton of apples, while Bob shifts production toward 1 less ton of apples, then together they produce - 0.2*1 + 4*1 = 3.8 tons more bananas with the same number of apples.
Now the key question for this post: when does this sort of specialization reach equilibrium? Under what conditions do Alice and Bob together decide that they’ve both specialized the correct amount, and don’t need to shift their production around any more?
In this exact example, they’ll only hit equilibrium once one of them is fully specialized - either Alice fully specialized in apples, or Bob fully specialized in bananas. Otherwise, they could always do better by specializing more. But in general, decreasing marginal returns might mean that both should be less-than-fully specialized - e.g. maybe both have some land better suited to apples and some better suited to bananas, so as they shift production their opportunity costs change.
So when will the two “reach equilibrium”? Well, when their opportunity costs are the same - i.e. when they have the same tradeoff between producing apples vs bananas.[1]
… and that’s a market.
More generally, we have:
Another Story: Stock Traders
We have a bunch of stock traders, each with a portfolio of stocks and cash, and a utility function over their portfolio which they seek to maximize. (We’ll assume, for simplicity, that the traders are not updating their beliefs over the course of this story, so we can ignore the “expectation” part of their expected utility maximization.)
Unlike the previous story, there’s no production, but each trader still has an implicit tradeoff rate between stocks - e.g. for each trader, there is some number of GOOG stocks which they’d be willing to trade for one TSLA. And if two traders have different tradeoff rates - e.g. they’re willing to trade off TSLA for GOOG in different ratios - then the two can make a mutually beneficial trade. The trader who’s willing to trade more GOOG for TSLA can “specialize more in GOOG” and the trader who’s willing to trade less GOOG for TSLA can “specialize more in TSLA”; they trade GOOG for TSLA and both end up with higher utility.[2]
So we have a similar equilibrium story to before: traders equilibrate when they’re all willing to trade off between different stocks and cash at the same ratios. And that defines a market: once the traders equilibrate, the ratios at which they’re collectively willing to trade are the “market prices”, and the traders themselves form the market.
Two side-notes on this example, both of which generalize.
First, to keep things simple here, I’m assuming/approximating that there’s zero bid-ask spread, i.e. if a trader’s marginal tradeoff rate between GOOG and TSLA is 2:3 then they’re willing to trade either 3 GOOG for 2 TSLA or 2 TSLA for 3 GOOG. With nonzero bid-ask spread we need to represent the “prices” as intervals or polytopes or convex sets rather than real numbers, which makes things more mathematically complicated, but the intuitive picture remains similar.
Second, once there’s more than two goods, we still only need to keep track of one price for each good, rather than a tradeoff rate between each pair. Why? Well, suppose one trader prices GOOG at $150 and TSLA at $225 (a 2:3 price ratio). Since there’s zero spread, they’re willing to go either direction on either of those two trades ($ <-> GOOG and $ <-> TSLA), so implicitly, they’re willing to trade 3 GOOG for 2 TSLA (via 3 GOOG <-> $450 <-> 2 TSLA) in either direction. So, by specifying the marginal tradeoff rates with respect to one reference good (e.g. $, in this example), we specify all the pairwise marginal tradeoff rates implicitly.
Temperature
Time for an example which illustrates the breadth of applicability.
Isolated physical systems have two central thermodynamic quantities: internal energy, and (neg-)entropy. The rate at which those two “trade off” is temperature: temperature quantifies how much entropy changes if a unit of internal energy is added to the system. (Indeed, temperature is often defined that way.)
If two systems are at different temperatures, then they have different tradeoff rates between energy and entropy. So, a unit of energy can be removed from one and added to the other, with a net increase in entropy. Systems equilibrate when the tradeoff rates - i.e. temperatures - are the same.
So, we can view a bunch of physical systems at thermal equilibrium as a market. The “goods” are energy and entropy, and these can be exchanged between subsystems in order to increase overall entropy. At equilibrium, the shared “market price” is the temperature of all the systems.
The Key Principle: Pareto Optimality with Multiple Subsystems
Two key ideas unify these examples. First, there are multiple “goals” - maybe multiple goods, maybe multiple agents’ utilities, maybe energy and entropy - and the system “equilibrates” at a pareto optimum of those goals. Second, there are multiple subsystems, each of which can contribute to the different goals.
Pareto optimality implies an (implicit) set of “prices” - i.e. marginal tradeoff rates between the goals. As with the stock traders example, once we know the marginal tradeoff rates between each goal and one (arbitrary) reference goal, that specifies the full set of “prices” - the pairwise tradeoff rates between goals.
So, assuming each subsystem can’t achieve a pareto improvement in the goals by itself, each subsystem has an implicit set of prices for the goals. But before equilibration, those prices could be different for the different subsystems, in which case a marginal pareto improvement can be achieved by jointly tweaking any two subsystems with different prices. Equilibrium is defined by the absence of any more pareto improvements, which implies that the subsystems all have the same implied prices.
And that’s the core concept of a market: a bunch of subsystems at pareto optimality with respect to a bunch of goals. The core mathematical reason why this kind of “market” is interesting and useful to think about is that, whenever a bunch of subsystems are at pareto optimality with respect to a bunch of goals, they must all have the same implied “prices” (i.e. marginal tradeoff rates) for those goals. Whenever two subsystems have different implied prices, a marginal pareto gain can be achieved by jointly optimizing the two, so the two are “out of equilibrium”.
Full specialization is included as a corner-case of “opportunity costs are the same”. Conceptually: when there’s a “corner” in the production curve, we can view the slope of the curve (i.e. the opportunity cost) as being anything between the cost on one side and the cost on the other side. In that case, the tradeoff rate has to be represented as an interval or polytope or convex set rather than a real number. Search jargon: subgradient calculus.
By this point someone often chimes in and says “but maybe that trade made third parties worse off!” and then someone else says “only relative to some weird choice of baseline which wasn’t a very natural baseline in the first place” and then they start arguing about free market policies and, like, I don’t give a shit. This post is not primarily about agents’ welfare, it is about equilibrium conditions.
Also I have a whole post titled Comparative Advantage is Not About Trade, if you want to see the sort of principles in this post applied in a more explicitly economic setting while still trying to emphasize that it's not really about interminable free market political debates.