I played around with the example as well and got similar results. I was wondering why there are two more dominant PCs: If you assume there is no bias, then the activations will all look like
or and I checked that the two directions found by the PC approximately span the same space as . I suspect something similar is happening with bias.
In this specific example there is a way to get the true direction w_out from the activations: By doing a PCA on the gradient of the activations. In this case, it is easily explained by computing the gradients by hand: It will be a multiple of w_out.
See the second to last paragraph. The gradients of downstream quantities with respect to the activations contains information and structure that is not part of the activations. So in principle, there could be a general way to analyse the right gradients in the right way on top of the activations to find the features of the model. See e.g. this for an attempt to combine PCAs of activations and gradients together.
Thanks for the reference, I wanted to illuminate the value of gradients of activations in this toy example as I have been thinking about similar ideas.
I personally would be pretty excited about attribuition dictionary learning, but it seems like nobody did that on bigger models yet.
In my limited experience, attribution-patching style attributions tend to be a pain to optimise for sparsity. Very brittle. I agree it seems like a good thing to keep poking at though.
The third term in that. Though it was in a somewhat different context related to the weight partitioning project mentioned in the last paragraph, not SAE training.
Yes, brittle in hyperparameters. It was also just very painful to train in general. I wouldn't straightforwardly extrapolate our experience to a standard SAE setup though, we had a lot of other things going on in that optimisation.
I found this clear and useful, thanks. Particularly the notes about compositional structure. For what it's worth I'll repeat here a comment from ILIAD, which is that there seems to be something in the direction of SAEs, approximate sufficient statistics/information bottleneck, the work of Achille-Soatto and SLT (Section 5 iirc) which I had looked into after talking with Olah and Wattenberg about feature geometry but which isn't currently a high priority for us. Somebody might want to pick that up.
Nice post! Re issue 1, there are a few things that you can do to work out if a representation you have found is a 'model feature' or a 'dataset feature'. You can:
Check if intervening on the forward pass to modify this feature produces the expected effect on outputs. Caveats:
- the best vector for probing is not the best vector for steering (in general the inverse of a matrix is not the transpose, and finding a basis of steering vectors from a basis of probe vectors involves inverting the basis matrix)
- It's possible that the feature you found is causally upstream of some features the model has learned, and even if the model hasn't learned this feature, changing it affects things the model is aware of. OTOH, I'm not sure whether I want to say that this feature has not been learned by the model in this case.
- Some techniques eg crosscoders don't come equipped with a well defined notion of intervening on the feature during a forward pass.
Nonetheless, we can still sometimes get evidence this way, in particular about whether our probe has found subtle structure in the data that is really causally irrelevant to the model. This is already a common technique in interpretability (see eg the initimitable golden gate claude, and many more systematic steering tests like this one),
- Run various shuffle/permutation controls:
- Measure the selectivity of your feature finding technique: replace the structure in the data with some new structure (or just remove the structure) and then see if your probe finds that new structure. To the extent that the probe can learn the new structure, it is not telling you about what the model has learned.
Most straightforwardly: if you have trained a supervised probe, you can train a second supervised probe on a dataset with randomised labels, and look at how much more accurate the probe is when trained on data with true labels. This can help distinguish between the hypothesis that you have found a real variable in the model, and the null hypothesis that the probing technique is powerful enough to find a direction that can classify any dataset with that accuracy. Selectivity tests should do things like match the bias of the train data (eg if training a probe on a sparsely activating feature, then the value of the feature is almost always zero and that should be preserved in the control).
You can also test unsupervised techniques like SAEs this way by training them on random sequences of tokens. There's probably more sophisticated controls that can be introduced here: eg you can try to destroy all the structure in the data and replace it with random structure that is still sparse in the same sense, and so on. - In addition to experiments that destroy the probe training data, you can also run experiments that destroy the structure in the model weights. To the extent that the probe works here, it is not telling you about what the model has learned.
For example, reinitialise the weights of the model, and train the probe/SAE/look at the PCA directions. This is a weak control: a stronger control could do something like reiniatialising the weights of the model that matches the eigenspectrum of each weight matrix to the eigenspectrum of the corresponding matrix in the trained model (to rule out things like the SAE didn't work in the randomised model because the activation vector is too small etc), although that control is still quite weak.
This control was used nicely in Towards Monosemanticity here, although I think much more research of this form could be done with SAEs and their cousins. - I am told by Adam Shai that in experimental neuroscience, it is something of a sport to come up with better and better controls for testing the hypothesis that you have identified structure. Maybe some of that energy should be imported to interp?
- Measure the selectivity of your feature finding technique: replace the structure in the data with some new structure (or just remove the structure) and then see if your probe finds that new structure. To the extent that the probe can learn the new structure, it is not telling you about what the model has learned.
- Probably some other things not on my mind right now??
I am aware that there is less use in being able to identify whether your features are model features or dataset features than there is in having a technique that zero-shot identifies model features only. However, a reliable set of tools for distinguishing what type of feature we have found would give us feedback loops that could help us search for good feature-finding techniques. eg. good controls would give us the freedom to do things like searching over (potentially nonlinear) probe architectures for those with a high accuracy relative to the control (in the absence of the control, searching over architectures would lead us to more and more expressive nonlinear probes that tell us nothing about the model's computation). I'm curious if this sort of thing would lead us away from treating activation vectors in isolation, as the post argues.
the best vector for probing is not the best vector for steering
I don't understand this. If a feature is represented by a direction v in the activations, surely the best probe for that feature will also be v because then <v,v> is maximized.
the best vector for probing is not the best vector for steering
AKA the predict/control discrepancy, from Section 3.3.1 of Wattenberg and Viegas, 2024
[edit: I'm now thinking that actually the optimal probe vector is also orthogonal to so maybe the point doesn't stand. In general, I think it is probably a mistake to talk about activation vectors as linear combinations of feature vectors, rather than as vectors that can be projected into a set of interpretable readoff directions. see here for more.]
Yes, I'm calling the representation vector the same as the probing vector. Suppose my activation vector can be written as where are feature values and are feature representation vectors. Then the probe vector which minimises MSE (explains most of the variance) is just . To avoid off target effects, the vector you want to steer with for feature might be the vector that is most 'surgical': it only changes the value of this feature and no other features are changed. In that case it should be the vector that lies orthogonal to which is only the same as if the set are orthogonal.
Obviously I'm working with a non-overcomplete basis of feature representation vectors here. If we're dealing with the overcomplete case, then it's messier. People normally talk about 'approximately orthogonal vectors' in which case the most surgical steering vector but (handwaving) you can also talk about something like 'approximately linearly independent vectors' in which case my point stands I think (note that SAE decoder directions are definitely not approximately orthogonal). For something less handwavey see this appendix.
A thought triggered by reading issue 3:
I agree issue 3 seems like a potential problem with methods that optimise for sparsity too much, but it doesn't seem that directly related to the main thesis? At least in the example you give, it should be possible in principle to notice that the space can be factored as a direct sum without having to look to future layers. I guess what I want to ask here is:
It seems like there is a spectrum of possible views you could have here:
- It's achievable to come up with sensible ansatzes (sparsity, linear representations, if we see the possibility to decompose the space into direct sums then we should do that, and so on) which will get us most of the way to finding the ground truth features, but there are edge cases/counterexamples which can only be resolved by looking at how the activation vector is used. this is compatible with the example you gave in issue 3 where the space is factorisable into a direct sum which seems pretty natural/easy to look for in advance, although of course that's the reason you picked that particular structure as an example.
- There are many many ways to decompose an activation vector, corresponding to many plausible but mutually incompatible sets of ansatzes, and the only way to know which is correct for the purposes of understanding the model is to see how the activation vector is used in the later layers.
- Maybe there are many possible decompositions but they are all/mostly straightforwardly related to each other by eg a sparse basis transformation, so finding any one decomposition is a step in the right direction.
- Maybe not that.
- Any sensible approach to decomposing an activation vector without looking forward to subsequent layers will be actively misleading. The right way to decompose the activation vector can't be found in isolation with any set of natural ansatzes because the decomposition depends intimately on the way the activation vector is used.
The main strategy being pursued in interpretability today is (insofar as interp is about fully understanding models):
- First decompose each activation vector individually. Then try to integrate the decompositions of different layers together into circuits. This may require merging found features into higher level features, or tweaking the features in some way, or filtering out some features which turn out to be dataset features. (See also superseding vs supplementing superposition).
This approach is betting that the decompositions you get when you take each vector in isolation are a (big) step in the right direction, even if they require modification, which is more compatible with stance (1) and (2a) in the list above. I don't think your post contains any knockdown arguments that this approach is doomed (do you agree?), but it is maybe suggestive. It would be cool to have some fully reverse engineered toy models where we can study one layer at a time and see what is going on.
I agree issue 3 seems like a potential problem with methods that optimise for sparsity too much, but it doesn't seem that directly related to the main thesis? At least in the example you give, it should be possible in principle to notice that the space can be factored as a direct sum without having to look to future layers.
Sure, it's possible in principle to notice that there is a subspace that can be represented factored into a direct sum. But how do you tell whether you in fact ought to represent it in that way, rather than as composed features, to match the features of the model? Just because the compositional structure is present in the activations doesn't mean the model cares about it.
I don't think your post contains any knockdown arguments that this approach is doomed (do you agree?), but it is maybe suggestive.
I agree that it is not a knockdown argument. That is why the title isn't "Activation space interpretability is doomed."
Nice post! I think these are good criticisms that don't justify the title. Points 1 through 4 are all (specific, plausible) examples of ways we may interpret the activation space incorrectly. This is worth keeping in mind, and I agree that just looking at the activation space of a single layer isn't enough, but it still seems like a very good place to start.
A layer's activation is a relatively simple space, constructed by the model, that contains all the information that the model needs to make its prediction. This makes it a great place to look if you're trying to understand how the model's thinking.
Really liked this post!
Just for my understanding:
You mention trans/cross-coders as possible solutions to the listed problems, but they also fall prey to issues 1 & 3, right?
Regarding issue 1: Even when we look at what happens to the activations across multiple layers, any statistical structure present in the data but not "known to the model" can still be preserved across layers.
For example: Consider a complicated curve in 2D space. If we have an MLP that simply rotates this 2D space, without any knowledge that the data falls on a curve, a Crosscoder trained on the pre-MLP & post-MLP residual stream would still decompose the curve into distinct features. Similarly, a Transcoder trained to predict the post-MLP from the pre-MLP residual stream would also use these distinct features and predict the rotated features from the non-rotated features.
Regarding issue 3: I also don't see how trans/cross-coders help here. If we have multiple layers where the {blue, red} ⊗ {square, circle} decomposition would be possible, I don't see why they would be more likely than classic SAEs to find this product structure rather than the composed representation.
Yes, that's right -- see footnote 10. We think that Transcoders and Crosscoders are directionally correct, in the sense that they leverage more of the models functional structure via activations from several sites, but agree that their vanilla versions suffer similar problems to regular SAEs.
This is also a concern I have but I feel like steering / project out is kinda sufficient to understand if the model uses this feature.
How do you know what "ideal behaviour" is after you steer or project out your feature? How would you differentiate a feature with sufficiently high cosine sim to a "true model feature" and a "true model feature"? I agree you can get some signal on whether a feature is causal, but would argue this is not ambitious enough.
Excellent work and I think you raise a lot of really good points, which help clarify for me why this research agenda is running into issues, and I think ties in to my concerns about activation space work engendered by recent success in latent obfuscation (https://arxiv.org/abs/2412.09565v1).
In a way that does not affect the larger point, I think that your framing of the problem of extracting composed features may be slightly too strong: in a subset of cases, e.g. if there is a hierarchical relationship between features (https://www.lesswrong.com/posts/XHpta8X85TzugNNn2/broken-latents-studying-saes-and-feature-co-occurrence-in) SAEs might be able to pull out groups of latents that act compositionally (https://www.lesswrong.com/posts/WNoqEivcCSg8gJe5h/compositionality-and-ambiguity-latent-co-occurrence-and). The relationship to any underlying model compositional encoding is unclear, this probably only works in a few cases, and generally does not seem like a scalable approach, but I think that SAEs may be doing something more complex/weirder than only finding composed features.
Thank you. Yes, our claim isn't that SAEs only find composed features. Simple counterexample: Make a product space of two spaces with dictionary elements each, with an average of features active at a time in each factor space. Then the dictionary of composed features has an of , whereas the dictionary of factored features has an of , so a well-tuned SAE will learn the factored set of features. Note however that just because the dictionary of factored features is sparser doesn't mean that those are the features of the model. The model could be using the composed features instead, because that's more convenient for the downstream computations somehow, or for some other reason.
Our claim is that an SAE trained on the activations at a single layer cannot tell whether the features of the model are in composed representation or factored representation, because the representation the model uses need not be the representation with the lowest .
I agree with much of this, but I suspect people aren't only sticking with activation-based interpretability because the bad dimensionality of weight-based interpretability is intimidating. Rather, I feel like we have to be thinking about activation-based interpretability if we want an analysis of the model's behavior to contain semantics that are safety-relevant.
For example, I can know nothing about how safe a classifier that distinguishes A from B is, regardless of how much I know about its weights, unless I know what A and B are. There might be identical sets of weights that are safe if acting on one problem distribution but unsafe if acting on another. We've got to characterize the problem distribution to assess safety.
By the good regulator theorem, it is true that if a model works well, it will carry some kind of weak copy of the training dataset inside its weights. In this sense, it might be reasonable to think that models might "inherit" semantic features of the datasets they're operating on, and maybe this provides some way to bridge between weight based interpretability and human values regarding the outputs of model. However, lots and lots of information can be lost in the process because a good regulator only cares about reflecting the data insofar as doing so improves its performance on the task it's conducting. Anything that isn't a sufficient statistic for doing that task given the particular dataset it has on hand can be lost.
I really feel like omitted variables make any form of interpretability, weight based or not, a doomed strategy for safety, at least interpretability in a vacuum without supplementation from other strategies. How are we supposed to detect the absence of a concept or value that the model ought to possess just from its weights or activations? Interpretability can only tell us what a model's doing, but nothing about what it's not. Analyzing the safety of the outputs doesn't scale well for models that are smarter than us, but I think it's a necessary requirement regardless.
(We might try to characterize omitted variables as undesirable invariances in the model's behavior, changes to the inputs that should change its activations in certain ways but don't. However, exhaustively describing all the undesired invariances or knowing which changes to make to the inputs or the corresponding activations we want to see associated with them all seems prohibitive, and this risks running into problems with the principle of indifference, so I don't think it can work.)
We've done some studies of related phenomena in: https://openreview.net/forum?id=aY2nsgE97a — e.g., that the activation patterns can be strongly biased towards capturing easy (linear) features over difficult (nonlinear) ones (or more prevalent over less prevalent ones, or earlier-learned ones, etc.), which can lead interpretations based on activations to miss some of the important features that the model is computing.
I agree that the ultimate goal is to understand the weights. Seems pretty unclear whether trying to understand the activations is a useful stepping stone towards that. And it's hard to be sure how relevant theoretical toy example are to that question.
This was a really thought-provoking post; thanks for writing it! I thought this was an unusually good attempt to articulate problems with the current interpretability paradigm and do some high-level thinking about what we could do differently. However, I think a few of the specific points are weaker than you make them seem in a way that somewhat contradicts the title of the post. I also may be misunderstanding parts, so please let me know if that’s the case.
Problems 2 and 3 (the learned feature dictionary may not match the model’s feature dictionary, and activation space interpretability can fail to find compositional structure) both seem to be specific instances of ‘you are finding the right underlying features, but broken down differently from how the model is actually thinking about them’. This seems like a double edged sword to me. On one hand, it would be nice to know what level of abstraction the model is using. On the other hand, it’s useful to be able to analyze the computation at different levels of abstraction. And, if the model is breaking things down differently from the exact features you find, you may be able to piece this together from its downstream computation. I think these problems could just as easily be seen as a good thing, and they definitely don’t doom activation-space interpretability.
Problem 1, activations can contain structure of the data distribution that the models themselves don’t ‘know’ about, seems correct. However, this largely seems solvable by taking into account the effect of features on the output. Eg, as you later mention, attribution dictionary learning and E2E SAEs both seem like great attempts to tackle this problem.
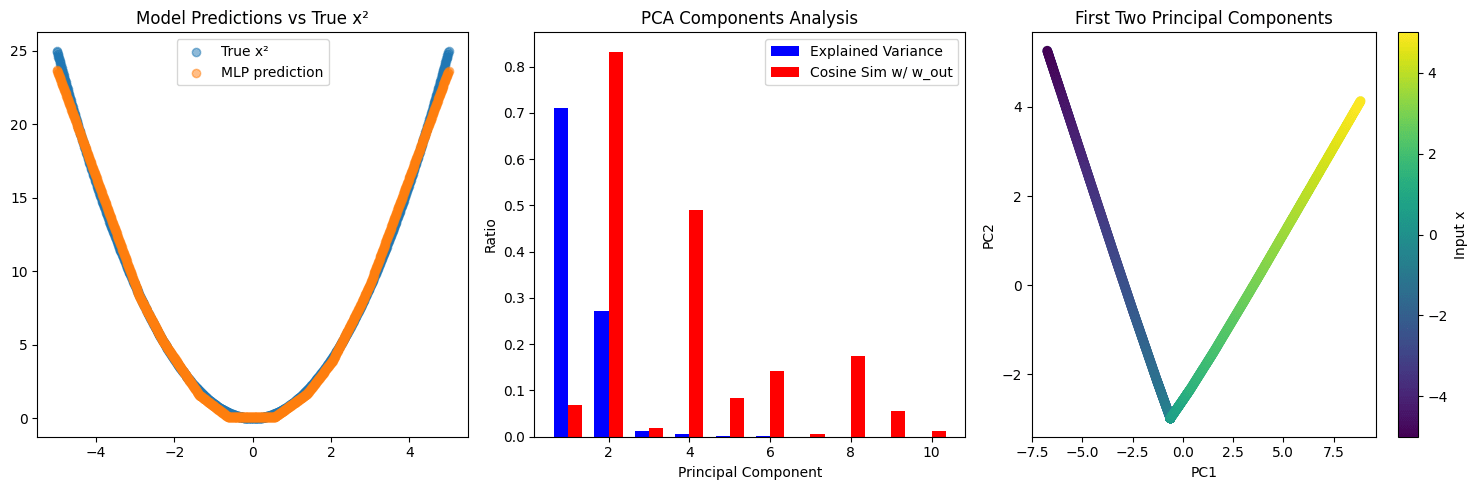
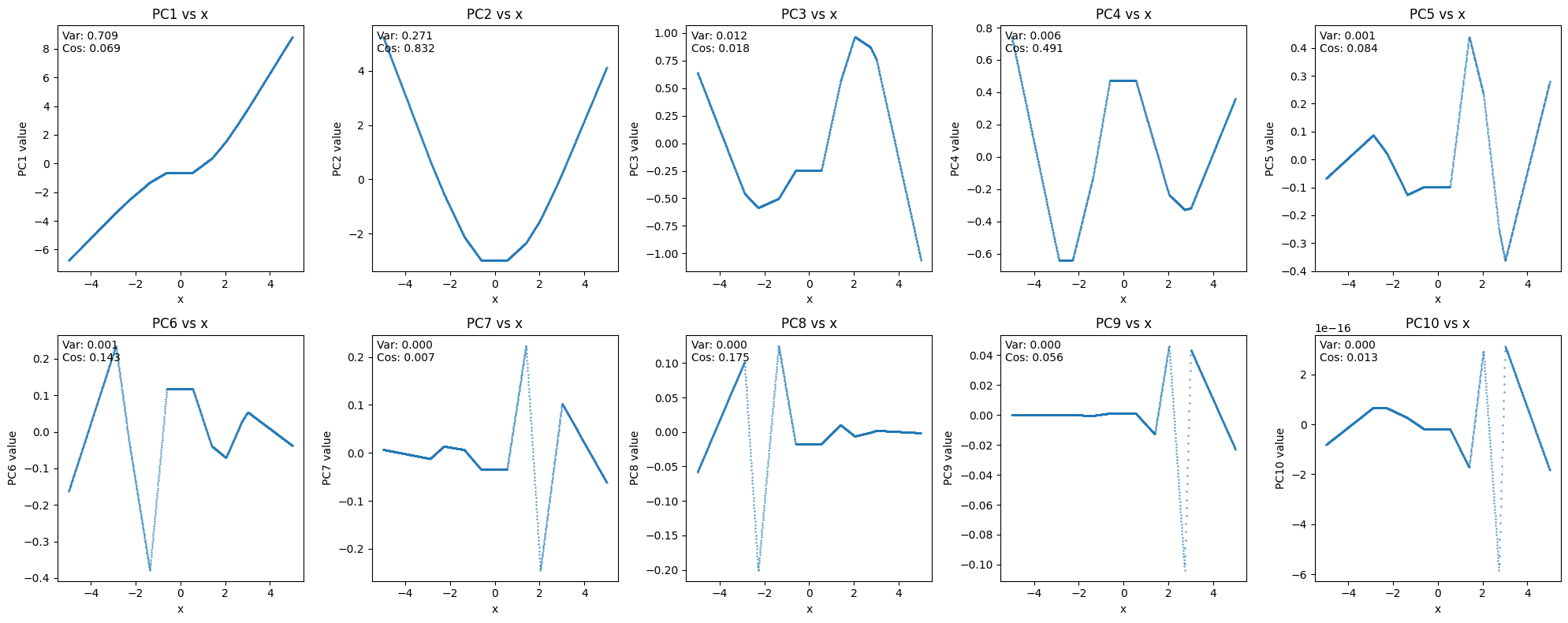
Re problem 4, function approximation creates artefacts: in general, it’s never possible to distinguish orthogonal directions without figuring out what class of input examples the feature fires on. For instance, in the example, you might end up with 5-10 different features activating to reconstruct something as simple as a representation of . But these features would faithfully activate on inputs where the model needs to compute , at least as well as any other normal feature activates on related inputs. Additionally, insofar as these 5-10 features are confusing, you can still find the x^2 feature in the network’s downstream computation, e.g. by using transcoders.
One problem here is that your SAEs could get overwhelmed with too many function approximation features, making it much more difficult to analyze. I don’t have strong priors on whether or not this is true, but from the empirical results, I tentatively don’t think it is?
Again, thanks for writing the post, and please let me know if I’m missing anything / if you have general thoughts on this comment (:
My general issue with most of your counterpoints is that they apply just as much to the standard basis of the network. That is, the neurons in the MLPs, the residual stream activations as they are in Pytorch, etc. .
The standard basis represents the activations of the network completely faithfully. It does this even better than techniques like SAEs, which always have some amount of reconstruction error. All the model's features will be linear combinations of activations in the standard basis, so it does have 'the right underlying features, but broken down differently from how the model is actually thinking about them'.
Same for all your other points. Theoretically, can you solve problems 1, 2 and 3 with the standard basis by taking information about how the model is computing downstream into account in the right way? Sure. You'd 'take it into account' by finding some completely new basis. Can you solve problem 4 with transcoders? I think vanilla versions would struggle, because the transcoder needs to combine many latents to form an , but probably.
But our point is that 'piecing together the model's features from its downstram computations' is the whole job of a decomposition. If you have to use information about the model's computations to find the features of the model, you're pretty much conceding that what we call activation space interpretability here doesn't work:
What do we mean by activation space interpretability? Interpretability work that attempts to understand neural networks by explaining the inputs and outputs of their layers in isolation. In this post, we focus in particular on the problem of decomposing activations, via techniques such as sparse autoencoders (SAEs), PCA, or just by looking at individual neurons. This is in contrast to interpretability work that leverages the wider functional structure of the model and incorporates more information about how the model performs computation. Examples of existing techniques using such information include Transcoders, end2end-SAEs and joint activation/gradient PCAs.
I am also skeptical that the techniques you name (e2e SAEs, transcoders, sparse dictionary learning on attributions) suffice to solve all problems in this class in their current form. That would have been a separate discussion beyond the scope of this post though. All we're trying to say here is that you do very likely need to leverage the wider functional structure of the model and incorporate more information about how the model performs computation to decompose the model well.
Thanks for the response! I still think that most of the value of SAEs comes from finding a human-interpretable basis, and most of these problems don't directly interfere with this property. I'm also somewhat skeptical that SAEs actually do find a human-interpretable basis, but that's a separate question.
All the model's features will be linear combinations of activations in the standard basis, so it does have 'the right underlying features, but broken down differently from how the model is actually thinking about them'.
I think this is a fair point. I also think there's a real sense in which it's useful to know that the model is representing the concepts "red" and "square," even if it's thinking of them in terms of the Red feature and the Square feature and your SAE found the "red square" feature. It's much harder to figure out what concepts the model is representing in human interpretable terms by staring at activations in a standard basis. There's a big difference between "we know what human-interpretable concepts the model is representing but not exactly what structure it uses to think of them" and "we just don't know what concepts the model is representing to begin with." I think if we could do the former well, that would already be amazing.
Put slightly more strongly:
The question of whether the model thinks in terms of "red square" or "red and "square" is moot, because the model does not actually think in terms of these concepts to begin with. The model thinks in its own language, and our job is to translate that language to our own. In this {red, blue} X {square, circle} space, looking at the attribution of "red square" and "red circle" to downstream features should give us the same result as looking at the attribution of "red" to downstream features, since red square and red circle encompass the full range of possibilities of things that can be red. It might be more convenient for us if we find the features that make the models attribution graph as simple as possible across a wide range of input examples, but there's no real sense in which we're misrepresenting its thought process.
Same for all your other points. Theoretically, can you solve problems 1, 2 and 3 with the standard basis by taking information about how the model is computing downstream into account in the right way? Sure. You'd 'take it into account' by finding some completely new basis.
Solving problem 1 could just entail adjusting the SAE basis while retaining most of its value! Solving problems 2 and 3 would require finding a basis which represents the same human-interpretable features but in a somewhat different way. Insofar as SAE features are actually human-interpretable (which I'm often skeptical of), I think this basis adds a ton of value.
I am also often skeptical of SAEs, but I feel that the biggest problem is that they don't actually capture the sum of the concepts the model is representing in a human-interpretable way. If they actually did this correctly, I would happily forgo knowing the exact structure the model uses to think of them, and I would be alright if there were extra artifacts that made them harder to analyze.
(Also, oops, I didn't realize that by activation-space you meant one layer's activations only).
TL;DR: There may be a fundamental problem with interpretability work that attempts to understand neural networks by decomposing their individual activation spaces in isolation: It seems likely to find features of the activations - features that help explain the statistical structure of activation spaces, rather than features of the model - the features the model’s own computations make use of.
Written at Apollo Research
Introduction
Claim: Activation space interpretability is likely to give us features of the activations, not features of the model, and this is a problem.
Let’s walk through this claim.
What do we mean by activation space interpretability? Interpretability work that attempts to understand neural networks by explaining the inputs and outputs of their layers in isolation. In this post, we focus in particular on the problem of decomposing activations, via techniques such as sparse autoencoders (SAEs), PCA, or just by looking at individual neurons. This is in contrast to interpretability work that leverages the wider functional structure of the model and incorporates more information about how the model performs computation. Examples of existing techniques using such information include Transcoders, end2end-SAEs and joint activation/gradient PCAs.
What do we mean by “features of the activations”? Sets of features that help explain or make manifest the statistical structure of the model’s activations at particular layers. One way to try to operationalise this is to ask for decompositions of model activations at each layer that try to minimise the description length of the activations in bits.
What do we mean by “features of the model”? The set of features the model itself actually thinks in, the decomposition of activations along which its own computations are structured, features that are significant to what the model is doing and how it is doing it. One way to try to operationalise this is to ask for the decomposition of model activations that makes the causal graph of the whole model as manifestly simple as possible: We make each feature a graph node, and draw edges indicating how upstream nodes are involved in computing downstream nodes. To understand the model, we want the decomposition that results in the most structured graph with the fewest edges, with meaningfully separate modules corresponding to circuits that do different things.
Our claim is pretty abstract and general, so we’ll try to convey the intuition behind it with concrete and specific examples.
Examples illustrating the general problem
In the following, we will often use SAEs as a stand-in for any technique that decomposes individual activation spaces into sets of features. But we think the problems these examples are trying to point to apply in some form to basically any technique that tries to decompose individual activation spaces in isolation.[1]
1. Activations can contain structure of the data distribution that the models themselves don’t ‘know’ about.
Consider a simple model that takes in a two-dimensional input (x,y) and computes some scalar function of the two, f(x,y). Suppose for all data points in the data distribution, the input data (x,y) falls on a very complicated one-dimensional curve. Also, suppose that the trained model is blind to this fact and treats the two input variables as entirely independent (i.e. none of the model’s computations make use of the relationship between x and y). If we were to study the activations of this model, we might notice this curve (or transformed curve) and think it meaningful.
In general, data distributions used for training (and often also interpreting) neural networks contain a very large amount of information about the process that created said dataset. For all non-toy data distributions, the distribution will reflect complex statistical relationships of the universe. A model with finite capacity can't possibly learn to make use of all of these relationships. Since activations are just mathematical transformations of inputs sampled from this data distribution, by studying neural networks through their distribution of activations, we should expect to see many of those unused relationships in the activations. So, fully understanding the model’s activations can in a sense be substantially harder than fully understanding what the model is doing. And if we don’t look at the computations the model is carrying out on those activations before we try to decompose them, we might struggle to tease apart properties of the input distribution and properties of the model.[2]
2. The learned feature dictionary may not match the “model’s feature dictionary”.
Now let’s consider another one-dimensional curve, this time embedded in a ten-dimensional space.[3] One of the nice things about sparse dictionary methods like SAEs is that they can approximate curves like this pretty well, using a large dictionary of features with sparse activation coefficients. If we train an SAE with a dictionary of size 500 on this manifold, we might find 500 features, only a very small number of which are active at a time, corresponding to different tiny segments of the curve.[4]
Suppose, however, that the model actually thinks of this single dense data-feature as a sparse set of 100 linear directions. We term this set of directions the “model’s dictionary”. The model’s dictionary approximates most segments of the curve with lower resolution than our dictionary, but it might approximate some crucial segments a lot more finely. MLPs and attention heads downstream in the model carry out computations on these 100 sparsely activating directions. The model’s decomposition of the ten-dimensional space into 100 sparse features and our decomposition of the space into 500 sparse features are necessarily quite different. Some features and activation coefficients in the two dictionaries might be closely related, but we should not expect most to be. If we are not looking at what the model does with these activations downstream, how can we tell that the feature dictionary we find matches the model’s feature dictionary? When we perform the decomposition, we don’t know yet what parts of the curve are more important for what the model is computing downstream, and thus how the model is going to think about and decompose the ten-dimensional subspace. We probably won’t even be aware in the first place that the activations we are decomposing lie on a one-dimensional curve without significant extra work.[5]
3. Activation space interpretability can fail to find compositional structure.
Suppose our model represents four types of object in some activation space: {blue square, red square, blue circle, red circle}.[6] We can think of this as the direct product space {blue, red} ⊗ {square, circle}. Suppose the model’s 'true features' are colour and shape, in the sense that later layers of the model read the 'colour' variable and the 'shape' variable independently. Now, suppose we train an SAE with 4 dictionary elements on this space. SAEs are optimised to achieve high sparsity -- few latents should be active on each forward pass. An SAE trained on this space will therefore learn the four latents {blue square, red square, blue circle, red circle} (the "composed representation"), rather than {blue, red} ⊗ {square, circle} (the "product representation"), as the former has sparsity 1, while the latter has sparsity 2. In other words, the SAE learns features that are compositions of the model’s features.
Can we fix this by adjusting the sparsity penalty? Probably not. Any sparse-dictionary approach set to decompose the space as a whole will likely learn this same set of four latents, as this latent set is sparser, with shorter description length than the product set.
While we could create some ansatz for our dictionary learning approach that specifically privileges the product configuration, this is cheating. How would we know the product configuration and not the composed configuration matches the structure of the model’s downstream computations in this case in advance, if we only look at the activations in isolation? And even if we do somehow know the product configuration is right, how would we know in advance to look for this specific 2x2 structure? In reality, it would additionally be embedded in a larger activation space with an unknown number of further latents flying around besides just shape and colour.
4: Function approximation creates artefacts that activation space interpretability may fail to distinguish from features of the model.
This one is a little more technical, so we’ll take it in two stages. First, a very simplified version, then something that’s closer to the real deal.
Example 4a: Approximating x2. Suppose we have an MLP layer that takes a scalar input x and is trained to approximate the scalar output x2. The MLP comprises a Win matrix (vector, really) of shape (1,10) that maps x to some pre-activation. This gets mapped through a ReLU, giving a 10 dimensional activation vector a. Finally, these are mapped to a scalar output via some Wout matrix of shape (10,1). Thus, concretely, this model is tasked with approximating x2 via a linear combination of ten functions of the form ReLU(ax+b). Importantly, the network only cares about one direction in the 10 dimensional activation space, the one which gives a good approximation of x2 and is projected off by Wout. There are 9 other orthogonal directions in the hidden space. Unless we know in advance that the network is trying to compute x2, this important direction will not stick out to us. If we train an SAE on the hidden activations, or do a PCA, or perform any other activation decomposition of our choice, we will get out a bunch of directions, and likely none of them will be x2.[7] What makes the x2 direction special is that the model uses it downstream (which, here, means that this direction is special in Wout). But that information can't be found in the hidden activations alone. We need more information.
Example 4b: Circuits in superposition. The obvious objection to Example 4a is that Wout is natively a rank one matrix, so the fact that only one direction in the 10 dimensional activation space matters is trivial and obvious to the researcher. So while we do need to use some information that isn’t in the activations, it’s a pretty straightforward thing to find. But if we extend the above example to something more realistic, it’s not so easy anymore. Suppose the model is computing a bunch of the above multi-dimensional circuits in superposition. For example, take an MLP layer instead with 40,000 neurons, computing 80,000 functions of (sparse) scalar inputs, each of which requires 10 neurons to compute, and writes the results to a 10,000 dimensional residual stream.[8][9] Each of these 80,000 circuits would then occupy some ten-dimensional subspace in the 40,000 dimensional activation space of the MLP, meaning the subspaces must overlap. Each of these subspaces may only have one direction that actually matters for downstream computation.
Our SAE/PCA/activation-decomposition-of-choice trained on the activation space will not be able to tell which directions are actually used by the model, and which are an artefact of computing the directions that do matter. They will decompose these ten-dimensional subspaces into a bunch of directions, which almost surely won’t line up with the important ones. To make matters worse, we might not immediately know that something went wrong with our decomposition. All of these directions might look like they relate to some particular subtask when studied through the lens of e.g. max activating dataset examples, since they’ll cluster along the circuit subspaces to some extent. So the decomposition could actually look very interesting and interpretable, with a lot of directions that appear to somewhat-but-not-quite make sense when we study them. However, these many directions will seem to interact with the next layer in a very complicated manner.
The general problem
Not all the structure of the activation spaces matters for the model’s computations, and not all the structure of the model’s computations is manifest in the structure of individual activation spaces.
So, if we are trying to understand the model by first decomposing its activation spaces into features and then looking at how these features interact and form circuits, we might get a complete mess of interactions that do not make the structure of the model and what it is doing manifest at all. We need to have at least some relevant information about how the model itself uses the activations before we pick our features, and include that information in the activation space decomposition. Even if our goal is just to understand an aspect of the model’s representation enough for a use case like monitoring, looking at the structure of the activation spaces rather than the structure of the model’s computations can give us features that don’t have a clean causal relationship to the model’s structure and which thus might mislead us.
What can we do about this?
If the problem is that our decomposition methodologies lack relevant information about the network, then maybe the solution is giving them more of it. How could we try to do this?
Guess the correct ansatz. We can try to make a better ansatz for our decompositions by guessing in advance how model computations are structured. This requires progress on interpretability fundamentals, through e.g. understanding the structure and purpose of feature geometry better. Note however that the current favoured roadmap for making progress on those topics seems to be “decompose the activations well, understand the resulting circuits and structure, and then hope this yields increased understanding”. This may be a bit of a chicken-and-egg situation.
Use activations (or gradients) from more layers. We can try to use information from more layers to look for decompositions that simplify the model as a whole. For example, we can decompose multiple layers simultaneously and impose a sparsity penalty on connections between features in different layers. Other approaches that fall vaguely in this category include end-to-end-SAEs, Attribution Dictionary Learning, Transcoders, and Crosscoders.[10]
Use weights instead of or to supplement activations. Most interpretability work studies activations and not weights. There are good reasons for this: activations are lower dimensional than weights. The curse of dimensionality is real. However, weights, in a sense, contain the entire functional structure of the model, because they are the model. It seems in principle possible to decompose weights into circuits directly, by minimising some complexity measure over some kind of weight partitioning, without any intermediary step of decomposing activations into features at all. This would be a reversal of the standard, activations-first approach, which aims to understand features first and later understand the circuits. Apollo Research are currently trying this.
Thanks to Andy Arditi, Dan Braun, Stefan Heimersheim and Lee Sharkey for feedback.
Unless we cheat by having extra knowledge about the model’s true features that lets us choose the correct form of the decomposition before we even start.
An additional related concern is that we might end up with different conclusions about our model if we study it through a different data-distribution-lens. This seems problematic if our end goal is to study the model, which surely has some ground truth set of features it uses, independently of the data-lens used to extract them. Empirically, we do find that the set of SAE features we discover are highly (SAE training) dataset dependent.
Data on this manifold is importantly not actually representable as a set of sparsely activating discrete features.
If we train SAEs on `blocks.0.hook_resid_pre` of gpt2-small, we find such a set, corresponding to the positional encoding.
Though note this particular citation is easy-mode due to the curve being low dimensional and easy to guess. We should not expect it to be this easy in general to find the structure of interest.
This example is inspired by this Anthropic blog post.
This seems like an easy experiment to do!
Note that this doesn’t have to be a continuous function like x2, a boolean circuit e.g. evaluating some logical statement as True/False works as well. The fundamental problem here is that many operations can’t and won’t be computed using only a single neuron per layer, but rather a specific linear combination of multiple neurons. So implementing them almost inevitably produces extra structure in the activations that won’t be used. This is not a problem with algorithmic tasks specifically.
See circuits in superposition for an explanation of how to compute more functions in a layer than we have neurons.
Of course, just doing something with activations or gradients is not enough; you have to do something that successfully deals with the kinds of counterexamples we list above. We doubt the vanilla version of any currently public technique does this for all relevant counterexamples or even all counterexamples we list here.