An Advent of Thought

[-]TsviBT6mo73

(I think this article represents substantive important original thinking, and should be studied by those interested in solving problems about deeply relating to alien minds (e.g. "solving alignment", in most of the relevant meanings of that). I didn't have time to read more than 1/3rd of it, but already learned from and was stimulated by what I did read.)

[-]Steven Byrnes6mo*Ω560

I kinda disagree with this post in general, I’m gonna try to pin it down but sorry if I mischaracterize anything.

So, there’s an infinite (or might-as-well-be-infinite) amount of object-level things (e.g. math concepts) to learn—OK sure. Then there’s an infinite amount of effective thinking strategies—e.g. if I see thus-and-such kind of object-level pattern, I should consider thus-and-such cognitive strategy—I’m OK with that too. And we can even build a hierarchy of those things—if I’m about to apply thus-and-such Level 1 cognitive strategy in thus-and-such object-level context, then I should first apply thus-and-such Level 2 cognitive strategy, etc. And all of those hierarchical levels can have arbitrarily much complexity and content. OK, sure.

But there’s something else, which is a very finite legible learning algorithm that can automatically find all those things—the object-level stuff and the thinking strategies at all levels. The genome builds such an algorithm into the human brain. And it seems to work! I don’t think there’s any math that is forever beyond humans, or if it is, it would be for humdrum reasons like “not enough neurons to hold that much complexity in your head at once”.

And then I’m guessing your response would be something like: there isn’t just one optimal “legible learning algorithm” as distinct from the stuff that it’s supposed to be learning. And if so, sure … but I think of that as kinda not very important. Here’s something related that I wrote here:

Here's an example: If you've seen a pattern "A then B then C" recur 10 times in a row, you will start unconsciously expecting AB to be followed by C. But "should" you expect AB to be followed by C after seeing ABC only 2 times? Or what if you've seen the pattern ABC recur 72 times in a row, but then saw AB(not C) twice? What "should" a learning algorithm expect in those cases?
You can imagine a continuous family of learning algorithms, that operate on the same underlying principles, but have different "settings" for deciding the answer to these types of questions.
And I emphasize that this is one of many examples. "How long should the algorithm hold onto memories (other things equal)?" "How similar do two situations need to be before you reason about one by analogizing to the other?" "How much learning model capacity is allocated to each incoming signal line from the retina?" Etc. etc.
In all these cases, there is no "right" answer to the hyperparameter settings. It depends on the domain—how regular vs random are the environmental patterns you're learning? How stable are they over time? How serious are the consequences of false positives vs false negatives in different situations?
There may be an "optimal" set of hyperparameters from the perspective of "highest inclusive genetic fitness in such-and-such specific biological niche". But there is a very wide range of hyperparameters which "work", in the sense that the algorithm does in fact learn things. Different hyperparameter settings would navigate the tradeoffs discussed above—one setting is better at remembering details, another is better at generalizing, another avoids overconfidence in novel situations, another minimizes energy consumption, etc. etc.

Anyway, I think there’s a space of legible learning algorithms (including hyperparameters) that would basically “work” in the sense of creating superintelligence, and I think there’s a legible explanation of why they work. But within this range, I acknowledge that it’s true that some of them will be able to learn different object-level areas of math a bit faster or slower, in a complicated way, for example. I just don’t think I care. I think this is very related to the idea in Bayesian rationality that priors don’t really matter once you make enough observations. I think superintelligence is something that will be do autonomous learning and figuring-things-out in a way that existing AIs can’t. Granted, there is no simple theory that predicts the exact speed that it will figure out any given object-level thing, and no simple theory that says which hyperparameters are truly optimal, but we don’t need such a theory, who cares, it can still figure things out with superhuman speed and competence across the board.

By the same token, nobody ever found the truly optimal hyperparameters for AlphaZero, if those even exist, but AlphaZero was still radically superhuman. If truly-optimal-AlphaZero would have only needed to self-play for 20 million games instead of 40 million to get to the same level, who cares, that would have only saved 12 hours of training or something.

[-]Kaarel6mo*100

Thank you for the comment!

First, I'd like to clear up a few things:

I do think that making an "approximate synthetic 2025 human newborn/fetus (mind)" that can be run on a server having 100x usual human thinking speed is almost certainly a finite problem, and one might get there by figuring out what structures are there in a fetus/newborn precisely enough, and it plausibly makes sense to focus particularly on structures which are more relevant to learning. If one were to pull this off, one might then further be able to have these synthetic fetuses grow up quickly into fairly normal humans and have them do stuff which ends the present period of (imo) acute x-risk. (And the development of thought continues after that, I think; I'll say more that relates to this later.) While I do say in my post that making mind uploads is a finite problem, it might have been good to state also (or more precisely) that this type of thing is finite.
I certainly think that one can make a finite system such that one can reasonably think that it will start a process that does very much — like, eats the Sun, etc.. Indeed, I think it's likely that by default humanity would unfortunately start a process that gets the Sun eaten this century. I think it is plausible there will be some people who will be reasonable in predicting pretty strongly that that particular process will get the Sun eaten. I think various claims about humans understanding some stuff about that process are less clear, though there is surely some hypothetical entity that could pretty deeply understand the development of that process up to the point where it eats the Sun.
Some things in my notes were written mostly with an [agent foundations]y interlocutor in mind, and I'm realizing now that some of these things could also be read as if I had some different interlocutor in mind, and that some points probably seem more incongruous if read this way.

I'll now proceed to potential disagreements.

But there’s something else, which is a very finite legible learning algorithm that can automatically find all those things—the object-level stuff and the thinking strategies at all levels. The genome builds such an algorithm into the human brain. And it seems to work! I don’t think there’s any math that is forever beyond humans, or if it is, it would be for humdrum reasons like “not enough neurons to hold that much complexity in your head at once”.

Some ways I disagree or think this is/involves a bad framing:

If we focus on math and try to ask some concrete question, instead of asking stuff like "can the system eventually prove anything?", I think it is much more appropriate to ask stuff like "how quickly can the system prove stuff?". Like, brute-force searching all strings for being a proof of a particular statement can eventually prove any provable statement, but we obviously wouldn't want to say that this brute-force searcher is "generally intelligent". Very relatedly, I think that "is there any math which is technically beyond a human?" is not a good question to be asking here.
The blind idiot god that pretty much cannot even invent wheels (ie evolution) obviously did not put anything approaching the Ultimate Formula for getting far in math (or for doing anything complicated, really) inside humans (even after conditioning on specification complexity and computational resources or whatever), and especially not in an "unfolded form"^[1], right? Any rich endeavor is done by present humans in a profoundly stupid way, right?^[2] Humanity sorta manages to do math, but this seems like a very weak reason to think that [humans have]/[humanity has] anything remotely approaching an "ultimate learning algorithm" for doing math?^[3]
The structures in a newborn [that make it so that in the right context the newborn grows into a person who (say) pushes the frontier of human understanding forward] and [which participate in them pushing the frontier of human understanding forward] are probably already really complicated, right? Like, there's already a great variety of "ideas" involved in the "learning-relevant structures" of a fetus?
I think that the framing that there is a given fixed "learning algorithm" in a newborn, such that if one knew it, one would be most of the way there to understanding human learning, is unfortunate. (Well, this comes with the caveat that it depends on what one wants from this "understanding of human learning" — e.g., it is probably fine to think this if one only wants to use this understanding to make a synthetic newborn.) In brief, I'd say "gaining thinking-components is a rich thing, much like gaining technologies more generally; our ability to gain thinking-components is developing, just like our ability to gain technologies", and then I'd point one to Note 3 and Note 4 for more on this.
I want to say more in response to this view/framing that some sort of "human learning algorithm" is already there in a newborn, even in the context of just the learning that a single individual human is doing. Like, a human is also importantly gaining components/methods/ideas for learning, right? For example, language is centrally involved in human learning, and language isn't there in a fetus (though there are things in a newborn which create a capacity for gaining language, yes). I feel like you might want to say "who cares — there is a preserved learning algorithm in the brain of a fetus/newborn anyway". And while I agree that there are very important things in the brain which are centrally involved in learning and which are fairly unchanged during development, I don't understand what [the special significance of these over various things gained later] is which makes it reasonable to say that a human has a given fixed "learning algorithm". An analogy: Someone could try to explain structure-gaining by telling me "take a random init of a universe with such and such laws (and look along a random branch of the wavefunction^[4]) — in there, you will probably eventually see a lot of structures being created" — let's assume that this is set up such that one in fact probably gets atoms and galaxies and solar systems and life and primitive entities doing math and reflecting (imo etc.). But this is obviously a highly unsatisfying "explanation" of structure-gaining! I wanted to know why/how protons and atoms and molecules form and why/how galaxies and stars and black holes form, etc.. I wanted to know about evolution, and about how primitive entities inventing/discovering mathematical concepts could work, and imo many other things! Really, this didn't do very much beyond just telling me "just consider all possible universes — somewhere in there, structures occur"! Like, yes, I've been given a context in which structure-gaining happens, but this does very little to help me make sense of structure-gaining. I'd guess that knowing the "primordial human learning algorithm" which is there in a fetus is significantly more like knowing the laws of physics than your comment makes it out to be. If it's not like that, I would like to understand why it's not like that — I'd like to understand why a fetus's learning-structures really deserve to be considered the "human learning algorithm", as opposed to being seen as just providing a context in which wild structure-gaining can occur and playing some important role in this wild structure-gaining (for now).
to conclude: It currently seems unlikely to me that knowing a newborn's "primordial learning algorithm" would get me close to understanding human learning — in particular, it seems unlikely that it would get me close understanding how humanity gains scientific/mathematical/philosophical understanding. Also, it seems really unlikely that knowing this "primordial learning algorithm" would get me close to understanding learning/technology-making/mathematical-understanding-gaining in general.^[5]

like, such that it is already there in a fetus/newborn and doesn't have to be gained/built ↩︎
I think present humans have much more for doing math than what is "directly given" by evolution to present fetuses, but still. ↩︎
One attempt to counter this: "but humans could reprogram into basically anything, including whatever better system for doing math there is!". But conditional on this working out, the appeal of the claim that fetuses already have a load-bearing fixed "learning algorithm" is also defeated, so this counterargument wouldn't actually work in the present context even if this claim were true. ↩︎
let's assume this makes sense ↩︎
That said, I could see an argument for a good chunk of the learning that most current humans are doing being pretty close to gaining thinking-structures which other people already have, from other people that already have them, and there is definitely something finite in this vicinity — like, some kind of pure copying should be finite (though the things humans are doing in this vicinity are of course more complicated than pure copying, there are complications with making sense of "pure copying" in this context, and also humans suck immensely (compared to what's possible) even at "pure copying"). ↩︎

[-]TAG6mo*4-2

But there’s something else, which is a very finite legible learning algorithm that can automatically find all those things

Is there? I see a.lot of talk about brain algorithms here, but I have never seen one stated...made "legible".

—the object-level stuff and the thinking strategies at all levels. The genome builds such an algorithm into the human brain

Does it? Rationalists like to applaud such claims, but I have never seen the proof.

And it seems to work!

Does it? Even If we could answer every question we have ever posed, we could still have fundamental limitations. If you did have a fundamental cognitive deficit, that prevents you from.understanding some specific X how would you know? You need to be able to conceive X before conceiving that you don't understand X. It would be like the visual blind spot...which you cannot see!

And then I’m guessing your response would be something like: there isn’t just one optimal “legible learning algorithm” as distinct from the stuff that it’s supposed to be learning. And if so, sure

So why bring it up?

there isn’t just one optimal “legible learning algorithm”

Optimality -- doing things efficiency -- isn't the issue, the issue is not being able to do certain things at all.

I think this is very related to the idea in Bayesian rationality that priors don’t really matter once you make enough observations.

The idea is wrong. Hypotheses matter , because if you haven't formulated the right hypothesis , no amount of data will confirm it. Only worrying about weighting of priors is playing in easy mode, because it assumes the hypothesis space is covered. Fundamental cognitive limitations could manifest as the inability to form certain hypotheses. How many hypotheses can a chimp form? You could show a chimp all the evidence in the world, and it's not going to hypothesize general relativity.

Rationalists always want to reply that Solomonoff inductors avoid the problem on the basis that SIs consider "every" "hypothesis"... but they don't , several times over. It's not just that they are uncomputable, it's also that it's not know that every hypothesis can be expressed as a programme. The ability to range over a complete space does not equate to the ability to range over Everything.

Here’s an example: If you’ve seen a pattern “A then B then C” recur 10 times in a row, you will start unconsciously expecting AB to be followed by C. But “should” you expect AB to be followed by C after seeing ABC only 2 times? Or what if you’ve seen the pattern ABC recur 72 times in a row, but then saw AB(not C) twice? What “should” a learning algorithm expect in those cases? You can imagine a continuous family of learning algorithms, that operate on the same underlying principles.

A set of underlying principles is a limitation. SIs are limited to computability and the prediction of a sequence of observations. You're writing as that something like prediction of the next observation is the only problem of interest , but we don't know that Everything fits that pattern. The fact that Bayes and Solomomoff work that way is of no help, as shown above.

But within this range, I acknowledge that it’s true that some of them will be able to learn different object-level areas of math a bit faster or slower, in a complicated way, for example.

But you haven't shown that efficiency differences are the only problem. The nonexistence of fundamental no-go areas certainly doesn't follow from the existence of.efficiency differences.

, it can still figure things out with superhuman speed and competence across the board

The definition of superintelligence means that "across the board" is the range of things humans do, so if there is something humans can't do at all,an ASI is not definitionally required to be able to do it.

By the same token, nobody ever found the truly optimal hyperparameters for AlphaZero, if those even exist, but AlphaZero was still radically superhuman

The existence of superhuman performance in some areas doesn't prove adequate performance in all areas, so it is basically irrelevant to the original question, the existence of fundamental limitations in humans.

@Mateusz Bagiński

OP discusses maths from a realist perspective. If you approach it as a human construction, the problem about maths is considerably weakened...but the wider problem remains, because we don't know that maths is Everything.

this is conflating the reason for why one knows/believes P versus the reason for why P,

Of course, that only makes sense assuming realism.

@Kaarel

You are understating your own case, because there is a difference between mere infinity and All Kinds of Everything. An infinite collection of one kind of thing can be relatively tractable.

[-]Mateusz Bagiński6mo60

An idea-image that was bubbling in my mind while I was reading Note 1.

One naive definition of an infinite endeavor would be something like "a combinatorially exploded space of possible constructions/[phenomena to investigate]" where the explosion can stem from some finite set of axioms and inference rules or whatever.

I don't think this is endeavor-infinity in the sense you're talking about here. There's probably a reason you called (were tempted to call?) it an "infinite endeavor", not an "infinite domain". A domain is "just out there". An endeavor is both "out there" and in the agent doing/[participating in] the endeavor. That agent (thinker?) has a taste and applying that taste to that infinite but [possibly in a certain sense finitely specifiable/constrainable] thing is what makes it an endeavor and grants it its infinite character.

Taste creates little pockets of interestingness in combinatorially exploded stuff and those pockets have smaller pockets still; or perhaps a better metaphor would be an infinite landscape, certain parts of which the thinker's taste lights up with salience and once you "conquer" one salient location, you realize salience of other locations because you learned something in that location. Or perhaps you updated your taste, to the extent that these two are distinguishable. Or perhaps the landscape itself updated because you realized that you "just can" not assume Euclid's fifth postulate or tertium non datur or ex contradictione quodlibet and consequently discover a new way to do math: non-Euclidean geometries or new kinds of logic.

If I were to summarize my ad-hoc-y image of endeavor-infinity at the moment, it would be something like:

An infinite endeavor emerges from a thinker imposing/applying some (very likely proleptic) taste/criterion to a domain and then exploring (and continuing to construct?) that domain according to that taste/criterion's guidance; where all three of {thinker, criterion, domain} (have the potential to) grow in the process.

(which contains a lot of ad-hoc-y load-bearing concepts to be elucidated for sure)

I only read the first note and loved it. Will surely read the rest.

[-]Mateusz Bagiński6mo40

Is the infinitude of "how should one think?" the "main reason" why philosophy is infinite? Is it the main reason for most particular infinite philosophical problems being infinite? I would guess that it is not — that there are also other important reasons; in particular, if a philosophical problem is infinite, I would expect there to at least also be some reason for its infinitude which is "more internal to it". In fact, I suspect that clarifying the [reasons why]/[ways in which] endeavors can end up infinite is itself an infinite endeavor :).

Attribution is probably very (plausibly infinitely) tricky here, similar to how it's tricky to state why certain facts about mathematical structures are true while others are false. Sure, one can point to a proof of the theorem and say "That's why P is true." but this is conflating the reason for why one knows/believes P versus the reason for why P, especially when there are multiple, very different ways to prove the same proposition.^[1] Or at least that's how it feels to me.

^{^}
I don't know how often it is the case. It would be fun to see something like a distribution of proof diversity scores for some quasi-representative set of mathematical propositions where by "proof diversity" I mean something like information diameter (Li & Vitányi, Def 8.5.1).

[-]Ishual4mo20

I want to preclude scenarios which look like doing a bunch of philosophy

A (perhaps related) pathology: a mind that, whenever it sees the symbol "0", it must prove a novel theorem in ZFC in order to complete the perception of the symbol. For such a mind, many (but not all!) repetitive and boring tasks will induce an infinite endeavor (because the mind contains such an endeavor).

[-]Ishual4mo20

I think it is a mistake to think of these as finite problems^[12] — they are infinite.

It is often possible to build multiple instances of a "big/small" dichotomy, such that the theory has similar results. (e.g. [small="polynomial time"] vs [small="decidable"]).

When I imagine using your concept to think about AI, I want to say that cloning a strawberry/proving the Riemann hypothesis is a finite task that nevertheless likely implies an endeavor of a different character than [insert something you could do manually in a few months].

I wonder if the [small=finite] version of your concept is the one we should be using.

[-]Ishual4mo20

I'd maybe rather say that an infinite endeavor is one for which after any (finite) amount of progress, the amount of progress that could still be made is greater than the amount of progress that has been made, or maybe more precisely that at any point, the quantity of “genuine novelty/challenge” which remains to be met is greater than the quantity met already

[Edit: this line of reasoning is addressed later on; this comment is an artefact of not having first read the whole post, specifically see "With this picture in mind, one can see that whether an endeavor is infinite depends on one's measure "]
Imagine it makes sense to quantify the "genuine novelty" of puzzles using rational numbers, and imagine an infinite sequence of puzzles with "genuine novelty" of the i-th puzzle given {0..i-1} being equal to 1. Hence the sum of their "genuine novelty" diverges. Now, create a game which assigns 1/2^{i+1} points to solving the i-th puzzle. My guess as to the intended behaviour of your concept in this "tricky" example:
- the endeavour of maximizing the score on this game is infinite.
- the endeavour of being pretty sure to get a decent score at this game is not infinite.
- the game itself is neither necessarily finite nor infinite.
- for this game to support the weight of math/physics/cooking mushroom pies/etc..., it is not sufficient for me to become "very good at the game".
- The winner of this game is not determined by the finitude of the endeavors of the players [this is trivial, but note less trivially that for any finite number N, the prefix sequence maps to a finite endeavor, and the postfix sequence maps to an infinite endeavor with value in the game (if we let the endeavors "complete") of 1-1/2^{N}, 1/2^{N} respectively].

A different way to make the "game" a test of the concept boundary would be: you get 1 point if you give the solution to at least one of the puzzles in the infinite sequence, else you get 0 points. This game lets you trivially construct infinite endeavors, despite yielding (for every infinite endeavor X) no benefit over a finite prefix (of X). Understanding all the different ways you could have won the game is an infinite endeavor.

[-]Jonas Hallgren6mo20

There's a lot of good thought in here and I don't think I was able to understand all of it.

I will focus in on a specific idea that I would love to understand some of your thoughts on, looking at meta categories. You say something like the problem in itself will remain even if you go up a meta level. My questioning is about how certain you're of this being true? So from a category theory lens your current base-claim in the beginning looks something like:

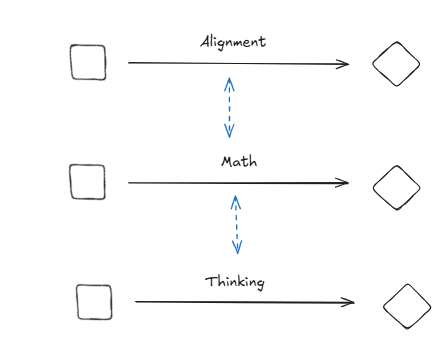
And so this is more than this, it is also about a more general meta-level thing where even if you were to try to improve this thing in itself you would get something like a mapping that involves itself? (This is a question; yes or no?)

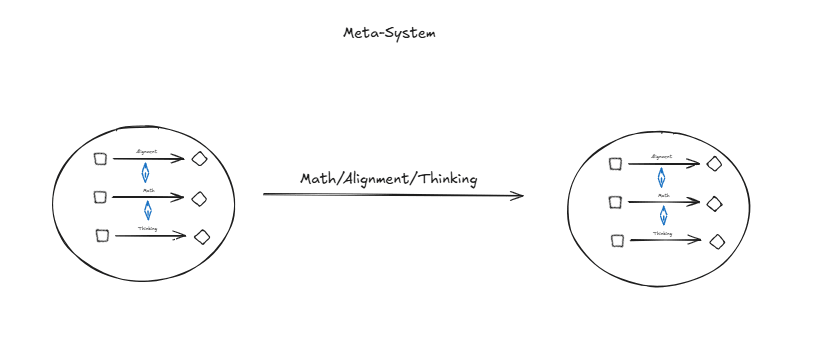
And even more generally we could then try to take the next level of this being optimised so the meta meta level:

We can go above this and say that this will happen an arbitrary amount of times. I have an hypothesis, which is that if you go up to the n-category you will start to see generalized structural properties of all of these systems that you can then use in order to say something about how individual alignment looks like. It isn't necessarily that thinking in itself won't be adapted to the specific problem at hand, it is rather that thinking might have structural similarities at different meta levels and that this can be used for alignment? Like there's design patterns to be foundn between the levels of thinking and abstraction rather than through more of them? It might just fall apart for the same reason but it seems to me like it could be an interesting area of exploration.

I don't know if this makes sense but I did enjoy this post so thank you for writing it!

[-]Kaarel6mo*10

Thank you for your comment!

What you're saying seems more galaxy-brained than what I was saying in my notes, and I'm probably not understanding it well. Maybe I'll try to just briefly (re)state some of my claims that seem most relevant to what you're saying here (with not much justification for my claims provided in my present comment, but there's some in the post), and then if it looks to you like I'm missing your point, feel very free to tell me that and I can then put some additional effort into understanding you.

So, first, math is this richly infinite thing that will never be mostly done.
If one is a certain kind of guy doing alignment, one might hope that one could understand how e.g. mathematical thinking works (or could work), and then make like an explicit math AI one can understand (one would probably really want this for science or for doing stuff in general^[1], but a fortiori one would need to be able to do this for math).^[2]
But oops, this is very cursed, because thinking is an infinitely rich thing, like math!
I think a core idea here is that thinking is a technological thing. Like, one aim of notes 1–6 (and especially 3 and 4) is to "reprogram" the reader into thinking this way about thinking. That is, the point is to reprogram the reader away from sth like "Oh, how does thinking, the definite thing, work? Yea, this is an interesting puzzle that we haven't quite cracked yet. You probably have to, like, combine logical deduction with some probability stuff or something, and then like also the right decision theory (which still requires some work but we're getting there), and then maybe a few other components that we're missing, but bro we will totally get there with a few ideas about how to add search heuristics, or once we've figured out a few more details about how abstraction works, or something."
Like, a core intuition is to think of thinking like one would think of, like, the totality of humanity's activities, or about human technology. There's a great deal going on! It's a developing sort of thing! It's the sort of thing where you need/want to have genuinely new inventions! There is a rich variety of useful thinking-structures, just like there is a rich variety of useful technological devices/components, just like there is a rich variety of mathematical things!
Given this, thinking starts to look a lot like math — in particular, the endeavor to understand thinking will probably always be mostly unfinished. It's the sort of thing that calls for an infinite library of textbooks to be written.
In alignment, we're faced with an infinitely rich domain — of ways to think, or technologies/components/ideas for thinking, or something. This infinitely rich domain again calls for textbooks to keep being written as one proceeds.
Also, the thing/thinker/thought writing these textbooks will itself need to be rich and developing as well, just like the math AI will need to be rich and developing.
Generally, you can go meta more times, but on each step, you'll just be asking "how do I think about this infinitely rich domain?", answering which will again be an infinite endeavor.
You could also try to make sense of climbing to higher infinite ordinal levels, I guess?

(* Also, there's something further to be said also about how [[doing math] and [thinking about how one should do math]] are not that separate.)

I'm at like inside-view p=0.93 that the above presents the right vibe to have about thinking (like, maybe genuinely about its potential development forever, but if it's like technically only the right vibe wrt the next years of thinking (at a 2024 rate) or something, then I'm still going to count that as thinking having this infinitary vibe for our purposes).^[3]

However, the question about whether one can in principle make a math AI that is in some sense explicit/understandable anyway (that in fact proves impressive theorems with a non-galactic amount of compute) is less clear. Making progress on this question might require us to clarify what we want to mean by "explicit/understandable". We could get criteria on this notion from thinking through what we want from it in the context of making an explicit/understandable AI that makes mind uploads (and "does nothing else"). I say some more stuff about this question in 4.4.

if one is an imo complete lunatic :), one is hopeful about getting this so that one can make an AI sovereign with "the right utility function" that "makes there be a good future spacetime block"; if one is an imo less complete lunatic :), one is hopeful about getting this so that one can make mind uploads and have the mind uploads take over the world or something ↩︎
to clarify: I actually tend to like researchers with this property much more than I like basically any other "researchers doing AI alignment" (even though researchers with this property are imo engaged in a contemporary form of alchemy), and I can feel the pull of this kind of direction pretty strongly myself (also, even if the direction is confused, it still seems like an excellent thing to work on to understand stuff better). I'm criticizing researchers with this property not because I consider them particularly confused/wrong compared to others, but in part because I instead consider them sufficiently reasonable/right to be worth engaging with (and because I wanted to think through these questions for myself)! ↩︎
I'm saying this because you ask me about my certainty in something vaguely like this — but I'm aware I might be answering the wrong question here. Feel free to try to clarify the question if so. ↩︎

[-]Ishual4mo10

With this picture in mind, one can see that whether an endeavor is infinite depends on one's measure — and e.g. if all you're interested in in mathematics is finding a proof of some particular single theorem, then maybe "math" seems finite to you.

Informally and intuitively, securing the future (in a conflict) naturally induces a measure that makes math seem finite, but enjoying the future (after you have somewhat secured it) naturally induces a measure that makes math seem infinite.

[-]Ishual4mo10

If is an infinite endeavor, then "how should one do $E$ ?" is also infinite.^[18] For example: math is infinite, so "how should one do math?" is infinite; ethics is infinite, so "how should one do ethics?" is infinite.^[19]
If $E$ is an infinite endeavor and there is a "faithful reduction" of $E$ to another endeavor $F$ , then $F$ is also infinite. (In particular, if an infinite endeavor $E$ is "faithfully" a subset of another endeavor $F$ , then $F$ is also infinite.)^[20] For example, math being infinite implies that stuff in general is infinite; "how should one do math?" being infinite implies that "how should one think?" is infinite.
If an endeavor constitutes a decently big part of an infinite endeavor, then it is infinite.^[21]^[22] For example, to the extent that language is and will remain to be highly load-bearing in thinking, [figuring out how thinking should work] being infinite implies that [figuring out how language should work] is also infinite.

Important and useful, but also keep in mind:
a'. If "how should one do E?" is a finite endeavor then E is finite.
b'. If F finite, then any E that reduces to F must also be finite.
c'. If an endeavor contains not too much more than a finite endeavor, then it is finite.

perhaps "infinitude clusters"? perhaps "infinitudes don't exist alone?" perhaps "infinitudes are not isolated?" perhaps "non-solitary infinitudes?"

1 thinking can only be infinitesimally understood^[10]

The following questions about thinking are sometimes conceived of as ones to which satisfactory answers could be provided (in finite time)^[11]:

"What's intelligence?"
(a probably better version of the above:) "How does thinking work?"
(a probably still better version of the above:) "How should one think?"

I think it is a mistake to think of these as finite problems^[12] — they are infinite.

We can define a "complexity class" of those endeavors which are infinite; I claim the following are some central endeavors in this class: figuring out math, understanding intelligence, and inventing all useful technologies.^[13]

Why are these three endeavors infinite? The next two notes will (among other things) provide an argument that if one of these endeavors is infinite, then so are the other two. And I will assert without providing much justification (here) that math is infinite.

What do I mean by an infinite endeavor? I could just say "an endeavor such that any progress that could be made (in finite time) [won't be remotely satisfactory]/[won't come remotely close to resolving the matter]". I'd maybe rather say that an infinite endeavor is one for which after any (finite) amount of progress, the amount of progress that could still be made is greater than the amount of progress that has been made, or maybe more precisely that at any point, the quantity of “genuine novelty/challenge” which remains to be met is greater than the quantity met already.

Hmm, but consider the endeavor of pressing a button very many times in some setup which forces you into mindlessness about how you are to go about getting the button pressed very many times — maybe you wake up each morning in a locked room with only a button in it, getting rewarded one util (whatever that means) for each day on which you press the button, maybe with various other constraints that make it impossible for you to make an art out of it or take any kind of rich interest in it beyond your interest in goodness-points or really think about it much at all — basically, I want to preclude scenarios which look like doing a bunch of philosophy about what it is for something to be "that button" and what it is for that button to "be pressed" and what "a day" is and developing tech/science/math/philosophy around reliably getting the button pressed and so on. Are we supposed to say that pressing the button many times is an infinite endeavor for you, because there is always more left to do than has been done already?
I want to say that pressing the button many times (given the setup above) is not an infinite endeavor for you — I want to say that largely because that conflicts with my intuitive notion of an infinite endeavor and because it makes at least one thing I'd like to say later false. I might be able to get away with saying it is not infinite because it only presents a small amount of genuine novelty/challenge, saying that we should go with the last definition in the superitem (i.e., the parent item to this item on this list), but I'm sort of unhappy with the state of things here.
This button example makes me consider changing the definition of an infinite endeavor to be the following: an infinite endeavor is one which cannot be finitely well-solved/finished on any meta-level — i.e., it itself cannot be remotely-well-[solved/finished], and figuring out how to go about working on it cannot be remotely-well-[solved/finished], and figuring out how to go about that cannot be remotely-well-[solved/finished] either, and so on.
1. Actually, it should be fine to just require that the meta-[problem/endeavor] cannot be remotely-well-[solved/finished] — i.e., that there is no $[\geq some positive const]$ -satisfactory finite protocol for the object-[problem/endeavor], because I think this would imply that the object-endeavor itself cannot be remotely-well-finished (else we could have a finite protocol for it: just provide the decent finite solution) and that the higher meta-endeavors cannot be remotely-well-finished either (because finitely remotely-well-finishing a higher meta-endeavor would in particular provide a finite protocol for the object-endeavor).

We could speak instead of "practically infinite endeavors" — endeavors for which for any amount of progress one could ever make on the endeavor in this universe, the importance-weighted-quantity of "stuff" which is not yet figured out will be greater than the importance-weighted-quantity of "stuff" which has been figured out. That an endeavor is practically infinite is [a weaker assertion than that it is infinite], and we could retreat to those assertions throughout these notes — such claims would be sufficient to support our later assertions. Actually, we could probably even retreat to the weaker assertions still that certain endeavors couldn’t be remotely finished in (say) 1000 years of humans doing research. But going with the riskier claim seems neater.

If you conceive of making progress on an endeavor as collecting pieces with certain masses in

R_{\geq 0}

and only being able to collect finitely many pieces in any amount of time, then you should imagine the sum of the masses of all pieces being infinite for an infinite endeavor.

With this picture in mind, one can see that whether an endeavor is infinite depends on one's measure — and e.g. if all you're interested in in mathematics is finding a proof of some particular single theorem, then maybe "math" seems finite to you. For these notes, I want to get away with just saying we're measuring progress in some intuitive way which is like what mathematicians are doing when saying math is infinite, marking the question of how to think of this measure as an important matter to resolve later. For example, maybe it would be natural to make the measure time-dependent (that is, changing with one’s current understanding), since it might be natural for what is potentially important (as progress? or for making progress?) to depend on where one is?
I should clarify that there is a different conception of an infinite endeavor as one in which there is an infinite amount to do in a much weaker sense, such that there is some sort of convergence toward having finished the endeavor anyway. In this picture where one is collecting pieces, this is like there being infinitely many pieces, but with the sum of all their masses being finite, so even though one can only collect finitely many pieces by any finite time, one can see oneself as getting arbitrarily close to having solved the problem. And I want to clarify that this is not what I mean when I say an endeavor is infinite — I mean that it is much more infinite than this!

Generally, given some reasonable and/or simplifying assumptions, it should be equivalent to say that an infinite endeavor is one in which there is an infinite amount of cool stuff to be understood (whereas (by any finite time) one could only ever understand a finite amount). Given some assumptions, it should also be equivalent to say that an infinite endeavor is one which presents infinitely many challenges of at least some constant significance/importance (in the above picture with pieces, one should be allowed to merge pieces into one challenge to have that equivalence work out).

An infinite endeavor can only be infinitesimally completed/solved.

If we were to make the measure time-dependent, I’d maybe instead want to say “an infinite endeavor can only be (let’s say) $[\leq \frac{1}{3}]$ -completed/solved”, and maybe instead call it a forever-elusive/slippery/escaping question/quest/problem/endeavor. Maybe I should be more carefully distinguishing quests/questions/problems from corresponding pursuits/endeavors-to-address/solutions — I could then speak here of, say, it being an infinite endeavor to handle/address an elusive question. Anyway, a problem continuing to slip away in this sense wouldn’t imply that it is at each time only infinitesimally solved according to the measure appropriate to that same time, though it would of course still imply that the problem will always seem mostly unsolved, and it would (given some fairly reasonable assumptions) also imply that for each state of understanding, there is another (more advanced) state of understanding from the vantage point of which the fraction of progress which had been made by the earlier state is arbitrarily close to $0$ .

Math is infinite.

I should say more about what I mean by this. For math in particular, I want to claim that always, the total worth/significance/appeal of theorems not yet proven will be greater than the total worth/significance/appeal of theorems already proven, the total worth/significance/appeal of objects not yet discovered/identified/specified/invented will be greater than the total worth/significance/appeal of objects not yet discovered/identified/specified/invented, and analogously for proof ideas and for broad organization (and maybe also some other things).
Like, I think that when one looks at math now, one gets a sense that there's so much more left to be understood than has been understood already, and not in some naive sense of there having been only finitely many propositions proved of the infinitely many provable propositions, but in a much more interesting significance-weighted sense; my claim is that it will be like this forever.^[14]
an objection: "Hmm, but isn't there a finite satisfactory protocol for doing math, because something like the present state of this universe could plausibly be finitely specified and it will plausibly go on to "do math" when time-evolved satisfactorily? (And one could make something with a much smaller specification that still does as well, also.) We could plausibly even construct a Turing machine "doing roughly at least as much math" from it? So isn't math finite according to at least one of the earlier definitions?"
1. my response: If it does in fact get very far in math (which is plausible), it would be a forever-self-[reprogramming/reinventing] thing, a thing indefinitely inventing/discovering and employing/incorporating new understanding and new ways of thinking on roughly all levels. I wouldn't consider it a fixed protocol (though I admit that this notion could use being made more precise).^[15]
It would be good to more properly justify math being infinite (which could benefit from the statement being made more precise (which would be good to do anyway)); while Note 2 and Note 3 will provide some more justification (and elaboration), I’m far from content with the justification for this claim provided in the present notes.

"How should one think?" is as infinite as mathematics (I'll provide some justification for this in the next few notes), so the endeavor to understand thinking will only ever be infinitesimally finished. Much like there's no "grand theorem/formula of mathematics" and there's no "ultimate technology (or constellation of technologies)", there's no such thing as a (finite) definitive understanding of thinking — understanding how thinking works is not a problem to be solved.

"How does thinking work?" should sound to us a lot like "how does [the world]/everything work?" (asked in the all-encompassing sense^[16]) or "how does doing stuff work?". I hope to impart this vibe further and to make the sense in which these should sound alike more precise with the next three notes.

All that said, this is very much not to say that it is crazy to work on understanding thinking. It's perfectly sensible and important to try to understand more about thinking, just like it's perfectly sensible and important to do math. Generally, we can draw a bunch of analogies between the character of progress in math and the character of progress in understanding thinking.

In both math and investigating thinking, progress on an infinite thing can still be perfectly substantive.^[17] A mathematical work can be perfectly substantive despite being an infinitesimal fraction of all of math.
It can still totally make sense to try to study problems about intelligence which relate to many aspects of it, much like it can make sense to do that in math.
It can still totally make sense to prefer one research project on thinking to another — even though each is an infinitesimal fraction of the whole thing, one can still easily be much greater than the other.
However, working on finding and understanding the structure of intelligence in some definitive sense is like working on finding "the grand theorem of math" or something.

I'm very much not advocating for quietude on an endeavor in response to its infinitude. I think there are many infinite endeavors which merit great effort, and understanding thinking is one of them. In fact, understanding thinking is probably a central quest for humanity and pretty much all minds (that can get very far)!

One could object to my claim that "I will understand intelligence, the definite thing" is sorta nonsense by saying "look, I'm not trying to understand thinking-the-infinite-thing; I'm trying to understand thinking as it already exists in humans/humanity/any-mind-that's-sorta-smart, which is surely a finite thing, and so we can hope to pretty completely understand it?". I think this is pretty confused. I will discuss these themes in Note 4.

And again, I think it is perfectly sensible and good to study intelligence-the-thing-that-already-exists-in-humans (for example, as has already been done by philosophers, logicians, AI researchers, alignment researchers, mathematicians, economists, etc.); I just think it is silly to be trying to find some grand definitive formula for it (though again, it totally makes sense to try to say broad things that touch many aspects of intelligence-the-thing-that-already-exists-in-humans, just like it makes sense to try to do something analogous in math).

2 infinitude spreads

An endeavor being infinite often causes other related endeavors to be infinite. In particular:

If $E$ is an infinite endeavor, then "how should one do $E$ ?" is also infinite.^[18] For example: math is infinite, so "how should one do math?" is infinite; ethics is infinite, so "how should one do ethics?" is infinite.^[19]
If $E$ is an infinite endeavor and there is a "faithful reduction" of $E$ to another endeavor $F$ , then $F$ is also infinite. (In particular, if an infinite endeavor $E$ is "faithfully" a subset of another endeavor $F$ , then $F$ is also infinite.)^[20] For example, math being infinite implies that stuff in general is infinite; "how should one do math?" being infinite implies that "how should one think?" is infinite.
If an endeavor constitutes a decently big part of an infinite endeavor, then it is infinite.^[21]^[22] For example, to the extent that language is and will remain to be highly load-bearing in thinking, [figuring out how thinking should work] being infinite implies that [figuring out how language should work] is also infinite.

Thinking being infinite can help make some sense of many other philosophical problems/endeavors being infinite.^[23]

Specifically:
1. If "solving" a philosophical problem would entail understanding some aspect of thinking which has a claim to indefinitely constituting a decently big part of thinking, then
2. If "solving" a philosophical problem would entail making a decision on [how one's thinking operates in some major aspect], that philosophical problem is not going to be remotely "solved", because one will probably want to majorly change how one's thinking works in that major aspect later.
Here are some problems whose infinitude could be explained by the infinitude of thinking in this way (but whose infinitude could also be explained in other ways):
1. "how does learning work?"
2. “how does language work?”
3. "how should one assign probabilities?"
4. “what are concepts? which criteria determine whether concepts are good?”
5. "how does science work?"
6. "how should one do mathematics?"
7. "what is the character of value(ing)?"
You might feel indifferent about some of these problems; you could well have a philosophical system in which some of these are not load-bearing (as I do). My claim is that those problems which are genuinely load-bearing in your philosophical system are probably infinite, and their infinitude can be significantly explained by the infinitude of "how should one think?".
We could imagine a version of these problems which could be solved — for example, one might construct a GOFAI system which has a (kinda-)language+meaning which is plausibly load-bearing for it but which will not be reworked. My claim is that for a mind which will indefinitely be thinking better, if it has "language" and "meaning", to the extent these are load-bearingly sticking around indefinitely, the mind will also "want to" majorly rework them indefinitely.
Again, all this is very much not to say that one cannot make progress on these philosophical problems — even though any progress will be infinitesimal for these infinite endeavors, one can make substantive progress on them (just like one can make substantive progress in math), and I think humanity is in fact continuously making substantive progress on them. So, for many philosophical problems/endeavors $P$ , I can get behind “we’re pretty much no closer to solving $P$ now than we were 2000 years ago” — meaning that only an infinitesimal fraction has been solved, just like earlier, or that only a finite amount has been figured out, with a real infinity still remaining, just like earlier — while very much disagreeing with the possible followup “that is, we haven’t made any progress on $P$ since 2000 years ago” — I think probably more than half of the philosophical progress up until now happened since 1700, and maybe even just since 1875.^[24]

Saying these problems are infinite because of the infinitude of "how should one think?" can make it seem like we are viewing ourselves very much "from the outside" when tackling these problems and when tackling "how should one think?", but I also mean to include tackling these problems more "from the inside".

What do I mean by tackling these problems "from the outside" vs "from the inside"? Like, on the extreme of tackling a problem "from the outside", you could maybe imagine examining (yourself as) another thinking-system out there, having its language and beliefs and various thought-structures somehow made intelligible to you, with you trying to figure out what eg its concept of "existence" should be reworked to. Tackling "the same problem" from the inside could look like having various intuitions about existence and trying to find a way to specify what it means for something to exist in terms of other vocabulary such that these intuitions are met (this can feel like taking "existence" to already be some thing, just without you having a clear sense of what it is). And a sorta intermediate example: asking yourself why you want a notion of "existence", trying to answer that by examining cases where your actions (or thinking more broadly) would depend on that notion, and seeking to first make sense of how to operate in those cases in some way that routes through existence less. Of course, in practice, we always have/do an amalgam of the inside and outside thing.^[25]
I'm saying that the infinitude of [such investigations which are more from the inside of a conceptual schema] could also be partly explained by the infinitude of "how should thinking work?".^[26]

Wanting to rework one's system of thought indefinitely is also a reason for keeping constituent structures provisional.

3 math, thinking, and technology are equi-infinite

If one of math, understanding intelligence, and inventing useful technologies is infinite, then so are the other two. (An argument for this is given in items 2–6 of this list.)

So, if you think any one of the three is infinite, then you should also think that the other two are. In particular, if you're on board with my earlier assertion that math is infinite, then you should also agree that thinking and technology are infinite. Or you could prima facie buy into technology being infinite, and get to thinking that thinking and math are infinite from there.

If math is infinite, then "how should one do math?" is infinite.

I could just appeal to note 2 item 1.1 to justify this, but it makes sense to also justify this independently (especially given that I haven't justified 2.1.1 well). (Also, if we went with the definition of an infinite endeavor in 1.4.3(.1), then we'd be done by definition here, but that's not too exciting, either.)
I guess I'd first like to try to get you to recognize that if you accepted my earlier assertion that math is infinite, then you might have already sorta accepted that doing math is infinite, at least in the following sense:
1. If we think of math-the-more-object-level-endeavor as being ultimately about printing proofs of propositions, then we should plausibly already think of say, mathematical ideas (e.g., the idea of a probabilistic construction) or mathematical objects/constructions (e.g., a vector space) or frames/arenas organizing mathematical fields (e.g., the scheme-theoretic organization of algebraic geometry) as meta-level things — they are like tools one uses to print proofs better.
2. This isn't to say that math is in fact ultimately well-thought-of as not also being about defining objects and coming up with new ideas and so on. But I want to get across the sense that these live in significant part also on the meta-level — that they are not just things in the object-domain, but also components of us doing math. Getting further in math centrally involves gaining these tools, from others or by making them yourself.^[27]
Quite generally, given that understanding a domain better blends together with thinking better in the domain to a significant extent, if you think there's an infinitely rich variety of things to understand in mathematics, this gives you some reason to think that there is also an infinitely rich variety of structure to employ in doing mathematics, so it gives you some reason to think that figuring out how one should do math is an infinite endeavor.

If "how should one do math?" is infinite, then "how should one think?" is also infinite.

We could just say this is a special case of 2.1.2 (i.e., item 1.2 from Note 2), but it also makes sense to justify this separately/again. I think it'd be super bizarre for mathematical thinking and thinking in general not to be equi-infinite; it'd be particularly bizarre for getting better at thinking to be infinitely "easier" than getting better at mathematical thinking. They are just way too similar (in the relevant aspect(s)). It's not like math researchers use thinking in some profoundly different class when doing math (compared to when doing other thinking). Things in general are way too much like math way too much of the time. Doing things in general involves doing math way too centrally.

If "how should one think?" is infinite, then tech is also infinite.

The question "how should one think?" is/[centrally involves] the question "which thinking-[structures/technologies] should one make/use?", so this latter question is then also infinite (maybe by 2.1.3). And "thinking-technologies" are ("faithfully") a subset of all technologies, so tech is also infinite by 2.1.2.^[28]

Finally, if tech is infinite, then math is infinite.

The vibes are very similar, in the relevant way.
In particular, technological objects are a lot like mathematical objects. From this, one might think that tech is like a fragment of math, in which case one might think that math could only be more infinite than tech, appealing to 2.1.2.
But also, our mathematical ideas "show up load-bearingly" all over the place in our technologies, so one could try to see math as a fragment of tech and to infer its infinitude from the infinitude of tech using 2.1.3.
Actually, our math just is one kind of tech we're building (for our thinking and also for other doings) — this gives another way to see math as a subendeavor of tech for us, and one can then again try to infer its infinitude using 2.1.3.
Additionally, math shows up load-bearingly in developing tech, so one could infer the infinitude of developing tech from the infinitude of tech using 2.1.1 and then infer the infinitude of math from that using 2.1.3.
Let us say more about math and tech having similar vibes (in the relevant way). One could tell many stories to communicate that the vibes are similar; here are the premises of a few:
1. Mathematical objects are often invented/discovered to do things, to [participate in]/support/[make possible] our (mathematical) activities, and to help us with problems/projects — just like (other) technological objects.
2. One can think of a technology in terms of its construction/composition/design/[internal structure], like an engineer might, or one can think of a technology in terms of [its function(s)]/[its purpose(s)]/[what one can do with it]/[how to use it]/[what it is like as it operates]/[its properties]/[how it relates to other things]/[the surrounding external structure]^[29], like one usually does when thinking about doing stuff with the technology. This is also true of mathematical devices — for example, one can think of the real numbers in terms of their construction (e.g. as Cauchy sequences of rationals^[30] or Dedekind cuts of rationals), or one can instead think of the real numbers as a complete ordered field, or as being involved in geometry and analysis in various ways, etc.; one can think of the homology groups of a topological space in terms of their construction (e.g. via the simplicial route or the singular route), or one can instead think of homology groups as things of which the various theorems in Hatcher involving homologies are true (indeed, one can pin down the homology of a space uniquely as the thing satisfying some axioms — see Section 2.3 and Theorem 4.59 in Hatcher^[31]); one can think of a product of topological spaces as having tuples as points and having its topology generated by cylinder sets, or as a canonical topological space equipped with continuous maps to the original spaces.
3. One can also just be using a technology without thinking about it much (for example, you can be using your laptop to write notes without thinking about your laptop much), and one can also be using a mathematical thing in one's thinking without thinking about it much (for example, you can be doing stuff with real numbers without explicitly thinking about how their construction or even their properties). (However, a difference: there is structure supporting/[involved in] your use of your laptop which lives outside your head, whereas the structure involved in your use of a vector space lives $\approx$ entirely in your head.)

Note that the implications about infinitude in items 2-5 on this list form a loop, so we've provided an argument that these endeavors are equi-infinite. More precisely, we've given an argument that if any one of these problems/endeavors is infinite, then any other is also infinite; this means that they are either all finite or all infinite.^[32]

You might say: “Okay, I agree that there’s a genuine infinity of mathematical objects (and so on), a genuine infinity of technologies, and a genuine infinity of thinking-technologies in particular. But couldn’t there be a level above all these infinite messes where there’s some simple thing?”. My short answer is: no, e.g. our handling of mathematical objects is technological/organic throughout. A longer answer:

For example, let's look at making concepts.^[33] Making concepts looks e.g. like having a varied system for morphological derivation and inflection, giv-ing parti-cul-ar ab(i)-(bi)li(s)-ti-es to pro-duce con-cep-t-s. Here are some more example high-level ways in which new concepts can be found:
1. become familiar with many toy cases; push yourself to see them as clearly as possible; if any objects show up, try to see if they can also be used in other contexts;
2. when you have a toy setting worked out, ask what "auxiliary constructions"/"nontrivial ideas" were involved^[34];
3. generalize existing things; unify existing things; articulate similarities; find what's responsible for similarities;
4. make existing looser notions more precise; make distinctions;
5. get concepts for a novel context via analogy to some familiar context;
6. look for a thing which would "work" a certain way; look for a thing which would play a certain role^[35];
7. more generally, have some constraints on a hypothetical thing in mind and look for a concrete thing which would satisfy those constraints;
8. in particular, for various particular relations or functions, look for what stands in that relation with some thing or what that function takes some thing to;
9. in particular, look for the (logical) cause of some property or event;
10. look for ways you can relate something to other things; look for things you can do with it; look for ways to transform it;
11. enumerate all things of some kind and see if any are useful.
Making concepts can look a lot like making (more explicit) technologies, in which surely very much of our thinking is importantly involved.
Also, I'd sorta object to thinking there is a level "above" this messy world of concepts. There are surely structures present in us-doing-math beyond easily visible mathematical concepts, including structures of different kinds, but instead of thinking of these structures as handling and organizing concepts from above, I think it's better to think of the whole thinking-shebang as like an organic thing, so this sounds e.g. like thinking that [blood circulation]/[the cardiovascular system] is a structure "above" the organs, or like saying a tree is a structure organizing koalas. Additionally, the structure surrounding a concept is in significant part [given by]/[made of] other concepts.
You might say: "hmm, you're talking about all these things we can easily see, but couldn't there be a nice hidden structure which handles things? like, a structure in the brain?".
1. Well, I certainly have been talking about those things we can see better, and there are surely many structures in our thinking-activities^[36] that we can't see that clearly at present. It seems unlikely that there'd be these central hidden things of a fundamentally different character than the various technological things we can see, though.
You might say: "hmm, maybe thinking is this organic-technological mess now, but couldn't it become well-organized? couldn't there be some sort of formula for thinking which remains to be discovered/reified?". Or maybe you might say: "hmm, maybe thinking is an organic-technological mess, but couldn't it really be a shadow of a very nice thing?"
1. There are surely nice things shadowed in thinking. For example, (almost all) clear human mathematical statements and clear mathematical proofs (especially from after like 1950 or whatever) have formal counterparts in ZFC — there's a very real "near-isomorphism" of an important thing in human mathematical (thinking-)activities with a nice formal thing. For another example, there are ways to see bayesianism (usually combined with other interesting "ideas") in various things from (frequentist) statistical methods to plant behavior^[37]. It can often be helpful to understand something about the actual thing by evoking the nice thing; it is in some contexts appropriate to think almost entirely about a nice thing to figure out something about the actual thing. But I think there are very many nice things shadowed in thinking, with developing thinking continuing to shadow more cool things on all levels indefinitely.
2. This seems close to asking whether the (technological) world would eventually just "have" one kind of thing. And it seems unlikely that it would!
3. There will probably continue to be a very rich variety of (thinking-)structures in use.
4. If I had to guess at some single higher "structure" centrally "behind/in" thinking, I'd say "one is creative; one finds/invents and finds uses for (thinking-)structures".^[38] But I don't think this is some sort of definite/simple thing — I think this will again be rich, involving many "ideas".
5. I've tried to say more in response to these questions in the next few notes.

4 general intelligence is not that definite

In note 1, I claimed that "I will get some remotely definitive understanding of problem-solving" is sorta nonsense like "I will solve/[find a grand theor[y/em] for] math" or "I will conceive of the ultimate technology". One could object to this by saying "look, I'm not trying to understand intelligence-the-infinite-thing; I'm trying to understand intelligence as it already exists in humans/humanity/any-one-particular-mind-that's-sorta-generally-intelligent, which is surely a finite thing, and so we can hope to pretty completely understand it?". I think this is still confused; here's my response:

Intelligence in humans/humanity/any-reasonable-mind-that's-sorta-smart will already be a very rich thing. Humans+humanity+evolution has already done very much searching for structures of thinking, and already found and put to use a great variety of important ones.
1. [Humans are]/[humanity is] self-reprogramming. (Human self-reprogramming needn't involve surgery or whatever.) A central example: [humans think]/[humanity thinks] in language(s), and humans/humanity made language(s) — in particular, we made each word in (each) language.^[39] Humanity is amassing an arsenal of mathematical concepts and theorems and methods and tricks. We make tools^[40], some of which are clearly [parts of]/[used in]/[playing a role in] thinking, and all of which^[41] have been involved in us doing very much in the world. We learn how to think about various things and in various ways; when doing research, one thinks about how to think about something better all the time. I'm writing these notes in large part to restructure my thinking (and hopefully that of some others) around thinking and alignment^[42] (as opposed to like, idk, just stating my yes/no answers to some previously well-specified questions (though doing this sort of thing could also totally be a part of improving thinking)).
Anyway, yes, it's probably reasonable to say that humanity-now has some finite (but probably "big") specification. (Moreover, I'm pretty sure that there is a 1000-line python program such that running that program on a 2024 laptop with internet access would start a "process" which would fairly quickly take over the world and lead to some sort of technologically advanced future (like, with most of the compute used being on the laptop until pretty late in the part of the process until takeover).) Unfortunately, understanding a thing is generally much harder than specifying it. Like, consider the humble cube^[43]. Is it obvious to you that its symmetry group (including rotations only, i.e., only things you can actually do with a solid physical cube) is $S_{4}$ , the permutation group on $4$ elements?^[44] Or compare knowing the weights of a neural net to understanding it.
The gap between specifying a thing and understanding it is especially big when the thing is indefinitely growing, indefinitely self-[reworking/reprogramming/improving] (as [humans are]/[humanity is]).
Obviously, the size of the gap between the ability to specify a thing and understanding it depends on what we want from that understanding — on what we want to do with it. If all we wanted from this "understanding" was to, say, be able to print a specification of the thing, then there would not be any gap between "understanding" the thing and having a specification of it. Unfortunately, when we speak of understanding intelligence, especially in the context of alignment, we usually want to understand it in its long-term unfolding,^[45] then there's a massive gap — for an example, consider the gap between having the positions and momenta of atoms when evolution got started in front of you^[46] vs knowing what "evolution will be up to" in billions of years.
And even in this cursed reference class of comprehending growing/structure-gaining things in their indefinite unfolding, comprehending a thinking thing in its unfolding has a good claim to being particularly cursed still, because thinking things have a tendency to be doing their best to "run off to infinity" — they are actively (though not always so explicitly) looking for new better ways to think and new thinking-structures to incorporate.

Relatedly: one could try to conceive of the ability to solve problems in general as some sort of binary-ish property that a system might have or might not have, and I think this is confused as well.

I think it makes much more sense to talk loosely about a scale of intelligence/understanding/capability-to-understand/capability/skill, at least compared to talking of a binary-ish property of general problem-solving. While this also has limitations, I'll accept it for now when criticizing viewing general intelligence as a binary-ish thing. (I'm also going to accept something like the scalar view more broadly for these notes, actually.^[47])
Given such a scale of intelligence, we could talk of whether a system has reached some threshold in intelligence, or some threshold in its pace of gaining intelligence. We could maybe talk of whether a system has developed some certain amount of technology (for thinking), or whether its ability to develop technology has reached a certain level.
We could talk of whether it has put to use in/for its doing/thinking/fooming^[48] some certain types of structures.
But it seems hard to make a principled choice of threshold or of structures to require. Like, there's an ongoing big foom which keeps finding/discovering/inventing/gaining new (thinking-)structures (and isn't anywhere close to being done — the history of thought is only just getting started^[49]). Where (presumably before humanity-now) would be a roughly principled place to draw a line?
1. One could again try to go meta when drawing a line here, saying it's this capacity to incorporate novel structures itself which makes for an intelligent thing. But this will itself again be a rich developing thing, not a definite thing. In fact, it is not even a different thing from [the thought dealing (supposedly) with object-level matters] for which we just struggled to draw a line above. It's not like we think in one way "usually", and in some completely different way when making new mathematical concepts or inventing new technologies, say — the thinking involved in each is quite similar. (Really, our ordinary thought involves a great deal of "looking at itself"/reflection anyway — for instance, think of a mathematician who is looking at a failed proof attempt (which is sorta a reified line of thought) to try to fix it, or think of someone trying to find a clearer way to express some idea, or think of someone looking for tensions in their understanding of something, or think of someone critiquing a view.)

One (imo) unfortunate line of thinking which gets to thinking of general intelligence as some definite thing starts from noticing that there are nice uncomputable things like kolmogorov complexities, solomonoff induction (or some other kind of ideal bayesianism), and AIXI (or some other kind of ideal expected utility maximization), and then thinks it makes sense to talk of "computable approximations" of these as some definite things, perhaps imagining some actual mind already possessing/being a “computable approximation” of such an uncomputable thing.

I think this is like thinking some theorem is "an approximate grand formula for math".
It is also like thinking that a human mathematician proving theorems is doing some “computable approximation” of searching through all proofs. A human mathematician is really “made of” many structures/[structural ideas].
More generally, the actual mind will have a lot of structure which is not remotely well-described by saying it's a computable approximation of an infinite thing. (But also, I don’t mean to say that it is universally inappropriate to draw any analogy between any actual thing and any of these infinitary things — there are surely contexts in which such an analogy is appropriate.)
For another example of this, an "approximate universal prediction algorithm" being used to predict weather data could look like humans emerging from evolution and doing philosophy and physics and inventing computers and doing programming and machine learning, in large part by virtue of thinking and talking to each other in language which is itself made of very many hard-won discoveries/inventions (e.g., there are some associated to each word), eventually making good weather simulations or whatever — there's very much going on here.
Thinking of some practical string compression algorithm as a computable approximation to kolmogorov compression is another example in the broader cluster. Your practical string compression algorithm will be "using some finite collection of ideas" for compressing strings, which is an infinitesimal fraction of "the infinitely many ideas which are used for kolmogorov compression".

One more (imo) mistake in this vicinity: that one could have a system impressively doing math/science/tech/philosophy which has some fixed “structure”, with only “content” being filled in, such that one is able to understand how it works pretty well by knowing/understanding this fixed structure. Here's one example of a system kinda "doing" math which has a given structure and only has "content" being "learned": you have a formal language, some given axioms, and some simple-to-specify and simple-to-understand algorithm for assigning truth values^[50] to more sentences by making deductions starting from the given axioms^[51]. Here's a second example of a system with a fixed structure, with only content being filled in: you have a "pre-determined world modeling apparatus" which is to populate a "world model" with entities (maybe having mechanisms for positing both types of things and also particular things) or whatever, maybe with some bayesianism involved. Could some such thing do impressive work while being understandable?

I think that at least to a very good approximation, there are only the following two possibilities here: either (a) the system will not be getting anywhere (unless given much more compute than could fit in our galaxy) — like, if it is supposed to be a system doing math, it will not actually produce a proof of any interesting open problem or basically any theorem from any human math textbook (without us pretty much giving it the proof) — or (b) you don't actually understand the working of the system, maybe wrongly thinking you do because of confusing understanding the low-level structure of the system with understanding how it works in a fuller sense. Consider (again) the difference between knowing the initial state and transition laws of a universe and understanding the life that arises in it (supposing that life indeed arises in it), or the difference between knowing the architecture of a computer + the code of an AI-making algorithm run on it and understanding the AI that emerges. It is surely possible for something that does impressive things in math to arise on an understood substrate; my claim is that if this happens, you won't be understanding this thing doing impressive math (despite understanding its substrate).
Let us focus on systems doing math, because (in this context), it is easier to think about systems doing math than about systems doing science/tech/philosophy, and because if my claim is true for math, it'd be profoundly weird for it to be false for any of these other fields.^[52] So, could there be such a well-understood system doing math?
There is the following fundamental issue: to get very far (in a reasonable amount of time/compute), the system will need to effectively be finding/discovering/inventing better ways to think, but if it does that, us understanding the given base structure does not get us anywhere close to understanding the system with all its built structure. The system will only do impressive things (reasonably quickly) if it can make use of radical novelty, if it can think in genuinely new ways, if it can essentially thoroughly reorganize $\approx$ any aspect of its thinking. If you genuinely manage to force a system to only think using/with certain "ideas/structures", it will be crippled.
1. A response: "sure, the system will have to come up with, like, radically new mathematical objects, but maybe the system could keep thinking about the objects the same way forever?". My response to this response: there will probably need to be many kinds of structure-finding; rich structure will need participate in these radically new good mathematical objects being found; you will want to think in terms of the objects, not merely about them (well, to really think remotely well about them, you will need to think in terms of them, anyway)^[53]; to the extent that you can make a system that supposedly "only invents new objects" work, it will already be open to thinking radically differently just using this one route you gave it for thinking differently; like, any thing of this kind that stands a chance will be largely "made of" the "objects" it is inventing and so not understandable solely by knowing a specification of some fixed base apparatus^[54].^[55] I guess a core intuition/(hypo)thesis here is that it’d be profoundly “unnatural”/“bizarre” for thinking not to be a rich, developing, technological sort of thing, just like doing more broadly. Like, there are many technologies which make up a technological system that can support various doings, and there are similarly many thinking-technologies which make up a thinking-technological system which is good for various thinkings; furthermore, the development of (thinking-)technologies is itself again a rich technological thing — really, it should be the same (kind of) thing as the system for supposedly object-level thought.
2. In particular, if you try to identify science-relevant structures in human thinking and make a system out of some explicit versions of those, you either get a system open-endedly searching for better structures (for which understanding the initial backbone does not bestow you with an understanding of the system), or you get an enfeebled shadow of human thought that doesn’t get anywhere.
This self-reprogramming on many/all levels that is (? $\approx$ )required to make the system work needn't involve being explicitly able to change any important property one has. For instance, humans^[56] are pretty wildly (self-)reprogrammable, even though there are many properties of, say, our neural reward systems which we cannot alter (yet) — but we can, for example, create contexts for ourselves in which different things end up being rewarded by these systems (like, if you enroll at a school, you might be getting more reward for learning; if you take a game seriously or set out to solve some problem, your reward system will be boosting stuff that helps you do well in that game or solve the problem); a second example: while we would probably want to keep our thinking close to our natural language for a long time, we can build wild ways to think about mathematical questions (or reorganize our thinking about some mathematical questions) while staying "inside/[adjacent to]" natural language; a third example: while you'd probably struggle to visualize 4-dimensional scenes^[57], you might still be able to figure out what shape gets made if you hang a 4-dimensional hypercube from one vertex and intersect it with a "horizontal" hyperplane through its center.^[58]
Are these arguments strong enough that we should think that this kind of thing is not ever going to be remotely competitive? I think that's plausible. Should it make us think that there is no set of ideas which would get us some such crisp system which proves Fermat's last theorem with no more compute than fits in this galaxy (without us handing it the proof)? Idk, maybe — very universally quantified statements are scary to assert (well, because they are unlikely to be true). But minimally, it is very difficult.

Anyway, if I were forced to give an eleven-word answer to “how does thinking work?”,^[59] I’d say “one finds good components for thinking, and puts them to use”^[60].

But this finding of good components and putting them to use is not some definite finite thing; it is still an infinitely rich thing; there is a real infinitude of structure to employ to do this well. A human is doing this much better than a Jupiter-sized computer doing some naive program search, say.
I'm dissatisfied with “one finds good components for thinking, and puts them to use” potentially giving the false impression that [what I'm pointing to must involve being conscious of the fact that one is looking for components or putting them to use], which is really a very rare feature among instances in the class I have in mind. Such explicit self-awareness is rare even among instances of finding good components for thinking which involve a lot of thought; here are some examples of thinking about how to think:
1. a mathematician coming up with a good mathematical concept;
2. seeing a need to talk about something and coining a word for it;
3. a philosopher trying to clarify/re-engineer a concept, eg by seeing which more precise definition could accord with the concept having some desired "inferential role";^[61]
4. noticing and resolving tensions in one’s views;
5. discovering/inventing/developing the scientific method; inventing/developing p-values; improving peer review;
6. discussing what kinds of evidence could help with some particular scientific question;
7. inventing writing; inventing textbooks;
8. the varied thought that is upstream of a professional poker player thinking the way they do when playing poker;
9. asking oneself "was that a reasonable inference?", “what auxiliary construction would help with this mathematical problem?”, "which techniques could work here?", "what is the main idea of this proof?", "is this a good way to model the situation?", "can I explain that clearly?", "what caused me to be confused about that?", "why did I spend so long pursuing this bad idea?", "how could I have figured that out faster?", “which question are we asking, more precisely?”, "why are we interested in this question?", “what is this analogous to?”, "what should I read to understand this better?", "who would have good thoughts on this?"^[62].
I prefer “one finds good components for thinking, and puts them to use” over other common ways to say something similar that I can think of — here are some: "(recursive )self-improvement”, “self re-programming”, “learning”, and maybe even "creativity" and "originality". I do also like “one thinks about how to think, and then thinks that way”.

Even though intelligence isn't that much of a natural kind,^[63] I think it makes a lot of sense for us to pay a great deal of attention to an artificial system which is smarter than humans/humanity being created. In that sense, there is a highly natural threshold of general intelligence which we should indeed be concerned about. I'll say more about this in Note 8. (Having said that thinking can only be infinitesimally understood and isn't even that much of a definite thing, let me talk about it for 20 more notes :).)

5 confusion isn't going away

There's probably no broad tendency toward the elimination of confused thinking, despite us becoming less confused about any particular "finite question"; this has to do with our interests growing with our understanding/deconfusion.^[64](or family of questions). We could call it "the convergence question" or "the compactness question".

This really depends on the way we're measuring confusion (or its elimination), and different criteria could make sense for different purposes and give genuinely different verdicts, so I've been somewhat provocative here.^[65]

But I think this is probably true when we measure confusion around questions we're interested in (with the caveat that there can still be multiple sensible choices giving different answers here depending on what we're more precisely interested in, so I'm still being slightly provocative).

One consideration here is that we're drawn to places where we're still confused, because that's where there are things to be worked out better. There's a messy confused frontier where we will hopefully be operating indefinitely (or at least until we're around, and if/when we aren't around anymore, other minds will be operating indefinitely at this frontier (until minds are around)).

Another consideration is that mathematics and (relatedly, not independently) technological development provide an infinite supply of interesting things for us to be confused about.

One more (related) consideration is that when we're trying to (eg) prove some theorem or to build some technology, we're likely to still be confused about stuff around it and about how to think well around it, because otherwise we'd already be done with it.

One could try to work on a project of reorganizing thought which aims to push all confusion/ambiguity into probabilities on some hypothetical clear language, but such a project can't succeed in its aim,^[66] because there are probably many interestingly different ways in which it is useful to be able to be confused.^[67]^[68]^[69] You could probably pull off making an advanced mind with a clear structure where only a particular kind of confusion seems to be explicitly allowed, but to the extent that such a mind gets very far, I expect it will just be embedding other ways to think confusedly inside the technically-clear structure you technically-[forced it to have].

All this isn't to say that we shouldn't be trying to become less confused about particular things. I think becoming less confused about particular things (richly conceived) is a central human project (and it is probably a central endeavor for ~all minds)!

More generally, I doubt thinking is or is going to become very neatly structured — I think it'll probably always be a mess, like organic things in general.

To consider an example somewhat distinct from confused thinking: will there be a point in time after which thinking-systems are (or the one big world-thinking-system is) partitioned into distinct thinking-components, each playing some clear role, fitting into some neat structure? I doubt there will be such an era (much like I doubt there will be such an era for the technological world more broadly), for one because it seems good to allow components to relate to other components in varied and unforeseen ways^[70] (in particular, it is good to be able to make analogies to old things to understand new things; if we look at making an analogy from the outside, it is a lot like putting some old understanding-machinery to a new use).^[71] So, thinking-structures will probably (continue to) relate to other thinking-structures in a multitude of ways, with each component playing many roles, and probably with the other components setting the context for each component, as opposed to there being some separate structure above all the components.
That said, certainly there will also be many clean constellations of components in use (like current computer operating systems). Moreover, there are plausibly significant forces/reasons pushing toward thought being more cleanly organized — for instance: (1) cleaner organization could make thought easier to understand, improve, redeploy, control; (2) if some evolution-made thinking-structures in brains get replaced by ones which are more intelligently designed at some point, those would plausibly be made "in the image of some cleaner idea(s)" (compared to evolution's design, and at least in some aspects). It seems plausible that these forces would win [in some "places"]/[for/over some aspects of thought]. I'd like to be able to provide a better analysis of what the forces toward messiness and the forces toward order/structure add up to in various places — I don't think I'm doing justice to the matter here. In particular, I'd like to have a catalogue of comparisons between evolution-made and human-made things meeting some specifications.^[72] I'd love to even just have a better catalogue of the [forces toward]/[reasons for] messiness and the [forces toward]/[reasons for] order/structure (not just in the context of thinking).
Generally, I'd expect eliminating messy thinking-systems to be crippling, and eliminating clean systems to also be crippling. (I'd also expect eliminating confused thinking to be crippling, and eliminating rigorous/mathematico-logical speaking to be crippling.)

6 thinking (ever better) will continue

Could history naturally consist of a period of thinking, of figuring stuff out — for example, of a careful long reflection lasting

10^{5}

years, during which e.g. ethics largely "gets solved" — followed by a period of doing/implementing/enjoying stuff — maybe of tiling the universe with certain kinds of structures, or of luxury consumerism?

Could history naturally consist of a period of fooming — that is, becoming smarter, self-reprogramming, finding and employing new thought-structures — followed by a period of doing/implementing/enjoying stuff — maybe of tiling the universe with certain kinds of structures, or of luxury consumerism?

a mostly-aside: These two conceptions of history are arguably sorta the same, because figuring a lot of stuff out (decently quickly) requires a lot of self-reprogramming, and doing a lot of self-reprogramming (decently quickly) requires figuring a lot of stuff out. And really, one probably should think of gaining new understanding and self-reprogramming-to-think-better as the same thing to a decent approximation. I've included these as separate conceptions of history, because it's not immediately obvious that the two are the same, and in particular because one often conceives of a long reflection as somehow not involving very much self-reprogramming, and also because the point I want to make about these conceptions can stand without having to first establish that these are the same.

It'd be profoundly weird for history to look like either of these, for (at least) the following reasons:

There's probably no end to thinking/fooming.^[73] There will probably always be major interesting problems to be solved, including practical problems — for one, because "how should one think?" is an infinite problem, as is building useful technologies more generally. Math certainly doesn't seem to be on a trajectory toward running out of interesting problems. There is no end to fooming, because one can always think much better.
The doing/implementing/enjoying is probably largely not outside and after the thinking/fooming; these are probably largely the same thing. Thinking/fooming are kinds of doing, and most of what most advanced minds are up to and enjoy is thinking/fooming. In particular, one cares about furthering various intellectual projects, about becoming more skilled in various ways, which are largely fooming/working/thinking-type activities, not just enjoyment/tiling/enjoying-type activites.

This is not to say that it'd be impossible for thinking or fooming to stop. For instance, an asteroid could maybe kill all humans or even all vertebrates, and there could be too little time left before Earth becomes inhospitable [for serious thought to emerge again on Earth after that]. Or we could maybe imagine a gray goo scenario, with stupid self-replicating nanobots eating Earth and going on to eat many more planets in the galaxy.^[74] So, my claim is not that thinking and fooming will necessarily last forever, but that the natural trajectory of a mind does not consist of an era of thinking/fooming followed by some sort of thoughtless era of doing/implementing/enjoying.

So, superintelligence is not some definite thing. If I had to compare the extent to which superintelligence is some definite thing to the extent to which general intelligence is some definite thing, I think I'd say that superintelligence is even less of a definite thing than general intelligence. There's probably not going to be a time after superintelligence develops, like, such that intelligence has now stopped developing. Similarly/equivalently, there's no such thing as a remotely-finished-product-[math ASI].

All this said, it seems plausible that there'd be a burst of growth followed by a long era of slower growth (and maybe eventually decline) on measures like negentropy/energy use or the number of computational operations (per unit of time)^[75] (though note also that the universe has turned out to be larger than one might have thought many times in the past and will plausibly turn out to be a lot larger again). It doesn't seem far-fetched that something a bit like this would also happen for intelligence, I guess.

I should try to think through some sort of more careful economics-style analysis of the future of thinking, fooming, doing, implementing, enjoying. Like, forgetting for this sentence that these are not straightforwardly distinct things, if we were to force a fixed ratio of thinking/fooming to doing/implementing/enjoying, what should we expect the marginal "costs"/"benefits" to look like, and a shift in what direction away from the fixed ratio (and how big a shift) would that suggest?
That said, even if this type of economic argument were to turn out to support thinking/fooming eventually slowing down relative to implementing/enjoying, I might still think that the right intuition to have is that there’s this infinite potential for thinking better anyway, but idk. And I'd still probably think we're probably not anywhere close (in "subjective time") to the end of thought/fooming.^[76]

7 alignment is infinite

What is "the alignment problem"?

We could say that "the big alignment problem" is to make it so things go well around thinking better forever, maybe by devising a good protocol for adopting new [ways of thinking]/[thinking-structures]. I think this big alignment problem is probably in the "complexity class" of infinite problems described in thesis 1; so, we should perhaps say the "alignment endeavor" instead.
There are also various "small alignment problems" — for instance, (1) there is the problem of creating a system smarter than humanity which is fine to create, and (2) there is the problem of ending the current period of (imo) unusually high risk of $\approx$ everything worthwhile being lost forever because of AI.^[77] Problem (1) is quite solvable, because humanity-next-year will be such a system,^[78] or because humans genetically modified to be somewhat smarter than the smartest humans currently alive would probably be fine to create, or because there is probably a kind of mind upload which is fine to create in some context which we could set up (with effort).^[79] Problem (2) is also quite solvable, because conditional on it indeed being a very bad idea to make a smarter-than-human and non-human artifact, it is possible to get humanity to understand that it is a very bad idea and act responsibly given that understanding (ban AGI) and severely reduce the annual risk of everything meaningful being wiped out.

Why is the big alignment problem infinite?

It seems likely that one ought to be careful about [becoming smarter]/[new thinking/doing-structures coming into play] forever, and that this being careful just isn't the sort of thing for which a satisfactory protocol can be specified beforehand, but the sort of thing where indefinitely many arbitrarily different new challenges will need to be met as they come up, preferably with the full force of one's understanding at each future time (as opposed to being met with some fixed protocol that could be specified at some finite time). There is an infinitely rich variety of new ways of thinking that one should be open to adopting, and it'd be bizarre if decisions about this rich variety of things could be appropriately handled by any largely fixed protocol.
to say more: There's no hope to well-analyze anything but an infinitesimal fraction of the genuinely infinite space of potential [thinking/doing]-structures, and it is hard to tell what needs to be worked out ahead of time. Well-handling a particular [thinking/doing]-structure often requires actually thinking about it in particular to a significant extent (though one can of course bring to bear a system of understanding built for handling previous things, also), and there's a tension in being able to do that significantly before the thinking-structure comes on the scene, because (1) if the structure can be seen clearly enough to be well-analyzed or even identified as worthy of attention, then it is often in use already in use or at least close to coming into use and (2) understanding it acceptably well often sorta requires playing around with it, so it must plausibly already be used (though maybe only "in a laboratory setting") for it to be adequately understood. Like, it's hard to imagine a bright person in 1900 identifying the internet as a force which should be understood and managed and going on to understand it adequately; it's hard to imagine someone before Euclid (or before whenever the axiomatic method in mathematics as actually developed) developing a body of understanding decent for understanding the axiomatic method in mathematics (except by developing the axiomatic method in mathematics oneself) (and many important things about it were in fact only understood two millennia later by Gödel and company); it's hard to imagine humans without language being well-prepared for the advent of language ahead of time (this is an example where the challenge is particularly severe). So, we should expect that in many cases, the capacity to adequately handle a novel [thinking/doing]-structure would only be developed only after it comes on the scene or as it is coming on the scene or only a bit before it comes on the scene.
A potential response: "Okay, let's say I agree that there is this infinitely rich space of thinking-structures, and that one really just needs to keep thinking to handle this infinitely rich domain. But couldn't there be a finite Grand Method for doing this thinking?". My brief response is that this thinking will need to be rich and developing to be up to the challenge (as long as one is to continue to develop). It seems pretty clear that this question is roughly equivalent to "couldn't there be a Protocol for math/science?""; so, see Notes 1–6 for a longer response to this question. (And if you try to go meta more times, I'll just keep giving the same response. It's not like the higher meta-levels are any easier; actually, it's not even like we'd want them to be handled by some very distinct thinking.)
This isn't to say that handling alignment well looks like handling an infinite variety of completely unique particulars (just like that's not what (doing) math looks like). One still totally can and totally should be developing methods/tools/ideas/understanding with broad applicability (just like one does in math) — it's just that this is an infinite endeavor. For example, I think it's a very good broadly applicable "idea" to become smarter oneself instead of trying to create some sort of benevolent alien entity. A further very good broadly applicable "idea" is to be extremely careful/thoughtful about becoming smarter as you are becoming smarter.

Even though it's sort of confused to conceive of "the alignment problem" as a finite thing that could be solved, confused to imagine a textbook from the future solving alignment, it is totally sensible and very good for there to be a philosophico-scientifico-mathematical field that studies the infinitely rich variety of questions around how one^[80] should become smarter (without killing/losing oneself too much). We could call that field "alignment".^[81] (It might make sense for alignment to be a topic of interest for people in many fields, not a very separate field in its own right; it should probably be done by researchers that think also more broadly about how thinking works, and about many other philosophical and mathematical matters.)

But again, for each particular time, the problem of making an intelligent system which is smarter than we are currently and which is fine to make is totally a finite problem, e.g. because it is fine to become smarter by doing/learning more math/science/philosophy. Also, one might even get to a position where one could reasonably think that things will probably be good over a very long stretch of gaining capabilities (I'm currently very uncertain here^[82]). But even if this is possible, (I claim) this cannot be achieved by writing a textbook ahead of time for how to become smarter and just following that textbook (or having the protocol specified in this textbook in place) over a long stretch of time — as one proceeds, one will need to keep filling the shelves of an infinite alignment library with further textbooks one is writing.
Let me speedrun some other interesting questions about which textbooks could be written. Of course, the questions really deserve much more careful treatment. In my answers in this speedrun (in particular, in the specification gaming I will engage in), I will be guided by some background views which I have not yet properly laid out or justified in this initial segment of the notes — specifically, including and surrounding the view that it is a tremendously bad idea to make an artifact which is more intelligent than us and distinct/separate from us any time soon (and maybe ever). But laying out and justifying these views better is a central aim of the remainder of these notes.
1. "Is there some possible 100000-word text which would get us out of the present period of (imo) acute x-risk from artificial intelligence?" I think there probably is such a book, because if I'm indeed right that we are currently living through a period of acute risk, there could be a 100000-word text making a case for this which is compelling enough that it gets humanity to proceed with much more care; alternatively, one could specify a way to make humanity sufficiently smarter/wiser that we realize we are living through a period of acute risk ourselves (again, assuming this is indeed so); alternatively, one could give the most careful humans a "recipe" for mind uploads and instructions for how to set up a context in which uploading all humans meaningfully decreases x-risk (per unit of subjective time, anyway); etc — there is probably a great variety of 100000-word texts that would do this. Any such text has a probability of at least ${(10^{5})}^{- 100000}$ to be "written" by a (quantum) random number generator, so for any such text, there is at least this astronomically small probability we would "write it" ourselves (lol); but really, I think it is realistically possible (idk, like, $p > 10^{- 4}$ if we try?) for us to write any of the example texts from the previous sentence ourselves.
2. "But is there a text which lets us make an AI which brings our current era of high x-risk to a close?" Sorta yes, e.g. because mind uploads are possible and knowing how to make mind uploads could get us to a world where most people are uploaded and become somewhat better at thinking and understand that allowing careless fooming is a bad idea (assuming it indeed is a bad idea) and such a world would plausibly have lower p-doom per subjective year (especially if the textbook also provides various governance ideas) :).
3. "But is there one which lets us make a much more alien mind which is smarter than us which is good to make?" Sorta yes, e.g. because we could still have the alien mind output a different book and self-destruct :).
4. "Argh, but is there a text which lets us make a more alien mind which is smarter than us and good to make which then directly does big things in the world (+ additional conditions to prevent further specification gaming) which is good to make?" I think there probably is a text which would give the source code of a mind which is already somewhat smarter than us, which is only becoming smarter in very restricted ways, and which does nothing except destroying any AGIs that get built, withstanding human attempts to disable it for a century (without otherwise doing anything bad to humans) and then self-destructing.^[83]
5. "But is there a text which looks like a textbook (so, not like unintelligible source code) which lets us understand relevant things well enough that we can build an alien AI that does the thing you stated in the previous response?"^[84] Now that the textbook cannot directly provide advanced understanding that the AI could use and it probably needs to become really smart from scratch and we cannot be handed a bespoke edit to make to the AI which makes it "sacrifice itself" for us this way, it seems much tougher, but I guess it's probably possible, even though I lack any significantly "constructive" argument. I'm very unsure/confused about whether there will ever be a time in future history when we could reasonably write this kind of text ourselves (such that it is adequate for our situation then). I think it's plausible that there will be no future point at which we should try to execute a plan of this kind that we devised ourselves (over continuing to do something that looks much more like becoming smarter ourselves^[85]).
6. "What if the AI we can make given the textbook is supposed to act as a guardian of humanity over a very long stretch of [it and humanity] becoming smarter, with it staying ahead of humanity indefinitely? Or maybe there could be some other futures in which this AI is the smartest thing around indefinitely that are still somehow good?"^[86] The median difficulty of this is significantly higher still. The question makes me want to return to specification gaming (eg, what if the AI "becomes a human" after a while? does it count if it basically has the values and understanding of a human but after some careful fooming so it is alien in a sense?). I sorta feel like not answering this particular question here (partly because I don't understand this matter well at present), but I will say the following: (1) this is minimally incredibly difficult and we should not be making an AI which would indefinitely be smarter than humanity any time soon; (2) I will provide (further) arguments for (1) in later notes in this sequence; (3) I think it is likely that this will never be a good idea (and we should just continue to become smarter ourselves); (4) these questions about the possibility of such a thing will also be addressed in later notes in this sequence, though somewhat obliquely; and (the primary point of the present note is/implies that) (5) work on how one ought to become smarter (alignment) would need to be continued by such an AI indefinitely.

And, to be clear, nowhere here am I talking particularly of [provably having a good future around gains in intelligence] being an infinite problem which requires indefinite work — instead, I am saying that if we are to handle gains in intelligence even remotely well, we must be thinking our way through genuinely new challenges indefinitely — there is not some finite grand protocol to be found to adequately handle gains in capability. One's body of understanding for handling becoming smarter will need to be rich, developing (if it is to remain even remotely up to the task), and forever mostly incomplete.

Even conditioning on alignment being a finite problem to be “solved”, I think it could only be solved as one of the very last problems to be solved ever — like, it gets solved around when math and technology get “solved”, not earlier. What's more, at that point (once math and technology have been solved), there'd probably no longer be any need to solve the alignment problem anyway, because there probably wouldn't be anything left which one would want this further intelligent system to do for one.

In case you happen to be hopeful about any plans for navigating super-human AI involving getting AIs to "solve alignment" (in the sense of solving it for good) for us, it might be worth revisiting those hopes after pondering the above points.^[87]

To what extent does alignment being infinite (for our purposes) depend on some particular property of our values? Does my claim that alignment is infinite (for our purposes) rest on some implicit claim about our values?

First, to clarify, the central claim of this note is that for pretty much any values, if one is to become arbitrarily better at thinking, one should(-according-to-one's-own-values) really keep thinking about how one should become better at thinking, with this thinking being always-mostly-unfinished and developing.
But, separately from the above conditional claim, maybe there are some values such that one shouldn't(-according-to-those-values) become arbitrarily better at thinking? And if you aren't looking to become arbitrarily capable, maybe alignment needn't be an infinite endeavor for you? Given this, isn't the infinitude-for-us of alignment dependent on some fact about our values?
1. Sure, some intelligent being probably could have values such that they would e.g. be happy to make fairly dumb probes which (absent intelligent intervention) turn most planets in our galaxy into diamond or something, and then make and launch those and eliminate all intelligent entities able to stop the probes (including themselves). We could maybe kinda-sorta imagine a group of human terrorists doing this at some point in some futures. For such an entity, alignment needn't be an infinite endeavor — such a hypothetical entity could be fine with stopping thinking about how to become smarter once it has finished doing its finite thing.
2. But I think such values are really "strange/unlikely" — I think that almost any values ask one to continue becoming more intelligent/capable at any stage of development (though temperance in one's fooming might well be commonly considered right). Minimally, this is to solve various problems one faces and to make progress on one's various projects more generally; it is probably also common to have many profound projects which are just fairly directly about becoming smarter (just like humanity already to some extent "terminally cares" about various philosophical/mathematical/scientific/technological projects). In particular, our own values are probably (going to continue being) like this.
3. So, I think our values will continue asking us to become more capable, and that this isn't really because of some empirical contingency — it is not the case that we could well have ended up with values that are not like this. However, I do think this is downstream of some "logical facts" about values that one could well be wrong/confused about. These themes will receive further treatment in upcoming notes in this sequence.

This isn't to say that you should be unambitious when trying (to do research) to make things go well around intelligence/capability gains. I'm asking you not to be a certain kind of (imo) crazy/silly, but conditional on not being that kind of crazy/silly, please be very ambitious. Most alignment/safety researchers would do well to work on much more ambitious projects.

In particular, alignment being infinite and any progress on alignment being an infinitesimal fraction of all possible progress does not imply that anything is as good as anything else — there are still totally things which are more substantive/important/useful and things which are less substantive/important/useful, just like in math. And even more strongly, alignment being infinite does not imply that whatever research you're doing is good.^[88]

8 making an AI which is broadly smarter than humanity would be most significant

The previous notes might leave the impression that I think the future of thinking looks like business as usual. The point of this note is to clarify some ways in which I very much do not think this.

Yes, I think it is unlikely that "the history/development of thought will end"^[89], but I very much don't think that the future just brings more of the usual.

First, what I've been saying is "in many ways, the future will be like it has been before — that is, it brings completely crazy things which cannot be remotely-well-anticipated, like arithmetic, the printing press, probability, formal logic, computers, or maybe even like primitive compositional language^[90], very many times", which is hardly well-captured by "the future just brings more of the usual" alone.

Second, these notes are written during a period with a high probability per year of humanity making an artificial system more intelligent/capable than us^[91]. That would very much not be "business as usual" — I think it would plausibly be comparably important to evolution or culture getting started, given the central role that intelligence/capability has in the world and the fact that gains in intelligence and understanding will likely be much faster (by default) [once an artifact smarter than humans/humanity has been created] than they have been historically in humanity/humans.

One reason things will be crazy once such an artifact is created is that it makes thinking much more open to being intelligently reshaped than before (including just scaling a mind up). A great deal of somewhat intelligent design of thinking has happened already (for example, humanity is doing some of that (roughly) every time we create a new useful word-concept), but making an artifact more intelligent than us and distinct from us will almost certainly make much more powerful forms of reshaping thought available — it would open up many aspects of thought to much more potent kinds of improvement.
For a very weak lower bound on what happens by default, imagine just being able to make very many "people" at least as smart as the smartest people who have appeared so far, and running them $100$ times faster, potentially making as much scientific/mathematical/philosophical progress in a year as might have taken a century without artificial intelligence. In particular, you can have this much progress be made in the field of artificial intelligence itself. Really, things will be much crazier than 100 years of usual progress happening in 1 year.
Generally, intelligence is just very powerful! Like, the structures in our world are almost entirely made by thought-like processes. When you look around, almost all the objects you see had to be invented by people or by evolution (or the two together) — if you look right, you see "reified/implemented ideas" everywhere — and there is very very much more significant stuff to invent.^[92] The world is only going to become much more shaped/built by thinking than it is now (assuming thinking sticks around). Your own mind is made using evolution's "thinking" and humanity's thinking and in particular your own thinking and your parents’/teachers’/friends’ thinking.

Furthermore, by default, the intelligent system(s) we'd create would be radically different from us — this contributes further to the creation of such a system being a drastic event.

So, given that by default, an artifact more intelligent/capable than us is created this century, by default, it is "the big thing" of our time.

In particular, I might improve/rewrite/expand and republish some of the present notes in the future. ↩︎
though I expect a bunch of them to eventually come to be of type nonsense ↩︎
You know how when people in the room are saying $X$ and you think sorta- $X$ -but-sorta-not- $X$ , then you might find yourself arguing for not- $X$ in this room (but if you were trying to be helpful in a room of not- $X$ -ers, you'd find yourself arguing for $X$ in that room), and it's easy to end up exaggerating your view somewehat in the direction of not- $X$ in this situation? These notes have an early archeological layer in which I was doing more of that, but I decided later that this was annoying/bad, so this early layer has now largely been covered up in the present palimpsest. The title (hypo)theses are a main exception — to keep them crisp, I've kept many of them hyperbolic (but stated my actual position in the body of the note). ↩︎
especially given that to a significant extent, the claims stand together or fall together ↩︎
if in a few years I don’t think I was wrong/confused about major things here, I should seriously consider considering myself to have died :) ↩︎
Still, it could happen that I don't respond to a response; in particular, it could happen that [I won't find your attempt to reason me out of some position compelling, but I also don't provide counterarguments], and it could happen that I learn something from your comment but fail to thank you. So, you know, sorry/thanks ahead of time :). ↩︎
I use scare quotes throughout these notes to indicate terms/concepts which I consider particularly bad/confused/unreliable/suspect/uncomfortable/unfortunate/in-need-of-a-rework; I do not mean to further indicate sneering. (I also use double quotation marks in the more common way though — i.e., just to denote phrases.) ↩︎
or multiple artifacts distinct and separate from us which outgrow us ↩︎
I might go through the notes at some point later and add more specific acknowledgments — there are currently a bunch of things which are either fairly directly from someone or in response to someone or developed together with someone. Many things in these notes are really responses to past me(s), though I don't take them to exactly have taken a contrary (so wrong :)) position most of the time, but more [to have lacked a clear view on] or [to have had only bad ways to think about] matters. ↩︎
in isolation, this note would have been titled "the notion of an infinite endeavor", but that wouldn't have accorded with the schema of each note being a (hypo)thesis ↩︎
we could alternatively say: to which there are finite satisfactory answers ↩︎
some examples of finite problems: finding a proof or disproof of a typical conjecture in math, coming up with and implementing a data structure where certain operations have some particular attainable complexities, building a particular kind of house, coming up with special relativity (or, more generally, coming up with anything which people have already come up with); identifying the fundamental laws of physics is probably finite (but I also have some reasonable probability on it being infinite or not making sense or maybe splitting into a multitude of finite and infinite problems, e.g. involving some weirdness around finding yourself inside physics or something or around being able to choose one's effective laws — idk) ↩︎
some other infinite problems: physics, writing novels, hip-hop, cooking mushroom pies, completing the system of german idealism, being funny ↩︎
If you don't feel like this about math now, I'd maybe ask you to also consider math in 1900, or, if there's some other field of inquiry you're quite familiar with, to consider that field. (To be clear: this isn't to say that after you do this, I think you should definitely be agreeing with me here — I'm open to us still having a disagreement after, and I'm open to being wrong here, or to needing to clarify the measure :).) I'll note preemptively that many sciences are sort of weird here; let me provide some brief thoughts on whether physics is infinite as an example. One central project in current physics is to figure out what the fundamental laws of physics are; this project could well be finite. However, I think physics is probably infinite anyway. A major reason is that physics is engaged in inventing/manufacturing new things/phenomena/situations/arenas and in studying and making use of these (and other) more "invented/created" things; some examples: electric circuits, (nuclear (fusion)) power plants, (rocket) engines, colliders, lenses, lasers, various materials, (quantum) computers, simulations. (Quite generally, the things we're interested in are going to be "less naturally occurring (in the physical universe)" over time.) Also, even beyond these activities, [a physicist's ways of thinking]/[the growing body of ideas/methods/understanding of physics] would probably continue to be significant all over the place (for example, in math). ↩︎
I would probably also not want to consider this a remotely satisfactory algorithm, but this is a much smaller objection. ↩︎
as opposed to being asked in some sense such that a specification of the fundamental laws of physics would be an adequate answer ↩︎
https://youtu.be/_W18Vai8M2w?t=163 ↩︎
The weaker claim that I could make here is that this is only true typically — i.e., that "if $P$ is infinite, then "how should one do $P$ ?" is usually also infinite. I think the weaker claim would be fine to support the rest of the discussion, but I've decided to go with the stronger claim for now as it still seems plausible. To adapt an ancient biology olympiad adage: it might be that all universally quantified statements are false, but the ones that are nearly true are worth their weight in gold. Anyway, I admit that the claim being true ends up depending on how one measures progress on a problem (as discussed briefly also in the last item), which I haven't properly specified. For these notes, I would like to keep getting away with saying we're measuring progress in some intuitive way which is like the way mathematicians measure progress when saying math is infinite. ↩︎
I think the metaethical problem of providing sth like axioms for ethics is also infinite, despite the fact that it could be reasonable to consider the analogous problem for math finite given that we can develop (almost) all our math inside [first-order logic]+ZFC. One relevant difference between this metamathematical problem and this metaethical problem is that any system which supports sufficiently rich structure can be a fine solution to the metamathematical problem because we can then probably make $\approx$ all our mathematical objects sit inside that system, whereas it is far from being the case that anything goes to this extent for the metaethical problem — it being fine to use the hypothetical ethical system to guide action feels like a much stricter requirement on it, and in fact probably entangles the choice with ethics sufficiently to make this problem infinite, also. Additionally, it being imo plausibly infinite to make some decision on what the character of value is also pushes this metaethical problem toward infinitude. What's more, such a formal system would not only need to "contain" our values, but also our understanding (I will talk more about this in a later note), but our understanding is probably not something on which any fixing decision should ever be made because we should remain open to thinking in new ways, so any hypothetical such system would be going out of date after it is created (at least in its "understanding-component", but I also doubt a principled cleavage can be made (I'll discuss various reasons in upcoming notes)). Also, our understanding and values at any time $t$ are also probably much too big for us to see properly at that time $t$ , as well as not in a format to fit in any canonically-shaped such system. That said, there is a "small problem of providing an ethical system" which just asks for any kind of "system" which is sorta fine to give control to according to one's values (relative to some default), which is solvable because e.g. humanity-tomorrow will be such a system for humanity. ↩︎
By $E$ reducing to $F$ , I roughly mean the usual thing from computer science: that there is a cheap/easy way to get a solution to $E$ from a solution to $F$ ; this implies that if you could solve $F$ , you could also solve $E$ . If we conceive of each endeavor as consisting of collecting/solving some kinds of pieces, then we could also require a piece-wise map here: that for each piece of $E$ , one can cheaply specify a piece of $F$ such that having solved/collected that piece of $F$ would make it cheap for one to solve/collect that piece of $E$ as well. I'm adding the further condition that the reduction be "faithful" to rule out cases where a full solution to $F$ would give you a solution to $E$ , but one can nevertheless get a positive fraction of the way in $F$ without doing anything remotely as challenging as $E$ — for example, take $F$ to be the disjoint union of playing a game of tic-tac-toe and math, with equal total importance assigned to each, and take $E$ to be math. I'm not sure what I should mean by a reduction being "faithful" (a central criterion on its meaning is just to make the statement about transferring infinitude true), but here are a few alternatives: (1) If we can think of $E$ and $F$ in terms of collecting pieces with importance-measures in $R^{\geq 0}$ , then it would be sufficient to require that the reduction map doesn't distort the measures outrageously. (2) We could say that any $[\geq \frac{1}{3}]$ -solution of $F$ would cheaply yield a $[\geq c]$ -solution (with $c > 0$ ) of $E$ , or that any way to remotely-well-solve $F$ would cheaply give rise to a way to remotely-well-solve $E$ , but this is plausibly too strong a requirement. (3) We could say that if there were a $[\geq \frac{1}{3}]$ -solution of $F$ , there would be another solution of $F$ which isn't "infinitely many times more challenging (to find)" which would cheaply yield a $[\geq c]$ -solution (with $c > 0$ ) of $E$ . In other words, we'd say that there is a reasonably economical way to go about $[\geq \frac{1}{3}]$ -solving $F$ which would involve $[\geq c]$ -solving $E$ as well. Actually, for most infinitude-transfers one might want to handle with this rule, I think it might also be fine to do without a "precise" statement, just appealing to how $F$ is intuitively at least as challenging as $E$ . ↩︎
Any non-infinitesimal fraction should definitely count as a "decently big part"; the reason I didn't just say "positive fraction" to begin with is that I'd maybe like this principle to also helpfully explain why some sufficiently big infinitesimal fractions of infinite problems are infinite. ↩︎
a footnote analogous to the first footnote about the first item on this sublist ↩︎
Is the infinitude of "how should one think?" the "main reason" why philosophy is infinite? Is it the main reason for most particular infinite philosophical problems being infinite? I would guess that it is not — that there are also other important reasons; in particular, if a philosophical problem is infinite, I would expect there to at least also be some reason for its infinitude which is "more internal to it". In fact, I suspect that clarifying the [reasons why]/[ways in which] endeavors can end up infinite is itself an infinite endeavor :). ↩︎
In addition to stuff done by people canonically considered philosophers (who have also made a great deal of progress), I’d certainly include as central examples of philosophical progress many of the initial intellectual steps which led to the creation of the following fields: probability and statistics, thermodynamics and statistical mechanics, formal mathematical logic, computability and computer science, game theory, cybernetics, information theory, computational complexity theory, AI, machine learning, and probably many others; often, this involved setting up an arena in which one could find clear/mathematical counterparts to some family of previously vague questions. (I’d also consider many later intellectual steps in these fields to be philosophical progress.) ↩︎
Doing some amount of the inside thing is hard to avoid because we can't access ourselves except from the inside, and even if we had some other access channel, we'd struggle to operate well on an aspect of ourselves except by playing around with it on the inside a bunch — think also about eg how to help someone out of a confusion (about a theorem, say), it can help to try to think in that confused way yourself, and eg how playing a game (or at least seeing it played) is centrally good for improving it. Some amount of the outside thing is also usually unavoidable — we are reflective by default and that's good — think eg about how it is actually good/necessary to also look at a game from the outside to improve it, not to just keep playing it (though a human will of course be doing a great deal of looking at the game even when just playing it), and about why it's good that we are able to talk about propositions and not solely about more thingy things (or, well, about why it's good we can turn propositions into ordinary thingy things). ↩︎
Really, I’m somewhat unhappy with the language I have here — “how should thinking work?” sounds too much like we’re only taking the external position. I would like to have something which makes it clearer that we have here is like a game at once played and improved. ↩︎
The object/meta distinction is sort of weird to maintain here; its weirdness has to do with us being reflective creatures, always thinking together about a domain and about us [thinking about]/[doing stuff in] the domain. When you are engaged in any challenging activity, you're not solely "making very object-level moves", but also thinking about the object-level moves you're making; now, of course, the thinking about object-level moves you're making can also itself naturally be seen as consisting of moves in that challenging activity, blurring the line between object-level-moves and meta-moves. And I'm just saying this is true in particular for challenging thinking-activities; in such activities, the object-moves are already more like thought-moves, and the meta-moves are/constitute/involve thinking about your thinking (though you needn't be very explicitly aware that this is what you're doing, and you often won't be). A mathematician doesn't just "print statements" without looking at the "printing process", but is essentially always simultaneously seeking to improve the "printing process". And this isn't at all unique to mathematics — when a scientist or a philosopher asks a question, they also ask how to go about answering that question, seek to make the question make more sense, etc.. (However, it is probably moderately more common in math than in science for things which first show up in thinking to become objects of study; this adds to the weirdness of drawing a line between object and meta in math. Here's one stack of examples: one can get from the activities of [counting, ordering, measuring (lengths, areas, volumes, times, masses), comparing in quantity/size, adding, taking away, distributing (which one does initially with particular things)] to numbers (as abstract things which can be manipulated) and arithmetic on numbers (like, one can now add 2 and 3, as opposed to only being able to put together a collection of 2 objects of some kind with a collection of 3 objects of another kind), which is a main contributor to e.g. opening up an arena of mathematical activities in elementary number theory, algebra, and geometry; one can get from one doing operations/calculations to/with numbers (like squaring the side length of a square to find its area) to the notion of a function (mapping numbers to numbers), which contributes to it becoming sensible to e.g. add functions, rescale functions, find fourier decompositions of periodic functions, find derivatives, integrate, find extrema, consider and try to solve functional equations; one can again turn aspects of these activities with functions into yet more objects of study, e.g. now getting vector spaces of functions, fourier series/transforms (now as things you might ask questions about, not just do), derivatives and integrals of functions, functionals, extremal points of functions, and differential equations, and looking at one's activities with functions can e.g. let/make one state and prove the fundamental theorem of calculus and the extreme value theorem; etc.. (I think these examples aren't entirely historically accurate — for example, geometric thinking and infinitesimals are neglected in the above story about how calculus was developed — but I think the actual stories would illustrate this point roughly equally well. Also, the actual process is of course not that discrete: there aren't really clear steps of getting objects from activities and starting to perform new activities with these new objects.) (To avoid a potential misunderstanding: even though many things studied in mathematics are first invented/discovered/encountered "in" our (thinking-)activities, I do not mean to say that the mathematical study of these things is then well-seen as the study of some aspects of (thinking-)activities — it's probably better-seen as a study of some concrete abstract things (even though it is often still very useful to continue to understand these abstract things in part by being able to perform and understand something like the activities in which they first showed up).) Philosophy also does a bunch of seeing things in thought and proceeding to talk about them; here's an example stack: "you should do X"-activities -> the notion of an obligation -> developing systems of obligations, discussing when someone has an obligation -> the notion of an ethical system/theory -> comparing ethical theories, discussing how to handle uncertainty over ethical theories -> the notion of a moral parliament. Of course, science also involves a bunch of taking some stuff discovered in previous activities as subject matter — consider how there is a branch of physics concerned with lenses and mirrors and a branch concerned with electric circuits (with batteries, resistors, capacitors, inductors, etc.) or how it's common for a science to be concerned with its methodology (e.g., econometrics isn't just about running regressions on new datasets or whatever, but also centrally about developing better econometric methods) — but I guess that given that this step tends to take one from some very concrete stuff in the world to some somewhat more abstract stuff, there's a tendency for these kinds of steps to exit science and land in math or philosophy (depending on whether the questions/objects are clearly specified or not) (for example, if an econometrician asks a clear methodological question that can be adequately studied without needing to make reference to some real-world context, then that question might be most appropriately studied by a [mathematical statistic]ian).) ↩︎
I should maybe say more here, especially if I actually additionally want to communicate some direct intuition that the two things are equi-infinite. ↩︎
this should maybe be split into more classes (on each side of the analogy between technological things and mathematical things) ↩︎
one can make a further decision about whether to look "inside" the rationals as well here ↩︎
incidentally, if you squint, Gödel's completeness theorem says that anything which can be talked about coherently exists; it'd be cool to go from this to saying that in math, given any "coherent external structure", there is an "internal structure"/thing which [gives rise to]/has that external structure; unfortunately, in general, there might only be such a thing in the same sense that there is a "proof" of the Gödel sentence $G$ — (assuming PA is consistent) there is indeed an object $x$ in some model of PA such that the sentence we thought meant that $x$ is a proof of $G$ evaluates to True, but unfortunately for our story (and fortunately for the coherence of mathematics), this $x$ does not really correspond to a proof of $G$ . ↩︎
One could try to form finer complexity classes (maybe like how there are different infinite cardinalities in set theory), i.e., make it possible to consider one infinite problem more infinite than another. I'd guess that the problems considered here would still remain equi-infinite even if one attempts some reasonable such stratification). ↩︎
I think there are also many other important kinds of thinking-technologies — we're just picking something to focus on here. ↩︎
something like this was used for AlphaGeometry (Fig. 3) ↩︎
For example, you might come up with the notion of a graph minor when trying to characterize planar graphs. The notion of a graph minor can "support" a characterization of planar graphs. ↩︎
I find it somewhat askew to speak of structures "in the brain" here — would we say that first-order logic was a structure "in the brain" before it was made explicit (as opposed to a structure to some extent and messily present in our (mathematical) thought/[reasoning-practices])? But okay, we can probably indeed also take an interest in stuff that's "more in the brain". ↩︎
I don't actually have a reference here, but there are surely papers on plants responding to some signals in a sorta-kinda-bayesian way in some settings? ↩︎
I'd also say the same if asked to guess at a higher structure "behind/in" doing more broadly. ↩︎
Language and words are largely (used) for thinking, not just for transferring information. ↩︎
words and mathematical concepts and theorems are also sorta tools, so I should really say e.g. "we also make more external tools" in this sentence ↩︎
well, all the useful ones, anyway ↩︎
including by hopefully opening up a constellation of questions to further inquiry ↩︎
you know, like $[- 1, 1]^{3}$ ↩︎
If that's too easy for you, I'm sure you can find a tougher question about the cube which is appropriate for you. Maybe this will be fun: take a uniformly random 2-dimensional slice through the center of an $n$ -dimensional hypercube; what kind of 2-dimensional shape do you see, and what's the expected number of faces? (I'm not asking for exact answers, but for a description of what's roughly going on asymptotically in $n$ .) ↩︎
this is particularly true in the context of trying to solve alignment for good; it is plausibly somewhat less severe in the context of trying to end the present period of (imo) acute risk with some AI involvement; I will return to these themes in Note 7 ↩︎
let's pretend quantum mechanics isn't a thing ↩︎
I think there's a unity to being good at things, and I admit that the cluster of views on intelligence in these notes — namely, thinking this highly infinite thing, putting to use structures from a very diverse space — has some trouble/discomfort admitting/predicting/[making sense of] this. While I think there's some interesting/concerning tension here, I'm not going to address it further in these notes. ↩︎
by "fooming", I mean: becoming better at thinking, understanding more, learning, becoming more capable/skillful ↩︎
ignoring the heat death of this universe or some other such thing that might end up holding up and ignoring terrorism (e.g. by negative utilitarians :)) etc., the history of thought will probably always only be getting started ↩︎
in this example, the truth values are the "content" ↩︎
For example, you might just be going through all finite strings in order, checking for each string whether it is a valid proof of some sentence from the axioms, and if it is, assigning truth value $1$ to that sentence and truth value $0$ to its negation. ↩︎
Like, if there were any difference between the areas here, it'd surely involve math being more doable with a crisp system than science/tech/philosophy? ↩︎
it might help to take some mathematical subject you're skilled in and think about how you operate differently in it now that you have reprogrammed yourself into thinking in terms of its notions, comparing that to how you were thinking when solving problems in the textbook back when you were first learning it (it might help to pick something you didn't learn too long ago, though, so you still have some sense of what it was like not to be comfortable with it; alternatively/additionally, you could try to compare to some other subject you're only learning now) — like, if you're comfortable with linear algebra, think about how you can now just think in terms of vectors and linear maps and kernels and singular value decompositions and whatever, but how when you were first learning these things, you might have been translating problems into more basic terms that you were familiar with, or making explicit calls to facts in the textbook without having a sense of what's going on yourself ↩︎
and again, your own thinking is not just “operating on” your concepts, but also made (in part) of your concepts ↩︎
One could try to see this picture in terms of the (constitutive) ideas involved in thinking being “compute multipliers”, with anything that gets very far in not too much compute needing to find many compute multipliers for itself. ↩︎
especially young humans ↩︎
though you might even just be able to train yourself into being able to do that, actually ↩︎
That is, what 3-dimensional body is this intersection? ↩︎
maybe after I've already said "thinking is an organic/living, technological, developing, open-ended, on-all-levels-self-reinventing kind of thing", as I have above ↩︎
I'm aware that this would be circular if conceived of as a definition of thinking. ↩︎
I feel like this might sound spooky, but I really think it isn't spooky — I'm just trying to describe the most ordinary process of reworking a concept. One reason it might sound spooky is that I'm describing it overly from the outside. From the inside, it could eg look like noting that knowledge has some properties, and then trying to make sense of what it could be more precisely given that it has those properties. ↩︎
note also that one can be improving one's thinking in these ways without explicitly asking these questions ↩︎
what I mean by this is more precisely is just what I've said above ↩︎
Here's some context which can hopefully help make some sense of why one might be interested in whether confusion is going away (as well as in various other questions discussed in the present notes). You might have a picture of various imo infinite endeavors in which pursuing such an endeavor looks like moving on a trajectory converging to some point in some space; I think this is a poor picture. For example, this could show up when talking of being in reflective equilibrium or reflectively stable, when imagining coherent extrapolated volition as some sort of finished product (as opposed to there being a process of "extrapolation" genuinely continuing forever), when talking of a basin of attraction in alignment, when thinking of science or math as converging toward some state where everything has been understood, when imagining reaching some self-aware state where you've mostly understood your own thinking (in its unfolding), when imagining reaching some self-aware state where you've mostly understood your own thinking (in its unfolding), or, in the case of this note, when imagining deconfusion/philosophy/thinking as approaching some sort of ultimate deconfused state. If we want to think of a mind being on a trajectory in some space, I'd instead suggest thinking of it as being on a trajectory of flight, running off to infinity in some weird jagged fashion in a space where new dimensions keep getting revealed (no, not even converging in projective space or whatever). Or (I think) better still, we could maybe imagine a "(tentacled?) blob of understanding" expanding into a space of infinitely high dimension (things should probably be discrete — you should probably imagine a lattice instead of continuous space), where a point being further in the interior of the blob in more directions corresponds to a thing being [more firmly]/[less confusedly] understood (perhaps because of having been more firmly put in its proper context) — given reasonable assumptions, it will always remain the case that most points in the blob are close to the boundary of the blob in many directions (a related fact: a unit ball in high dimension has most of its volume near its surface) so "the blob" will always remain mostly confused, even though any particular point will eventually be more and more securely in the interior of the blob so any particular thing will eventually be less confusedly grasped. To be clear: the present footnote is mostly not intended as an argument in support of this view — I'm mostly just stating the question ↩︎
Also, I haven't really decided if I want to be saying something about the importance of confusion relative to other stuff or if I want to be saying something about whether confusion will continue to play a very important role instead. ↩︎
That said, the project could totally succeed in other ways — for example, trying to address some issue with a naive construction of such a language, one could discover/[make explicit]/invent a novel thinking-structure. ↩︎
Incidentally: I’m clearly confusedly failing to distinguish between different kinds of confusion in this note :). ↩︎
For example, it is probably good for many purposes to employ an "ecological arsenal" of concepts — in particular, to have concepts be ready to "evolve", "take on new responsibilities/meanings", "carry weight in our (intellectual) pursuits in new ways", "enter into new relations with each other". Maybe this looks weird to you if you are used to only thinking of words/concepts as things which are supposed to somehow just refer; I suggest that you also see how words/concepts are like [technological components]/[code snippets]/tools which can [make up]/[self-assemble]/[be assembled] into (larger) apparatuses/programs/thoughts/activities — given this, having a corps of dynamic concepts might start to look sensible. ↩︎
That said, assigning probabilities to pretty clear statements is very much a sensible/substantive/useful/real thing — e.g., in the context of prediction markets. ↩︎
Though note that one could also look at arbitrage as an example of this, and there's a case to be made for opening up a new arbitrage route increasing some sort of order/coherence despite putting some structures in a new relation. ↩︎
This is related to it being good to "train" the thinking-system in part "end-to-end". ↩︎
I don't know if I should be fixing a target and then either asking each to do its work or looking for examples of evolution having done that and asking humans to do it (in theses cases, evolution might come up with a thing that also does $100$ other things), or painting the target around some stuff evolution has made and asking humans to make something similar. ↩︎
I mean like, up to the heat death of the universe (if that ends up holding up) or maybe some other limit like that. What I really mean is that there isn't a time of thinking/fooming followed by a time of doing/implementing/enjoying. ↩︎
I wonder if it'd be possible for the relative role of philosophy/[conceptual refactoring]/thought in thinking better to be reduced (compared to e.g. the role of computational resources) in the future (either indefinitely, or for some meaningful period of time). For example, maybe we could imagine a venture-capitalist-culture-spawned entity brazenly shipping a product that wipes them out, followed by that thing brazenly shipping an even mightier product that wipes it out, and so on many times in succession, always moving faster still and in a philosophically unserious fashion and breaking still more things? That said, we could also imagine reasons for the relative role of serious thought to go up in the world — e.g., maybe that'd be good/rational and that's something the weltgeist would realize more when more intelligent, or maybe ideas becoming even easier to distribute is going to continue increasing the relative value of ideas, or maybe better mechanisms capturing the value provided by philosophical ideas are going to come into use, or maybe a singleton could emerge and have an easier time with coordination issues preventing the world from being thought-guided. Anyway, even if there were a tendency in the direction of the relative role of philosophy being reduced in the world, there's probably no tendency for philosophy to be on its way out of the world. (I mean "philosophy" here in some sense that is not that specific to humans — I think philosophy-the-human-thing might indeed be lost soon, sadly (because humans will probably get wiped out by AI, sadly).) ↩︎
or potentially some future more principled measures of this flavor ↩︎
Like, maybe I'd say that the end of thinking/fooming is still further away than $10^{10}$ years of thinking "at the $2024$ rate". ↩︎
There are also various variants of the big alignment endeavor and various variants of these small problems and various other small problems and various finite toy problems with various relations to the big problem. If you have some other choices of interest here, what I say could, mutatis mutandis, still apply to your variants. ↩︎
of course, creating humanity-next-year might be not-fine on some absolute scale because it'll maybe commit suicide with AI or with something else, but it's not like it's more suicidal than humanity-now, so it's "fine" in a relative sense ↩︎
I do not consider this an exhaustive list of systems smarter than humanity which are fine and possible to create. For instance, it could be feasible at some point to create a system which is better than humans at many things and worse than humans at some things, perhaps being slightly smarter than humans when we perform some aggregation across all domains/skills, and which is highly non-human, but which wants to be friends with humans and to become smarter together instead of becoming smarter largely alone, with some nontrivial number of years of fooming together (perhaps after/involving a legitimate reconciliation/merge of that system with humans). But I think such a scenario is very weird/unlikely on our default path. More generally, I think the list I provide plausibly comes much closer to exhausting the space of “solutions” to the small alignment problem than most other current pictures of alignment would suggest. In particular, I think that creating some sort of fine-to-create super-human benefactor/guardian that "sits outside human affairs but supports them"/"looks at the human world from the outside" is quite plausibly going to remain a bad idea forever. (One could try to construct such a world with some humans fooming faster than others and acting as guardians, but I doubt this would actually end up looking much like them acting as guardians (though there could be some promising setup I haven't considered here). I think it would very likely be much better than a universe with a random foom anyway, given that some kind of humanity might be doing very much and getting very far in such a universe — I just doubt it would be (a remotely unconditioned form of) this slower-fooming humanity that the faster-fooming humans were supposed to act as guardians for.) I elaborate on these themes in later notes. ↩︎
in particular, humanity ↩︎
One of my more absurd(ly expressed) hopes with these notes is to (help) push alignment out of its present "(imo) alchemical stage", marked by people attempting to create some sort of ultimate "aligned artifact" — one which would plausibly solve all problems and make life good eternally (and also marked by people attempting to transmute arbitrary cognitive systems into "aligned" ones, though that deserves additional separate discussion). (To clarify: this analogy between the present alignment field and alchemy is not meant as a further argument — it just allows for a sillier restatement of a claim already made.) ↩︎
To say a bit more: I'm unsure about how long a stretch one can reasonably think this about. It obviously depends on the types of capability-gainings involved — for example, there are probably meaningful differences in "safety" between (a) doing algebraic geometry, (b) inventing/discovering probability and beginning to use it in various contexts, (c) adding "neurons" via brain-computer interface and doing some kind of RL-training to set weights so these neurons help you do math (I don't actually have a specific design for this, and it might well be confused/impossible, but try to imagine something like this), and (d) making an AI hoping it will do advanced math for you, even once we "normalize" the items in this comparison so that each "grants the same amount of total capability". These differences can to some extent be gauged ex ante, and at "capability gain parity", there will probably be meaningful selection toward "safer" methods. Also relevant to the question about this "good stretch" (even making sense): the extent to which one's values mostly make sense only "in one's own time". I'm currently confused about these and other relevant background matters, and so lack a clear view of how long a good stretch (starting from various future vantage points) one could reasonably hope for. I think I'd give probability at least $10^{- 6}$ to humanity having a worthwhile future of at least $10^{10}$ "subjective years". ↩︎
But this is plausibly still specification gaming. ↩︎
One could also ask more generally if there is a textbook for making an alien AI which does something delimited-but-transformative (like making mind uploads) and then self-destructs (and doesn't significantly affect the world except via its making of mind uploads, and with the mind upload tech it provides not being malign). ↩︎
though most good futures surely involve us changing radically, and in particular involve a great variety of previously fairly alien AI components being used by/in humanity ↩︎
One can also ask versions where many alien AIs are involved (in parallel or in succession), with some alien AIs being smarter than humanity indefinitely. I'd respond to these versions similarly. ↩︎
That said, I'll admit that even if you agree that alignment isn't the sort of thing that can be solved, you could still think there are good paths forward on which AIs do alignment research for us, indefinitely handling the infinitely rich variety of challenges about how to proceed. I think that this isn't going to work out — that such futures overwhelmingly have AIs doing AI things and basically nothing meaningfully human going on — but I admit that the considerations in these notes up until the present point are insufficient for justifying this. I'll say more about this in later notes. ↩︎
In fact, I don't know of any research making any meaningful amount of progress on the technical challenge of making any AI which is smarter than us and good to make. But also, I think it's plausible we should be doing something much more like becoming smarter ourselves forever instead. These statements call for (further) elaboration and justification, which I aim to provide in upcoming notes in this sequence. ↩︎
I don't mean anything that mysterious here — I largely just mean what I've already said in previous notes, though this theme and the broader them that history won't end could be developed much further (it will be developed a bit further in later notes). ↩︎
Instead of "primitive compositional language", I originally wanted to say "language" here, but since I don't think language is that much of a definite single thing — I think it is a composite of many "ideas", and very open to new "ideas" getting involved — I went with "primitive compositional language", trying to give a slightly less composite thing. But that is surely still not that unitary. ↩︎
or maybe multiple such systems, in parallel or in succession ↩︎
There are also some things made by/of other life (such as a beaver dam and a forest ecosystem) and some things made by physics (such as stars, planets, oceans, volcanoes, clouds). There's often (almost always?) some selection/optimization process going on even to make these structures “of mere physics”. ↩︎

LESSWRONG
LW

LESSWRONG
LW

55

An Advent of Thought

55

Ω 29

55

Ω 29

1 thinking can only be infinitesimally understood^[10]

2 infinitude spreads

3 math, thinking, and technology are equi-infinite

4 general intelligence is not that definite

5 confusion isn't going away

6 thinking (ever better) will continue

7 alignment is infinite

8 making an AI which is broadly smarter than humanity would be most significant

55

An Advent of Thought

55

Ω 29

55

Ω 29

1 thinking can only be infinitesimally understood[10]

2 infinitude spreads

3 math, thinking, and technology are equi-infinite

4 general intelligence is not that definite

5 confusion isn't going away

6 thinking (ever better) will continue

7 alignment is infinite

8 making an AI which is broadly smarter than humanity would be most significant

1 thinking can only be infinitesimally understood^[10]