It seems unlikely that different hastily cobbled-together programs would have the same bug.
Is this true? My sense is that in, for example, Advent of Code problems, different people often write the same bug into their program.
ah, but booby traps in coding puzzles can be deliberate... one might even say that it can feel "rewarding" when we train ourselves on these "adversarial" examples
the phenomenon of programmers introducing similar bugs in similar situations might be fascinating, but I wouldn't expect a clear answer to the question "Is this true?" without a slightly more precise definitions of:
- "same" bug
- same "bug"
- "hastily" cobbled-together programs
- hastily "cobbled-together" programs ...
Adversarial examples suggest to me that by default ML systems don't necessarily learn what we want them to learn:
- They put too much emphasis on high frequency features, suggesting a different inductive bias from humans.
- They don't handle contradictory evidence in a reasonable way, i.e., giving a confident answer when high frequency features (pixel-level details) and low frequency features (overall shape) point to different answers.
The evidence from adversarial training suggests to me that AT is merely patching symptoms (e.g., making the ML system de-emphasize certain specific features) and not fixing the underlying problem. At least this is my impression from watching this video on Adversarial Robustness, specifically the chapters on Adversarial Arms Race and Unforeseen Adversaries.
Aside from this, it's also unclear how to apply AT to your original motivation:
A function that tells your AI system whether an action looks good and is right virtually all of the time on natural inputs isn’t safe if you use it to drive an enormous search for unnatural (highly optimized) inputs on which it might behave very differently.
because in order to apply AT we need a model of what "attacks" the adversary is allowed to do (in this case the "attacker" is a superintelligence trying to optimize the universe, so we have to model it as being allowed to do anything?) and also ground-truth training labels.
For this purpose, I don't think we can use the standard AT practice of assuming that any data point within a certain distance of a human-labeled instance, according to some metric, has the same label as that instance. Suppose we instead let the training process query humans directly for training labels (i.e., how good some situation is) on arbitrary data points, well that's slow/costly if the process isn't very sample efficient (which modern ML isn't), and also scary if human implementations of human values may already have adversarial examples. (The "perceptual wormholes" work and other evidence suggest that humans also aren't 100% adversarially robust.)
My own thinking is that we probably need to go beyond adversarial training for this, along the lines of solving metaphilosophy and then using that solution to find/fix existing adversarial examples and correctly generalize human values out of distribution.
They put too much emphasis on high frequency features, suggesting a different inductive bias from humans.
This was found to not be true at scale! It doesn't even feel that true w/weaker vision transformers, seems specific to convnets. I bet smaller animal brains have similar problems.
Do you know if it is happening naturally from increased scale, or only correlated with scale (people are intentionally trying to correct the "misalignment" between ML and humans of shape vs texture bias by changing aspects of the ML system like its training and architecture, and simultaneously increasing scale)? I somewhat suspect the latter due the existence of a benchmark that the paper seems to target ("humans are at 96% shape / 4% texture bias and ViT-22B-384 achieves a previously unseen 87% shape bias / 13% texture bias").
In either case, it seems kind of bad that it has taken a decade or two to get to this point from when adversarial examples were first noticed, and it's unclear whether other adversarial examples or "misalignment" remain in the vision transformer. If the first transformative AIs don't quite learn the right values due to having a different inductive bias from humans, it may not matter much that 10 years later the problem would be solved.
adversarial examples definitely still exist but they'll look less weird to you because of the shape bias.
anyway this is a random visual model, raw perception without any kind of reflective error correction loop, I'm not sure what you expect it to do differently, or what conclusion you're trying to draw from how it does behave? the inductive bias doesn't precisely match human vision, so it has different mistakes, but as you scale both architectures they become more similar. that's exactly what you'd expect for any approximately Bayesian setup.
the shape bias increasing with scale was definitely conjectured long before it was tested. ML scaling is very recent though,and this experiment was quite expensive. Remember when GPT-2 came out and everyone thought that was a big model? This is an image classifier which is over 10x larger than that. They needed a giant image classification dataset which I don't think even existed 5 years ago.
the inductive bias doesn’t precisely match human vision, so it has different mistakes, but as you scale both architectures they become more similar. that’s exactly what you’d expect for any approximately Bayesian setup.
I can certainly understand that as you scale both architectures, they both make less mistakes on distribution. But do they also generalize out of training distribution more similarly? If so, why? Can you explain this more? (I'm not getting your point from just "approximately Bayesian setup".)
They needed a giant image classification dataset which I don’t think even existed 5 years ago.
This is also confusing/concerning for me. Why would it be necessary or helpful to have such a large dataset to align the shape/texture bias with humans?
But do they also generalize out of training distribution more similarly? If so, why?
Neither of them is going to generalize very well out of distribution, and to the extent they do it will be via looking for features that were present in-distribution. The old adage "to imagine 10-dimensional space, first imagine 3-space, then say 10 really hard".
My guess is that basically every learning system which tractably approximates Bayesian updating on noisy high dimensional data is going to end up with roughly Gaussian OOD behavior. There's been some experiments where (non-adversarially-chosen) OOD samples quickly degrade to uniform prior, but I don't think that's been super robustly studied.
The way humans generalize OOD is not that our visual systems are natively equipped to generalize to contexts they have no way of knowing about, that would be a true violation of no-free-lunch theorems, but that through linguistic reflection & deliberate experimentation some of us can sometimes get a handle on the new domain, and then we use language to communicate that handle to others who come up with things we didn't, etc. OOD generalization is a process at the (sub)cultural & whole-nervous-system level, not something that individual chunks of the brain can do well on their own.
This is also confusing/concerning for me. Why would it be necessary or helpful to have such a large dataset to align the shape/texture bias with humans?
Well it might not be, but you need large datasets to motivate studying large models, as their performance on small datasets like imagenet is often only marginally better.
A 20b param ViT trained on 10m images at 224x224x3 is approximately 1 param for every 75 subpixels, and 2000 params for every image. Classification is an easy enough objective that it very likely just overfits, unless you regularize it a ton, at which point it might still have the expected shape bias at great expense. Training a 20b param model is expensive, I don't think anyone has ever spent that much on a mere imagenet classifier, and public datasets >10x the size of imagenet with any kind of labels only started getting collected in 2021.
To motivate this a bit, humans don't see in frames but let's pretend we do. At 60fps for 12h/day for 10 years, that's nearly 9.5 billion frames. Imagenet is 10 million images. Our visual cortex contains somewhere around 5 billion neurons, which is around 50 trillion parameters (at 1 param / synapse & 10k synapses / neuron, which is a number I remember being reasonable for the whole brain but vision might be 1 or 2 OOM special in either direction).
Because of the strange loopy nature of concepts/language/self/different problems metaphilosophy seems unsolvable?
Asking: What is good? already implies that there are the concepts "good", "what", "being" that there are answers and questions ... Now we could ask what concepts or questions to use instead ...
Similarly:
> "What are all the things we can do with the things we have and what decision-making process will we use and why use that process if the character of the different processes is the production of different ends; don't we have to know which end is desired in order to choose the decision-making process that also arrives at that result?"
> Which leads back to desire and knowing what you want without needing a system to tell you what you want.
It's all empty in the Buddhist sense. It all depends on which concepts or turing machines or which physical laws you start with.
They put too much emphasis on high frequency features, suggesting a different inductive bias from humans.
Could you fix this part by adding high frequency noise to the images prior to training? Maybe lots of copies of each image with different noise patterns?
In "Adversarial Spheres", Justin Gilmer et al. investigated a simple synthetic dataset of two classes representing points on the surface of two concentric n-dimensional spheres of radiuses 1 and (an arbitrarily chosen) 1.3. For an architecture yielding an ellipsoidal decision boundary, training on a million datapoints produced a network with very high accuracy (no errors in 10 million samples), but for which most of the axes of the decision ellipsoid were wrong, lying inside the inner sphere or outside the outer sphere—implying the existence of on-distribution adversarial examples (points on one sphere classified by the network as belonging to the other).
One thing I wonder is whether real-world category boundaries tend to be smooth like this, for the kinds of categorizations that are likely to be salient. The categories I tend to care about in practice seem to be things like "is this business plan profitable". If you take a bunch of business plans, and rate them on a scale of -1 to +1 on a bunch of different metrics, and classify whether businesses following them were profitable vs unprofitable, In that case, I wouldn't particularly expect that the boundary between "profitable business plan" and "unprofitable-business-plan" would look like "an ellipsoidal shell centered around some prototypical ur-business-plan, where any business plan inside that shell is profitable and any business plan outside that shell is unprofitable".
I agree, but I don't see why that's relevant? The point of the "Adversarial Spheres" paper is not that the dataset is realistic, of course, but that studying an unrealistically simple dataset might offer generalizable insights. If the ground truth decision boundary is a sphere, but your neural net learns a "squiggly" ellipsoid that admits adversarial examples (because SGD is just brute-forcing a fit rather than doing something principled that could notice hypotheses on the order of, "hey, it's a sphere"), that's a clue that when the ground truth is something complicated, your neural net is also going to learn something squiggly that admits adversarial examples (where the squiggles in your decision boundary predictably won't match the complications in your dataset, even though they're both not-simple).
My suspicion is that for a lot of categorization problems we care about, there isn't a nice smooth boundary between categories such that an adversarially robust classifier is possible, so the failure of the "lol stack more layers" approach to find such boundaries in the rare cases where those boundaries do exist isn't super impactful.
Strong belief weakly held on the "most real-world category boundaries are not smooth".
Sorry, this doesn't make sense to me. The boundary doesn't need to be smooth in an absolute sense in order to exist and be learnable (whether by neural nets or something else). There exists a function from business plans to their profitability. The worry is that if you try to approximate that function with standard ML tools, then even if your approximation is highly accurate on any normal business plan, it's not hard to construct an artificial plan on which it won't be. But this seems like a limitation of the tools; I don't think it's because the space of business plans is inherently fractally complex and unmodelable.
I genuinely think that the space of "what level of success will a business have if it follows its business plan" is inherently fractal in the same way that "which root of a polynomial will repeated iteration of Newton's method converge to" is inherently fractal. For some plans, a tiny change to the plan can lead to a tiny change in behavior, which can lead to a giant change in outcome.
Which is to say "it is, at most points it doesn't matter that it is, but if the point is adversarially selected you once again have to care".
All that said, this is a testable hypothesis. I can't control the entire world closely enough to run tiny variations on a business plan and plot the results on a chart, but I could do something like "take the stable diffusion text encoder, encode three different prompts (e.g. 'a horse', 'a salad bowl', 'a mountain') and then, holding the input noise steady, generate an image for each blend, classify the output images, and plot the results". Do you have strong intuitions about what the output chart would look like?
I actually kind of expect this.
Basically, I think that we should expect a lot of SGD results to result in weights that do serial processing on inputs, refining and reshaping the content into twisted and rotated and stretched high dimensional spaces SUCH THAT those spaces enable simple cutoff based reasoning to "kinda really just work".
Like the prototypical business plan needs to explain "enough" how something is made (cheaply) and then explain "enough" how it will be sold (for more money) over time with improvements in the process (according to some growth rate?) with leftover money going back to investors (with corporate governance hewing to known-robust patterns for enabling the excess to be redirected to early investors rather than to managers who did a corruption coup, or a union of workers that isn't interested in sharing with investors and would plausibly decide play the dictator game at the end in an unfair way, or whatever). So if the "governance", "growth rate", "cost", and "sales" dimensions go into certain regions of the parameter space, each one could strongly contribute to a "don't invest" signal, but if they are all in the green zone then you invest... and that's that?
If, after reading this, you still disagree, I wonder if it is more because (1) you don't think that SGD can find space stretching algorithms with that much semantic flexibility or because (2) you don't think any list of less than 20 concepts like this could be found whose thresholds could properly act as gates on an algorithm for making prudent startup investment decisions... or is it something totally else you don't buy (and if so, what)?
Basically, I think that we should expect a lot of SGD results to result in weights that do serial processing on inputs, refining and reshaping the content into twisted and rotated and stretched high dimensional spaces SUCH THAT those spaces enable simply cutoff based reasoning to "kinda really just work".
I mostly agree with that. I expect that the SGD approach will tend to find transformations that tend to stretch and distort the possibility space such that non-adversarially-selected instances of one class are almost perfectly linearly separable from non-adversarially-selected instances of another class.
My intuition is that stacking a bunch of linear-transform-plus-nonlinearity layers on top of each other lets you hammer something that looks like the chart on the left into something that looks like the chart on the right (apologies for the potato quality illustration)

As such, I think the linear separability comes from the power of the "lol stack more layers" approach, not from some intrinsic simple structure of the underlying data. As such, I don't expect very much success for approaches that look like "let's try to come up with a small set of if/else statements that cleave the categories at the joints instead of inelegantly piling learned heuristics on top of each other".
So if the "governance", "growth rate", "cost", and "sales" dimensions go into certain regions of the parameter space, each one could strongly contribute to a "don't invest" signal, but if they are all in the green zone then you invest... and that's that?
I think that such a model would do quite a bit better than chance. I don't think that such a model would succeed because it "cleaves reality at the joints" though, I expect it would succeed because you've managed to find a way that "better than chance" is good enough and you don't need to make arbitrarily good predictions. Perfectly fine if you're a venture capitalist, not so great if you're seeking adversarial robustness.
I appreciate this response because it stirred up a lot of possible responses, in me, in lots of different directions, that all somehow seems germane to the core goal of securing a Win Conditions for the sapient metacivilization of earth! <3
(A) Physical reality is probably hyper-computational, but also probably amenable to pulling a nearly infinite stack of "big salient features" from a reductively analyzable real world situation.
My intuition says that this STOPS being "relevant to human interests" (except for modern material engineering and material prosperity and so on) roughly below the level of "the cell".
Other physics with other biochemistry could exist, and I don't think any human would "really care"?
Suppose a Benevolent SAI had already replaced all of our cells with nanobots without our permission AND without us noticing because it wanted to have "backups" or something like that...
(The AI in TMOPI does this much less elegantly, because everything in that story is full of hacks and stupidity. The overall fact that "everything is full of hacks and stupidity" is basically one of the themes of that novel.)
Contingent on a Benevoent SAI having thought it had good reason to do such a thing, I don't think that once we fully understand the argument in favor of doing it that we would really have much basis for objecting?
But I don't know for sure, one way or the other...
((To be clear, in this hypothetical, I think I'd volunteer to accept the extra risk to be one of the last who was "Saved" this way, and I'd volunteer to keep the secret, and help in a QA loop of grounded human perceptual feedback, to see if some subtle spark of magical-somethingness had been lost in everyone transformed this way? Like... like hypothetically "quantum consciousness" might be a real thing, and maybe people switched over to running atop "greygoo" instead of our default "pinkgoo" changes how "quantum consciousness" works and so the changeover would non-obviously involve a huge cognitive holocaust of sorts? But maybe not! Experiments might be called for... and they might need informed consent? ...and I think I'd probably consent to be in "the control group that is unblinded as part of the later stages of the testing process" but I would have a LOT of questions before I gave consent to something Big And Smart that respected "my puny human capacity to even be informed, and 'consent' in some limited and animal-like way".))
What I'm saying is: I think maybe NORMAL human values (amongst people with default mental patterns rather than weirdo autists who try to actually be philosophically coherent and ended up with utility functions that have coherently and intentionally unbounded upsides) might well be finite, and a rule for granting normal humans a perceptually indistinguishable version of "heaven" might be quite OK to approximate with "a mere a few billion well chosen if/then statements".
To be clear, the above is a response to this bit:
As such, I think the linear separability comes from the power of the "lol stack more layers" approach, not from some intrinsic simple structure of the underlying data. As such, I don't expect very much success for approaches that look like "let's try to come up with a small set of if/else statements that cleave the categories at the joints instead of inelegantly piling learned heuristics on top of each other".
And:
I don't think that such a model would succeed because it "cleaves reality at the joints" though, I expect it would succeed because you've managed to find a way that "better than chance" is good enough and you don't need to make arbitrarily good predictions.
Basically, I think "good enough" might be "good enough" for persons with finite utility functions?
(B) A completely OTHER response here is that you should probably take care to NOT aim for something that is literally mathematically impossible...
Unless this is part of some clever long term cognitive strategy, where you try to prove one crazy extreme, and then its negation, back and forth, as a sort of "personally implemented GAN research process" (and even then?!)...
...you should probably not spend much time trying to "prove that 1+1=5" nor try to "prove that the Halting Problem actually has a solution". Personally, any time I reduce a given plan to "oh, this is just the Halting Problem again" I tend to abandon that line of work.
Perfectly fine if you're a venture capitalist, not so great if you're seeking adversarial robustness.
Past a certain point, one can simply never be adversarially robust in a programmatic and symbolically expressible way.
Humans would have to have non-Turing-Complete souls, and so would any hypothetical Corrigible Robot Saint/Slaves, in order to literally 100% prove that literally infinite computational power won't find a way to make things horrible.
There is no such thing as a finitely expressible "Halt if Evil" algorithm...
...unless (I think?) all "agents" involved are definitely not Turing Complete and have no emotional attachments to any questions whose answers partake of the challenges of working with Turing Complete systems? And maybe someone other than me is somehow smart enough to write a model of "all the physics we care about" and "human souls" and "the AI" all in some dependently typed language that will only compile if the compiler can generate and verify a "proof that each program, and ALL programs interacting with each other, halt on all possible inputs"?
My hunch is that that effort will fail, over and over, forever, but I don't have a good clean proof that it will fail.
Note that I'm pretty sure A and B are incompatible takes.
In "take A" I'm working from human subjectivity "down towards physics (through a vast stack of sociology and biology and so on)" and it just kinda seems like physics is safe to throw away because human souls and our humanistically normal concerns are probably mostly pretty "computational paltry" and merely about securing food, and safety, and having OK romantic lives?
In "take B" I'm starting with the material that mathematicians care about, and noticing that it means the project is doomed if the requirement is to have a mathematical proof about all mathematically expressible cares or concerns.
It would be... kinda funny, maybe, to end up believing "we can secure a Win Condition for the Normies (because take A is basically true), but True Mathematicians are doomed-and-blessed-at-the-same-time to eternal recursive yearning and Real Risk (because take B is also basically true)" <3
(C) Chaos is a thing! Even (and especially) in big equations, including the equations of mind that big stacks of adversarially optimized matrices represent!
This isn't a "logically deep" point. I'm just vibing with your picture where you imagine that the "turbulent looking" thing is a metaphor for reality.
In observable practice, the boundary conditions of the equations of AI also look like fractally beautiful turbulence!
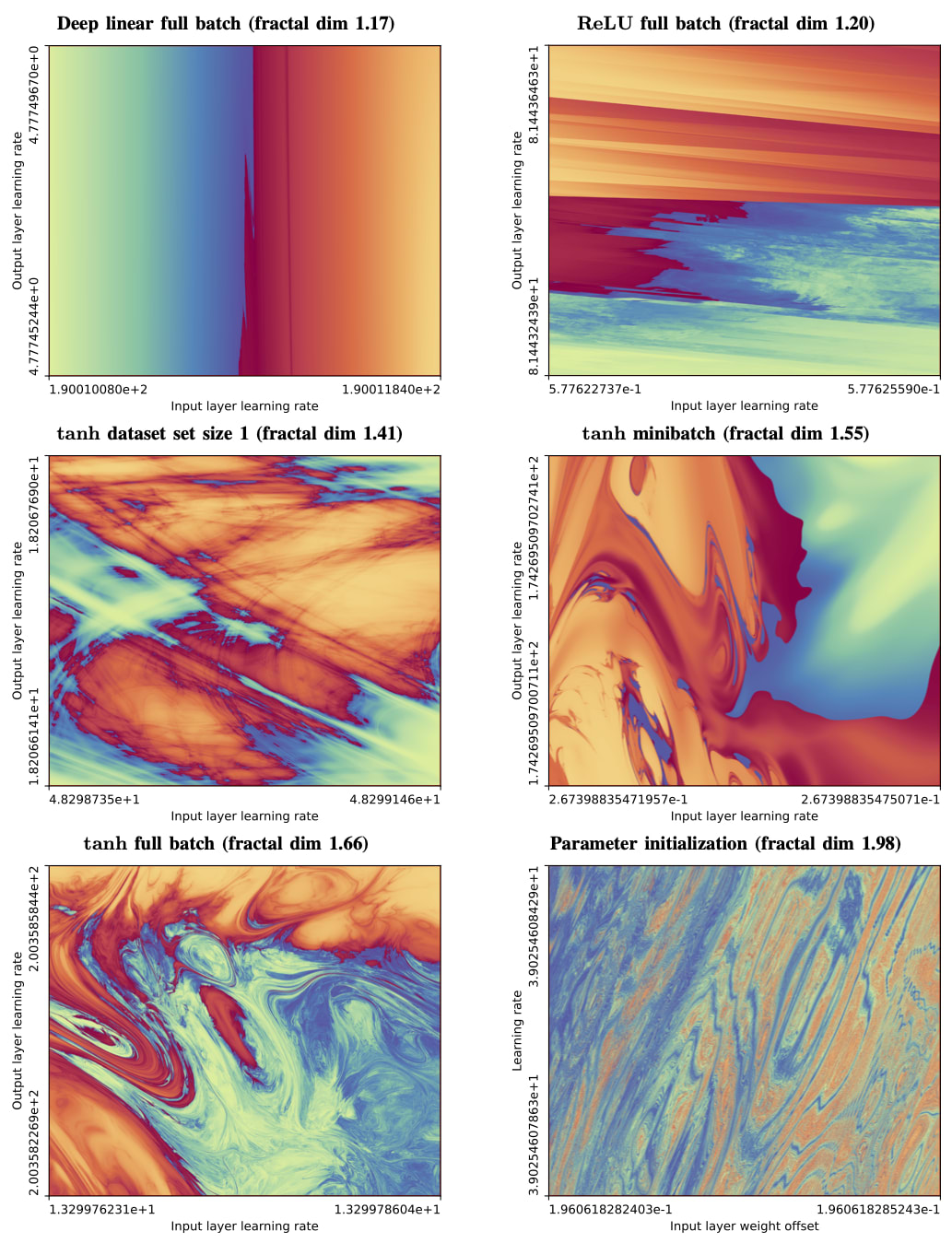
I predict that you will be surprised by this empirical result. Here is the "high church papering" of the result:
TITLE: The boundary of neural network trainability is fractal
Abstract: Some fractals -- for instance those associated with the Mandelbrot and quadratic Julia sets -- are computed by iterating a function, and identifying the boundary between hyperparameters for which the resulting series diverges or remains bounded. Neural network training similarly involves iterating an update function (e.g. repeated steps of gradient descent), can result in convergent or divergent behavior, and can be extremely sensitive to small changes in hyperparameters. Motivated by these similarities, we experimentally examine the boundary between neural network hyperparameters that lead to stable and divergent training. We find that this boundary is fractal over more than ten decades of scale in all tested configurations.
Also, if you want to deep dive on some "half-assed peer review of this work" hacker news chatted with itself about this paper at length.
EDITED TO ADD: You respond "Lots of food for thought here, I've got some responses brewing but it might be a little bit" and I am happy to wait. Quality over speed is probably maybe still sorta correct. Timelines are compressing, but not so much that minutes matter... yet?
Alright, it's been more than a "little" bit (new baby, haven't had a ton of time), and not as complete of a reply as I was hoping to write, but
(A) Physical reality is probably hyper-computational
My impression is almost the opposite - physical reality seems not only to contain a finite amount of information and have a finite capacity for processing that information, but on top of that the "finite" in question seems surprisingly small. Specifically, the entropy of the observable universe seems to be in the ballpark of bits (, , so area is given by . The Planck length is and thus the Bekenstein–Hawking entropy in natural units is just ). For context, the best estimate I've seen is that the total amount of data stored by humanity is in the ballpark of bits. If data storage increases exponentially, we're a fifth of the way to "no more data storage capacity in the universe". And similarly Landauer gives pretty tight bounds on computational capacity (I think something on the order of bit erasures as an upper bound if my math checks out).
So the numbers are large, but not "you couldn't fit the number on a page if you tried to write it out" large.
but also probably amenable to pulling a nearly infinite stack of "big salient features" from a reductively analyzable real world situation
If we're limiting it to "big salient features" I expect the number of features one actually cares about in a normal situation is actually pretty small. Deciding which features are relevant, though, can be nontrivial.
What I'm saying is: I think maybe NORMAL human values (amongst people with default mental patterns rather than weirdo autists who try to actually be philosophically coherent and ended up with utility functions that have coherently and intentionally unbounded upsides) might well be finite, and a rule for granting normal humans a perceptually indistinguishable version of "heaven" might be quite OK to approximate with "a mere a few billion well chosen if/then statements".
I don't disagree that a few billion if/then statements are likely sufficient. There's a sense in which e.g. the MLP layers of an LLM are just doing a few tens of millions "if residual > value in this direction then write value in that direction, else noop" operations, which might be using clever-high-dimensional-space-tricks to emulate doing a few billion such operations, and they are able to answer questions about human values in a sane way, so it's not like those values are intractable to express.
The rules for a policy that achieves arbitrarily good outcomes according to that relatively-compactly-specifiable value system, however, might not admit "a few billion well-chosen if/then statements". For example it's pretty easy to specify "earning block reward for the next bitcoin block would be good" but you can't have a few billion if/then statements which will tell you what nonce to choose such that the hash of the resulting block has enough zeros to earn the block reward.
If I had to condense it down to one sentence it would be "the hard part of consequentialism is figuring out tractable rules which result in good outcomes when applied, not in figuring out which outcomes are even good".
(B) A completely OTHER response here is that you should probably take care to NOT aim for something that is literally mathematically impossible...
Agreed. I would go further than "not literally mathematically impossible" and further specify "and also not trying to find a fully optimal solution for an exponentially hard problem with large n".
Past a certain point, one can simply never be adversarially robust in a programmatic and symbolically expressible way.
Beautifully put. I suspect that "certain point" is one of those "any points we actually care about are way past this point" things.
(C) Chaos is a thing! Even (and especially) in big equations, including the equations of mind that big stacks of adversarially optimized matrices represent!
"The boundary of neural network trainability is fractal" was a significant part of my inspiration for writing the above. Honestly, if I ever get some nice contiguous more-than-1-hour chunks of time I'd like to write a post along the lines of "sometimes there are no neat joints separating clusters in thing-space" which emphasizes that point (my favorite concrete example is that "predict which complex root of a cubic or higher polynomial Euler's method will converge to given a starting value" generates a fractal rather than the voronoi-diagram-looking-thing you would naively expect).
It would be... kinda funny, maybe, to end up believing "we can secure a Win Condition for the Normies (because take A is basically true), but True Mathematicians are doomed-and-blessed-at-the-same-time to eternal recursive yearning and Real Risk (because take B is also basically true)" <3
I think this is likely true. Though I think there are probably not that many True Mathematicians once the people who have sought and found comfort in math find that they can also seek and find comfort outside of math.
Quality over speed is probably maybe still sorta correct
Don't worry, the speed was low but the quality was on par with it :)
A function that tells your AI system whether an action looks good and is right virtually all of the time on natural inputs isn't safe if you use it to drive an enormous search for unnatural (highly optimized) inputs on which it might behave very differently.
Yeah, you can have something which is “a brilliant out-of-the-box solution to a tricky problem” from the AI’s perspective, but is “reward-hacking / Goodharting the value function” from the programmer’s perspective. You say tomato, I say to-mah-to.
It’s tricky because there’s economic pressure to make AIs that will find and execute brilliant out-of-the-box solutions. But we want our AIs to think outside of some of the boxes (e.g. yes you can repurpose a spare server rack frame for makeshift cable guides), but we want it to definitely stay inside other boxes (e.g. no you can’t take over the world). Unfortunately, the whole idea of “think outside the box” is that we’re not aware of all the boxes that we’re thinking inside of.
The particular failure mode of "leaving one thing out" is starting to seem less likely on the current paradigm. Katja Grace notes that image synthesis methods have no trouble generating photorealistic human faces. Diffusion models don't "accidentally forget" that faces have nostrils, even if a human programmer trying to manually write a face image generation routine might. Similarly, large language models obey the quantity-opinion-size-age-shape-color-origin-purpose adjective order convention in English without the system designers needing to explicitly program that in or even be aware of it, despite the intuitive appeal of philosophical arguments one could make to the effect that "English is fragile."
All three of those examples are of the form “hey here’s a lot of samples from a distribution, please output another sample from the same distribution”, which is not the kind of problem where anyone would ever expect adversarial dynamics / weird edge-cases, right?
(…Unless you do conditional sampling of a learned distribution, where you constrain the samples to be in a specific a-priori-extremely-unlikely subspace, in which case sampling becomes isomorphic to optimization in theory. (Because you can sample from the distribution of (reward, trajectory) pairs conditional on high reward.))
Or maybe you were making a different point in this particular paragraph?
(…Unless you do conditional sampling of a learned distribution, where you constrain the samples to be in a specific a-priori-extremely-unlikely subspace, in which case sampling becomes isomorphic to optimization in theory. (Because you can sample from the distribution of (reward, trajectory) pairs conditional on high reward.))
Does this isomorphism actually go through? I know decision transformers kinda-sorta show how you can do optimization-through-conditioning in practice, but in theory the loss function which you use to learn the distribution doesn't constrain the results of conditioning off-distribution, so I'd think you're mainly relying on having picked a good architecture which generalizes nicely out of distribution.
Let D be the distribution of (reward, trajectory) pairs for every possible trajectory.
Split D into two subsets: D1 where reward > 7 and D2 where reward ≤ 7.
Suppose that, in D, 1-in-a-googol samples is in the subset D1, and all the rest are in D2.
(For example, if a videogame involves pressing buttons for 20 minutes, you can easily have less than 1-in-a-googol chance of beating even the first mini-boss if you press the buttons randomly.)
Now we randomly pick a million samples from D in an attempt to learn the distribution D. But (as expected with overwhelming probability), it turns out that every single one of those million samples are more specifically in the subset D2.
Now consider a point X in D1 (its reward is 30). Question: Is X “out of distribution”?
Arguably no, because we set up a procedure to learn the distribution D, and D contains X.
Arguably yes, because when we ran the procedure, all the points actually used to learn the distribution were in D2, so we were kinda really only learning D2, and D2 doesn’t contain X.
(In the videogame example, if in training you never see a run that gets past the first mini-boss, then certainly intuitively we'd say that runs that do get past it, and that thus get to the next stage of the game, are OOD.)
Anyway, I was gonna say the opposite of what you said—sufficiently hard optimization via conditional sampling works in theory (i.e., if you could somehow learn D and conditionally sample on reward>7, it would work), but not in practice (because reward>7 is so hard to come by that you will never actually learn that part of D by random sampling).
The way I'd phrase the theoretical problem when you fit a model to a distribution (e.g. minimizing KL-divergence on a set of samples), you can often prove theorems of the form "the fitted-distribution has such-and-such relationship to the true distribution", e.g. you can compute confidence intervals for parameters and predictions in linear regression.
Often, all that is sufficient for those theorems to hold is:
- The model is at an optimum
- The model is flexible enough
- The sample size is big enough
... because then if you have some point X you want to make predictions for, the sample size being big enough means you have a whole bunch of points in the empirical distribution that are similar to X. These points affect the loss landscape, and because you've got a flexible optimal model, that forces the model to approximate them well enough.
But this "you've got a bunch of empirical points dragging the loss around in relevant ways" part only works on-distribution, because you don't have a bunch of empirical points from off-distribution data. Even if technically they form an exponentially small slice of the true distribution, this means they only have an exponentially small effect on the loss function, and therefore being at an optimal loss is exponentially weakly informative about these points.
(Obviously this is somewhat complicated by overfitting, double descent, etc., but I think the gist of the argument goes through.)
I guess it depends on whether one makes the cut between theory and practice with or without assuming that one has learned the distribution? I.e. I'm saying if you have a distribution D, take some samples E, and approximate E with Q, then you might be able to prove that samples from Q are similar to samples from D, but you can't prove that conditioning on something exponentially unlikely in D gives you something reasonable in Q. Meanwhile you're saying that conditioning on something exponentially unlikely in D is tantamount to optimization.
All three of those examples are of the form “hey here’s a lot of samples from a distribution, please output another sample from the same distribution”, which is not the kind of problem where anyone would ever expect adversarial dynamics / weird edge-cases, right?
I would expect some adversarial dynamics/weird edge cases in such cases. The International Obfuscated C Code Contest is a thing that exists, and so a sequence predictor that has been trained to produce content similar to an input distribution that included the entrants to that contest will place some nonzero level of probability that the C code it writes should actually contain a sneaky backdoor, and, once the sneaky backdoor is there, would place a fairly high probability that the next token it outputs should be another part of the same program.
Such weird/adversarial outputs probably won't be a super large part of your input space unless you're sampling in such a way as to make them overrepresented, though.
Unless you do conditional sampling of a learned distribution, where you constrain the samples to be in a specific a-priori-extremely-unlikely subspace, in which case sampling becomes isomorphic to optimization in theory
Right. I think the optimists would say that conditional sampling works great in practice, and that this bodes well for applying similar techniques to more ambitious domains. There's no chance of this image being in the Stable Diffusion pretraining set:
One could reply, "Oh, sure, it's obvious that you can conditionally sample a learned distribution to safely do all sorts of economically valuable cognitive tasks, but that's not the danger of true AGI." And I ultimately think you're correct about that. But I don't think the conditional-sampling thing was obvious in 2004.
One could reply, "Oh, sure, it's obvious that you can conditionally sample a learned distribution to safely do all sorts of economically valuable cognitive tasks, but that's not the danger of true AGI." And I ultimately think you're correct about that. But I don't think the conditional-sampling thing was obvious in 2004.
Idk. We already knew that you could use basic regression and singular vector methods to do lots of economically valuable tasks, since that was something that was done in 2004. Conditional-sampling "just" adds in the noise around these sorts of methods, so it goes to say that this might work too.
Adding noise obviously doesn't matter in 1 dimension except for making the outcomes worse. The reason we use it for e.g. images is that adding the noise does matter in high-dimensional spaces because without the noise you end up with the highest-probability outcome, which is out of distribution. So in a way it seems like a relatively minor fix to generalize something we already knew was profitable in lots of cases.
On the other hand, I didn't learn the probability thing until playing with some neural network ideas for outlier detection and learning they didn't work. So in that sense it's literally true that it wasn't obvious (to a lot of people) back before deep learning took off.
And I can't deny that people were surprised that neural networks could learn to do art. To me this became relatively obvious with early GANs, which were later than 2004 but earlier than most people updated on it.
So basically I don't disagree but in retrospect it doesn't seem that shocking.
Katja Grace notes that image synthesis methods have no trouble generating photorealistic human faces.
They're terrible at hands though (which has ruined many otherwise good images for me). That post used Stable Diffusion 1.5, but even the latest SD 3.0 (with versions 2.0, 2.1, XL, Stable Cascade in between) is still terrible at it.
Don't really know how relevant this is to your point/question about fragility of human values, but thought I'd mention it since it seems plausibly as relevant as AIs being able to generate photorealistic human faces.
I think it actually points to convergence between human and NN learning dynamics. Human visual cortices are also bad at hands and text, to the point that lucid dreamers often look for issues with their hands / nearby text to check whether they're dreaming.
One issue that I think causes people to underestimate the degree of convergence between brain and NN learning is to compare the behaviors of entire brains to the behaviors of individual NNs. Brains consist of many different regions which are "trained" on different internal objectives, then interact with each other to collectively produce human outputs. In contrast, most current NNs contain only one "region", which is all trained on the single objective of imitating certain subsets of human behaviors.
We should thus expect NN learning dynamics to most resemble those of single brain regions, and that the best match for humanlike generalization patterns will arise from putting together multiple NNs that interact with each other in a similar manner as human brain regions.
Scale basically solves this too, with some other additions (not part of any released version of MJ yet) really putting a nail in the coffin, but I can't say too much here w/o divulging trade secrets. I can say that I'm surprised to hear that SD3 is still so much worse than Dalle3, Ideogram on that front - I wonder if they just didn't train it long enough?
Great post. I wonder how to determine what is a "reasonable" maximum epsilon to use in the adversarial training. Does performance on normal examples get worse as epsilon increases?
An interesting question! I looked in “Towards Deep Learning Models Resistant to Adversarial Attacks” to see what they had to say on the question. If I’m interpreting their Figure 6 correctly, there’s a negligible increase in error rate as epsilon increases, and then at some point the error rate starts swooping up toward 100%. The transition seems to be about where the perturbed images start to be able to fool humans. (Or perhaps slightly before.). So you can’t really blame the model for being fooled, in that case. If I had to pick an epsilon to train with, I would pick one just below the transition point, where robustness is maximized without getting into the crazy zone.
All this is the result of a cursory inspection of a couple of papers. There’s about a 30% chance I’ve misunderstood.
I'm impressed by Gaziv et al's "adversarial examples that work on humans" enough to not pause and carefully read the paper, but rather to speculate on how it could be a platform for building things :-)
The specific thing that jumped to mind is Davidad's current request for proposals looking to build up formal languages within which to deploy "imprecise probability" formalisms such that AI system outputs could come with proofs about safely hitting human expressible goals, in these languages, like "solve global warming" while still "avoiding extinction, genocide, poverty, or other dystopian side effects".
I don't know that there is necessarily a lot of overlap in the vocabularies of these two efforts... yet? But the pictures in my head suggest that the math might not actually be that different. There's going to be a lot of "lines and boundaries and paths in a high dimensional space" mixed with fuzzing operations, to try to regularize things until the math itself starts to better match out intuitions around meaning and safety and so on.
Just to focus on the underlying tension, does this differ from noting "all models are wrong, some models are useful"?
an AI designer from a more competent civilization would use a principled understanding of vision to come up with something much better than what we get by shoveling compute into SGD
How sure are you that there can be a "principled understanding of vision" that leads to perfect modeling, as opposed to just different tradeoffs (of domain, precision, recall, cost, and error cases)? The human brain is pretty susceptible to adversarial (both generated illusion and evolved camoflage) inputs as well, though they're different enough that the specific failures aren't comparable.
On this view, adversarial examples arise from gradient descent being "too smart", not "too dumb": the program is fine; if the test suite didn't imply the behavior we wanted, that's our problem.
Shouldn't we expect to see RL models trained purely on self play not to have these issues then?
My understanding is that even models trained primarily with self play, such as katago, are vulnurable to adversarial attacks. If RL models are vulnurable to the same type of adversarial attacks, isn't that evidence against this theory?
The LessWrong Review runs every year to select the posts that have most stood the test of time. This post is not yet eligible for review, but will be at the end of 2025. The top fifty or so posts are featured prominently on the site throughout the year.
Hopefully, the review is better than karma at judging enduring value. If we have accurate prediction markets on the review results, maybe we can have better incentives on LessWrong today. Will this post make the top fifty?


Adversarial Examples: A Problem
The apparent successes of the deep learning revolution conceal a dark underbelly. It may seem that we now know how to get computers to (say) check whether a photo is of a bird, but this façade of seemingly good performance is belied by the existence of adversarial examples—specially prepared data that looks ordinary to humans, but is seen radically differently by machine learning models.
The differentiable nature of neural networks, which make them possible to be trained at all, are also responsible for their downfall at the hands of an adversary. Deep learning models are fit using stochastic gradient descent (SGD) to approximate the function between expected inputs and outputs. Given an input, an expected output, and a loss function (which measures "how bad" it is for the actual output to differ from the expected output), we can calculate the gradient of the loss on the input—the derivative with respect to every parameter in our neural network—which tells us which direction to adjust the parameters in order to make the loss go down, to make the approximation better.[1]
But gradients are a double-edged sword: the same properties that make it easy to calculate how to adjust a model to make it better at classifying an image, also make it easy to calculate how to adjust an image to make the model classify it incorrectly. If we take the gradient of the loss with respect to the pixels of the image (rather than the parameters of the model), that tells us which direction to adjust the pixels to make the loss go down—or up. (The direction of steepest increase is just the opposite of the direction of steepest decrease.) A tiny step in that direction in imagespace perturbs the pixels of an image just so—making this one the tiniest bit darker, that one the tiniest bit lighter—in a way that humans don't even notice, but which completely breaks an image classifier sensitive to that direction in the conjunction of many pixel-dimensions, making it report utmost confidence in nonsense classifications.
Some might ask: why does it matter if our image classifier fails on examples that have been mathematically constructed to fool it? If it works for the images one would naturally encounter, isn't that good enough?
One might mundanely reply that gracefully handling untrusted inputs is a desideratum for many real-world applications, but a more forward-thinking reply might instead emphasize what adversarial examples imply about our lack of understanding of the systems we're building, separately from whether we pragmatically expect to face an adversary. It's a problem if we think we've trained our machines to recognize birds, but they've actually learned to recognize a squiggly alien set in imagespace that includes a lot of obvious non-birds and excludes a lot of obvious birds. To plan good outcomes, we need to understand what's going on, and "The loss happens to increase in this direction" is at best only the start of a real explanation.
One obvious first guess as to what's going on is that the models are overfitting. Gradient descent isn't exactly a sophisticated algorithm. There's an intuition that the first solution that you happen to find by climbing down the loss landscape is likely to have idiosyncratic quirks on any inputs it wasn't trained for. (And that an AI designer from a more competent civilization would use a principled understanding of vision to come up with something much better than what we get by shoveling compute into SGD.) Similarly, a hastily cobbled-together conventional computer program that passed a test suite is going to have bugs in areas not covered by the tests.
But that explanation is in tension with other evidence, like the observation that adversarial examples often generalize between models. (An adversarial example optimized against one model is often misclassified by others, too, and even assigned the same class.) It seems unlikely that different hastily cobbled-together programs would have the same bug.
In "Adversarial Examples Are Not Bugs, They Are Features", Andrew Ilyas et al. propose an alternative explanation, that adversarial examples arise from predictively useful features that happen to not be robust to "pixel-level" perturbations. As far as the in-distribution predictive accuracy of the model is concerned, a high-frequency pattern that humans don't notice is fair game for distinguishing between image classes; there's no rule that the features that happen to be salient to humans need to take priority. Ilyas et al. provide some striking evidence for this thesis in the form of a model trained exclusively on adversarial examples yielding good performance on the original, unmodified test set (!!).[2] On this view, adversarial examples arise from gradient descent being "too smart", not "too dumb": the program is fine; if the test suite didn't imply the behavior we wanted, that's our problem.
On the other hand, there's also some evidence that gradient descent being "dumb" may play a role in adversarial examples, in conjunction with the counterintuitive properties of high-dimensional spaces. In "Adversarial Spheres", Justin Gilmer et al. investigated a simple synthetic dataset of two classes representing points on the surface of two concentric n-dimensional spheres of radiuses 1 and (an arbitrarily chosen) 1.3. For an architecture yielding an ellipsoidal decision boundary, training on a million datapoints produced a network with very high accuracy (no errors in 10 million samples), but for which most of the axes of the decision ellipsoid were wrong, lying inside the inner sphere or outside the outer sphere—implying the existence of on-distribution adversarial examples (points on one sphere classified by the network as belonging to the other). In high-dimensional space, pinning down the exact contours of the decision boundary is bigger ask of SGD than merely being right virtually all of the time—even though a human wouldn't take a million datapoints to notice the hypothesis, "Hey, these all have a norm of exactly either 1 or 1.3."
Adversarial Training: A Solution?
Our story so far: we used gradient-based optimization to find a neural network that seemed to get low loss on an image classification task—that is, until an adversary used gradient-based optimization to find images on which our network gets high loss instead. Is that the end of the story? Are neural networks just the wrong idea for computer vision after all, or is there some way to continue within the current paradigm?
Would you believe that the solution involves ... gradient-based optimization?
In "Towards Deep Learning Models Resistant to Adversarial Attacks", Aleksander Madry et al. provide a formalization of the problem of adversarially robust classifiers. Instead of just trying to find network parameters θ that minimize loss L on an input x of intended class y, as in the original image classification task, the designers of a robust classifier are trying to minimize loss on inputs with a perturbation δ crafted by an adversary trying to maximize loss (subject to some maximum perturbation size ε):
minθmax||δ||<εL(θ,x+δ,y)
In this formulation, the attacker's problem of creating adversarial examples, and the defender's problem of training a model robust to them, are intimately related. If we change the image-classification problem statement to be about correctly classifying not just natural images, but an ε-ball around them, then you've defeated all adversarial examples up to that ε. This turns out to generally require larger models than the classification problem for natural images: evidently, the decision boundary needed to separate famously "spiky" high-dimensional balls is significantly more complicated than that needed to separate natural inputs as points.
To solve the inner maximization problem, Madry et al. use the method of projected gradient descent (PGD) for constrained optimization: do SGD on the unconstrained problem, but after every step, project the result onto the constraint (in this case, the set of perturbations of size less than ε). This is somewhat more sophisticated than just generating any old adversarial examples and throwing them into your training set; the iterative aspect of PGD makes a difference.
Adversarial Robustness Is About Aligning Human and Model Decision Boundaries
What would it look like if we succeeded at training an adversarially robust classifier? How would you know if it worked? It's all well and good to say that a classifier is robust if there are no adversarial examples: you shouldn't be able to add barely-perceptible noise to an image and completely change the classification. But by the nature of the problem, adversarial examples aren't machine-checkable. We can't write a function that either finds them or reports "No solution found." The machine can only optimize for inputs that maximize loss. We, the humans, call such inputs "adversarial examples" when they look normal to us.
Imagespace is continuous: in the limit of large ε, you can perturb any image into any other—just interpolate the pixels. When we say we want an adversarially robust classifier, we mean that perturbations that change the model's output should also make a human classify the input differently. Trying to find adversarial examples against a robust image classifier amounts to trying to find the smallest change to an image that alters what it "really" looks like (to humans).
You might wonder what the smallest such change could be, or perhaps if there even is any nontrivally "smallest" change (significantly better than just interpolating between images).
Madry et al. adversarially trained a classifier for the MNIST dataset of handwritten digits. Using PGD to search for adversarial examples under the ℓ2 norm—the sum of the squares of the differences in pixel values between the original and perturbed images—the classifier's performance doesn't really tank until you crank ε up to around 4—at which point, the perturbations don't look like random noise anymore, as seen in Figure 12 from the paper:
Tasked with changing an image's class given a limited budget of how many pixels can be changed by how much, PGD concentrates its budget on human-meaningful changes—deleting part of the loop of a 9 to make a 7 or a 4, deleting the middle-left of an 8 to make a 3. In contrast to "vanilla" models whose susceptibility to adversarial examples makes us suspect their good performance on natural data is deceiving, it appears that the adversarially-trained model is seeing the same digits we are.
(I don't want to overstate the significance of this result and leave the impression that adversarial examples are necessarily "solved", but for the purposes of this post, I want to highlight the striking visual demonstration of what it looks like when adversarial training works.)[3]
An even more striking illustration of this phenomenon is provided in "Robustified ANNs Reveal Wormholes Between Human Category Percepts" by Guy Gaziv, Michael J. Lee, and James J. DiCarlo.[4]
The reason adversarial examples are surprising and disturbing is because they seem to reveal neural nets as fundamentally brittle in a way that humans aren't: we can't imagine our visual perception being so drastically effected by such small changes to an image. But what if that's just because we didn't know how to imagine the right changes?
Gaziv et al. adversarially trained image classifier models to be robust against perturbations under the ℓ2 norm of ε being 1, 3, or 10, and then tried to produce adversarial examples with ϵ up to 30.[5] (For 224×224 images in the RGB colorspace, the maximum possible ℓ2 distance is √3⋅2242≈388. The typical difference between ImageNet images is about 130.)
What they found is that adversarial examples optimized to change the robustified models' classifications also changed human judgments, as confirmed in experiments where subjects were shown the images for up to 0.8 seconds—but you can also see for yourself in the paper or on the project website. Here's Figure 3a from the paper:
The authors confirm in the Supplementary Material that random ϵ = 30 perturbations don't affect human judgments at all. (Try squinting or standing far away from the monitor to better appreciate just how similar the pictures in Figure 3a are.) The robustified models are close enough to seeing the same animals we are that adversarial attacks against them are also attacks against us, precisely targeting their limited pixel-changing budget on surprising low-ℓ2-norm "wormholes" between apparently distant human precepts.
Implications for Alignment?
Futurists have sometimes worried that our civilization's coming transition to machine intelligence may prove to be incompatible with human existence. If AI doesn't see the world the same way as we do, then there's no reason for it to steer towards world-states that we would regard as valuable. (Having a concept of the right thing is a necessary if not sufficient prerequisite for doing the right thing.)
As primitive precursors to machine intelligence have been invented, some authors have taken the capabilities of neural networks to learn complicated functions as an encouraging sign. Early discussions of AI alignment had emphasized that "leaving out just [...] one thing" could result in a catastrophic outcome—for example, a powerful agent that valued subjective experience but lacked an analogue of boredom would presumably use all its resources to tile the universe with repetitions of its most optimized experience. (The emotion of boredom is evolution's solution to the exploration–exploitation trade-off; there's no reason to implement it if you can just compute the optimal policy.)
The particular failure mode of "leaving one thing out" is starting to seem less likely on the current paradigm. Katja Grace notes that image synthesis methods have no trouble generating photorealistic human faces. Diffusion models don't "accidentally forget" that faces have nostrils, even if a human programmer trying to manually write a face image generation routine might. Similarly, large language models obey the quantity-opinion-size-age-shape-color-origin-purpose adjective order convention in English without the system designers needing to explicitly program that in or even be aware of it, despite the intuitive appeal of philosophical arguments one could make to the effect that "English is fragile." So the optimistic argument goes: if instilling human values into future AGI is as easy as specifying desired behavior for contemporary generative AI, then we might be in luck?
But even if machine learning methods make some kinds of failures due to brittle specification less likely, that doesn't imply that alignment is easy. A different way things could go wrong is if representations learned from data turn out not to be robust off the training distribution. A function that tells your AI system whether an action looks good and is right virtually all of the time on natural inputs isn't safe if you use it to drive an enormous search for unnatural (highly optimized) inputs on which it might behave very differently.
Thus, the extent to which ML methods can be made robust is potentially a key crux for views about the future of Earth-originating intelligent life. In a 2018 comment on a summary of Paul Christiano's research agenda, Eliezer Yudkowsky characterized one of his "two critical points" of disagreement with Christiano as being about how easy robust ML is:
Christiano replied, in part:
At the time in 2018, it may have been hard for readers to determine which of these views was less wrong—and maybe it's still too early to call. ("Robust ML" is an active research area, not a crisp problem statement that we can definitively say is solved or not-solved.) But it should be a relatively easier call for the ArXiv followers of 2024 than the blog readers of 2018, as the state of the art has advanced and more relevant experiments have been published. To my inexpert eyes, the Gaziv et al. "perceptual wormholes" result does seem like a clue that "ironing out the squiggles" may prove to be feasible after all—that adversarial examples are mostly explainable in terms of non-robust features and high-dimensional geometry, and remediable by better (perhaps more compute-intensive) methods—rather than being a fundamental indictment of our Society's entire paradigm for building AI.
Am I missing anything important? Probably. I can only hope that someone who isn't will let me know in the comments.
This post and much of the literature about adversarial examples focuses on image classification, in which case the input would be the pixels of an image, the output would be a class label describing the content of the image, and the loss function might be the negative logarithm of the probability that the model assigned to the correct label. But the story for other tasks and modalities is going to be much the same. ↩︎
That is, as an illustrative example, training on a dataset of birds-perturbed-to-be-classified-as-bicycles and bicycles-perturbed-to-be-classified-as-birds results in good performance on natural images of bicycles and birds. ↩︎
Madry et al. are clear that there are a lot of caveats about models trained with their methods still being vulnerable to attacks that use second-order derivatives or eschew gradients entirely—and you can see that there are still non-human-meaningful pixelly artifacts in the second row of their Figure 12. ↩︎
A version of this paper has also appeared under the less interesting title, "Strong and Precise Modulation of Human Percepts via Robustified ANNs". Do some reviewers have a prejudice against creative paper titles? While researching the present post, I was disturbed to find that the newest version of the Gilmer et al. "Adversarial Spheres" paper had been re-titled "The Relationship Between High-Dimensional Geometry and Adversarial Examples". ↩︎
Gaziv et al. use the script epsilon ε to refer to the size of perturbation used in training the robustified models, and the lunate epsilon ϵ to refer to the size used in subsequent attacks. I'm sure there's a joke here about sensitivity to small visual changes, but I didn't optimize this footnote hard enough to find it. ↩︎