Terminologically, I think it would be useful to name this as a variant of the epsilon fallacy, which has the benefit of being exactly what it sounds like.
Also, great post, I love the pasta-cooking analysis.
Another reason the pasta terminology is bad is that I bet a reasonable fraction of the population have always believed that the salt is for taste, and have never heard any other justification. For them, “salt in pasta water fallacy” would be a pretty confusing term. I like “epsilon fallacy”.
I had never heard about the salt making pasta cook faster. I know that some people only add salt when the water is on the point of boiling because this makes the boiling faster (which is also true but a negligibly tiny effect: adding salt before just increases the boiling point, meanwhile adding it when the past is already about to boil breaks surface tension and adds nucleation centres which precipitate the formation of bubbles).
Seems like it's related to the Motte-and-Bailey fallacy, where people claim more than they can defend, retreat to the defensible claim when pushed, and expand back to the indefensible claim the moment the pressure lets up.
Adding salt makes the pasta taste better. So I think this is a halo effect or manichean error - since salting the water is a good idea, it should do other good things too.
Or just a post-hoc rationalisation, by people who know you're "supposed" to salt the pasta water, but don't really know why. Because they've been taught to cook by example rather than from theory and first principles (as most of us are), maybe by someone who also didn't know why they do it.
If they've also separately heard that salt raises the boiling point of water, but don't really know the magnitude of that effect, then that presents itself as an available salient fact to slot into the empty space in "I salt my pasta water because..."
- The concrete example seems just an example of scope insensitivity?
- I don't trust the analysis of point (2) in the concrete example. It seems plausible turning off the wifi has a bunch of second-order effects, like making various wifi-connected devices not to run various computations happening when online. Consumption of the router could be smaller part of the effect. It's also quite possible this is not the case, but it's hard to say without experiments.
- I would guess most aspiring rationalists are prone to something like an "inverse salt in pasta water fallacy": doing a Fermi estimate like the one described, concluding that everyone is stupid, and stopping to add salt to pasta water.
- but actually people add salt to pasta water because of the taste
- it's plausible salt actually decreases cooking time (or increases cooking time) - but the dominant effect will be chemical interaction with the food. Salt makes some food easier to cook or harder to cook
- overall, focusing on proving something about the non-dominant effect ... is not great
the second-order effects of turning off the WiFi are surely comprised of both positive and negative effects, and i have no idea which valence it nets out to.
these days homes contain devices whose interconnectedness is used to more efficiently regulate power use. for example, the classic utility-controlled water heater, which reduces power draw when electricity is more expensive for the utility company (i.e. when peakers would need to come online). water heaters mostly don’t use WiFi but thermostats like Nest, programmable light bulbs, etc do: when you disrupt that connection, in which direction is power use more likely to change?
i have my phone programmed so that when i go to bed (put it in the “i’m sleeping” Do Not Disturb mode) it will automatically turn off all the outlets and devices — like my TV, game consoles, garage space heater — which i only use during the day. leaving any one of these on for just one night would cancel weeks of gains from disabling WiFi.
I’m actually more interested in reverse salted pasta water fallacies! It’s an extension of Chesterton’s Fence, but with an added twist where the fence has a sign with an incorrect explanation of what the fence is for.
In the language of Bayes, we might think of it thus:
E = The purpose of the fence stated on the sign H = The actual purpose of the fence is the stated one
The fallacy would simply be ascribing too high a prior value of P(H), at least within a certain reference class.
Potentially, that might be caused by rationalists tailoring their environment such that a high P(H) is a reasonable default assumption almost all the time in their lived experience. Think a bunch of SWE autistics who hang out with each other and form a culture centered on promoting literal precise statements. For them, P(H) is very high for the signs they’ll typically encounter.
The failure mode is not noticing when you’re outside the samples distribution of life circumstances - when you’re thinking about the world outside rationalist culture. It may not have a lower truth content, but it may have lower literalism. But there’s not always a clear division between them, and anyway, insisting on literalism and interrogating the false premises of mainstream culture is a way of expanding the boundaries of rationalist culture.
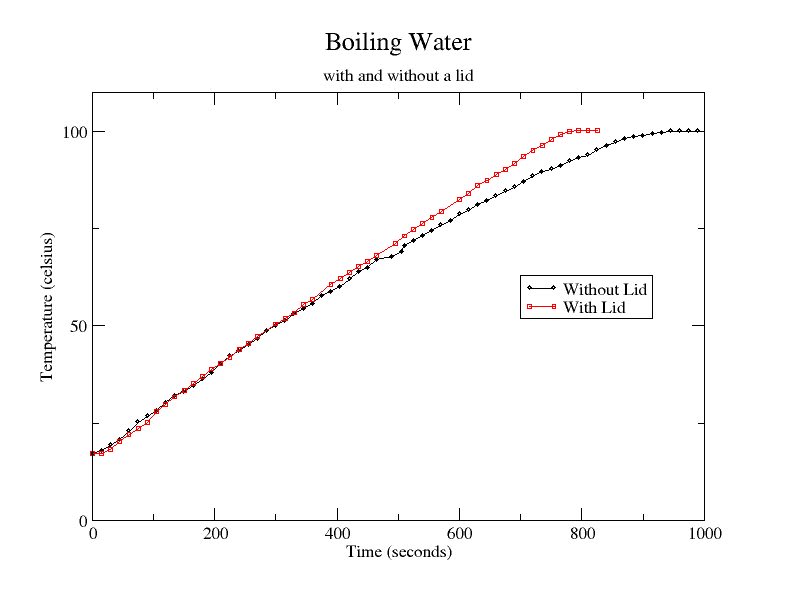
I put a lid on the pot because it saves energy/cooks faster. Or maybe it doesn't, I don't know, I never checked.
I checked and it does work.
It's the horizontal difference that matters and not the vertical one, so the water boils about 200s earlier or 20% faster (according to this one experiment) which quite nice!
Note also that there are several free parameters in this example. E.g., I just moved to Germany, and now have wimpy German burners on my stove. If I put on a large container with 6L or more of water, and I do not cover it, the water will never go beyond bubble formation into a light simmer, let alone a rolling boil. If I cover the container at this steady state, it reaches a rolling boil in about another 90s.
Also you would have to add back in additional time to get the water to its (new, higher) boiling point in the first place...
Though, actually, apparently adding salt decreases the "specific heat capacity" of water, so that increasing it by N degrees requires less heat to be added (and therefore takes less stove time). The numbers in this article suggest that this makes a larger difference than the increased boiling point would.
(Though, again, the effect size seems to be epsilon for realistic amounts of salt people would add.)
The article has an egregious typo where they say “The pot containing a 20% salt concentration will heat up over 25 times faster”. I think they meant “over 25% faster”, which is either true or close-to-true. I’m not sure about the conclusion that cooking time goes (slightly) down; I think they’re holding total-mass fixed, but if we’re talking about “adding salt” then we should hold water-mass fixed instead, which adds onto the boiling point elevation effect and might tip the balance. I didn’t do the calculation because it’s entirely pointless. :-P
Doing the math because I have the urge:
- The graphs look like straight lines within the range from 0-5% salt concentration, so I'll use the numbers at 5% and assume they scale down to the epsilon of salt one would actually add.
- Density appears to increase by 4%.
- Specific heat appears to go from 4200 to 3930 (edit: not 3850, whoops), a decrease of ~7%.
- Boiling point ... not present in your link, but this says approximately +0.5° C per 2.9% of salt, so let's say at 5% salt it becomes 100.8°C. The delta from a starting point of, say, 21°C thus increases by about 1%.
- Conclusion: time to boiling is multiplied by , a (tiny) decrease.
- Addendum: I see recommendations of 1 tablespoon of salt per gallon of water, which is 0.4% by mass, so in practice the time to boiling would be multiplied by more like 0.998.
I think you meant 3950 not 3850? And if we hold water-mass fixed instead of total-volume (i.e. the water is already in the pot and we’re deciding whether to add salt or not) we should use 5% not 4% (density doesn’t matter, because we don’t care whether the volume goes up a bit upon adding salt). Seems awfully close to even.
(I don't know much about physics, but...) Raising the boiling point just means raising the maximal temperature of the water. Since during normal (saltless) cooking that maximum is usually reached at some time x before the pasta is done, raising the boiling point with salt means the water becomes overall hotter after x, which means you have to cook (a tiny bit) shorter. What makes the pasta done is not the boiling, just the temperature of the water and the time it has some temperature.
Im pretty sure, though I cannot find data on it, that cooking in salt water simply causes salt to interact chemically with the pasta, "tenderizing" it, the same way salt tenderizes meat, vegetables etc.
I assume we could perform an experiment in which we submerge identical amounts of pasta in cold tap water, and in an equal volume of salt water, and wait until it becomes soft enough to eat. My assumption is that waterlogging pasta in salt water would soften it much faster.
Right, but if you wait for the water to boil before you put the pasta in, then you are waiting a little longer before adding the pasta. Then cooking the pasta slightly shorter after you put it in.
Yeah. And many people do indeed recommend one should add pasta only after the water is boiling. For example:
Don't add the noodles until the water has come to a rolling boil, or they'll end up getting soggy and mushy.
Except ... they don't get soggy.
I would know, I made a lot of pasta in spring of 2020!
While we're at it, they also say
Bring a large pot of water to a boil.
which other sources also tend to recommend. This is usually justified by saying that by using a lot of water the pasta will thereby stick together less. But as I said, I consider myself a noodle expert now, I optimized the process, and using a larger pot just increases the cooking time (since more water takes longer to get hot), but has no measurable influence on stickiness.
There have been multiple egregious examples of this fallacy with respect to pandemic policy. The complete lack of rational cost benefit analysis (across the political spectrum) for the various measures was truly disheartening.
But to give a less politically charged example: Locally, in response to drought conditions, some restaurants announced they would only bring glasses of water to the table, on request. Now, this might make some sense in terms of reducing labor, although the extra work of having to ask everyone, and possibly bring out additional glasses later, probably cancels this out. But for reducing water usage, this is just silly. Let's do some math:
Total water usage in US is about 1000 gal/person-day (including domestic, agricultural and industrial uses). So, assuming 50% of patrons leave their 12 oz glass of water untouched, you are reducing the daily water consumption of restaurant patrons by less than 0.005%. Of course, it also takes water to wash said glass -- it can vary a lot, but 18 oz of water would be a reasonable estimate (assuming an automatic commercial dishwater). That gets us up around 0.012%, or the water you get from running the faucet in the sink for 5-10 seconds.
The complete lack of rational cost benefit analysis (across the political spectrum) for the various measures was truly disheartening.
To be fair there also was an environment of high uncertainty in which making good CBA without data was simply impossible, and calling for extensive and unrealistic standards of proof was a common dithering technique from people who simply didn't want anything done on principle. We still lack good enough data on transmission properties to e.g. estimate properly the benefits of ventilation in reducing it, three years into this. I was honestly baffled that the first thing done in March 2020 wasn't to immediately estimate in multiple experiments how long the virus stayed in the air or on surfaces still viable, how much exposure caused infection, etc. We had like a couple of papers at best, and not very good ones, apparently because it was hard to do the experiments and they required a P4 lab or so. Meanwhile the same researchers would probably encounter the virus daily at the grocer.
It's hard to get good data, yes, particularly in a politically charged environment. But, I would have liked to have seen some evidence that for a given mitigation, our leaders tried to get a best estimate (even if it is not a great estimate) that it will prevent X COVID deaths, at a cost of Y (dollars, QALYs, whatever), and had done some reasoning why utility(X) > cost(Y). We might disagree on the values of X and Y, and how to compare them, but at least we would have a starting point for discussion. Instead, we got either "Don't take away muh freedom!" or "We must stop anyone from dying of COVID at all costs!". And a lot of people died, and we inflicted tremendous damage on ourselves, while doing some things that were maybe beneficial, and a lot of things that were clearly stupid, and we're not in a position to do better next time.
I think the problem here is also forced choices, which were in themselves loaded on purpose. If I tell you the two choices are "let COVID spread unimpeded" or "lock down without any support mechanism so that the economy crashes so hard it kills more people than COVID would" (honestly I don't think we actually fared that bad in western countries though, pre-vaccine COVID really would have killed a fuckton of people if it got in full swing), then I'm already loading the choice. Many politicians did this because essentially they were so pissy about having to do something that ran counter to their ideological inclinations that they took a particular petty pleasure in doing it as badly as they could, just to drive home that it was bad. This is standard "we believe the State is bad, that is why we will get in charge of the State and then manage it like utter fuckwits to demonstrate that the State is bad" right wing libertarian-ish behaviour. Boris Johnson and the British Tories in particular are regularly culpable of this, and were so during the pandemic as well.
A third, saner option would have been "close schools, make it legally mandated for every employer who can allow work from home to make their people work from home, implement these and those security measures for those who otherwise can't, close businesses like restaurants and cinemas temporarily, then tax (still temporarily!) the increased earnings of those citizens and companies who are less affected by these measures to pay for supporting those businesses and people that are more affected so that the former don't go bankrupt, and the latter don't starve". You know, an actual coordinated action that aims at both minimizing and spreading fairly the (inevitable) suffering that comes with being in a pandemic. Do that on and off while developing testing and tracing capacity as well as all sorts of mitigation measures, and until a vaccine is ready. Then try to phase out to a less emergency mode, more sustained regime that however still manages infection rates and their human and economic costs seriously.
We... really didn't get that. But the original sin was IMO mainly in the way pandemic plans were already laden with ideology from the get go. The whole "let it rip" thing the UK tried before desperately backtracking? That WAS our official pandemic plan. Designed for flu rather than a coronavirus with twice the R0, admittedly, but still. The best idea they could come up with was "do nothing, but pretend it's on purpose to look more clever", essentially, because everything else felt inadmissible as it impinged on this or that interest or assumption that couldn't possibly be broken. As it turns out, the one thing that plan underestimated, for all its pretences of being a masterpiece of grounded realpolitik, was the pressure from people not wanting to get sick or die. Who could have guessed. As such, the backlash and following measures like lockdowns were implemented in a rush and thus very poorly and without real plans or coordination. Might have helped to see that coming first.
The LessWrong Review runs every year to select the posts that have most stood the test of time. This post is not yet eligible for review, but will be at the end of 2024. The top fifty or so posts are featured prominently on the site throughout the year.
Hopefully, the review is better than karma at judging enduring value. If we have accurate prediction markets on the review results, maybe we can have better incentives on LessWrong today. Will this post make the top fifty?
Interesting post. As a counterpoint, a famous cycling coach in the UK spent a lot of time talking about "marginal gains". Essentially the exact opposite philosophy, chasing down all of the tiny improvements. (Random article I found on it: https://jamesclear.com/marginal-gains , although it kind of goes off course at the end into self help stuff.)
Aside, I always assumed the salt in pasta water was for some kind of osmosis thing. My vague reasoning was that water can diffuse in or out of the pasta and the concentration of non-water things (like salt or starch) on the inside vs. outside will control how much the water 'likes' one side of the barrier or not.
Something like your 3% improvement is another example of epsilon gains working.and perhaps your Realistic expectations for disagreement fit here.
This fallacy occurs when a claim is made (adding salt will reduce cooking time, turning off the wifi will save energy), that is both true, and negligible. The claim may convince one to do something (add salt, turn off the wifi), even though the advice is completely useless. This is a fallacy because the person making the claim can always argue that "The claim is true", in some logical sense, while the person receiving the advice is mislead to believe that is "The claim is relevant". It is difficult to fight the person making the claim, because they could always shift the debate toward the truth of the claim.
Why 'fight the person making the claim'?
Just saying "that's true but not relevant" seems fine enough to move on?
I think its not really related.
OP's point: "Turning off my router at night will make a positive difference, but one too miniscule to matter."
Wiki's point: "Saying that a typical household would save 27.03467 pence per year by turning off the router at night is silly. Just round to 25 or 30 pence."
There is a particular fallacy I encounter often, and I don't know if it has a name already. I call it the salt in pasta water fallacy. In this post I will present the fallacy, discuss why I believe it is a fallacy, and give a concrete example of it happening.
Salt in pasta water
The archetypical example of the fallacy is the following claim: Adding salt to pasta water reduces cooking time.
The proof for this statement can be described as follows:
"All of those points seem very reasonable", you may be wondering, "where is the fallacy?" Is there some sneaky chemistry phenomenon going on?
AFAIK no, there is none. My objection goes a bit deeper.
Let's do the math
First of all, can we estimate how big the effect is? To do this, we need to know three things:
So, now we simply multiply all of this and obtain... 2.6s. By adding salt to pasta water, one saves 2.6 seconds of cooking time.
Where is the fallacy again?
You may be wondering where I am going. The initial statement seemed true, I just added numbers, so what? Where is the fallacy.
The fallacy, I claim, is that 2.6s are nothing. Adding salt does not decrease cooking time. It doesn't increase it either, it just does nothing (wrt cooking time at least). This may seem weird to you, and I will try to detail it a bit more. The fallacy, I believe, lies in some play-on-word.
Assume for example that my friend Bob and I are in front of a cooking pot, waiting for the pasta to be ready. And Bob says "adding salt will reduce cooking time". What does this sentence mean?
I want to argue that, in this context, it has to mean (2). And, in this context, I want to claim that Bob is wrong, such a tiny reduction in cooking time doesn't justify doing anything, or even arguing about it.
Now comes the weird part. Assume that I do the math in front of Bob, and we both agree that the math is correct and it won't have an effect greater than 3s. Bob could still claim "Ok, so adding salt does reduce cooking time, you are being stubborn". Bob is now claiming he meant (1) the whole time, the proposition adding salt reduces cooking time is true. And I'd like to claim that, no, he was using meaning (2), and just backed to meaning (1) because he was wrong.
A concrete example
This winter, in France (and, I assume everywhere else in Europe), the government wanted the whole country to save energy (this had to do with the war in Ukraine and the sudden drop in Russian gas supply). A whole strategy was devised to reduce energy consumption, one aspect of it was a set of recommendations, targeted to households, and broadcast through TV, radio, and other media. I will only list the two most iconic:
(1) is a very effective idea. The government claimed that each degree would reduce the energy consumption of the whole country by 7%, which implies that each degree saves 185 TWh/year[3]. (2) is a salt in pasta water fallacy: an average wifi router consumes 6W, which means that, if the whole country (30M households) turns off the wifi 12 hours a day, this would save, over a year, 0.8 TWh[4].
But, if pushed too hard, a member of the government could always say: "even if the effect is small, it is still there, every MWh saved is a progress". To which I'd like to answer "No, you are wasting everyone's time by proposing useless solutions to a real problem".
Summary
This fallacy occurs when a claim is made (adding salt will reduce cooking time, turning off the wifi will save energy), that is both true, and negligible. The claim may convince one to do something (add salt, turn off the wifi), even though the advice is completely useless. This is a fallacy because the person making the claim can always argue that "The claim is true", in some logical sense, while the person receiving the advice is mislead to believe that is "The claim is relevant". It is difficult to fight the person making the claim, because they could always shift the debate toward the truth of the claim.
My flatmates and I lowered the temperature this winter. We do not turn off the wifi. I still put salt in the pasta water because it tastes better, and I put a lid on the pot because it saves energy/cooks faster. Or maybe it doesn't, I don't know, I never checked.
https://doi.org/10.1002/jsfa.11138, table 4
Boiling Point Rise Calculations in Sodium Salt Solutions | Industrial & Engineering Chemistry Research (acs.org)
Although this probably affects only a third of the year
On top of that, the energy from the router is not wasted, it turns into heat, thus they collectively act as electric heaters. The energy saved by turning off the routers is thus probably much smaller