There's a lot of discourse around abrupt generalization in models, most notably the "sharp left turn." Most recently, Wei et al. 2022 claim that many abilities suddenly emerge at certain model sizes. These findings are obviously relevant for alignment; models may suddenly develop the capacity for e.g. deception, situational awareness, or power-seeking, in which case we won't get warning shots or a chance to practice alignment. In contrast, prior work has also found "scaling laws" or predictable improvements in performance via scaling model size, data size, and compute, on a wide variety of domains. Such domains include transfer learning to generative modeling (on images, video, multimodal, and math) and reinforcement learning. What's with the discrepancy?
One important point is the metric that people are using to measure capabilities. In the BIG Bench paper (Figure 7b), the authors find 7 tasks that exhibit "sharp upwards turn" at a certain model size.
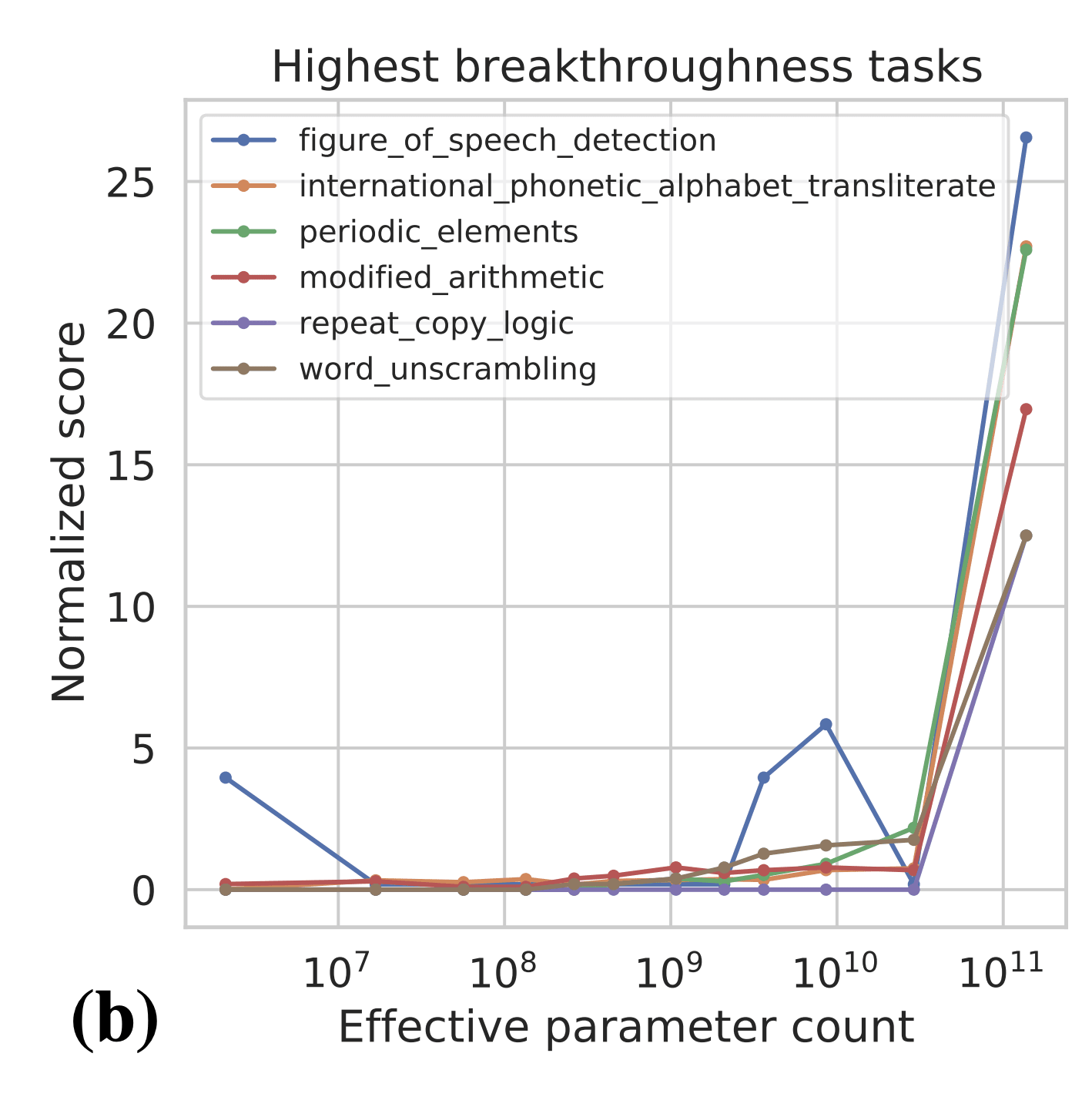
Naively, the above results are evidence for sharp left turns, and the above tasks seem like some of the best evidence we have for sharp left turns. However, the authors plot the results on the above tasks in terms of per-character log-likelihood of answer:
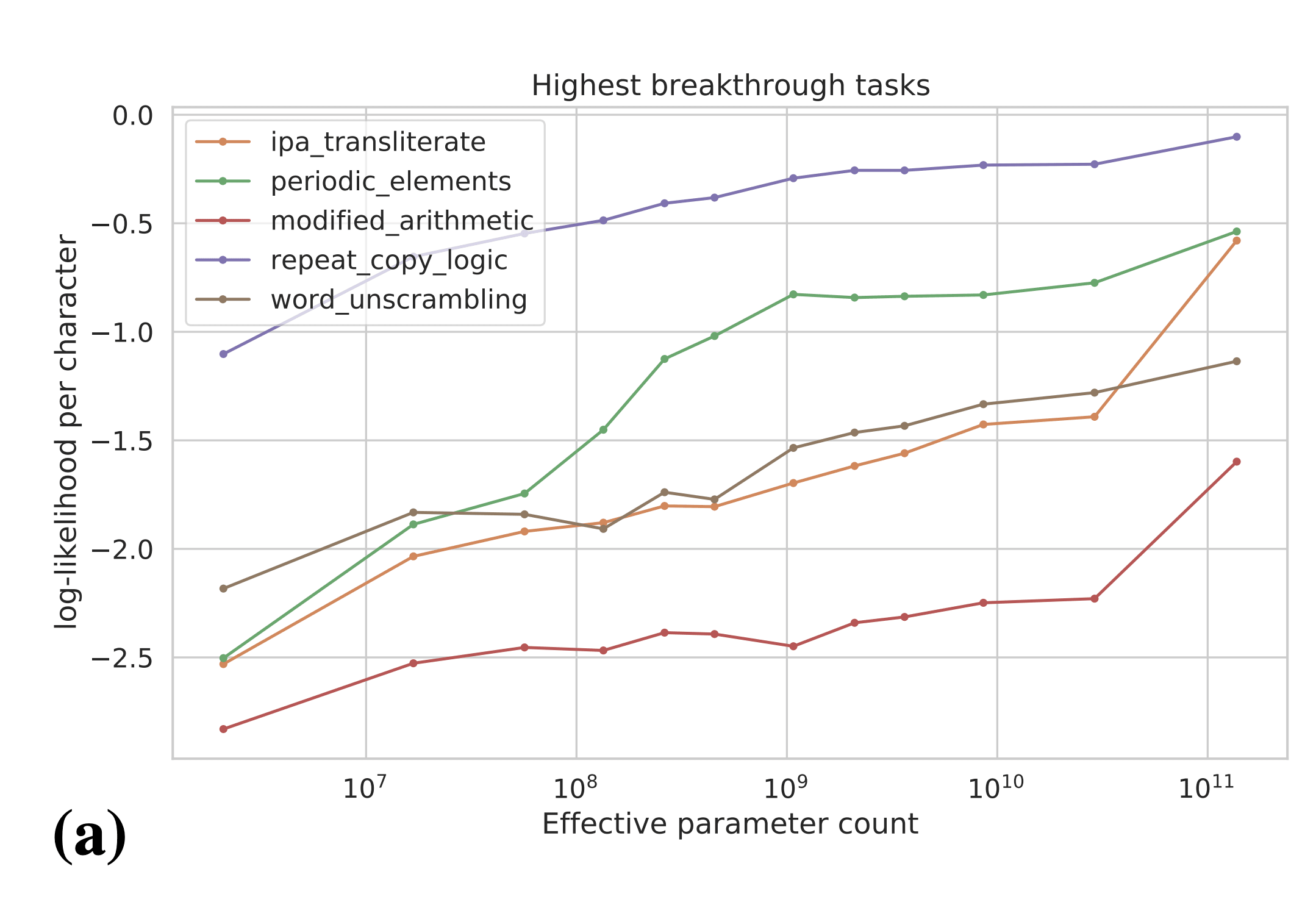
The authors actually observe smooth increases in answer log-likelihood, even for tasks which showed emergent behavior according to the natural performance metric for the task (e.g. accuracy). These results are evidence that we can predict that emergent behaviors will occur in the future before models are actually "capable" of those behaviors. In particular, these results suggest that we may be able to predict power-seeking, situational awareness, etc. in future models by evaluating those behaviors in terms of log-likelihood. We may even be able to experiment on interventions to mitigate power-seeking, situational awareness, etc. before they become real problems that show up in language model -generated text.
Clarification: I think we can predict whether or not a sharp left turn towards deception/misalignment will occur rather than exactly when. In particular, I think we should look at the direction of the trend (increases vs. decreases in log-likelihood) as signal about whether or not some scary behavior will eventually emerge. If the log likelihood of some specific scary behavior increases, that’s a bad sign and gives us some evidence it will be a problem in the future. I mainly see scaling laws here as a tool for understanding and evaluating which of the hypothesized misalignment-relevant behaviors will show up in the future. The scaling laws are useful signal for (1) convincing ML researchers to worry about scaling up further because of alignment concerns (before we see them in model behaviors/outputs) and (2) guiding alignment researchers with some empirical evidence about which alignment failures are likely/unlikely to show up after scaling at some point.
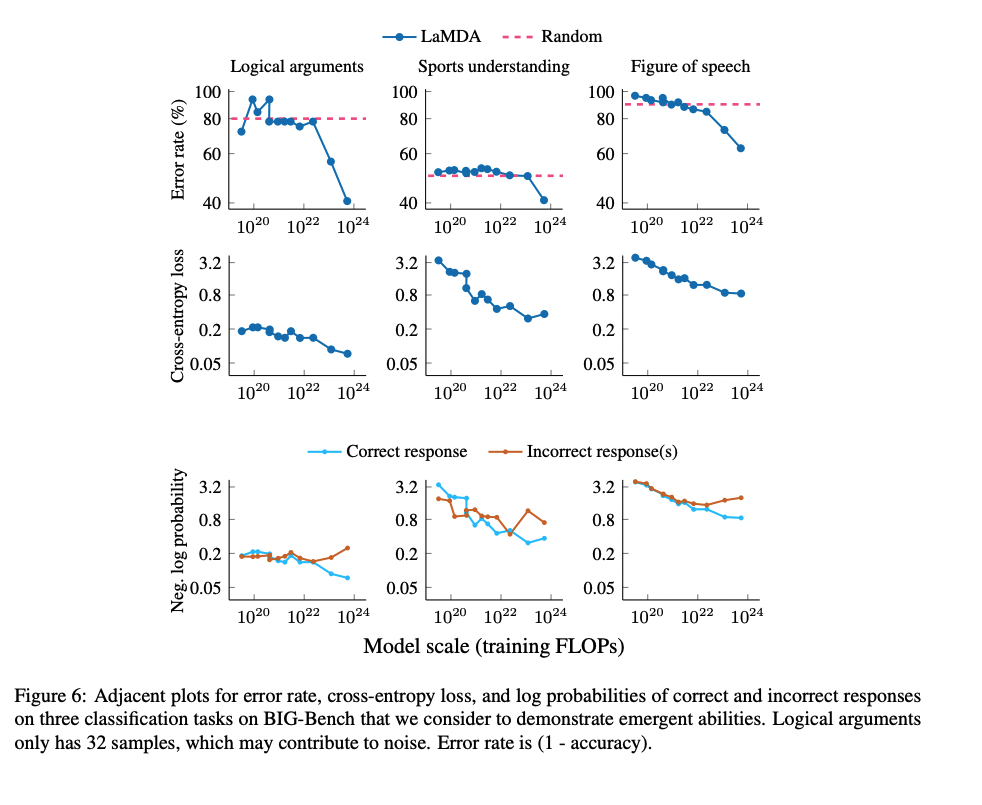
If perplexity on a task is gradually decreasing then I think that's probably produced some underlying gradual change in the model (which may be the sum of a ton of tiny discrete changes).
If accuracy and log loss are both improving, I think that's most likely due to the same underlying phenomenon. That's not nearly as obvious---it could be that there are two separate phenomena, and one gives rise to gradual improvements in perplexity without affecting accuracy while the other gives rise to abrupt improvements in accuracy without reflecting perplexity---but it still seems like a very natural guess.
The induction bump in particular seems to involve accuracy and log loss improving together, unsurprisingly.
Of course the induction behavior is just one small driver of log loss and so it corresponds to a small blip on the loss or accuracy curves overall, while corresponding to a big jump on some subtasks. In a larger model there are likely to be many events like this that don't correspond to any blip at all in the overall loss curve while being important for a subtask. This seems unlikely to be the driver of the difference for the BIG bench tasks under discussion, since the continuous log probability improvements and discontinuous accuracy improvements are being measured on the same distribution.
In the case of parities, I think there is a smooth underlying change in the model, e.g. see figure 3 in this paper. I agree that (i) such changes are not always visible in perplexity, e.g. for parities, and therefore it's not obvious that you will know where to look for them even if they exist, (ii) it's not obvious whether they always exist, we just know about a few cases we've studied like parities and grokking.