There's a lot of discourse around abrupt generalization in models, most notably the "sharp left turn." Most recently, Wei et al. 2022 claim that many abilities suddenly emerge at certain model sizes. These findings are obviously relevant for alignment; models may suddenly develop the capacity for e.g. deception, situational awareness, or power-seeking, in which case we won't get warning shots or a chance to practice alignment. In contrast, prior work has also found "scaling laws" or predictable improvements in performance via scaling model size, data size, and compute, on a wide variety of domains. Such domains include transfer learning to generative modeling (on images, video, multimodal, and math) and reinforcement learning. What's with the discrepancy?
One important point is the metric that people are using to measure capabilities. In the BIG Bench paper (Figure 7b), the authors find 7 tasks that exhibit "sharp upwards turn" at a certain model size.
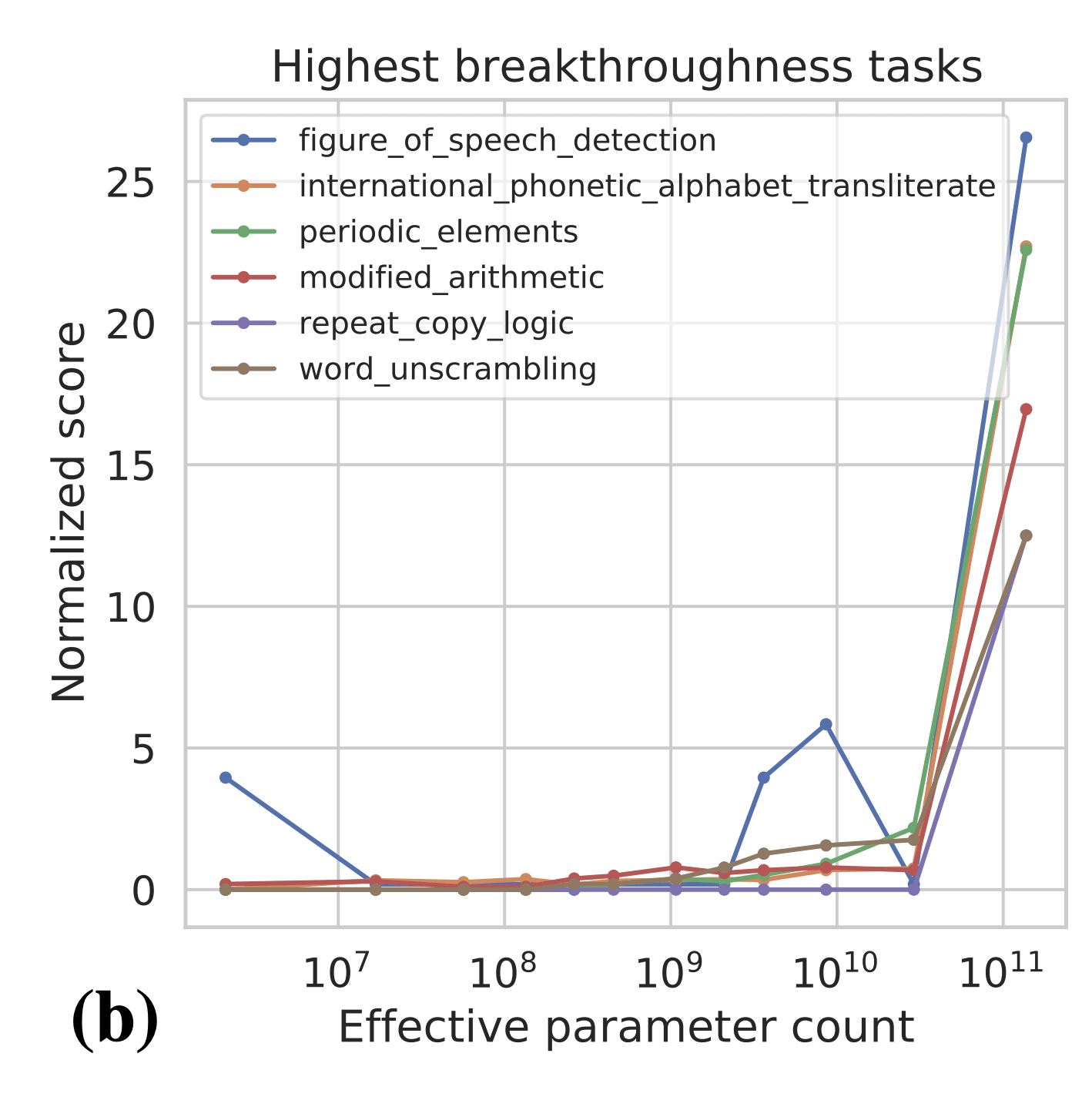
Naively, the above results are evidence for sharp left turns, and the above tasks seem like some of the best evidence we have for sharp left turns. However, the authors plot the results on the above tasks in terms of per-character log-likelihood of answer:
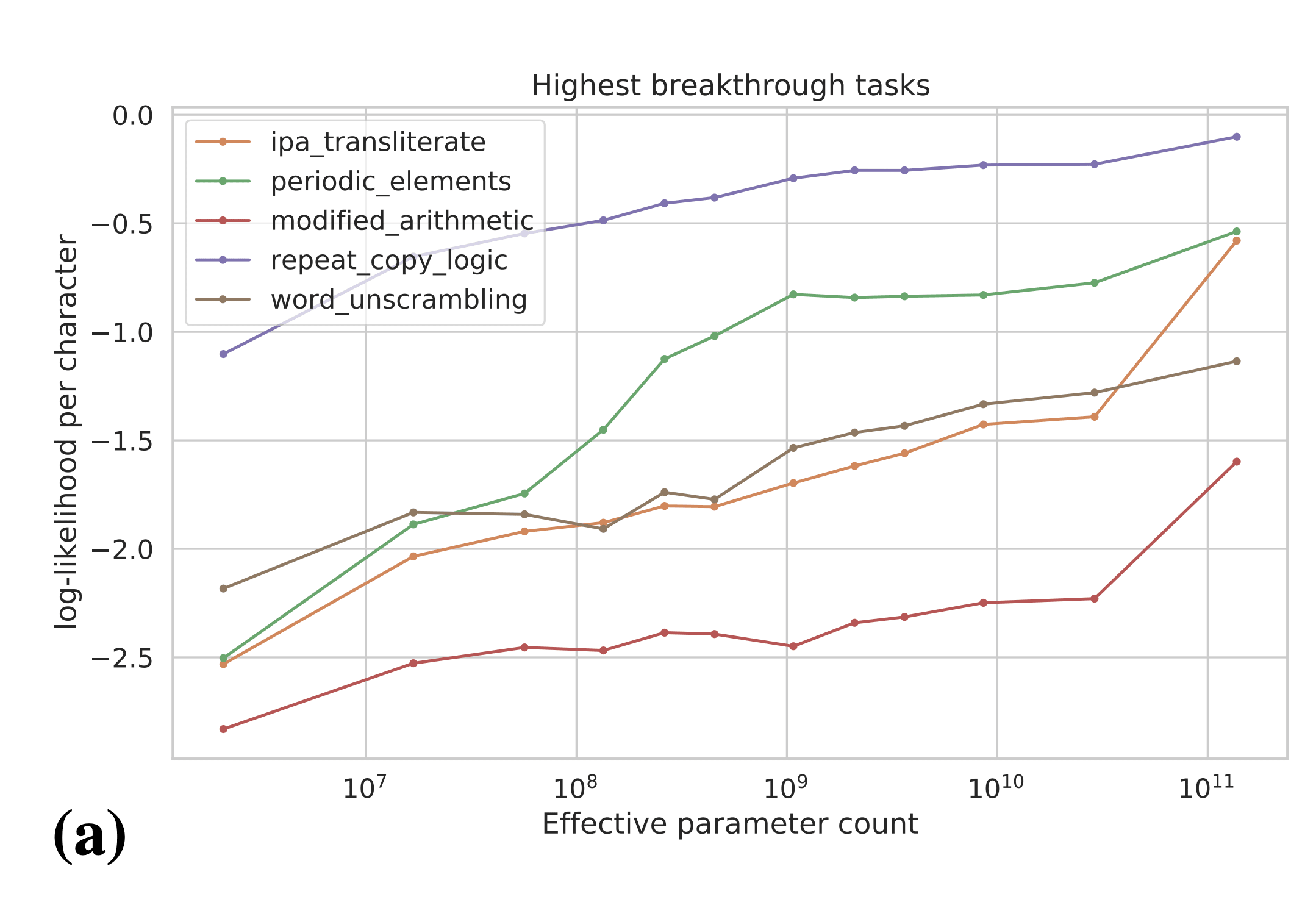
The authors actually observe smooth increases in answer log-likelihood, even for tasks which showed emergent behavior according to the natural performance metric for the task (e.g. accuracy). These results are evidence that we can predict that emergent behaviors will occur in the future before models are actually "capable" of those behaviors. In particular, these results suggest that we may be able to predict power-seeking, situational awareness, etc. in future models by evaluating those behaviors in terms of log-likelihood. We may even be able to experiment on interventions to mitigate power-seeking, situational awareness, etc. before they become real problems that show up in language model -generated text.
Clarification: I think we can predict whether or not a sharp left turn towards deception/misalignment will occur rather than exactly when. In particular, I think we should look at the direction of the trend (increases vs. decreases in log-likelihood) as signal about whether or not some scary behavior will eventually emerge. If the log likelihood of some specific scary behavior increases, that’s a bad sign and gives us some evidence it will be a problem in the future. I mainly see scaling laws here as a tool for understanding and evaluating which of the hypothesized misalignment-relevant behaviors will show up in the future. The scaling laws are useful signal for (1) convincing ML researchers to worry about scaling up further because of alignment concerns (before we see them in model behaviors/outputs) and (2) guiding alignment researchers with some empirical evidence about which alignment failures are likely/unlikely to show up after scaling at some point.
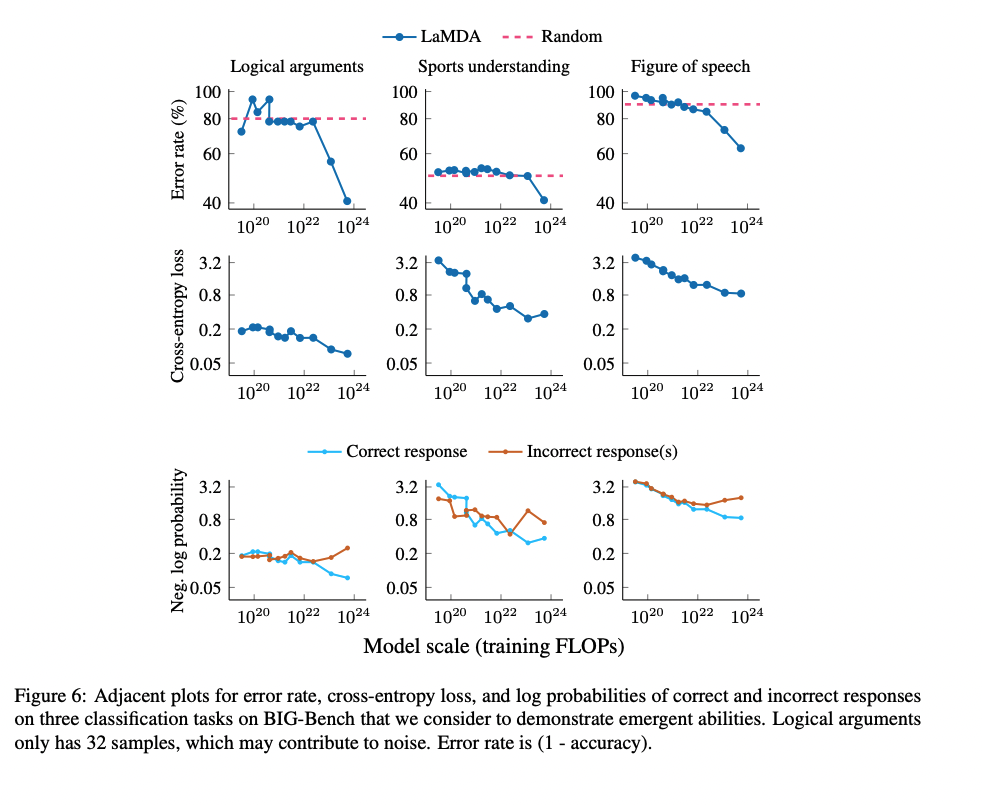
The picture of phase changes from your post, as well as the theoretical analysis here, both suggest that you may be able to observe capabilities as they form if you know what to look for. It seems like a kind of similar situation to the one suggested in the OP, though I think with a different underlying mechanism (in the OP I think there probably is no similar phase change in the model itself for any of these tasks) and a different set of things to measure.
In general if we get taken by surprise by a capability, it seems fairly likely that the story in retrospect would be that we just didn't know what to measure. So for people worried about rapid emergence it seems natural to try to get really good at predicting these kinds of abrupt changes, whether they are coming from phase changes in the model, non-convexities from RL exploration (which exhibit hyperbolic phase changes), or performance measurements that elide progress.
(My guess would be that deception is significantly smoother than any of the trends discussed here, which are themselves significantly smoother than bona fide phase changes, just because larger and larger combinations tend to get smoother and smoother. But it still seems possible to get taken by surprise especially if you aren't being very careful.)