There's a lot of discourse around abrupt generalization in models, most notably the "sharp left turn." Most recently, Wei et al. 2022 claim that many abilities suddenly emerge at certain model sizes. These findings are obviously relevant for alignment; models may suddenly develop the capacity for e.g. deception, situational awareness, or power-seeking, in which case we won't get warning shots or a chance to practice alignment. In contrast, prior work has also found "scaling laws" or predictable improvements in performance via scaling model size, data size, and compute, on a wide variety of domains. Such domains include transfer learning to generative modeling (on images, video, multimodal, and math) and reinforcement learning. What's with the discrepancy?
One important point is the metric that people are using to measure capabilities. In the BIG Bench paper (Figure 7b), the authors find 7 tasks that exhibit "sharp upwards turn" at a certain model size.
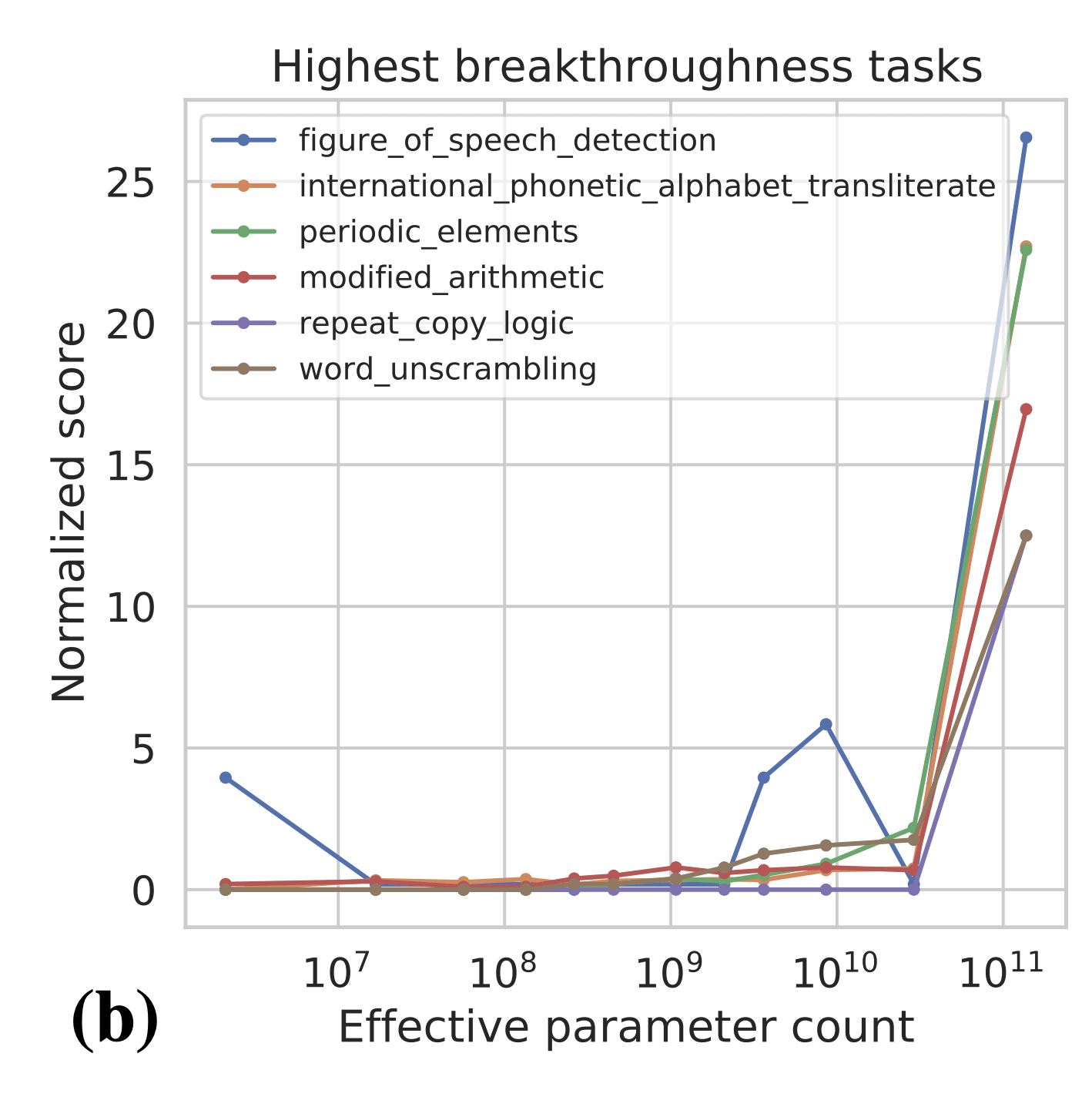
Naively, the above results are evidence for sharp left turns, and the above tasks seem like some of the best evidence we have for sharp left turns. However, the authors plot the results on the above tasks in terms of per-character log-likelihood of answer:
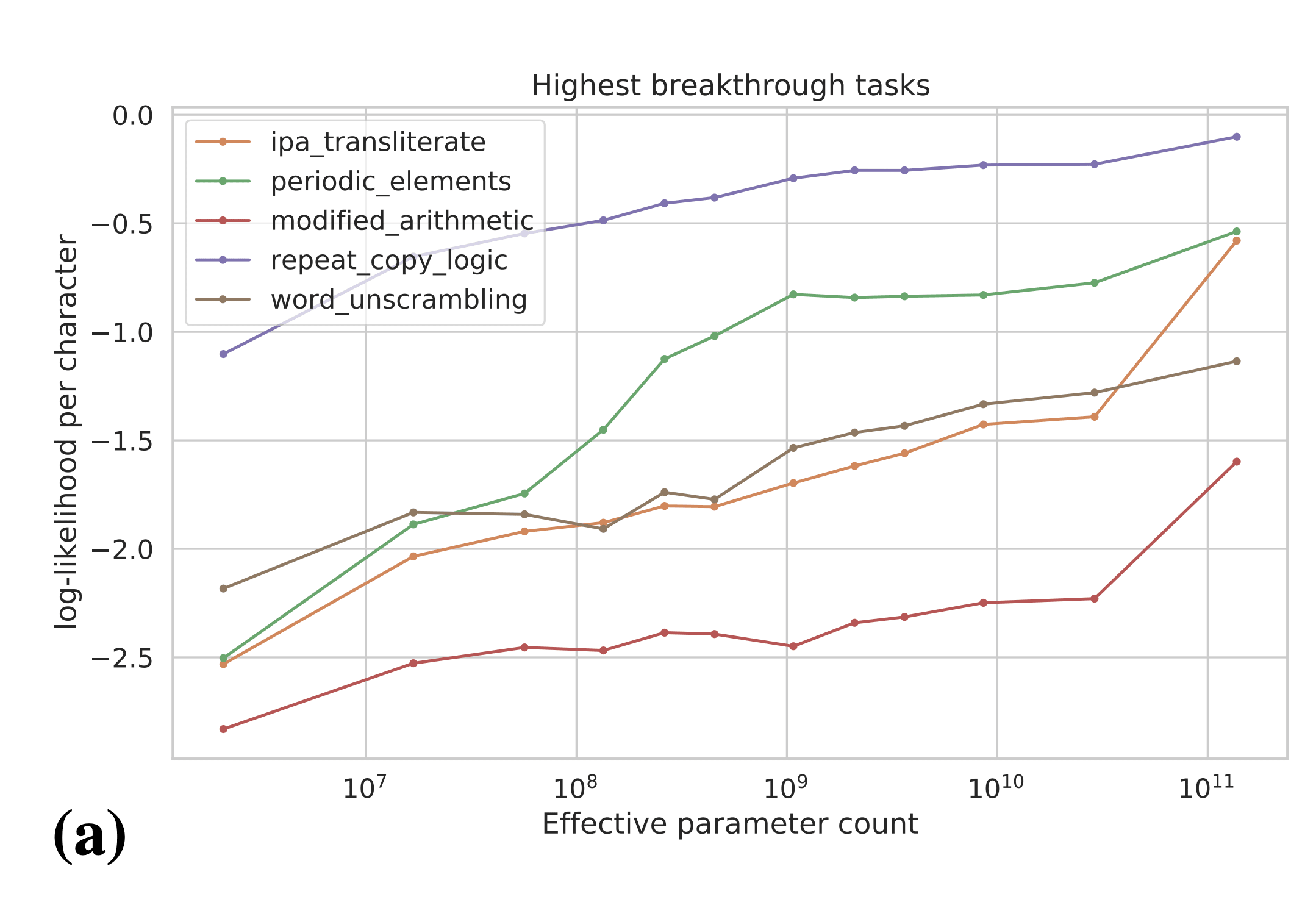
The authors actually observe smooth increases in answer log-likelihood, even for tasks which showed emergent behavior according to the natural performance metric for the task (e.g. accuracy). These results are evidence that we can predict that emergent behaviors will occur in the future before models are actually "capable" of those behaviors. In particular, these results suggest that we may be able to predict power-seeking, situational awareness, etc. in future models by evaluating those behaviors in terms of log-likelihood. We may even be able to experiment on interventions to mitigate power-seeking, situational awareness, etc. before they become real problems that show up in language model -generated text.
Clarification: I think we can predict whether or not a sharp left turn towards deception/misalignment will occur rather than exactly when. In particular, I think we should look at the direction of the trend (increases vs. decreases in log-likelihood) as signal about whether or not some scary behavior will eventually emerge. If the log likelihood of some specific scary behavior increases, that’s a bad sign and gives us some evidence it will be a problem in the future. I mainly see scaling laws here as a tool for understanding and evaluating which of the hypothesized misalignment-relevant behaviors will show up in the future. The scaling laws are useful signal for (1) convincing ML researchers to worry about scaling up further because of alignment concerns (before we see them in model behaviors/outputs) and (2) guiding alignment researchers with some empirical evidence about which alignment failures are likely/unlikely to show up after scaling at some point.
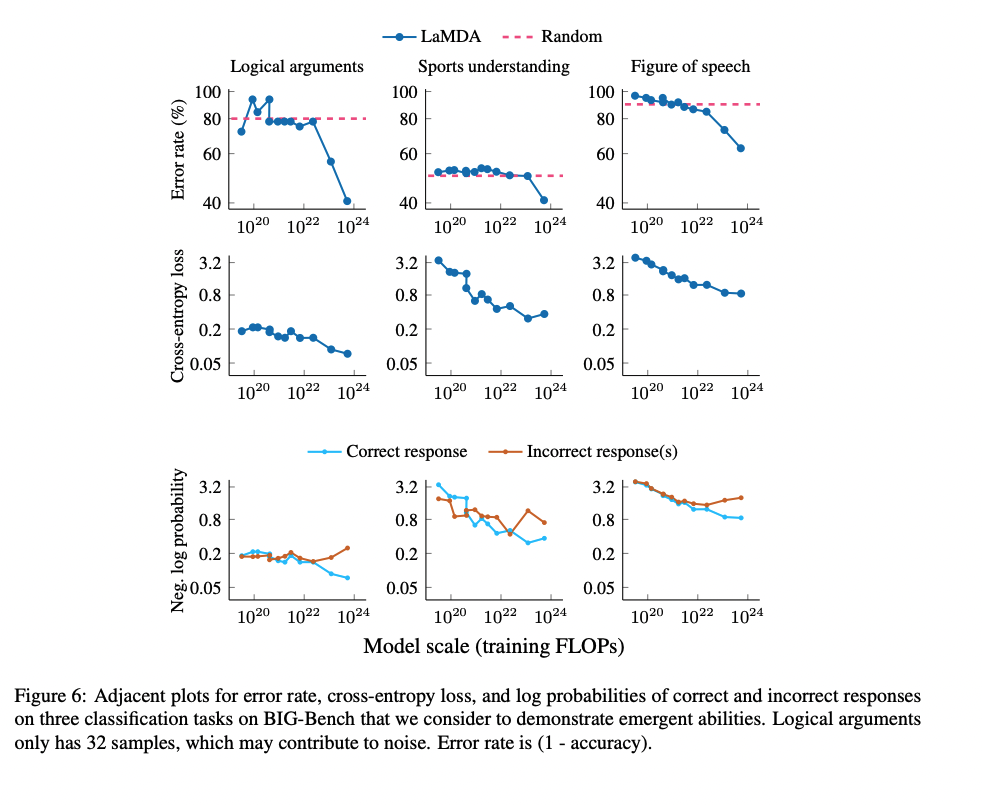
That does not seem true to me and as much of a leap as OP. A priori, if I see a smooth curve in one metric and a discontinuous or abrupt change in another, I do not see how that should make me more confident that it is 'about behavior or evaluation'. Why should I conclude that? Why can't it reflect a non-smooth underlying change in the model first? I would only conclude that if I had already ruled out internal changes because I was already committed to the position that NNs can only learn and change internally in smooth small ways... which unfortunately we already know is a false position, because of things like Anthropic's induction bump, which show phase transitions in the internals of the model which is nearly invisible on the loss. (And also, incidentally, because the bump is so small and the training curve still so smooth, falsifies the more modest claim that small changes in perplexity must reflect small changes in the model internals - maybe usually small changes do not reflect non-smooth underlying changes, but nevertheless, it is entirely possible and does happen, and we would surely find many more routine examples if we had better interpretability so examining a single instance didn't take man-years.) And also a priori, from the old statistical mechanics literature, you should expect abrupt phase changes of various sorts in NN models (which may or may not be visible in the training curve), like parity models, where the task is so simple and clearly defined that it cannot have anything to do with the 'behavior' or 'evaluation' being wrong, and comes from effects like symmetry-breaking (often associated with plateaus and flat curves...).