I was reading a post on the economy from the political statistics blog FiveThirtyEight, and the following graph shocked me:
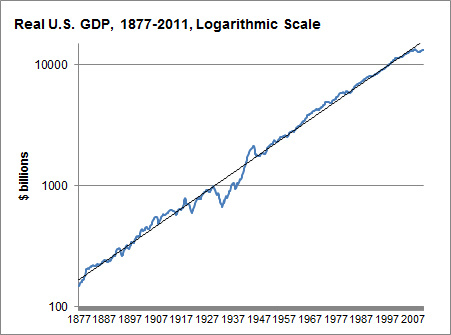
This, according to Nate Silver, is a log-scaled graph of the GDP of the United States since the Civil War, adjusted for inflation. What amazes me is how nearly perfect the linear approximation is (representing exponential growth of approximately 3.5% per year), despite all the technological and geopolitical changes of the past 134 years. (The Great Depression knocks it off pace, but WWII and the postwar recovery set it neatly back on track.) I would have expected a much more meandering rate of growth.
It reminds me of Moore's Law, which would be amazing enough as a predicted exponential lower bound of technological advance, but is staggering as an actual approximation:
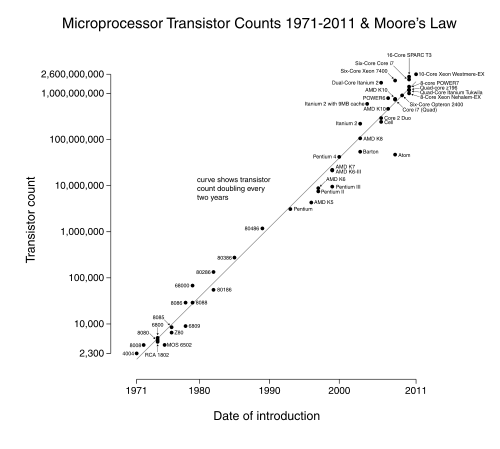
I don't want to sound like Kurzweil here, but something demands explanation: is there a good reason why processes like these, with so many changing exogenous variables, seem to keep right on a particular pace of exponential growth, as opposed to wandering between phases with different exponents?
EDIT: As I commented below, not all graphs of exponentially growing quantities exhibit this phenomenon- there still seems to be something rather special about these two graphs.

Any time the current growth rate depends linearly on the size of the current population, you get exponential growth.
For instance, given effectively boundless food, the number of bacteria will double every regular time period because, in that time period, each bacterium can split into more.
Similarly, human populations grow exponentially (up to environmental bounds like food supply, war, etc.) because after roughly twenty years, humans beget more humans. With a population as gargantuan as Earth's, that growth rate is practically continuous.
Kurzweil's argument is that this applies to many technological industries, too. Faster, more powerful computers make it easier and faster to design the next technological generation. Thus when you measure computing power with any one well-defined scale like transistor count, you'll find that the growth rate depends on the current number. Ergo, exponential.
I'm not sure what's going on with the GDP, but if it's really keeping so nicely to an exponential curve like that, then I'd expect it means that the growth in GDP depends primarily on the current GDP and that it has been this way for a very long time.
I don't know whether this is what's really going on. As others here have pointed out, there might be some biases playing a role here. And as I suspect has been beaten to death here before, Kurzweil hides a number of dubious assumptions about market forces and human creativity in his projections. But I do know that if you really, honestly have a strongly exponential growth pattern, it's most likely that you'll find some reason why the growth rate depends on the current population.
US population, 1790-2000.
US GNP per capita, 1875-2010.
Could there be an economic-technocratic explanation of the steadiness of growth since 1950? That is, did someone decide that annual GNP growth should be 3.5% (which is 2% growth per capita, according to Kehoe's graph), and has policy been determined accordingly?